Книга: Апология математики (сборник статей)
Назад: 4. Можно ли аксиоматически определить понятие натурального ряда (со строчной буквы)?
Дальше: 6. Что такое доказательство?
5. «Можно ли доказать, что великую теорему ферма нельзя ни доказать, ни опровергнуть?»
Именно так было озаглавлено пятое размышление в опубликованном в 1987 г. первоначальном тексте этой работы. В то время убеждение в справедливости Великой теоремы Ферма основывалось на некой иррациональной вере: доказательство теоремы отсутствовало, отсутствовало и опровержение. Напомним, что опровержение какого-либо утверждения состоит в доказательстве его ложности; опровергнуть утверждение – значит доказать, что оно является ложным, иначе говоря, доказать его отрицание.
Однако с тех пор в мировой науке произошло важное событие: более чем через 350 лет после того, как была сформулирована Великая теорема Ферма, она была наконец доказана! Автором доказательства стал сорокалетний англичанин Эндрю Уайлс (A. Wiles), выпускник аспирантуры Кембриджа, переехавший в 1980-е гг. в Америку и ставший профессором Принстонского университета.
Доказательство Уайлса рождалось с драматизмом, достойным Великой теоремы. После многих лет упорной работы к маю 1993 г. Уайлс был убеждён, что обладает доказательством, которое он изложил в общих чертах в трёх лекциях, прочитанных в его родном Кембридже 21–23 июня 1993 г. В номере от 5 июля 1993 г. известный американский журнал Time посвятил этому событию статью с подзаголовком «Решена самая знаменитая математическая проблема в истории». В январе 1994 г. популярный математический журнал опубликовал статью [31] о многовековой осаде Великой теоремы Ферма – осаде, завершившейся предпринятым Уайлсом семилетним штурмом; впрочем, в конце статьи содержалось следующее примечание:
На декабрь 1993 г. рукопись Уайлса ещё не обнародована. Кен Райбет (Ken Ribet) отмечает, что применительно к длинным рукописям подобная задержка является сравнительно нормальной. Большинство экспертов продолжает верить в то, что в основном доказательство правильно.
Однако, когда Уайлс записал своё доказательство, в нём обнаружился пробел (т. е. недоказанный логический переход). Над учёным нависла угроза провала. (Здесь уместно вспомнить судьбу Георга Кантора.) К счастью, в сентябре 1994 г. с помощью своего ученика Ричарда Тэйлора (R. Taylor) Уайлс сумел пробел устранить. Уточнённое доказательство Уайлса теперь уже не подвергается сомнению в мире математиков. Подробнее обо всём этом можно прочесть в замечательной книге Саймона Сингха [32].
Итак, теорема Ферма доказана. Поэтому избранный нами в качестве заголовка вопрос «Можно ли доказать, что Великую теорему Ферма нельзя ни доказать, ни опровергнуть?» потерял свой смысл и потому взят в кавычки; сегодня ответом на него должно служить уверенное «нельзя». Попробуем, однако, перенестись в прошлое, когда теорема Ферма ещё не была ни доказана, ни опровергнута. Будем рассуждать в рамках того прошедшего времени, когда ещё не было известно, появится ли когда-либо доказательство или опровержение Великой теоремы. С современной точки зрения настоящее, пятое, размышление, вероятно, следовало бы озаглавить так: «Можно ли когда-либо было ожидать (опасаться, надеяться) получить доказательство того, что Великую теорему Ферма нельзя ни доказать, ни опровергнуть?» Мы увидим, что ожидать этого было никак нельзя.
Проблема континуума, упомянутая в конце нашего предыдущего размышления, относится к числу главных проблем, волновавших умы математиков. В знаменитом докладе «Математические проблемы», с которым великий Гильберт выступил в 1900 г. на Международном конгрессе в Париже, она была названа первой. Как было отмечено, проблема континуума оказалась неразрешимой: континуум-гипотезу невозможно ни доказать, ни опровергнуть. Перечисляя 23 основные проблемы математики, Гильберт не упомянул проблему доказательства (или опровержения) Великой теоремы Ферма. По-видимому, Гильберт не считал эту проблему достаточно важной. Тем не менее нет сомнения, что это самая знаменитая из не решённых в то время математических проблем. И притом единственная из таких проблем, известных, к сожалению, широкой массе нематематиков. Мы написали «к сожалению», ибо ощутимую долю времени математики-профессионалы тратят на изучение и опровержение сочинений ферматистов – так называются люди, не имеющие должной математической подготовки, но считающие, что они доказали теорему Ферма.
Если считать, что под теоремами следует понимать лишь те математические утверждения, истинность которых установлена путём доказательства, то теорему Ферма нельзя называть теоремой, а следует называть гипотезой Ферма. Ведь доказательство «теоремы Ферма» ещё не найдено. Но если обозначать словом «теорема» математическое утверждение, истинность которого подлежит установлению путём доказательства, то термин «теорема Ферма» оказывается законным. Как бы то ни было, мы будем употреблять именно его. (Не чуждого терминологических проблем читателя приглашаем взглянуть на статьи «Теорема» и «Ферма теорема» в «Математической энциклопедии» [22, 23].)
Много факторов способствовало популярности теоремы Ферма в среде непрофессионалов. Среди них: 1) авторитетность автора (теорему сформулировал великий французский математик Пьер де Ферма); 2) почтенность возраста (она была высказана около 1630 г.); 3) романтические обстоятельства, при которых она была сформулирована (Ферма записал её на полях латинского перевода «Арифметики» Диофанта издания 1621 г. Восьмая задача второй книги «Арифметики» Диофанта гласит: «Заданный квадрат разложить на два квадрата». Ферма сделал к этой задаче следующее замечание (также на латыни): «Наоборот, невозможно разложить ни куб на два куба, ни биквадрат на два биквадрата – вообще никакую степень, бóльшую квадрата, на две степени с тем же показателем. Я открыл этому поистине чудесное доказательство, но эти поля для него слишком узки». В бумагах Ферма доказательства найдено не было.); 4) учреждение в 1908 г. премии Вольфскеля в 100 тысяч германских марок за доказательство теоремы Ферма («приятный» факт учреждения большой премии, естественно, получил гораздо бóльшую известность, чем «неприятный» факт её обесценивания вследствие наступившей после Первой мировой войны инфляции); 5) простота формулировки.
Конечно, первые четыре фактора не смогли бы сработать, не будь теорема Ферма столь общедоступна по своей формулировке. Вот в чём она состоит: каково бы ни было целое число n, большее чем 2, уравнение хп + уп = zn не имеет целых положительных решений.
Как видим, участвующее в формулировке теоремы Ферма уравнение рассматривают как уравнение с тремя неизвестными: х, у, z. Поскольку п может принимать значения 3, 4, 5, 6 и т. д., то на самом деле речь идёт о бесконечной серии уравнений и утверждается, что ни одно из них не имеет решения в таких целых х, у, z, что х > 0, у > 0, z > 0. С логической точки зрения более естественно рассматривать уравнение хn + уn = zn как одно уравнение с четырьмя неизвестными п, х, у, z. Теорема Ферма, стало быть, утверждает, что это уравнение не имеет целых решений, таких что п > 2, х > 0, у > 0, z > 0.
Современные эксперты сходятся во мнении, что Ферма на самом деле не обладал доказательством своей теоремы, хотя, возможно, умел её доказывать для двух частных случаев, а именно: для случая, когда показатель степени п равен 3, и для случая, когда этот показатель равен 4. Впервые доказательства для этих двух случаев были опубликованы великим швейцарским и российским математиком Эйлером в XVIII в. Заметим, что из доказательства теоремы Ферма для какого-либо показателя n немедленно вытекает её доказательство для всех показателей, делящихся на n. Таким образом, ещё в XVIII в. теорема была доказана для всех показателей, делящихся на 3 или на 4. Далее теорема Ферма была доказана последовательно для показателей, делящихся на 5 (1825 г.), на 14 (1832 г.), на 7 (1839 г.). К 1978 г. справедливость теоремы Ферма была установлена для всех показателей, меньших 125 000. Однако все эти успехи не позволяют утверждать истинность теоремы Ферма в её полном объёме, т. е. утверждать отсутствие таких положительных целых чисел х, у, z, которые смогли бы удовлетворить уравнению хn + уn = zn хотя бы при одном каком-нибудь показателе п, большем чем 2.
Попытки доказать теорему Ферма продолжаются. Теоретически могли бы предприниматься и попытки её опровержения, но этого не происходит. Ситуация с гипотезой, называемой «теоремой Ферма», значительно отличается от той, которая имеет место для континуум-гипотезы, ведь, как мы знаем, доказано, что континуум-гипотезу нельзя ни доказать, ни опровергнуть (точнее, Гёдель в 1939 г. показал, что её нельзя опровергнуть, а Коэн в 1963 г. – что её нельзя доказать). Для гипотезы (теоремы) Ферма такое доказательство – доказательство того, что её невозможно ни доказать, ни опровергнуть – отсутствует. Спрашивается, доказательство пока отсутствует (и остаётся надежда получить его в будущем) или это в принципе невозможно? Если бы такое доказательство удалось получить, это, несомненно, принесло бы математике большую пользу, поскольку раз и навсегда закрыло бы шлюз для потока безграмотных попыток доказать теорему Ферма.
К сожалению, такое доказательство невозможно. И мы сейчас разъясним, почему невозможно. Правда, остаётся теоретическая возможность того, что удастся доказать, что теорему Ферма нельзя доказать. Появление такого доказательства также перекрыло бы вышеназванный шлюз, но тогда, вероятно, возник бы поток попыток опровергнуть теорему Ферма (например, путём предъявления в косвенной форме четвёрок астрономически больших чисел п, х, у, z, для которых нужное равенство было бы практически непроверяемым).
Итак, предположим:
(а) существует доказательство того, что теорему Ферма нельзя доказать;
(б) существует доказательство того, что теорему Ферма нельзя опровергнуть.
Наша цель теперь – показать, что (а) и (б) несовместимы, т. е. не может быть, чтобы оба эти утверждения были истинны одновременно. На самом же деле мы обнаружим, что (б) несовместимо даже с более слабым, чем (а), утверждением (a1): теорему Ферма нельзя доказать. А именно, мы покажем, что из (б) следует: теорема Ферма поддается доказательству, что исключает (a1).
Начнём с некоторых предварительных комментариев. Всякую четвёрку натуральных чисел п, х, у, z, такую, что n > 2, x > 0, у > 0, z > 0 и хn + уn = zn, условимся называть четвёркой Ферма. Теорема Ферма гласит, что четвёрок Ферма не существует в природе. Опровергнуть какую-либо теорему – это значит доказать истинность противоположного. Опровергнуть теорему Ферма – значит доказать, что четвёрки Ферма существуют.
Лемма 1. Если нельзя доказать, что четвёрки Ферма существуют, то их не существует.Замечание. Пусть А – какое-либо утверждение. Нет никаких причин считать, что если нельзя доказать, что А верно, то А неверно. Однако – и в этом содержание леммы – это так, коль скоро А есть утверждение «четвёрки Ферма существуют».Доказательство. Поведём доказательство от противного. В самом деле, предположим, что четвёрки Ферма существуют. Выпишем какую-либо из них. Это будет четвёрка натуральных чисел a, b, с, d. Проверим, что это действительно четвёрка Ферма, т. е. проверим, выполняются ли неравенства a > 2, b > 0, с > 0, d > 0 и равенство bа + са = dа. Предъявление четвёрки a > 2, b > 0, с > 0, d > 0 вкупе с указанной проверкой образует доказательство существования четвёрки Ферма. Разумеется, если четвёрка состоит из гигантских чисел, то время, потребное на проверку, может превосходить длительность жизни человека, а то и всего человечества (а объём вычислений – размеры видимой Вселенной). Однако мы от этого отвлекаемся и считаем, что даже и в этом случае проверка того, что предъявленная четвёрка является четвёркой Ферма, возможна в принципе. Философ скажет, что здесь мы используем так называемую абстракцию потенциальной осуществимости, как раз и состоящую в отвлечении от ограниченности наших реальных возможностей в пространстве и времени.Лемма 2. Если нельзя опровергнуть теорему Ферма, то теорема Ферма верна.Замечание. Не видно причин, почему это должно быть верно для любой теоремы.Доказательство. Лемма 2 есть просто переформулированная лемма 1. Ведь «опровергнуть теорему Ферма» – значит «доказать, что четвёрки Ферма существуют», а «теорема Ферма верна» – значит «четвёрки Ферма не существуют».
Лемма 2, которую мы доказали, имеет строение «если Р, то Q». Поэтому если Р имеет доказательство, то и Q имеет доказательство (доказательство Q состоит в сочетании доказательства леммы с доказательством Р). Поэтому имеем сформулированное ниже следствие леммы 2.
Следствие леммы 2. Если существует доказательство того, что нельзя опровергнуть теорему Ферма, то существует и доказательство того, что теорема Ферма верна, т. е. попросту доказательство теоремы Ферма.
Ввиду важности этого следствия ещё раз сформулируем его: если существует доказательство того, что теорему Ферма нельзя опровергнуть, то теорему Ферма можно доказать. Итак, если верно (б), то теорему Ферма можно доказать, что и представляет собою обещанное отрицание утверждения (a1).
Полученное противоречие и завершает наше рассуждение о том, что (a1) и (б), а тем более (а) и (б), несовместимы.
Возникает следующий естественный вопрос: а почему проведённое рассуждение нельзя повторить для континуум-гипотезы, о которой шла речь в конце нашего предыдущего, четвёртого, размышления? В самом деле, гипотеза (теорема) Ферма утверждает, что нет четвёрок Ферма, а континуум-гипотеза – что нет множеств мощности, промежуточной между 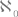 и
и 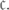 Давайте заменим четвёрку Ферма на множество промежуточной мощности, теорему Ферма – на континуум-гипотезу и повторим только что проведённое рассуждение. Мы должны, обязаны где-то споткнуться, ведь утверждения (а') и (б'), получаемые из (а) и (б) заменой слов «теорема Ферма» на слово «континуум-гипотеза», оба верны. Где же мы споткнёмся? А вот где: в доказательстве леммы 1 (разумеется, не в первоначальной формулировке, а в той, где слова «четвёрки Ферма» заменены словами «множества промежуточной мощности»). Приведённое выше доказательство леммы 1 основывалось на следующей идее: можно фактически предъявить четвёрку чисел а, b, с, d и удостовериться, что она образует четвёрку Ферма. Но что значит «предъявить множество»? Могут возразить, что и мы, собственно, предъявляем не числа как количественные категории – их предъявить невозможно, можно только написать их имена (например, в виде ноля со штрихами или в виде десятичной записи). Но дело в том, что каждое натуральное число имеет имя, чего нельзя сказать о множествах: множеств больше, чем имён (если понимать последние как конечные комбинации знаков какого-нибудь алфавита). Но даже если ограничиться множествами, имеющими имена, и предъявлять вместо множеств эти имена, всё равно остаётся главная трудность: как проверить, что предъявленное множество имеет промежуточную мощность? Проверить, что четвёрка чисел есть четвёрка Ферма, в принципе (если отвлечься от количества шагов и необходимого пространства), несложно: надо подставить числа в уравнение и сравнить левую и правую части. Способа же, который позволил бы по предъявленному множеству определить его мощность или хотя бы определить, будет ли эта мощность удовлетворять неравенству
Давайте заменим четвёрку Ферма на множество промежуточной мощности, теорему Ферма – на континуум-гипотезу и повторим только что проведённое рассуждение. Мы должны, обязаны где-то споткнуться, ведь утверждения (а') и (б'), получаемые из (а) и (б) заменой слов «теорема Ферма» на слово «континуум-гипотеза», оба верны. Где же мы споткнёмся? А вот где: в доказательстве леммы 1 (разумеется, не в первоначальной формулировке, а в той, где слова «четвёрки Ферма» заменены словами «множества промежуточной мощности»). Приведённое выше доказательство леммы 1 основывалось на следующей идее: можно фактически предъявить четвёрку чисел а, b, с, d и удостовериться, что она образует четвёрку Ферма. Но что значит «предъявить множество»? Могут возразить, что и мы, собственно, предъявляем не числа как количественные категории – их предъявить невозможно, можно только написать их имена (например, в виде ноля со штрихами или в виде десятичной записи). Но дело в том, что каждое натуральное число имеет имя, чего нельзя сказать о множествах: множеств больше, чем имён (если понимать последние как конечные комбинации знаков какого-нибудь алфавита). Но даже если ограничиться множествами, имеющими имена, и предъявлять вместо множеств эти имена, всё равно остаётся главная трудность: как проверить, что предъявленное множество имеет промежуточную мощность? Проверить, что четвёрка чисел есть четвёрка Ферма, в принципе (если отвлечься от количества шагов и необходимого пространства), несложно: надо подставить числа в уравнение и сравнить левую и правую части. Способа же, который позволил бы по предъявленному множеству определить его мощность или хотя бы определить, будет ли эта мощность удовлетворять неравенству  не существует.
не существует.
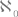 и
и 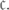 Давайте заменим четвёрку Ферма на множество промежуточной мощности, теорему Ферма – на континуум-гипотезу и повторим только что проведённое рассуждение. Мы должны, обязаны где-то споткнуться, ведь утверждения (а') и (б'), получаемые из (а) и (б) заменой слов «теорема Ферма» на слово «континуум-гипотеза», оба верны. Где же мы споткнёмся? А вот где: в доказательстве леммы 1 (разумеется, не в первоначальной формулировке, а в той, где слова «четвёрки Ферма» заменены словами «множества промежуточной мощности»). Приведённое выше доказательство леммы 1 основывалось на следующей идее: можно фактически предъявить четвёрку чисел а, b, с, d и удостовериться, что она образует четвёрку Ферма. Но что значит «предъявить множество»? Могут возразить, что и мы, собственно, предъявляем не числа как количественные категории – их предъявить невозможно, можно только написать их имена (например, в виде ноля со штрихами или в виде десятичной записи). Но дело в том, что каждое натуральное число имеет имя, чего нельзя сказать о множествах: множеств больше, чем имён (если понимать последние как конечные комбинации знаков какого-нибудь алфавита). Но даже если ограничиться множествами, имеющими имена, и предъявлять вместо множеств эти имена, всё равно остаётся главная трудность: как проверить, что предъявленное множество имеет промежуточную мощность? Проверить, что четвёрка чисел есть четвёрка Ферма, в принципе (если отвлечься от количества шагов и необходимого пространства), несложно: надо подставить числа в уравнение и сравнить левую и правую части. Способа же, который позволил бы по предъявленному множеству определить его мощность или хотя бы определить, будет ли эта мощность удовлетворять неравенству
Давайте заменим четвёрку Ферма на множество промежуточной мощности, теорему Ферма – на континуум-гипотезу и повторим только что проведённое рассуждение. Мы должны, обязаны где-то споткнуться, ведь утверждения (а') и (б'), получаемые из (а) и (б) заменой слов «теорема Ферма» на слово «континуум-гипотеза», оба верны. Где же мы споткнёмся? А вот где: в доказательстве леммы 1 (разумеется, не в первоначальной формулировке, а в той, где слова «четвёрки Ферма» заменены словами «множества промежуточной мощности»). Приведённое выше доказательство леммы 1 основывалось на следующей идее: можно фактически предъявить четвёрку чисел а, b, с, d и удостовериться, что она образует четвёрку Ферма. Но что значит «предъявить множество»? Могут возразить, что и мы, собственно, предъявляем не числа как количественные категории – их предъявить невозможно, можно только написать их имена (например, в виде ноля со штрихами или в виде десятичной записи). Но дело в том, что каждое натуральное число имеет имя, чего нельзя сказать о множествах: множеств больше, чем имён (если понимать последние как конечные комбинации знаков какого-нибудь алфавита). Но даже если ограничиться множествами, имеющими имена, и предъявлять вместо множеств эти имена, всё равно остаётся главная трудность: как проверить, что предъявленное множество имеет промежуточную мощность? Проверить, что четвёрка чисел есть четвёрка Ферма, в принципе (если отвлечься от количества шагов и необходимого пространства), несложно: надо подставить числа в уравнение и сравнить левую и правую части. Способа же, который позволил бы по предъявленному множеству определить его мощность или хотя бы определить, будет ли эта мощность удовлетворять неравенству  не существует.
не существует.замечание. Можно указать на ещё одно философское различие между ситуацией с теоремой Ферма и ситуацией с континуум-гипотезой. Обсуждая вопрос о возможных доказательствах теоремы Ферма или её возможных опровержениях (т. е. доказательствах её отрицания), мы исходили из понятия доказательства в общем, неформальном смысле; об этом понятии – наше шестое размышление. Упоминавшиеся же открытия Гёделя, установившего, что континуум-гипотезу нельзя опровергнуть, и Коэна, установившего, что континуум-гипотезу нельзя доказать, утверждают невозможность формальных доказательств в рамках некоторого ранее известного конкретного представления о формальном доказательстве – более точно, в рамках некоторой конкретной аксиоматики теории множеств, а именно так называемой системы Цермело – Френкеля. Однако считается (мнение это представляет собой не что иное, как акт веры), что система Цермело – Френкеля позволяет формализовать любое неформальное математическое доказательство. Это и даёт право говорить, что континуум-гипотезу нельзя ни доказать, ни опровергнуть какими бы то ни было средствами, допускаемыми современной математикой.
Обсуждаемая тема имеет самое тесное отношение к знаменитой теореме Гёделя о неполноте. Теорема эта утверждает, что, какое бы ни было предложено понятие формального доказательства, имеется такое утверждение о натуральных числах, что ни оно само, ни его отрицание не обладает формальным доказательством в рамках предложенного понятия. Мы исходим из очевидности того, что возможны различные определения формального доказательства. Эти определения отличаются друг от друга набором допускаемых аксиом и правил вывода. Могут быть такие представления о формальном доказательстве, в котором вообще не используются ни аксиомы, ни правила вывода. Короче говоря, подходы к понятию формального доказательства могут быть весьма различны. Но все эти подходы имеют и фундаментальную общность, выражаемую в следующих принципах:
1. Каждое формальное доказательство есть текст, т. е. конечная цепочка знаков, выбранных из некоторого алфавита;
2. Каждый текст, составленный из букв рассматриваемого алфавита, поддается алгоритмической проверке на предмет того, является ли он формальным доказательством или нет, и если да, то какого именно утверждения;
3. Только истинные утверждения могут обладать формальными доказательствами.
В силу третьего принципа предъявление формального доказательства какого-либо утверждения гарантирует его истинность и, следовательно, может считаться его доказательством. Обратное, конечно, не предполагается: не предполагается, что каждое истинное или даже содержательно доказуемое утверждение имеет – при заранее заданном понятии формального доказательства – формальное доказательство. Анализ теоремы Гёделя о неполноте показывает, что утверждение, о котором в ней идёт речь, всегда имеет вид  – некоторое свойство натурального числа х. Это свойство зависит от рассматриваемого понятия формального доказательства, но всегда алгоритмически проверяемо (подобно тому, как алгоритмически проверяемо свойство четвёрки чисел «быть четвёркой Ферма»). Итак, теорема Гёделя утверждает, что
– некоторое свойство натурального числа х. Это свойство зависит от рассматриваемого понятия формального доказательства, но всегда алгоритмически проверяемо (подобно тому, как алгоритмически проверяемо свойство четвёрки чисел «быть четвёркой Ферма»). Итак, теорема Гёделя утверждает, что  не имеют формального доказательства.
не имеют формального доказательства.
 – некоторое свойство натурального числа х. Это свойство зависит от рассматриваемого понятия формального доказательства, но всегда алгоритмически проверяемо (подобно тому, как алгоритмически проверяемо свойство четвёрки чисел «быть четвёркой Ферма»). Итак, теорема Гёделя утверждает, что
– некоторое свойство натурального числа х. Это свойство зависит от рассматриваемого понятия формального доказательства, но всегда алгоритмически проверяемо (подобно тому, как алгоритмически проверяемо свойство четвёрки чисел «быть четвёркой Ферма»). Итак, теорема Гёделя утверждает, что  не имеют формального доказательства.
не имеют формального доказательства.Ужесточим наши требования к представлениям о формальном доказательстве. А именно потребуем, чтобы выполнялось следующее условие: коль скоро для какого-то алгоритмически проверяемого свойства 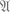 утверждение
утверждение 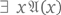 оказывается истинным, то это утверждение
оказывается истинным, то это утверждение 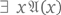 обладает формальным доказательством. Это требование довольно естественно; оно реализуется при формализации следующих уже встречавшихся выше этапов: 1) предъявления некоторого с; 2) проверки, что это с удовлетворяет свойству
обладает формальным доказательством. Это требование довольно естественно; оно реализуется при формализации следующих уже встречавшихся выше этапов: 1) предъявления некоторого с; 2) проверки, что это с удовлетворяет свойству 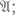 здесь существенно и то, что с можно фактически предъявить, и то, что
здесь существенно и то, что с можно фактически предъявить, и то, что 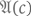 можно фактически проверить.
можно фактически проверить.
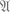 утверждение
утверждение 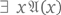 оказывается истинным, то это утверждение
оказывается истинным, то это утверждение 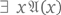 обладает формальным доказательством. Это требование довольно естественно; оно реализуется при формализации следующих уже встречавшихся выше этапов: 1) предъявления некоторого с; 2) проверки, что это с удовлетворяет свойству
обладает формальным доказательством. Это требование довольно естественно; оно реализуется при формализации следующих уже встречавшихся выше этапов: 1) предъявления некоторого с; 2) проверки, что это с удовлетворяет свойству 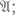 здесь существенно и то, что с можно фактически предъявить, и то, что
здесь существенно и то, что с можно фактически предъявить, и то, что 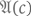 можно фактически проверить.
можно фактически проверить.Наше требование вытекает, в частности, из следующих двух ещё более естественных требований:
1) если для числа с справедливо (алгоритмически) проверяемое свойство  то
то 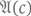 обладает формальным доказательством;
обладает формальным доказательством;
 то
то 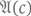 обладает формальным доказательством;
обладает формальным доказательством;2) для какого угодно свойства  если для некоторого с утверждение
если для некоторого с утверждение 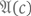 обладает формальным доказательством, то и
обладает формальным доказательством, то и 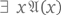 обладает формальным доказательством.
обладает формальным доказательством.
 если для некоторого с утверждение
если для некоторого с утверждение 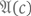 обладает формальным доказательством, то и
обладает формальным доказательством, то и 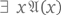 обладает формальным доказательством.
обладает формальным доказательством.Теперь, прибегнув к рассуждениям, аналогичным тем, которые применялись в связи с теоремой Ферма, приходим к следующему выводу: если ни утверждение  ни его отрицание
ни его отрицание  не обладают формальным доказательством, то одно это уже позволяет заключить, которое из этих двух утверждений верно, а именно: верно
не обладают формальным доказательством, то одно это уже позволяет заключить, которое из этих двух утверждений верно, а именно: верно 
 ни его отрицание
ни его отрицание  не обладают формальным доказательством, то одно это уже позволяет заключить, которое из этих двух утверждений верно, а именно: верно
не обладают формальным доказательством, то одно это уже позволяет заключить, которое из этих двух утверждений верно, а именно: верно 
В самом деле, если бы было верно  то это утверждение обладало бы формальным доказательством; стало быть,
то это утверждение обладало бы формальным доказательством; стало быть, 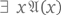 неверно, а
неверно, а  верно.
верно.
 то это утверждение обладало бы формальным доказательством; стало быть,
то это утверждение обладало бы формальным доказательством; стало быть, 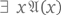 неверно, а
неверно, а  верно.
верно.Давайте ещё раз оценим парадоксальность ситуации: из одного только факта, что ни А, ни не-А не обладают формальным доказательством, можно заключить, которое из этих двух высказываний истинно на самом деле.
Назад: 4. Можно ли аксиоматически определить понятие натурального ряда (со строчной буквы)?
Дальше: 6. Что такое доказательство?

