6. Что такое доказательство?

Книга: Апология математики (сборник статей)

Назад: 5. «Можно ли доказать, что великую теорему ферма нельзя ни доказать, ни опровергнуть?»

Дальше: 7. Можно ли сделать математику понятной?

Если мы читаем книгу, написанную 50 лет назад, то рассуждения, которые мы в ней находим, кажутся нам большей частью лишёнными логической строгости.

анри пуанкаре. наука и метод. 1908 [2, с. 356]

В предыдущем размышлении встречался как термин «доказательство», так и термин «формальное доказательство». Иногда считают, что формальное доказательство – это такое доказательство, которое формально. Мы предпочитаем смотреть на эти понятия иначе.

Формальное доказательство – это математический объект, подобный, скажем, матрице или треугольнику. Это конечная цепочка знаков некоторого заранее фиксированного алфавита, т. е., как говорят в математике, слово в этом алфавите. Говоря «знак», мы не имеем в виду – в данном случае – какую-либо смысловую, содержательную сторону, но только внешнюю, графическую. Чтобы подчеркнуть это обстоятельство, в математике, когда имеют в виду внешнюю, графическую сторону, говорят не «знак», а «буква». К числу букв относят обычно буквы алфавитов реальных языков (русского, латинского и т. д.), цифры, знаки препинания. Разумно отнести к числу букв и пробел между словами (словами в обычном, не математическом смысле), изобретая для его обозначения какой-либо специальный символ, например #. Это даёт возможность рассматривать текст, т. е. последовательность слов, как слово (в уточнённом выше математическом смысле). Итак, формальное доказательство – это прежде всего слово в некотором алфавите, алфавите формальных доказательств. Разумеется, этим ни в малейшей степени не исчерпывается понятие формального доказательства; мы просто хотели подчеркнуть, что понятие формального доказательства относится к разряду слов, так же как понятие треугольника – к разряду геометрических фигур.

Какие именно слова следует считать формальными доказательствами – это тема особого разговора, выходящего за круг предметов, которые мы хотели бы здесь обсудить. Подчеркнём, что можно дать различные определения понятию формального доказательства, каждое из которых приводит к своему множеству формальных доказательств. Некоторые общие положения, которым должно подчиняться любое разумное определение, были изложены в предыдущем размышлении. Заметим, впрочем, что иногда делают ещё один шаг в сторону общности и не требуют заранее, чтобы формальными доказательствами обладали только истинные утверждения, полностью отделяя понятие формального доказательства от понятия истины. А затем это отброшенное требование вводят в виде дополнительного свойства (которым формальные доказательства, вообще говоря, могут и не обладать), а именно: множество формальных доказательств называют семантически непротиворечивым, если всякое утверждение, обладающее формальным доказательством, истинно. Более точно общие представления о формальных доказательствах излагаются с помощью понятия дедуктики (см., например, [21]).

Подчеркнём ещё, что формальными доказательствами могут обладать (или не обладать) не сами содержательно понимаемые утверждения, а лишь их записи (т. е. опять-таки слова) в каком-либо точно заданном логико-математическом языке.

Определение понятия формального доказательства – быть может, лучше сказать «определение множества формальных доказательств» – в широких пределах (обусловленных указанными выше общими ограничительными свойствами множества формальных доказательств) произвольно. Здесь имеется в виду тот «юридический» произвол, который отличает математические определения вообще. Мы имеем «юридическое» право, например, произвольно определить класс функций и назвать их «как хотим», например непрерывными.

Другое дело, что всякое разумное математическое определение обычно претендует на то, чтобы соответствовать некоторым интуитивным представлениям, отражать их. Законность определения ещё не означает его разумности. Так, математическое понятие непрерывной кривой отражает (с той или иной точностью) наши интуитивные, содержательные представления о траектории движущейся точки. Аналогично понятие формального доказательства отражает интуитивные представления о содержательном доказательстве.

Можно сказать, что понятие формального доказательства является математической моделью понятия доказательства – в том же смысле, в каком понятие непрерывной кривой является математической моделью понятия траектории.

Остаётся выяснить, что же такое доказательство – не формальное доказательство, а просто доказательство. Хотя, как мы отмечаем в самом начале настоящего очерка, неправильно полагать, что в математике всё доказывается, нет сомнений, что понятие доказательства играет в математике центральную роль. «Со времён греков говорить "математика" – значит говорить "доказательство"» – так начинает свои «Начала математики» Николя Бурбаки [6, с. 231]. Вместе с тем мы отмечали, что понятие доказательства не принадлежит математике (математике принадлежит лишь его математическая модель – формальное доказательство). Оно принадлежит логике, лингвистике и больше всего – психологии.

Итак, термин «доказательство» – один из самых главных в математике – не имеет точного определения. А приблизительное его определение таково: доказательство – это убедительное рассуждение, убеждающее нас настолько, что с его помощью мы способны убеждать других [12, с. 8]. Пожалуй, всё-таки следует уточнить, что под словом «нас» в этом определении понимаются те, кто слушает или читает доказательство, а не те, кто его воспроизводит, т. е. произносит или пишет.

Восприняв доказательство, мы делаемся в известной степени агрессивными, готовыми убеждать других с помощью этого воспринятого нами рассуждения. Если же мы не готовы, значит, мы ещё не восприняли предъявленного нам рассуждения как доказательства, а если и признали его доказательством, то просто чтобы отмахнуться.

Заметим, что понятия, присутствующие в нашем определении доказательства, – либо логико-лингвистические («рассуждение»), либо психологические («убеждающее», «способны убеждать»). Это полностью отвечает сути дела: само представление о доказательстве неразрывно связано с языковыми средствами и с социальной психологией человека. И то и другое изменяется с ходом истории. Меняется языковое оформление доказательств. Меняется и представление об убедительности.

Представление об убедительности зависит не только от эпохи, но и от социальной среды. К сожалению, я не могу сейчас вспомнить, где читал пассаж на следующую тему. Кардиналы, современники Галилея, были неглупые люди, некоторые из них могли воочию наблюдать горы на Луне в Галилеев телескоп, а также с пониманием следить за логикой рассуждений Галилея. Однако для них их собственные взгляды, основанные на априорной догме, были убедительнее любого эксперимента и любой логики. (Интересный анализ того, как априорно суженное представление о способах доказывания препятствует признанию некоторых фактов, приведён в статье С. П. Божича [13].)

Представление об убедительности того или иного рассуждения зависит от многих факторов. Выявление этих факторов – важная задача логики и психологии. В число таких факторов входит, например, разделение понятий (а точнее, терминов) на осмысленные и бессмысленные. Понятия флогистона и теплорода, считавшиеся осмысленными в XVIII в., признаются сейчас бессмысленными. Эйнштейн открыл, что бессмысленным является и понятие одновременности двух событий – если считать его объективным, не зависящим от наблюдателя (более точно, Эйнштейн открыл, что одновременность не двуместное отношение между двумя событиями, а трёхместное отношение, членами которого являются 1-е событие, 2-е событие и наблюдатель). С другой стороны, такое «очевидно бессмысленное понятие», как бесконечно малое число, вот уже полвека наполняется точным смыслом в рамках так называемого нестандартного анализа. С изменением представлений об осмысленности или бессмысленности понятий меняется и представление о самой сущности научной истины. Меняется представление об очевидности. Как в своё время все знали, что гроза вызывается высшими силами, так теперь все знают, что причина грозы – атмосферное электричество. Неспособность инертных газов образовывать химические соединения была настолько очевидной, что это свойство закрепили в самом названии «инертные». Когда же в 1962 г. были получены первые соединения, которые эти газы образуют с другими веществами, химики, по-видимому, не испытали никакого стыда, а лишь с удовольствием констатировали, что «для объяснения строения этих соединений не потребовалось принципиально новых представлений о природе химической связи» (Большая Советская Энциклопедия, 3-е изд., статья «Инертные газы»).

То, что человеческое знание меняется с ходом истории, разумеется, общее место. Здесь хотелось бы подчеркнуть, что в состав знания входят не только сами факты, но и исходные предпосылки, презумпции, на основании которых тот или иной факт делается членом системы знаний: представления об осмысленности и бессмысленности, об очевидности и неочевидности, о возможном и невозможном, о частном и общем, об убедительности и неубедительности, о доказанном и недоказанном, о достоверном и недостоверном. Все эти представления, хотя, возможно, и меняются медленнее простых представлений о фактах, в сущности, так же исторически относительны, как и последние.

Математика иногда воспринимается как скала, неподвижно возвышающаяся над волнами переменчивых представлений, относящихся к другим наукам. Конечно, основания для такого взгляда на математику имеются. Тем не менее взгляд на математику как на нечто абсолютное, видимо, являет собой преувеличение. Если математика и абсолютна, то только на уровне повседневного опыта – точно так же, как абсолютна ньютоновская физика в применении к явлениям «средних масштабов» (а в очень малом и в очень большом действует уже иная, эйнштейновская физика).

В частности, социально-историческая обусловленность представлений о «доказательствах вообще» распространяется и на математические доказательства.

Для иллюстрации сказанного автор сейчас попытается изложить вкратце свои представления о понятии доказательства в Древнем Египте, в Древней Греции и в Индии.

У нас не так много достоверных сведений о том, как излагались и воспринимались математические доказательства в древности. Многие из дошедших до нас текстов весьма отрывочны; к тому же встречающиеся в них термины зачастую допускают различную интерпретацию. Многое приходится домысливать. Каждый домысливает в желательную для себя сторону, и автор этих строк, надо думать, не исключение. С учётом этих оговорок можно составить следующую схему.

Представление о доказательстве есть продукт социальной истории общества. Мы отдаём себе отчёт в упрощённости наших исторических подходов, приписывая Древнему Египту централизованную государственность, хотя и там были периоды раздробленности, а Древней Греции – демократию, хотя и там случались тиранические правления. Но любая схема предполагает упрощения.

Итак, Древний Египет. Теократическое государство с необычайно сильной центральной властью. В качестве действенного инструмента поддержания централизации, повиновения, порядка выступает постоянное строительство пирамид, требующее колоссальных людских и материальных ресурсов и объединяющее усилия всей страны. Авторитет фараона и жрецов непререкаем. Непререкаем и авторитет написанного слова. Если что-то сказал или написал жрец, писец, учитель, значит, это есть истина. Если что-то написано на папирусе, это есть истина. Убедительность основывается на авторитетности источника.

Математические тексты Древнего Египта содержат готовые правила без какого бы то ни было их обоснования. Говоря об отсутствии обоснования, мы имеем здесь в виду современное понимание слова «обоснование». С точки зрения древнего египтянина, написанное на папирусе было полностью обосновано тем, что исходило из авторитетного источника и было запечатлено в авторитетной форме записи на папирусе. Факт занесения на папирус, запечатления на нём и был сам по себе доказательством. Действительно, этого было достаточно для того, чтобы с его помощью убеждать других. Ряд правил для вычисления площадей треугольников и четырёхугольников не получил в наши дни однозначного толкования; идут споры, как надо понимать входящие в них термины [4, глава IV, § 2, а]. В зависимости от толкования эти формулы должны восприниматься либо как точные, либо как приближённые, либо как вообще неверные. Говоря о неверной формуле, мы имеем в виду выражение площади треугольника через полупроизведение основания на боковую сторону. Многие исследователи считают, впрочем, что соответствующий древнеегипетский термин надо трактовать не как боковую сторону, а как высоту (и тогда формула из папируса оказывается верной). Однако, даже если бы этот термин означал в действительности не высоту, а боковую сторону, соответствующую (неверную, с нашей современной точки зрения) формулу следует считать доказанной в древнеегипетском понимании, ведь эта формула убедительно обоснована тем, что она (конечно, записанная не с помощью математических символов, а посредством слов) содержится в авторитетном документе.

Иначе обстояло дело в Древней Греции. Сравнительно (с Египтом) небольшие государственные образования с народными собраниями. В народных собраниях выступают ораторы, не являющиеся носителями априорного авторитета. Они должны убедить слушателей посредством рассуждения. Формулирование правильных рассуждений становится повседневной и актуальной потребностью. Отсюда – зарождение логики у Сократа и окончательное оформление её в виде науки у Аристотеля. Отсюда же – приближающиеся к современным представления о доказательстве, начало дедуктивного метода в математике. Основой математической убедительности становится рассуждение. Возникает понятие об основах правильных рассуждений – аксиомах и правилах логического вывода. Убедительно (и следовательно, доказуемо) то, что может быть получено «законным рассуждением» из отправных утверждений, признаваемых справедливыми. (Если задуматься над тем, какие дисциплины опираются на понятие доказательства, то окажется, что таких дисциплин две: математика и юриспруденция. По-видимому, местом их рождения следует признать Древнюю Грецию: именно там возникла культура убеждения путём рассуждения, в частности – путём прения сторон. В этом смысле математику можно назвать младшей сестрой юриспруденции.)

Наконец, Индия. Хотя те геометрические иллюстрации, на которые мы собираемся ссылаться, относятся к средневековой Индии, скорее всего, они появились уже в Индии древней. Вообще, датировка индийских математических представлений вызывает значительные трудности, поскольку одни тексты могут представлять собой изложение других, более ранних. С другой стороны, это и не так существенно: в то время как средневековый Египет и средневековая Греция не имели ничего общего с Древним Египтом и Древней Грецией, средневековая Индия оставалась хранителем духовного наследия Древней Индии. Существенной чертой этого наследия являлось и является придание статуса высшей достоверности внутреннему озарению. Непосредственное внутреннее озарение представляет собой основной источник знания и обладает неоспоримой убедительностью. То, что познано таким образом, считается доказанным. Чтобы убедить в этом другого, надо привести его в такое состояние, чтобы и он мог испытать внутреннее озарение. Поэтому геометрические доказательства выглядели так: чертёж, а под ним подпись «Смотри!».

Примеры таких чертежей с подписями «Смотри!», относящиеся к XII и XVI вв., приведены, например, в монографии [9, с. 76, 154]. Чертёж XIV в. (он воспроизведён также в статье [15, с. 75]), на наш взгляд, достоин того, чтобы излагаться в сегодняшней средней школе: он нагляднее современных доказательств показывает, что площадь круга равна площади прямоугольника, стороны которого суть полуокружность и полудиаметр круга. Поэтому мы приводим этот чертёж здесь (рис. 5).

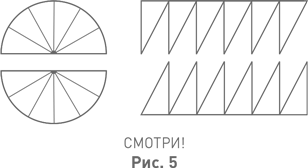
Автор отдаёт себе отчёт в том, что его мнение по поводу индийских доказательств расходится с мнением такого авторитета в области истории математики, как А. П. Юшкевич, который пишет [9, с. 155]: «Лаконичность выводов в индийских сочинениях по математике или наличие в последних чертежей с одной лишь припиской "Смотри!" не следует рассматривать как проявление особого подхода к проблеме доказательства или особого хода мышления». На наш взгляд, как раз следует. Почему же в противном случае такого рода «Смотри!» мы не встречаем нигде, кроме Индии?

На рис. 6 приведён ещё один чертёж с подписью «Смотри!». Он относится к XII в. и представляет собой доказательство теоремы Пифагора, опирающееся на формулу квадрата разности двух чисел.

Ценные соображения об эволюции понятия математического доказательства высказывает С. С. Демидов, который, в частности, указывает, «что доказательность математических рассуждений также в конечном итоге есть их убедительность. То, что нам казалось убедительным вчера, уже не кажется таким сегодня» [15].

Определение доказательств как убеждающего текста делает понятие доказательства довольно-таки субъективным (для кого текст убеждающий, а для кого нет). Нам это не представляется недостатком определения. Такова суть вещей. Употреблённое выше слово «делает», пожалуй, неудачно. Наше определение не столько делает понятие доказательства субъективным, сколько отражает субъективный характер этого понятия. Тем интереснее уяснить задачу, от решения которой мы весьма далеки: почему же всё-таки понятие доказательства носит характер общекультурный в том смысле, что в пределах одной и той же культуры споры о том, доказано или нет то или иное утверждение, хотя и возникают, но сравнительно редко?

Говоря о таких спорах, мы не имеем в виду несогласия между представителями разных логических направлений в математике: например, между представителями обычной (классической) и интуиционистской (конструктивистской) математики. Последние не признают доказанными (а, напротив, считают неверными) многие утверждения обычной математики. Можно считать, что интуиционисты (конструктивисты) принадлежат к другой математической культуре и даже самые привычные слова (такие, скажем, как «существует») наполняют другим смыслом [разумеется, интуиционисты (конструктивисты) считают, что это представители традиционной математики наполняют слова другим смыслом, а они, интуиционисты, как раз и употребляют эти слова в единственно правильном смысле]. Поэтому интуиционисты считают неверными многие доказательства традиционной математики.

Мы говорим здесь о другом – не об изменении семантики терминов, ведущем к изменению оценки истинности утверждений, а о том, что доказательство может оказаться непонятным и потому неубедительным (а раз неубедительным, значит, вообще не доказательством). Современная математика имеет сложное строение, постепенно становящееся необозримым. Доказательства некоторых теорем оказываются столь громоздкими, что проверка их требует чрезвычайно большого желания, терпения и времени. О владении специальными знаниями нечего и говорить: не только придумывание, но и проверка доказательств ряда теорем доступна лишь узкому кругу посвящённых. Именно так обстоит дело, например, с предложенным Уайлсом доказательством Великой теоремы Ферма.

Иногда интересуются объёмом доказательства той или иной теоремы. При этом обычно имеют в виду, что в доказательстве разрешается использовать в виде готовых формулировок, уже не требующих доказательств, теоремы, полученные ранее. Будет ли такое рассуждение доказательством, т. е. убеждающим текстом, для того, кто не знаком с доказательствами этих установленных ранее теорем? Мы не берёмся дать однозначный ответ на этот вопрос. Заметим ещё, что само слово «ранее» вносит дополнительный субъективный «релятивистский» момент (хронологическая последовательность двух почти одновременно доказанных теорем может по-разному определяться разными наблюдателями). Если же запретить ссылаться в доказательстве на какие бы то ни было ранее доказанные теоремы и восходить непосредственно к определениям и первичным, неопределяемым понятиям (о которых мы рассуждали в нашем первом размышлении), то такое полное доказательство может в ряде случаев простираться на тысячи страниц математического текста (и быть затруднительным для восприятия даже ещё более, чем доказательство, опирающееся на факты, хотя бы и неизвестные читателю, но ясно сформулированные).

Изучение трудных математических доказательств можно сравнить с альпинистским восхождением на вершину. Уровень моря соответствует начальным понятиям. Восхождение от уровня моря может занимать месяцы, а его математический аналог (понимание доказательства) – годы. В обоих случаях много промежуточных остановок. Первая – общий высокогорный лагерь, в котором собираются альпинисты, направляющиеся на различные окрестные вершины. Этому этапу соответствует получение серьёзной математической подготовки, достаточной для овладения более специальными темами. Затем начинается движение к избранной вершине, опять-таки с остановками в промежуточных лагерях. Для математика роль этих лагерей и остановок играют соответственно теории и теоремы. Как альпинист может совершить за свою жизнь ограниченное число восхождений, так и математик узнаёт ограниченное число доказательств.

Следующая общая для альпинизма и математики черта является существенной – это известная условность в выборе точки отсчёта. Собственно восхождение начинается не с уровня моря, а с точки, куда профессиональные альпинисты могут добраться как бы без труда, хотя для обычных людей попадание в эту точку может представить весьма большие трудности. Собственно доказательство начинается с аналогичной точки: эта точка расположена на некоем общекультурном (имеется в виду математическая культура) уровне. Впрочем, при современном состоянии математики область, очерчиваемая в сложных словах частью «обще-», постоянно уменьшается, и ныне многие доказательства начинаются с точки, доступной лишь узким специалистам. Ещё одна общая черта математики и альпинизма – расчленённость на этапы, наличие достаточного числа промежуточных остановок.

Откуда же у математика берётся убеждение, что доказанные теоремы, доказательства которых он так никогда и не узнáет, действительно являются доказанными, т. е. располагают доказательствами? Видимо, такое убеждение основано не на чём ином, как на доверии. Это положение внешне не должно казаться слишком странным. В самом деле, многие ли читатели этих строк видели остров Пасхи? Ведь убеждение не видевших остров в том, что он существует, также основано в конечном счёте на доверии. Но если современное доказательство основано на доверии к авторитету, то в чём же его принципиальное отличие от древнеегипетского?

Ответ на этот непростой вопрос заключается, возможно, в том, что доказательства постепенно переходят из разряда явлений индивидуального опыта в разряд явлений опыта коллективного. Тенденция к выдвижению на первый план коллективного вообще характерна для истории цивилизации. Хорошо известно (и подробно обсуждено), что с развитием человеческого общества возникают и неуклонно усиливаются разделение и кооперация труда. Лишь в глубокой древности человек мог сам, лично производить всё необходимое для себя; сейчас каждый вынужден пользоваться результатами труда других. Известно (хотя и не столь подробно обсуждено), что одновременно происходят разделение и кооперация научных знаний. Трудно сказать, когда – по-видимому, в Средние века – ещё находились отдельные учёные, способные охватить всю доступную их современникам сумму знаний. Сейчас каждый вынужден так или иначе использовать знания других. Аналогично обстоит дело и с доказательствами: деятельность в сфере производства и потребления доказательств стала в такой же степени объектом разделения и кооперации, как и деятельность в сфере производства и потребления знаний. Само понятие убедительности начинает терять свой индивидуализированный оттенок и всё больше приобретает коллективный характер. По-видимому, следует постепенно приучаться говорить об убедительности не для отдельного индивидуума, а для некоторого научного коллектива. При этом коллективная убедительность отнюдь не означает равную «непосредственную убедительность» для каждого в отдельности члена коллектива. Коллектив выступает не как простая сумма членов, а как единое целое. Смысл коллективной убедительности в том, что для каждой составной части доказательства найдётся свой «отвечающий за неё» член коллектива, для которого непосредственно убедительна именно эта часть (а другие члены коллектива полагаются в данном вопросе на этого члена).

Век информатики вносит свои коррективы и в представления о доказательствах. Возникают, например, случаи, когда доказательство требует перебора столь большого числа вариантов, что этот перебор делается недоступным человеку, а машине доступен. Допустим, машина перебрала все требуемые варианты и перебор привёл к нужным результатам. Можем ли мы считать, что получили доказательство? А что если машина дала так называемый сбой? (Но ведь и человек может ошибаться!) Кроме того, необходима гарантия, что сама программа (работы машины) составлена правильно; правильность программы требует особого доказательства, и теория таких доказательств образует специальный раздел теоретического программирования.

Реально компьютер был привлечён для решения проблемы четырёх красок. По простоте формулировки эта проблема, состоящая в доказательстве гипотезы четырёх красок, мало уступает проблеме Ферма (состоящей в доказательстве гипотезы Ферма), а по естественности постановки (и прикладному значению) её превосходит. Вот формулировка этой гипотезы в Большой Советской Энциклопедии (изд. 3-е, том 29, статья «Четырёх красок задача»): Четырёх различных красок достаточно для того, чтобы раскрасить любую карту так, чтобы никакие две области, имеющие общий участок границы, не были окрашены в один и тот же цвет. Проблема четырёх красок возникла в картографической среде: впервые наблюдение о достаточности четырёх красок было сделано в 1852 г. при составлении карты графств Англии. Обнаружилось, что гипотеза четырёх красок подтверждается во всех известных частных случаях. Сравнительно просто удаётся доказать (и это было сделано в 1890 г.), что для любой мыслимой карты достаточно пяти красок. Попытки же доказать аналогичное утверждение для четырёх красок долгое время (в течение ста лет) были безуспешны.

В 1976 г. Аппелем и Хакеном было анонсировано [17], а в 1977 г. изложено [18, 19] решение проблемы, основанное на сведéнии решения к большому числу частных случаев, рассмотрение которых можно поручить машине. Машина всё проверила, и таким образом было получено доказательство того, что всякую карту можно раскрасить четырьмя красками так, как нужно.

Казалось бы, проблема закрыта. Однако всё не так просто. Доказательство обладало двумя неприятными особенностями. Во-первых, рассуждения авторов были столь длинны и сложны, что никому не удавалось проверить их во всей полноте. Во-вторых, существенная часть доказательств состояла в использовании компьютера; именно компьютер, а не человек проверял, обладает ли каждая из почти двух тысяч специально отобранных карт некоторым требуемым качеством. Первая особенность была впоследствии устранена (если не полностью, то в очень большой степени) другими авторами, значительно упростившими первоначальные рассуждения Аппеля и Хакена. А вот избежать того, что в истинности большого числа фактов удостоверяется не человек, а компьютер, не удалось. А что если компьютер ошибся? Ведь такое иногда случается. Поэтому утверждение, что проблема четырёх красок решена, у многих вызывает сомнение.

Сами Аппель и Хакен высказывают такие мысли по поводу своего доказательства: «При доказательстве было осуществлено беспрецедентное применение компьютеров. Дело в том, что используемые в доказательстве вычисления делают его более длинным, чем традиционно считается допустимым. На самом деле правильность предложенного доказательства вообще не может быть проверена без помощи компьютера. Более того, некоторые из решающих идей доказательства материализовались посредством компьютерных экспериментов. Не исключено, конечно, что в один прекрасный день появится короткое доказательство теоремы о четырёх красках… Вместе с тем не исключено, что такое короткое доказательство вообще невозможно. В этом последнем случае возникает новый и интересный тип теорем, для которых не существует доказательств традиционного типа» [20].

Комментарий. Остановимся на ситуации с доказательством Аппеля и Хакена чуть подробнее. Основная идея этих авторов связана со следующими представлениями. Прежде всего авторы переходят от раскраски областей карты к раскраске вершин плоского графа, причём такого, который представляет собою триангуляцию. Далее они называют конфигурацией любой подграф, образованный циклом и внутренностью этого цикла. Конфигурация называется сводимой, если некоторыми стандартными методами можно доказать, что она не может быть вложена в минимальный контрпример к гипотезе четырёх красок. Множество конфигураций называется неизбежным, если каждая плоская триангуляция содержит как подграф одну из конфигураций множества. Из определений немедленно следует, что для решения (положительного) проблемы четырёх красок достаточно предъявить неизбежное множество сводимых конфигураций. Авторы предъявляют в явном виде 1834 сводимые конфигурации, образующие неизбежное множество [19, с. 505–567]. Длина цикла в каждой из этих конфигураций – 14 или менее того. И для поиска неизбежного множества, и для доказательства сводимости его членов использовался компьютер. Однако если в первом случае (построение множества) компьютер выполнял вспомогательные функции, поскольку само доказательство неизбежности найденного (теперь уже не важно, каким способом) множества не опирается на машинные вычисления, то во втором случае (проверка сводимости) использование компьютера являлось существенным компонентом доказательства, и на каждую конфигурацию ушло примерно 10 минут машинного времени такой проверки. Оценивая доказательство Аппеля и Хакена, авторы обзора [24] указывают, что для доказательства понадобилось четыре года и 1200 часов машинного времени и что текст его занимает 139 страниц, в том числе 99 страниц рисунков, в среднем более 30 рисунков на страницу. Они отмечают также, что «существенно переборный характер доказательства затрудняет его проверку (по оценке Аппеля, проверка всех деталей требует 300 часов машинного времени)». Названные 300 часов относятся, по-видимому, к проверке сводимости. Однако, как мы уже отмечали, сомнения вызывает как раз немашинная часть – проверка неизбежности предъявленного множества конфигураций. Дело в том, что непосредственно в тексте статей [18] и [19] эта проверка исчерпывающим образом не проводится. В статье [18, с. 460], в подстрочном примечании, сообщено, что детали доказательства неизбежности предъявленного множества (более точно, детали доказательства лежащей в основе этой неизбежности так называемой теоремы о разрежении) содержатся на микрофишах, образующих специальное приложение к журналу. Автор этих строк, изучавший журнал в библиотеке, указанного приложения, однако, не обнаружил.

Что же касается авторов обсуждаемого доказательства, то они отдавали себе отчёт в сложности его восприятия. В статье [33, с. 852] приводится следующая цитата из неназванной статьи Аппеля и Хакена 1986 г. (перевод даётся по статье [34, с. 95]):

Читатель должен разобраться в 50 страницах текста и диаграмм, 85 страницах с почти 2500 дополнительными диаграммами, 400 страницах микрофишей, содержащих ещё диаграммы, а также тысячи отдельных проверок утверждений, сделанных в 24 леммах основного текста. Вдобавок читатель узнаёт, что проверка некоторых фактов потребовала 1200 часов компьютерного времени, а при проверке вручную потребовалось бы гораздо больше. Статьи устрашающи по стилю и длине, и немногие математики прочли их сколько-нибудь подробно.

Доказательство Аппеля и Хакена продолжало вызывать сомнения до конца XX в. Вот что пишет Робин Томас, автор упомянутой статьи [33]:

[…] Трудности с доказательством Аппеля и Хакена можно уложить в два пункта:

1. Часть доказательства основана на использовании компьютера и не может быть проверена вручную;

2. Даже та часть, для которой ручная проверка предполагается возможной, не подвергалась, насколько мне известно, независимой проверке.

Далее Р. Томас указывает, что он и трое его коллег (N. Robertson, D. P. Sanders, P. Seymour) пытались проверить доказательство Аппеля и Хакена, но вскоре сдались и поняли, что разумнее разработать собственное доказательство. Что они и сделали. Доказательство четырёх авторов следует основным идеям Аппеля и Хакена и не устраняет трудности (1), но в значительной мере ликвидирует трудность (2), будучи гораздо более проверяемым в своей некомпьютерной части. Тем не менее и это новое доказательство вызывает скептицизм. Вот что пишет о нём А. В. Самохин, завершая свою статью [34]:

Компьютерная часть всё ещё остаётся скорее предметом веры. Ведь даже проверка распечаток всех программ и всех входных данных не может гарантировать от случайных сбоев или даже от скрытых пороков электроники (вспомним, что ошибки при выполнении деления у первой версии процессора Pentium были случайно обнаружены спустя полгода после начала его коммерческих продаж – кстати, математиком, специалистом по теории чисел). По-видимому, единственный способ проверки компьютерных результатов – написать другую программу и для другого типа компьютера. Это, конечно, совсем не похоже на стандартный идеал дедуктивных рассуждений, но именно так осуществляется проверка утверждений во всех экспериментальных науках. Из которых математика, стало быть, исключена напрасно.

Создаётся впечатление, что с развитием математики (и появлением всё более и более сложных и длинных доказательств) доказательства теряют своё главное свойство – свойство убедительности. Непонятно, что же тогда остаётся от доказательства, ведь убедительность является их свойством по определению. Кроме того, с усложнением доказательства возрастает элемент его субъективности. Конечно, формальное доказательство объективно. Но, во-первых, формальными доказательствами обладают не сами суждения, а их выражения, записи в формализованных языках. Во-вторых, проверка утверждения, что данный текст является формальным доказательством, хотя и осуществляется алгоритмически, может при объёмистом тексте вызвать значительные практические трудности.

Большие доказательства начинают жить по каким-то своим макроскопическим законам. При чрезмерном возрастании объёма доказательства расплывается само представление о доказательстве, подобно тому как в «большом» расплывается понятие о натуральном числе (ещё раз отсылаем читателя к статье П. К. Рашевского [16]).

Получается, что, хотя все доказательства должны по определению быть убедительными, одни из них убедительнее других, т. е. как бы являются доказательствами в большей степени, чем другие. Возникает нечто вроде градации доказательств по степени доказательности – явление, которое, конечно, в корне противоречит первоначальным представлениям об одинаковой непреложности всех доказательств. Но ведь и математические истины допускают нечто вроде такой градации. Каждое из следующих трёх утверждений: «2 · 2 = 4», «17¹⁴ > 31¹¹», «300! > 100³⁰⁰» – истинно. Однако мы говорим: «Верно, как 2 · 2 = 4», но не говорим: «Верно, как 17¹⁴ > 31¹¹» или «Верно, как 300! > 100³⁰⁰».

Назад: 5. «Можно ли доказать, что великую теорему ферма нельзя ни доказать, ни опровергнуть?»

Дальше: 7. Можно ли сделать математику понятной?