Книга: Апология математики (сборник статей)
Назад: 3. Можно ли определить натуральный ряд (с прописной буквы)?
Дальше: 5. «Можно ли доказать, что великую теорему ферма нельзя ни доказать, ни опровергнуть?»
4. Можно ли аксиоматически определить понятие натурального ряда (со строчной буквы)?
Итак, приступим к попыткам определить аксиоматически понятие натурального ряда – структуры, изоморфной Натуральному Ряду. Как только произносится слово «изоморфизм», тем самым предполагается, что указано, какие отношения и операции должны сохраняться при этом изоморфизме. Следовательно, мы должны прежде всего точно указать, какие отношения и операции мы желаем рассматривать на Натуральном Ряду и изоморфных ему натуральных рядах. В число этих операций могут быть включены нольместные операции (т. е. индивидные константы; например, индивидную константу «ноль» можно рассматривать как нольместную операцию) и одноместные отношения (т. е. свойства). Указание этих выделенных операций и отношений в значительной мере произвольно. Например, можно рассматривать Натуральный Ряд (а значит, и любой изоморфный ему натуральный ряд): 1) как структуру лишь с отношением порядка «<», или 2) как структуру с выделенным элементом «ноль» и операцией «переход к следующему», или 3) как структуру, в которой помимо уже названных отношений и операций выделены ещё операции сложения и умножения.
Для наших целей нагляднее всего не задавать никаких операций, а задать лишь отношение порядка «<». Итак, мы рассматриваем каждый натуральный ряд как множество, на котором определено бинарное отношение порядка «<». Именно свойства такой математической структуры мы и будем исследовать.
Перейдём к перечислению этих свойств. Каждое свойство отношения «<» в произвольном натуральном ряду должно (в силу наличия изоморфизма) иметь место и в обычном Натуральном Ряду, когда отношение «<» понимается как обычное отношение порядка между натуральными числами. После этого замечания сформулируем несколько таких свойств.
1. Отношение «<» транзитивно. В символах:
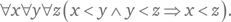
2. Отношение «<» антирефлексивно. В символах:

3. Отношение «<» связно. В символах:

Эти три свойства в своей совокупности утверждают просто-напросто, что «<» есть отношение строгого линейного порядка.
Прежде чем двигаться дальше, остановимся и задумаемся: а зачем, собственно, мы перечисляем эти свойства? А вот зачем. Мы надеемся, что, перечислив некоторое число свойств, мы сумеем дать аксиоматическое определение натурального ряда. Более подробно, наш план таков. Сперва мы выписываем некоторое число характерных для Натурального Ряда свойств. Затем мы объявляем эти свойства аксиомами и определяем натуральный ряд как произвольную математическую структуру, удовлетворяющую выписанным аксиомам. Мы не претендуем на то, что ровно одно определённое множество с заданным на нём бинарным отношением «<» будет удовлетворять нашим аксиомам (такая претензия была бы совершенно нереальна), но претендуем на то, что все такие множества (с заданным на них отношением) окажутся изоморфными между собой. А поскольку наши аксиомы будут выполняться на Натуральном Ряду (так мы будем выбирать аксиомы), то Натуральный Ряд будет одной из попарно изоморфных структур, удовлетворяющих аксиомам, и, значит, все эти изоморфные между собой структуры будут изоморфны и Натуральному Ряду. Если нам удастся достичь изложенной только что цели, мы и будем считать, что сумели аксиоматически определить натуральный ряд.
Можем ли мы, имея в виду поставленную цель, довольствоваться тремя выписанными свойствами – аксиомами? Разумеется, нет. Этим аксиомам удовлетворяют все линейно упорядоченные множества, среди которых много неизоморфных и, следовательно, заведомо неизоморфных Натуральному Ряду N. Например, множество R всех действительных чисел с обычным отношением порядка будет удовлетворять выписанным трём аксиомам. Наблюдая совместно N и R, мы замечаем, что N имеет по крайней мере два свойства, которых нет в R. Вот они.
4. В N есть наименьший элемент. В символах:

5. В N за каждым элементом х непосредственно следует некоторый у. («Непосредственно» – это значит, что между х и у нет третьего элемента.) В символах:

Эти пять аксиом уже значительно сужают круг удовлетворяющих им линейно упорядоченных множеств. Этим аксиомам удовлетворяет Натуральный Ряд, а также, например, такое множество действительных чисел (рассматриваемое с обычным порядком):

Наличие этой, отличной от N, структуры (*), удовлетворяющей аксиомам 1–5, ещё не служит препятствием к тому, чтобы считать эти аксиомы аксиоматическим определением натурального ряда, ведь эта структура изоморфна N (и, таким образом, может признаваться натуральным рядом). Графическое изображение порядка на (*) (и на N) приведено на рис. 1.
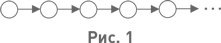
Легко заметить, однако, что аксиомам 1–5 удовлетворяет и такая структура (т. е. множество плюс отношение порядка):
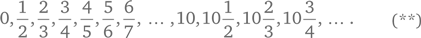
Графический образ этой порядковой структуры приведён на рис. 2.

В этой структуре у двух элементов (у 0 и 10) нет непосредственных предшественников. Запретим эту ситуацию следующей аксиомой 6.
6. Если у двух элементов х1 и х2 нет непосредственных предшественников, то они равны. В символах:
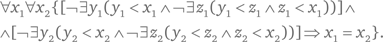
Аксиома 6 исключает структуру (**), но не исключает такой структуры:
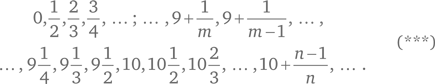
Структура (***), очевидно, не изоморфна натуральному ряду. Её графический образ приведён на рис. 3.
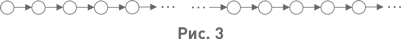
Наша цель, подобно горизонту, отодвигается всё дальше и дальше… Оказывается, она вообще недостижима. Оказывается, имеет место следующий замечательный факт: сколько бы мы ни выписывали аксиом, использующих логические знаки, знак отношения «<» и переменные, пробегающие по элементам определяемой структуры, у совокупности выписанных аксиом всегда будет модель, не изоморфная натуральному ряду. Ввиду фундаментальной важности этого факта (означающего невозможность аксиоматического определения натурального ряда с использованием указанных средств) изложим его подробнее.
Будем записывать аксиомы на формализованном символическом языке, в алфавит которого входят следующие знаки:
1. Знаки препинания: левая скобка «(» и правая скобка «)»;
2. Логические знаки «¬», «∧», «∨», «⇒», «∀», «∃», «=»;
3. Индивидные переменные х, у, z, и, v, w, х1, y1, z1, u1, v1, w1, …;
4. Знак «<».
С помощью этих букв по естественным и легко формулируемым синтаксическим правилам составляются формулы. Простейшие примеры формул:
х < у ∨ у < х; ∀х (х < х);
∃ х ∃у (у < х ⇒ у < х);
∃ у (х < у); ∀ х ∃у (х < у).
Возьмём теперь какое-либо множество с каким-либо определённым на нём бинарным отношением (не обязательно отношением строгого порядка), обозначаемым через «<». Всякое такое множество с отношением «<» будем называть структурой сигнатуры <. Таким образом, структура сигнатуры < состоит из множества (называемого носителем структуры) и отношения «<». Назначим для каждой индивидной переменной носитель структуры в качестве области изменения этой переменной. Тогда каждая формула становится либо высказыванием, как вторая, третья и пятая формула из приведённого только что списка, либо высказывательной формой, как первая и четвёртая формулы. Формулы, превращающиеся в высказывания, называются закрытыми, только их мы и будем впредь рассматривать. Про (закрытую) формулу, становящуюся – при рассмотрении на данной структуре – истинным высказыванием, говорят, что она истинна на данной структуре или выполняется на данной структуре, а про структуру – что она удовлетворяет данной формуле.
Среди структур сигнатуры < выделена структура N – наш обычный Натуральный Ряд с обычным отношением порядка. Будем называть аксиомой любую закрытую формулу, превращающуюся в истинное высказывание при интерпретации на структуре N. Так вот, какое бы – конечное или бесконечное – количество аксиом мы ни выписывали, всегда найдётся такая структура сигнатуры <, которая, во-первых, удовлетворяет всем выписанным аксиомам и, во-вторых, не изоморфна N.
Получается, таким образом, что натуральный ряд нельзя определить аксиоматически: ведь определить N аксиоматически – это значит записать такую систему аксиом, которая определяла бы N с точностью до изоморфизма (это, в свою очередь, значит, что любые две структуры, удовлетворяющие всем выписанным аксиомам, изоморфны).
«Позвольте, – снова возразит читатель, – но аксиомы Пеано ведь определяют Натуральный Ряд как раз с точностью до изоморфизма. Система аксиом Пеано категорична, а это как раз и означает, что все её модели изоморфны». Немножко терпения, разберёмся и с аксиомами Пеано.
А сейчас обсудим вот какой вопрос. На Натуральном Ряде определено не только отношение порядка «<», но и бесчисленное множество других отношений и операций. Среди них двуместное (или бинарное) отношение делимости двух чисел; трёхместное (или тернарное) отношение «х + у = z»; одноместное (или сингулярное, singulary) отношение «быть простым числом» (напомним, что свойства мы трактуем как одноместные отношения); двуместная операция сложения; двуместная операция умножения; двуместная операция возведения в степень (причём 00 = 1); одноместная операция непосредственного следования (мы будем, как это часто делается, обозначать её штрихом, так что, например, 0' = 1; 13' = 14); константы 0, 1, 2, 3, 4, … (напомним, что константы мы трактуем как нольместные операции); четырёхместная операция [logu+2 z! + yx·z+u] (здесь, как обычно, через [a] обозначается целая часть числа a); и многие другие. Мы привели лишь несколько примеров, а всего на N определено несчётное количество операций и отношений. Для того чтобы определить понятие структуры, изоморфной N, мы сперва должны из этого количества выделить некоторые (теоретически возможно – все) операции и отношения и рассмотреть изоморфизм относительно именно этих выделенных операций и отношений. На самом деле поэтому не существует понятия натурального ряда просто, а только понятие натурального ряда относительно данного списка операций и отношений. Выше мы рассматривали понятие натурального ряда относительно списка, в котором операций не было вовсе, а отношение одно – отношение «быть меньше».
Выделенные на множестве операции и отношения, а также выделенные элементы множества (таковых у нас пока не было) называют в контексте наших рассмотрений сигнатурными, а список таких операций и отношений – сигнатурой. Точнее, сигнатурой называют список не самих выделенных элементов, операций и отношений, а список их имён, но для наших целей это различие (само по себе очень важное) не слишком существенно, и нам проще его не замечать.
Множество с выделенными операциями и отношениями, образующими список σ, называется (математической) структурой сигнатуры σ. Теперь мы можем сказать, что всякий натуральный ряд является структурой той или иной сигнатуры σ. Поэтому следует говорить не о натуральном ряде вообще, а о натуральном ряде сигнатуры σ. До сих пор мы рассматривали случай, когда
σ = {<}.
Может быть, причина нашего неуспеха в попытке определить аксиоматически натуральный ряд вызвана именно бедностью сигнатуры? Давайте расширять сигнатуру и наблюдать, чтó при этом будет происходить.
Сперва добавим в сигнатуру константу «0» (для обозначения наименьшего, относительно порядка «<», элемента) и штрих «'» для обозначения операции непосредственного следования. На Натуральном Ряде N эти объекты подчинены аксиомам (свойствам) 7 и 8 (сравните свойства 4 и 5, которые вытекают из свойств 7 и 8).
7. ∀y (0 = у ∨ 0 < у).
8. ∀x (x < x' ¬ ∃ z (x < z ∧ z < x')).
Всякий натуральный ряд с сигнатурой {0, ', <} изоморфен, по определению, Натуральному Ряду N, причём изоморфизм рассматривается относительно {0, ', <}. Поэтому всякий такой натуральный ряд состоит из элементов 0, 0', …, упорядоченных следующим образом: 0 < 0' < 0'' < 0''' <…
замечание. Следует отдавать себе отчёт, что в каждом натуральном ряду свой 0, свой ' и своё <, т. е. свой элемент, обозначенный через «0», своя операция, обозначенная через «'», и своё отношение, обозначенное через «<». Строго говоря, для каждого натурального ряда мы должны были бы придумать своё обозначение этих объектов: например, если мы рассматриваем натуральный ряд M, то нужно прибавлять эту букву M в качестве индекса к знакам «0», «'», «<». Эта строгость создаёт некоторое удобство. Однако отсутствие строгости тоже создаёт некоторое удобство. Считается, что в данном случае удобство от нестрогости больше, и поэтому одним и тем же знаком «0» обозначаются различные элементы (но в каждом натуральном ряду – один и только один элемент; в частности, в Натуральном Ряду – мощность пустого множества). Аналогично знак «<» обозначает различные отношения (но в каждом натуральном ряду только одно) и знак «'» обозначает различные операции (но в каждом натуральном ряду – только одну). Сказанное сохраняет силу не только для натуральных рядов, но и для любых структур сигнатуры {0, ', <}, не обязательно изоморфных N.
Посмотрим теперь, как выглядит произвольная структура сигнатуры {0, ′, <}, подчиняющаяся аксиомам 1–8 (аксиомы 4 и 5 следуют из аксиом 7 и 8, но в этом нет большой беды). Она, очевидно, представляет собой линейно упорядоченное множество, в котором 0 есть наименьший элемент, 0′ – непосредственно следующий за 0 элемент (так что между 0 и 0′ ничего нет), 0′′ – непосредственно следующий за 0′ элемент и т. д. Все эти элементы 0, 0′, 0′′, 0′′′′, … образуют начальный отрезок нашей структуры. Этот начальный отрезок называется стандартной частью структуры, а оставшаяся часть (она может быть и пустой) – нестандартной. Стандартная часть изоморфна Натуральному Ряду N. Если бы оказалось, что в любой структуре сигнатуры {0, ′, <}, подчиняющейся аксиомам 1–8, нет ничего, кроме стандартной части, то наша цель была бы достигнута: аксиомы 1–8 давали бы в своей совокупности искомое аксиоматическое определение натурального ряда, точнее, натурального ряда сигнатуры {0, ′, <}.
Однако это не так, поскольку структура, графически изображённая на рис. 3, такая, скажем, как (***), где
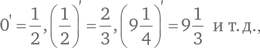
удовлетворяет аксиомам 1–8, но не изоморфна N: в ней есть непустая нестандартная часть (на рис. 3 эта нестандартная часть изображена справа), в (***) эта нестандартная часть состоит из элементов вида  Более того, оказывается, что никакие аксиомы не могут задать натуральный ряд сигнатуры {0, ', <}, поскольку структура на рис. 3 всегда будет моделью для таких аксиом.
Более того, оказывается, что никакие аксиомы не могут задать натуральный ряд сигнатуры {0, ', <}, поскольку структура на рис. 3 всегда будет моделью для таких аксиом.
 Более того, оказывается, что никакие аксиомы не могут задать натуральный ряд сигнатуры {0, ', <}, поскольку структура на рис. 3 всегда будет моделью для таких аксиом.
Более того, оказывается, что никакие аксиомы не могут задать натуральный ряд сигнатуры {0, ', <}, поскольку структура на рис. 3 всегда будет моделью для таких аксиом.Может быть, дело всё ещё в бедности сигнатуры? Что будет, если добавить сложение и умножение и рассматривать натуральный ряд не сигнатуры {0, ', <}, а сигнатуры {0, ', <, +, ·}? Можно ли для такой более богатой сигнатуры составить список аксиом, определяющих понятие натурального ряда этой сигнатуры, т. е. выделить из всех структур этой сигнатуры те структуры, которые относительно 0, ', <, +, · изоморфны N? Оказывается, нет, нельзя. Какую бы совокупность аксиом – конечную или бесконечную – мы ни образовали, всегда для этой совокупности будут существовать структуры (сигнатуры {0, ', <, +, ·}), не изоморфные N. Более того, какую бы мы ни взяли сигнатуру и какую бы ни взяли для этой сигнатуры систему аксиом, всегда будет существовать модель этой системы аксиом, не изоморфная Натуральному Ряду N. Такие неизоморфные N модели называют нестандартными, а аксиомы, перечисляющие свойства натурального ряда (особенно, когда в сигнатуру входят «+» и «·»), называют аксиомами арифметики. Поэтому сказанное можно выразить и так: для любой системы аксиом арифметики существует нестандартная модель.
Если в число аксиом входят аксиомы 1–8 или какие-нибудь им равносильные, то в любой модели можно выделить стандартную часть 0, 0', 0'', …; нестандартность модели означает в этом случае непустоту нестандартной части. Эта нестандартная часть может оказаться устроенной более сложно, чем на рис. 3. На рис. 3 нестандартная часть подобна с точки зрения порядка множеству Z всех целых чисел. При естественных же аксиомах для сигнатуры, включающей операцию сложения, нестандартная часть всякой счётной (т. е. насчитывающей счётное число элементов) структуры, удовлетворяющей этим аксиомам, имеет вид, который мы (не очень удачно) пытались изобразить на рис. 4. На этом рисунке мы пытались как-то выразить следующую идею: берётся очень много (бесконечное счётное число) экземпляров множеств целых чисел Z, и эти экземпляры располагаются так, как расположено множество всех рациональных чисел Q.

Итак, предъявить систему аксиом, определяющую понятие натурального ряда (какой угодно сигнатуры), невозможно. Более подробная расшифровка этого утверждения, как мы знаем, такова: какие ни выбрать определённые на N операции и отношения, не может быть такой системы аксиом, все модели которой изоморфны N относительно этих операций и отношений.
Вот теперь и ответим на в опрос: а как же аксиомы Пеано?
Классические аксиомы Пеано с несущественными изменениями устроены так. Рассматривается сигнатура {0, '}. Формулируются три аксиомы.
I. ¬ ∃ x (x′ = 0).
II. ∀ x ∀ у (x' = у' ⇒ x = у).
III. Аксиома индукции.
Третью аксиому, аксиому индукции, мы пока только назвали, но не выписали. Теперь выпишем её:
∀Р {[Р(0) ∧ ∀x (Р(x) ⇒ Р(x'))] ⇒ ∀xР(x)}.
Приглядимся к аксиоме индукции. Мы замечаем, что в ней наряду с обычной индивидной переменной встречается ещё переменная Р. Разъясним смысл этой переменной. Прежде всего напомним, что семантика формулы (т. е. придание этой формуле смысла) возникает лишь после того, как предъявляется математическая структура соответствующей сигнатуры. В частности, чтобы обрели смысл аксиомы Пеано (формулы I–III), надо предъявить какую-либо структуру сигнатуры {0, '}, т. е. множество с выделенным элементом, обозначенным через «0», и выделенной одноместной операцией, обозначенной через «'». Тогда сразу определяется область изменения переменной x (как и всякой индивидной переменной): это есть множество всех элементов рассматриваемой структуры. Какова же область изменения переменной Р?
Переменная Р – особая, не встречавшегося ещё в нашем изложении типа. Её область изменения состоит из всевозможных свойств (= одноместных отношений), определённых на рассматриваемой структуре, т. е. свойств элементов этой структуры.
Понятие свойства относится к первичным и постигается из примеров. На натуральных числах определено, например, свойство чётности: каждое число может быть либо чётным, либо нечётным. Здесь несущественно, что бывают как чётные, так и нечётные числа; нас устроила бы ситуация, когда все числа – чётные; важно, что для каждого числа осмыслен вопрос, чётное оно или нечётное. А вот свойство зелёности не определено на натуральном ряду; для числа «быть зелёным» бессмысленно. Выше мы сформулировали некоторые свойства, какими как целое обладает Натуральный Ряд. Свойствами могут обладать и отношения: так, среди отношений выделяются, например, транзитивные. Но в данный момент нас интересуют свойства элементов рассматриваемой структуры (для которой выполняются аксиомы Пеано). Именно эти свойства могут выступать в качестве значений переменной Р.
Тот факт, что элемент a обладает свойством Q, записывается как Q(a). Если на элементах какого-то множества М определено свойство Q, то можно ввести в рассмотрение подмножество K этого множества, состоящее из тех и только тех элементов М, которые обладают свойством Q:
(x ∈ K) ⇔ Q(x). (!)
И наоборот, для каждого подмножества K можно ввести свойство Q – «быть элементом K», и опять-таки будет выполнено соотношение (!). Таким образом, свойство – это почти то же самое, что подмножество: «язык свойств» и «язык подмножеств» тривиально переводимы один в другой. (На языке подмножеств, например, аксиома индукции записывалась бы так:
∀ P{[0 ∈ Р ∧ ∀ x (х ∈ Р ⇒ х' ∈ Р)] ⇒ ∀ x (x ∈ Р)}.)
Итак, область изменения переменной Р в аксиоме индукции – совокупность всех свойств, определённых на рассматриваемой структуре. Посмотрим, как эта аксиома используется для того, чтобы установить, что удовлетворяющая аксиомам Пеано структура изоморфна N. Пусть структура сигнатуры {0, '} удовлетворяет аксиомам I–III. Аксиомы I–II обеспечивают наличие в этой структуре стандартной части {0, 0', 0'', 0''', …}. Теперь применим аксиому индукции, взяв в качестве значения переменной Р такое свойство P0 элементов структуры: «принадлежать к стандартной части». Аксиома гласит, что нечто справедливо для всякого Р, в частности для этого P0. Таким образом:
[Р0(0) ∧ ∀ x (Р0(х) ⇒ Р0(х'))] ⇒ ∀ xР0(x).
Заключённая в квадратные скобки посылка, очевидно, истинна (0 принадлежит стандартной части, и если x принадлежит стандартной части, то принадлежит и x'); поэтому ∀ xР0(x), т. е. все x (все элементы структуры!) принадлежат стандартной части. Стандартная часть, как уже было замечено, изоморфна N. Этим завершается доказательство того, что рассматриваемая структура изоморфна N.
Таким образом, всякая структура, удовлетворяющая аксиомам Пеано, изоморфна N, и, следовательно, эти аксиомы определяют понятие натурального ряда с сигнатурой {0, '}. Вроде бы это обстоятельство противоречит неоднократно делавшемуся нами заявлению, что системы аксиом с таким свойством не может быть.
Однако противоречия нет, и вот почему. Ранее речь шла лишь о свойствах Натурального Ряда, которые можно выразить определёнными языковыми средствами, иными словами, об аксиомах, записанных на определённом языке. В этом языке был лишь один вид переменных – индивидные переменные x, y, z, …. Сущность этих индивидных переменных заключается в том, что при интерпретации на какой-либо структуре областью изменения каждой из этих переменных объявляется одно и то же множество – множество всех элементов рассматриваемой структуры. В аксиоме же индукции участвует переменная другого вида – переменная Р. Её значениями являются не элементы рассматриваемой структуры, а свойства этих элементов (иначе, определённые на этих элементах одноместные предикаты, отчего сама переменная Р называется предикатной, точнее, предикатной переменной валентности 1). Таким образом, аксиома индукции – это формула другого, расширенного языка, более широкого, нежели рассматривавшийся до сих пор узкий язык. (Узкий потому, что в нём бывают только индивидные переменные.) А когда мы говорили, что систем аксиом, полностью характеризующих натуральный ряд, не бывает, мы имели в виду этот прежний, узкий язык.
Разъяснение, конечно, дано, но вряд ли оно кого-нибудь удовлетворит. Что с того, что на каком-то языке нельзя написать систему аксиом натурального ряда? Это, как говорится, «факт не биографии натурального ряда, а биографии этого языка». Просто-напросто узкий язык плохой, а вот теперь мы нашли хороший, расширенный язык, на котором как раз и возможно выписать адекватные аксиомы натурального ряда.
Однако всё не так просто. Грубо говоря, дело обстоит как раз наоборот: узкий язык «хороший», а расширенный – «плохой».
Попробуем разъяснить ситуацию. Начнём с терминологии. Формулы, в которых все переменные индивидные, называются элементарными, а язык, в котором допускаются только элементарные формулы, – элементарным. Синонимом для термина «элементарный» в данном контексте является термин «1-го порядка», или «первопорядковый». Все рассматриваемые выше аксиомы, кроме аксиомы индукции (т. е. все аксиомы 1–8 и I–II), были элементарными аксиомами, т. е. элементарными формулами. Не существует никакой (ни конечной, ни бесконечной и притом любой сигнатуры) системы элементарных аксиом, которой удовлетворял бы Натуральный Ряд N и все модели которой были бы изоморфны Натуральному Ряду N.
Бывают и неэлементарные формулы, но они принадлежат неэлементарному языку. В этом языке допускаются переменные более сложной природы – предикатные переменные валентности 1, значениями которых служат свойства (= одноместные отношения), предикатные переменные валентности 2, значениями которых служат бинарные (= двуместные) отношения и т. п., а также функциональные переменные (значением функциональной переменной валентности 1 может быть любая одноместная операция, такая, скажем, как «следование за», а значением функциональной переменной валентности 2 может быть любая двуместная операция, такая, скажем, как сложение). Аксиома индукции служит примером неэлементарной формулы. Более точно, неэлементарный язык с описанными только что возможностями называется языком 2-го порядка: это значит, что в нём допускаются переменные, пробегающие по отношениям и операциям (каковые отношения и операции должны быть определены на элементах структуры), но не рассматриваются более сложные переменные, значениями которых могут служить, скажем, свойства операций или операции над отношениями (или свойства отношений, такие как транзитивность). Аксиома индукции служит примером неэлементарной формулы языка 2-го порядка (или просто примером формулы 2-го порядка).
Казалось бы – и наличие аксиом Пеано это как бы подтверждает – возможна система неэлементарных аксиом 2-го порядка (т. е. аксиом, записанных в виде формул этого неэлементарного языка), определяющая понятие натурального ряда в следующем точном смысле:
1) N является моделью этой системы;
2) всякая модель этой системы изоморфна N.
Однако здесь возникают неожиданные, но совершенно фундаментальные трудности семантического (можно даже сказать – гносеологического) характера. Дело в том, что уже для языка 2-го порядка (не говоря уже о более сложных неэлементарных языках) само понятие модели теряет необходимую ясность. Это положение иллюстрируется следующим примером, связанным с так называемой проблемой континуума.
Как известно, количество элементов какого-либо множества называется кардинальным числом, или мощностью, этого множества. Понятие кардинального числа, или мощности, является обобщением понятия натурального числа, поскольку натуральные числа – это мощности конечных множеств. Среди бесконечных мощностей выделяются следующие две: мощность множества всех натуральных чисел и мощность множества всех действительных чисел (или всех точек какой-либо прямой). Первая обозначается 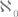 (читается «áлеф-ноль») и называется счётно-бесконечной мощностью (или бесконечной счётной, а чаще – просто счётной, хотя нередко бывает полезным называть счётными не только счётно-бесконечные, но и конечные мощности, т. е. натуральные числа); вторая обозначается
(читается «áлеф-ноль») и называется счётно-бесконечной мощностью (или бесконечной счётной, а чаще – просто счётной, хотя нередко бывает полезным называть счётными не только счётно-бесконечные, но и конечные мощности, т. е. натуральные числа); вторая обозначается  (строчное готическое «це») и называется мощностью континуума, континуальной мощностью. Эпитеты «счётно-бесконечный» («бесконечный счётный», «счётный») и «континуальный» распространяются и на множества соответствующих мощностей. Очевидно,
(строчное готическое «це») и называется мощностью континуума, континуальной мощностью. Эпитеты «счётно-бесконечный» («бесконечный счётный», «счётный») и «континуальный» распространяются и на множества соответствующих мощностей. Очевидно, 
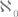 (читается «áлеф-ноль») и называется счётно-бесконечной мощностью (или бесконечной счётной, а чаще – просто счётной, хотя нередко бывает полезным называть счётными не только счётно-бесконечные, но и конечные мощности, т. е. натуральные числа); вторая обозначается
(читается «áлеф-ноль») и называется счётно-бесконечной мощностью (или бесконечной счётной, а чаще – просто счётной, хотя нередко бывает полезным называть счётными не только счётно-бесконечные, но и конечные мощности, т. е. натуральные числа); вторая обозначается  (строчное готическое «це») и называется мощностью континуума, континуальной мощностью. Эпитеты «счётно-бесконечный» («бесконечный счётный», «счётный») и «континуальный» распространяются и на множества соответствующих мощностей. Очевидно,
(строчное готическое «це») и называется мощностью континуума, континуальной мощностью. Эпитеты «счётно-бесконечный» («бесконечный счётный», «счётный») и «континуальный» распространяются и на множества соответствующих мощностей. Очевидно, 
Знаменитая проблема континуума состоит в выяснении того, существует или нет промежуточная мощность, т. е. мощность 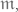 удовлетворяющая неравенству
удовлетворяющая неравенству
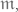 удовлетворяющая неравенству
удовлетворяющая неравенству
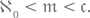
Знаменитая континуум-гипотеза состоит в том, что такой мощности нет. Философский смысл континуум-гипотезы очевиден: не существует количества, промежуточного между количеством всех натуральных чисел и количеством всех точек прямой линии (или равным ему количеством всех действительных чисел)! Эквивалентная формулировка континуум-гипотезы: всякая бесконечная часть континуального (т. е. имеющего континуальную мощность) множества либо сама имеет мощность континуума, либо же имеет счётно-бесконечную мощность.
историческая справка. Континуум-гипотезу высказал ещё в XIX в. Георг Кантор (1843–1918) – великий немецкий (впрочем, родившийся в Санкт-Петербурге и проведший там первые одиннадцать лет жизни) философ и математик, создатель теории множеств. Он высказал эту гипотезу не как гипотезу, а как положительное утверждение. А именно: в написанной в 1877 г. статье «К учению о многообразиях» [27, с. 257; 29, с. 132] Кантор заявил, что всякое бесконечное множество точек на прямой имеет либо континуальную, либо счётно-бесконечную мощность и что это утверждение устанавливается «с помощью индуктивного рассуждения, которое мы не будем здесь приводить». «Строгое исследование этого вопроса, – завершалась статья, – мы откладываем до другого раза». И действительно, с 1879 г. Кантор начал отдельными порциями публиковать трактат под названием «О бесконечных линейных точечных многообразиях»; эта серия публикаций должна была увенчаться доказательством заявленного утверждения. В шестой публикации [28] названной серии это утверждение и в самом деле было доказано, но лишь для узкого класса множеств (а именно для так называемых замкнутых множеств). Соответствующая теорема была сформулирована в самом конце статьи [28], и её формулировка сопровождалась утверждением, что «эта замечательная теорема» (dieser merkwürdige Satz) остаётся справедливой и для произвольных множеств и что это будет доказано в последующих параграфах трактата. Таким образом, Кантор, во-первых, доказал, что не существует такого количества, промежуточного между счётно-бесконечным и континуальным, которое служило бы количеством элементов какого-либо замкнутого множества на прямой линии, а также, во-вторых, обещал предъявить доказательство более сильного утверждения, а именно: что ни для какого (а не только замкнутого) множества точек на прямой линии количество этих точек не может быть промежуточным. Статье [28], завершённой 15 ноября 1883 г., суждено было стать последней в серии. Кантор обнаружил, что не в состоянии выполнить своё обещание, поскольку не располагает доказательством для общего случая. Это осознание имело драматические последствия. В мае 1884 г. Кантора постиг первый приступ нервной болезни. Через месяц приступ прошёл, но болезнь уже не отпускала свою жертву, а с 1899 г. приступы участились. После 1897 г. Кантор уже ничего не публиковал, а в 1918 г. умер в нервной клинике.
Ныне известно (в силу результатов, полученных К. Гёделем и П. Коэном), что ни доказать, ни опровергнуть континуум-гипотезу невозможно. Говоря «доказать» и «опровергнуть», мы имеем в виду все мыслимые средства, допускаемые современной математикой. А значит, повисает в воздухе вопрос о самом смысле континуум-гипотезы. В самом деле, смысл утверждения, истинность или ложность которого заведомо нельзя установить никакими средствами, воспринимается как туманный. Эта чрезвычайная ситуация радикально отличается от такого часто встречающегося положения, когда мы просто чего-то не знаем (но хотя бы ясно понимаем сам вопрос).
Оказывается, что можно выписать формулу 2-го порядка, которая тогда и только тогда имеет модель (т. е. такую структуру, в которой она становится верна), когда континуум-гипотеза справедлива. Можно выписать и такую формулу 2-го порядка, наличие у которой модели равносильно, напротив, наличию промежуточной мощности, т. е. справедливости отрицания континуум-гипотезы. Таким образом, для формул 2-го порядка вопрос о наличии у них модели может оказаться столь же туманным, как сама континуум-гипотеза. (Пример формулы, обладающей указанным свойством, интересующийся читатель найдёт в приложении к данной статье.)
Кажется сомнительным, чтобы язык со столь неясной семантикой мог служить удовлетворительным средством для аксиоматического определения чего-нибудь, в частности натурального ряда.
И действительно, если мы проанализируем использование аксиомы индукции в процессе доказательства того, что любая модель аксиом I–III изоморфна N, мы увидим, что здесь, по существу, используется то самое понятие натурального числа, которое мы ещё только собираемся аксиоматически определить. Наше свойство P0 означает «иметь вид 0''…'». Многоточие между штрихами в выражении «0''…'» как раз и пытается заменить собою общее представление о натуральном числе. А выразить свойство Р0 без априорного представления о натуральном числе или без заменяющих его многоточия или слов «и так далее» невозможно.
Назад: 3. Можно ли определить натуральный ряд (с прописной буквы)?
Дальше: 5. «Можно ли доказать, что великую теорему ферма нельзя ни доказать, ни опровергнуть?»

