§ 10. Счётные и несчётные множества

Книга: Апология математики (сборник статей)

Назад: § 9. Задачи из элементарной комбинаторики

Дальше: § 11. Представление о математических доказательствах меняется со временем

Прежде всего не станем уподобляться свифтовским остроконечникам и тупоконечникам, готовым воевать с теми, кто при поедании яиц разбивает их не с того конца. Признаем, что ноль можно считать, а можно и не считать натуральным числом. Потому что на самом деле есть два понятия натурального числа: количественное, возникающее при исследовании количества элементов в множестве, и считательное, возникающее при пересчёте элементов этого множества, при условии, что таковые существуют. Из сказанного ясно, что наименьшее количественное натуральное число есть ноль; это количество элементов в пустом множестве. Наименьшее считательное натуральное число есть единица, потому что с неё начинается любой пересчёт. Сообразно этому есть два натуральных ряда – количественный, начинающийся с ноля, и считательный, начинающийся с единицы. Между ними нетрудно установить взаимно однозначное соответствие:

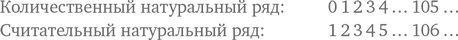
К сожалению, оба натуральных ряда претендуют на обозначение N. Это не слишком страшно, потому что из контекста ясно, какой из двух натуральных рядов имеется в виду. В этом параграфе натуральный ряд начинается с единицы.

Множество называется счётным, если между ним и натуральным рядом можно установить взаимно однозначное соответствие. Например, множество всех целых чисел счётно, как показывает бесконечная таблица из двух строк:

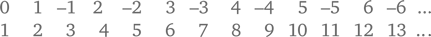
В первой строке в некотором порядке выписаны все целые числа, во второй – соответствующие им члены натурального ряда. Ясно, что между любыми двумя счётными множествами можно установить взаимно однозначное соответствие (хотя бы через промежуточное соответствие каждого из них с натуральным рядом). Поэтому все счётные множества имеют одинаковую мощность или одинаковое количество элементов – столько же, сколько их содержится в натуральном ряду, т. е. столько же, сколько существует натуральных чисел.

Позволительно дать и такое определение счётного множества:

множество называется счётным, если его можно пересчитать, т. е. назвать какой-то его элемент первым; какой-то элемент, отличный от первого, – вторым; какой-то, отличный от первых двух, – третьим и т. д., причём ни один элемент множества не должен быть пропущен при пересчёте.

Как только какое-либо бесконечное множество удалось расположить в последовательность отличных друг от друга элементов, так сразу возникает его взаимно однозначный пересчёт: член последовательности, стоящий на первом месте, и только он, объявляется первым; член, стоящий на втором месте, и только он, – вторым и т. д. Возьмём, к примеру, множество всех слов, составленных из букв a и b, и расположим его в последовательность:

A, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, …, baaba, baabb, ….

Правило расположения слов в последовательности мы выбрали таким (а могли бы выбрать и другим): группируем слова по длине, а в пределах группы располагаем их в алфавитном порядке. Раз множество всех слов в двухбуквенном алфавите удалось расположить в последовательность различающихся элементов, значит, оно счётно. Аналогичным образом можно расположить в последовательность различающихся элементов и множество слов в любом другом алфавите. Поэтому имеет место следующий фундаментальный факт: каков бы ни был алфавит, множество всех слов в этом алфавите счётно.

Пример 42. Доказать, что объединение счётного множества A с конечным множеством B является счётным множеством.

Пусть A = {a₁, a₂, a₃, …, a_n, …} и B = {b₁, b₂, b₃, …, b_n}. Тогда их объединение A ∪ B можно расположить в последовательность {b₁, b₂, b₃, …, b_n, a₁, a₂, a₃, … a_n, …}. Элемент a₁ получит в этой последовательности номер (n + 1). Следовательно, объединение счётного и конечного множеств счётно.

Пример 43. Доказать, что объединение счётного множества A со счётным множеством B является счётным множеством.

Пусть A = {a₁, a₂, a₃, …, a_n, …} и B = {b₁, b₂, b₃, …, b_n, …}. Тогда их объединение A ∪ B можно расположить в последовательность {a₁, b₁, a₂, b₂, a₃, b₃, …, a_n, b_n, …}. Значит, объединение двух счётных множеств счётно.

Пример 44. Доказать, что всякое бесконечное множество M содержит счётное подмножество.

Так как множество M бесконечно, в нём имеется какой-то элемент, который мы обозначим a₁. Бесконечное множество не может исчерпываться этим единственным элементом, поэтому в M присутствует ещё какой-то, отличный от a₁ элемент, который мы обозначим a₂. Но и этими двумя элементами не исчерпывается бесконечное множество, поэтому в нём найдётся элемент a₃, отличающийся как от a₁, так и от a₂. Продолжая процесс, мы выделим из множества M счётное подмножество {a₁, a₂, a₃, …}. Итак, всякое бесконечное множество содержит счётное подмножество.

Когда автор этих строк в 1947 г. пришёл студентом на мехмат Московского университета, он ещё застал замечательное выражение разве что счётное множество, означающее множество, являющееся конечным или счётным. Хотелось бы вдохнуть в него новую жизнь, и потому примеры 45 и 46 мы сформулируем с его использованием.

Пример 45. Доказать, что всякое подмножество разве что счётного множества разве что счётно.

Если объемлющее множество конечно, то всякое его подмножество конечно. Если же оно бесконечно, то расположим его элементы в последовательность β с неповторяющимися членами. Те члены этой последовательности, которые принадлежат интересующему нас подмножеству, естественным образом образуют конечную или бесконечную подпоследовательность последовательности β, что и доказывает, что это подмножество конечно или счётно. Итак, всякое подмножество разве что счётного множества разве что счётно.

Пример 46. Доказать, что объединение М ∪ С бесконечного множества M с разве что счётным множеством C содержит столько же элементов, сколько и M.

Напомним, что через C \ M обозначается множество всех тех элементов С, которые не являются элементами M. Заметим, что М ∪ С = М ∪ Н, где H = C \ M, причём H разве что счётно и не пересекается (т. е. не имеет общих элементов) с M. Если мы сумеем установить взаимно однозначное соответствие между M и М ∪ Н, то провозглашённый в примере 46 факт будет доказан.

Мы поступим так. Множество M разобьём на два непересекающихся множества A и B: M = A ∪ B, а множество М ∪ Н на два непересекающихся множества K и L: М ∪ Н = K ∪ L. Затем установим два взаимно однозначных соответствия: соответствие η между A и K и соответствие θ между B и L. При этом автоматически возникнет соответствие между множеством A ∪ B, равным M, и множеством K ∪ L, равным М ∪ Н, каковое соответствие, в силу того что A не пересекается с B, а K не пересекается с L, будет взаимно однозначным.

Приступаем к осуществлению плана. Выделяем в М счётное подмножество R. Полагаем A = M \ R, B = R, K = M \ R, L = R ∪ Н. В качестве η берём соответствие тождества, при котором каждый элемент соответствует сам себе. Множество R счётно, а множество H конечно или счётно. Поэтому (см. примеры 42 и 43) множество L счётно и между ним и B существует взаимно однозначное соответствие. Одно из таких соответствий берём в качестве θ. Итак, объединение бесконечного множества с разве что счётным множеством содержит столько же элементов, сколько и бесконечное множество.

В § 8 мы уже встретились с примером бесконечного множества, не являющегося счётным. Это было множество Ω всех бесконечных двоичных последовательностей. Множество называется несчётным, если оно бесконечно и не является счётным. Можно было бы сказать и так: множество называется несчётным, если оно не является разве что счётным. Сам факт существования несчётных множеств весьма принципиален, поскольку показывает, что бывают бесконечные множества, количество элементов в которых отлично от количества элементов натурального ряда. Установление данного факта в XIX в. Георгом Кантором является одним из крупнейших открытий в математике.

В этом параграфе будет показано, что некоторые из хорошо известных множеств несчётны. Среди таких множеств – прямая (понимаемая как множество её точек), луч, отрезок и интервал. Напомним, что интервал]a; b[состоит из всех точек, расположенных между точками a и b, тогда как отрезку [a; b], помимо указанных точек, принадлежат ещё и сами точки a и b.

Но прежде всего следует сказать об аксиоме вложенных отрезков. Список аксиом геометрии включает одну или несколько (в зависимости от выбранной версии списка) так называемых аксиом непрерывности, которые обеспечивают непрерывность прямой. Понятно, что данная фраза требует разъяснения. Дадим его в форме иллюстрации.

Допустим, мы должны воткнуть иглу циркуля в точку прямой, заданным раствором описать окружность и найти точку пересечения этой окружности с исходной прямой. Теперь вообразим, что такой точки мы не находим, потому что там, где мы рассчитываем её обнаружить, в прямой дырка. «Но это невозможно!» – с возмущением воскликнет читатель. Однако подобная невозможность как раз и обеспечивается аксиомами непрерывности. Представим себе, что прямая содержала бы только точки с рациональными координатами, а нужная нам точка имела бы координату √2 и потому отсутствовала бы на прямой. Аксиомы непрерывности и гарантируют присутствие на прямой точек с любыми действительными координатами и тем самым возможность отождествления точек прямой с действительными числами, координатами этих точек. Говорят, что точки прямой (или соответствующие им действительные числа) образуют континуум. Латинское прилагательное continuus (это в мужском роде, а в среднем – continuum) как раз и означает 'непрерывный, сплошной, связный, продолжающийся без перерыва, не имеющий ни скачков, ни пробелов'. Можно говорить о континууме точек на интервале или на отрезке, но говорить, скажем, о континууме рациональных точек нельзя.

Известны несколько вариантов аксиомы (или аксиом) непрерывности, из которых мы выберем такой:

Пусть дана бесконечная последовательность вложенных друг в друга отрезков:

[a₁; b₁] ⊃ [a₂; b₂] ⊃ [a₃; b₃] ⊃ … ⊃ [a_n; b_n] ⊃ ….

Существует точка, принадлежащая всем этим отрезкам.

Это и есть аксиома о вложенных отрезках. (Подумайте, почему в формулировке аксиомы нельзя заменить отрезки интервалами.)

Пример 47. Доказать, что множество точек прямой несчётно.

Доказательство ведём от противного. Допустим, что это множество счётно и перенумеруем его: x₁, x₂, x₃, …, x_n, …. Образуем последовательность вложенных отрезков по следующему принципу: отрезок [a_k; b_k] не должен содержать ни одну из точек x₁, x₂, x₃, …, x_k. Тогда не найдётся ни одной точки xn, которая принадлежала бы всем отрезкам, что нарушает аксиому. Итак, множество точек прямой несчётно.

Совершенно так же доказывается несчётность отрезка, интервала, открытого (без вершины) и замкнутого (включая вершину) луча. Каждая из этих геометрических фигур понимается в данном случае как множество своих точек. Более того, все эти множества оказываются равномощными; говорят, что они континуальны или что они имеют мощность континуума. Сейчас мы докажем заявленную равномощность.

Пример 48. Доказать, что все отрезки на числовой прямой равномощны. Достаточно доказать равномощность произвольного отрезка [a; b] единичному отрезку [0; 1] (тогда все отрезки окажутся равномощными в силу принципа транзитивности). Формула y = (1 – t)a + tb, где t пробегает [0; 1], даёт требуемое взаимно однозначное соответствие между [0; 1] и [a; b]. Приводимая формула имеет наглядную физическую интерпретацию: точка y едет с постоянной скоростью от левого конца отрезка [a; b] к правому и достигает цели в течение единичного интервала времени; каждому моменту единичного интервала соответствует положение точки в этот момент. Следовательно, все отрезки на числовой прямой равномощны.

Пример 49. Доказать, что все интервалы равномощны. Доказательство ведётся так же, как в примере 48, только t пробегает теперь не отрезок [0;1], а интервал]0; 1[.

Пример 50. Доказать, что всякий интервал равномощен прямой.

Формула y = tg x устанавливает взаимно однозначное соответствие между интервалом] –π/2; + π/2[и прямой. А все интервалы равномощны друг другу. Следовательно, всякий интервал равномощен прямой.

Пример 51. Доказать, что интервал]a; b[и отрезок [a; b] равномощны.

Записываем [a; b] =]a; b[∪ {a; b} и вспоминаем результат примера 46.

Континуальность лучей просим читателя рассмотреть самостоятельно.

Пример 52. Как доказать, что существуют иррациональные числа?

Можно предложить прямое доказательство существования иррациональных чисел. Например, указать число √2 и доказать, что оно иррационально. Выше были приведены два таких доказательства: арифметическое (в примере 11) и геометрическое (в примере 19). Но можно предложить и косвенное доказательство.

Множество всех рациональных чисел счётно, а множество всех действительных чисел несчётно; значит, бывают и числа, не являющиеся рациональными, т. е. иррациональные. Конечно, надо ещё доказать счётность множества рациональных чисел. Счётность множества рациональных чисел вытекает из того, что каждому рациональному числу можно дать имя в виде слова в едином для всех рациональных чисел алфавите.

Изъяснимся подробнее. В качестве единого алфавита выбираем двенадцатибуквенный алфавит {–; /; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9}. С каждым рациональным числом взаимно однозначно сопоставляем несократимую дробь, а дробь записываем в виде m/n, если она положительна, и в виде – m/n, если она отрицательна; здесь m и n – десятичные записи натуральных чисел. Эту запись m/n или – m/n объявляем именем соответствующего рационального числа. Множество данных имён счётно как подмножество счётного множества всех слов в данном алфавите, а потому счётно и множество всех рациональных чисел.

В примере 52 косвенное доказательство было не намного проще прямого. Но бывают ситуации, когда косвенное доказательство гораздо проще прямого. Именно так обстоит дело в случае трансцендентных чисел.

Действительное число называется алгебраическим, если оно является корнем ненулевого многочлена с целыми коэффициентами; в противном случае оно называется трансцендентным. Прямое доказательство существования трансцендентных чисел состоит в предъявлении образца таких чисел. Первое такое предъявление было осуществлено в 1844 г., чем и было доказано существование трансцендентных чисел. Впоследствии было доказано, что трансцендентными являются известные числа e (основание натуральных логарифмов) и π (отношение длины окружности к диаметру). Однако доказать, что число e или число π (или какое угодно другое число) является трансцендентным, довольно сложно. В то же время возможно следующее несложное косвенное доказательство существования трансцендентных чисел. Надо сравнить два множества – несчётное множество всех действительных чисел и множество всех алгебраических чисел – и убедиться, что второе счётно. Счётность следует из того, что каждое алгебраическое число можно «назвать», т. е. присвоить ему некоторое имя. В качестве такого имени проще всего взять выражение, состоящее из двух частей: 1) из записи соответствующего многочлена и 2) порядкового номера рассматриваемого числа среди корней этого многочлена (корни берутся в порядке возрастания).

Нетрудно придумать алфавит, в котором все эти имена записывались бы в виде слов. Некоторые имена окажутся «пустыми» в том смысле, что не называют никакого числа. Так случится, если уравнение не имеет действительных корней, а также если уравнение имеет, скажем, десять таких корней, а мы включили в имя номер сотого корня. Такие имена мы отбрасываем. У каждого действительного числа окажется много имён, из них мы выбираем то, которое идёт первым в пересчёте всех слов придуманного нами алфавита; остальные имена отбрасываем. Таким образом, множество имён алгебраических чисел окажется подмножеством всех слов в некотором алфавите и, следовательно, счётным. Вместе с ним счётным окажется и множество всех алгебраических чисел. Раз множество всех алгебраических чисел счётно, а множество всех действительных чисел несчётно, то непременно бывают действительные числа, не являющиеся алгебраическими, т. е. трансцендентные.

замечание. И в примере 52, где доказывалось существование чисел, не являющихся рациональными, и в последующем доказательстве существования чисел, не являющихся алгебраическими, была использована следующая идея: множество «выделенных» чисел (рациональных, алгебраических) допускает пересчёт (поскольку оно счётно), а множество всех чисел не допускает пересчёта (поскольку оно несчётно); следовательно, существуют числа, не являющиеся «выделенными». Более рафинированный вариант этой идеи таков. Имеется множество и подмножество, оба допускают пересчёт. Среди пересчётов выделяются пересчёты специального вида и доказывается, что подмножество допускает такой пересчёт, а объемлющее множество не допускает. Тем самым обнаруживается, что в множестве существуют элементы, не принадлежащие подмножеству. Именно такой рафинированный вариант используется в одном из доказательств знаменитой теоремы Гёделя о неполноте. Множество всех истинных утверждений арифметики не допускает вычислимого пересчёта, тогда как множество всех доказуемых утверждений арифметики такой пересчёт допускает. Отсюда следует существование истинных утверждений, не являющихся доказуемыми. Этот способ доказательства теоремы Гёделя предложил великий математик Андрей Николаевич Колмогоров.

Назад: § 9. Задачи из элементарной комбинаторики

Дальше: § 11. Представление о математических доказательствах меняется со временем