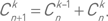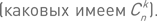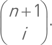§ 9. Задачи из элементарной комбинаторики

Выражение (читается «цэ из n по k») означает количество k-элементных частей n-элементного множества или, в более современной терминологии, количество частей мощности k множества мощности n.

Пример 37. Доказать равенство

Пусть множество M имеет n элементов. Каждому его подмножеству A мощности k взаимно однозначно соответствует его дополнение M \ A, состоящее в точности из тех (n – k) элементов, которые не входят в A. Наличие этого взаимно однозначного соответствия и доказывает равенство.

Пример 38. Доказать равенство

Равенство очевидно, если вспомнить, что количество частей n элементного множества равно 2ⁿ (см. пример 33).

Равенство (*) из примера 39 не столь очевидно.

Пример 39. Доказать равенство

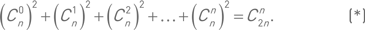
Постараемся доказать равенство (*) как можно нагляднее. Возьмём множество M, имеющее 2n элементов, произвольно отберём из него n элементов и назовём их «белыми»; остальные n элементов назовём «чёрными». Каждое подмножество K множества M, содержащее n элементов, есть объединение двух частей – «белой» части A, состоящей только из «белых» элементов, и «чёрной» части B, состоящей только из «чёрных» элементов: K = A ∪ B. Число элементов в каждой из этих частей может варьироваться от 0 до n. Приготовим n + 1 «комнату», на которых выставим номера от 0 до n. Все подмножества мощности n множества M распределим по этим «комнатам», соблюдая следующее правило: в «комнату» с номером k помещаются те подмножества, число «белых» элементов в которых равно k. В каждой «комнате» поставим «столов» и подмножества, попавшие в эту «комнату», распределим по этим «столам». Число «белых» подмножеств мощности k множества M, т. е. подмножеств, содержащих k «белых» элементов и ноль «чёрных», равно т. е. числу «столов». Для каждого такого «белого» подмножества взаимно однозначно выберем свой «стол». На этом «столе» располагаются подмножества мощности n множества M, у которых «белая» часть уже фиксирована, а «чёрная» часть варьируется. «Белая» часть имеет мощность k. «Чёрной» частью может быть любое множество мощности (n – k), элементы которого выбраны из n «чёрных» элементов, присутствующих в M. Так что для заданного стола число возможных «чёрных» частей есть Столько же подмножеств множества M лежит на нашем «столе». Итак, в «комнате» «столов», а на каждом из них подмножеств. Значит, в «комнате» подмножеств. Осталось вспомнить равенство из примера 37 и сложить количества подмножеств по всем «комнатам», чтобы получить общее количество n элементных подмножеств множества M в виде левой части равенства (*). А в правой части стоит символ, по определению выражающий это количество.

Пример 40. Доказать равенство

В множестве мощности (n + 1) выделим какой-то элемент. Совокупность k элементных подмножеств этого множества распадается на два класса: содержащих элемент и не содержащих выделенного элемента

Пример 41. Доказать равенство

Для доказательства полезно привлечь так называемые биномиальные коэффициенты.

Биномиальные коэффициенты – это коэффициенты разложения бинома (1 + x)ⁿ по возрастающим степеням x:

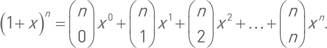
Из выписанной формулы видно, как они обозначаются. Если в этой формуле положить x = –1, то получим:

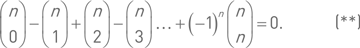
Только что полученная формула очень похожа на равенство, которое требовалось доказать. И это не случайно. Дело в том, что биномиальный коэффициент и количество подмножеств  – это одно и то же число.

Пример 42. Доказать равенство

Мы наметим лишь план доказательства. Сначала равенство проверяется для случаев k = 0 и k = n. Затем доказывается равенство, аналогичное равенству из примера 40:

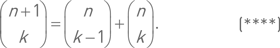
Доказать это равенство чрезвычайно просто. Надо рассмотреть два способа записи разложения степени бинома (1 + x)n+1 по возрастающим степеням x. Первый способ – стандартный, с использованием коэффициентов

Второй способ таков: возводим (1 + x) в степень n, располагаем по степеням x с использованием коэффициентов а затем это разложение умножаем на (1 + x) и развёртываем в многочлен. Если теперь приравнять коэффициенты при одинаковых степенях переменной, то получим равенство (****). Далее, для получения равенства (***) рассуждаем по индукции.

Этому рассуждению можно придать легко запоминающуюся форму. Рассмотрим так называемый треугольник Паскаля:

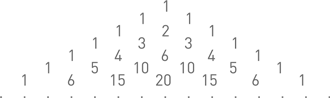
По краям стоят единицы, а каждое другое число равно сумме двух его «соседей» из предыдущей строки. Таблица неограниченно продолжается вниз. Занумеруем строки, считая верхнюю строку (из одной единицы) нулевой. Таким образом, первая строка – это 11, вторая – 121 и т. д. Аналогично нумеруем числа в каждой строке: самая левая единица получает номер ноль, за ней следует число номер один и т. д. Например, третье число в шестой строке – это 20.

Наше доказательство равенства можно теперь сформулировать так: числа равны потому, что каждое из них есть k-е число в n-й строке треугольника Паскаля.

Отправить