Великий французский математик Анри Пуанкаре писал в 1908 г.:

Для иллюстрации приведём рассуждение из книги «Введение в анализ бесконечных». Правда, она была опубликована в 1748 г., т. е. не за 50, а за 160 лет до высказывания Пуанкаре, зато сам пример очень нагляден. В названной книге встречаются такие странные, по нынешним меркам, утверждения: «e^x = (1 + x/i)ⁱ, где i означает бесконечно большое число»; «так как дуга 2kπ/i бесконечно мала, то cos(2k/i) π = 1 – (2k²/i²)π²»; «член x²/i² может быть опущен без опасения, потому что даже после умножения на i он останется бесконечно малым». Скажи студент такое на экзамене в наши дни, он получил бы двойку. Однако автор книги не кто иной, как великий математик Эйлер, а взятые нами в кавычки цитаты составляют часть доказательства одной из знаменитых формул Эйлера, а именно формулы для разложения синуса в бесконечное произведение:

Формула Эйлера и поныне составляет одну из жемчужин математического анализа. В середине XX в. даже выяснилось, что и процитированным «странным» утверждениям Эйлера можно придать точный смысл на основе так называемого нестандартного анализа, но это уже совсем другая история.

Мы видим, таким образом, что само понимание того, что является, а что не является доказательством, меняется со временем. Если вдуматься, ничего удивительного в этом нет. Ведь понятие доказательства основано на представлении об убедительности, а это представление исторически обусловлено. Для средневековых судов, например, убедительными были весьма своеобразные, с нашей точки зрения, доказательства виновности и невиновности: если человек мог держать в руке раскалённое железо, то он признавался невиновным; если брошенная в воду связанная женщина не тонула, то её объявляли ведьмой. Понятие математического доказательства имеет те же психологические основы, что и понятие доказательства юридического, и потому так же зависимо от исторических обстоятельств.

Для математических текстов средневековой Индии, например, были характерны такие (возможно, восходящие к более древним временам) способы доказывания геометрических утверждений: предлагался чертёж, под которым стояло всего одно слово «Cмотри!». На рис. 4 воспроизведено подобное индийское доказательство формулы, выражающей площадь круга S через длину окружности l и радиус r. Формула эта замечательна тем, что не использует числа π, осознание которого в качестве полноправного числа сталкивается с вполне естественными психологическими трудностями, ведь оно не представимо ни в виде дроби, ни даже в виде выражения с радикалами (т. е. знаками корня), как это имеет место в случае диагонали единичного квадрата. Поэтому данная формула могла быть понятна и в древности. Найти её нетрудно. Поскольку l = 2πr, то в известной формуле площади круга число π можно заменить отношением длины полуокружности к радиусу:

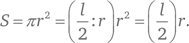
Таким образом, площадь круга равна площади прямоугольника, основанием которого служит отрезок, равный по длине полуокружности этого круга, а высотой – его радиус. Именно это наглядно показывает индийский чертёж, одновременно демонстрируя и доказательство. Сперва круг делится диаметром пополам, а потом каждый полукруг разрезается на большое и одинаковое для каждого полукруга количество равных секторов. Затем каждая из полуокружностей распрямляется, секторы превращаются в треугольники, и возникают две равные фигуры, по форме напоминающие пилу. Наконец, эти «пилы» вставляются друг в друга, так чтобы зубцы одной «пилы» полностью вошли в промежутки между «зубцами» другой. Возникает прямоугольник, равный по площади исходному кругу и имеющий требуемые длины сторон. «Что за чушь?! – скажет педант XXI в. – При распрямлении дуг секторы превратятся бог знает во что и не смогут совпасть с промежутками между "зубцами", да и площади их исказятся. И прямоугольник выйдет кривобокий. Так что никакое это не доказательство». Однако для индийцев это было доказательством. И минувшие века не лишили его убедительности, ведь при разбиении на очень большое количество секторов все справедливо отмеченные педантом искажения будут почти незаметны. Так что при большом желании и готовности потрудиться индийское рассуждение можно облечь в форму, приемлемую сегодня.

Для полноты картины приведём индийское доказательство теоремы Пифагора. Это тоже чертёж со словом «Смотри!». Заметим, что

Поэтому теорему Пифагора, утверждающую, что для прямоугольного треугольника с катетами a и b и гипотенузой c справедливо равенство a² + b² = c², можно доказывать в форме

Последняя формула и доказывается чертежом, приведенным на рис. 5. Слева на рис. 5 – квадрат с площадью c², составленный из четырёх одинаковых треугольников и квадрата со стороной a − b. Справа – тот же квадрат со стороной a – b, а треугольники уложены так, что образовались два одинаковых прямоугольника со сторонами a и b. Заметим, что, в отличие от предыдущего, это рассуждение полностью приемлемо и сегодня.

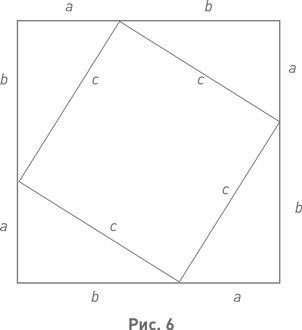
Наш рис. 5 с подписью «Смотри!» встречается в трудах индийского астронома и математика XII в. Бхáскары. Можно предположить, что он содержался в ещё более ранних индийских текстах. В пользу такого предположения говорит, в частности, то, что левый чертёж с рис. 5 мы находим в китайском трактате, датируемом не позже чем III в. Китайский автор, однако, не довольствуется призывом «Смотри!», а заменяет его алгебраическим пояснением. В упомянутом трактате предлагалось и другое, пожалуй, ещё более простое и наглядное доказательство теоремы Пифагора. Это второе доказательство иллюстрирует рис. 6. Китайский автор и в этом случае сопровождал чертёж необходимым пояснением; мы же на индийский манер ограничимся призывом «Смотри!». Для точности укажем, что китайский чертёж состоял из наложенных друг на друга чертежей, показанных на рис. 5 и 6, давая таким образом одновременно два доказательства теоремы Пифагора.

В древних египетских текстах описываются приёмы оперирования с простыми дробями – не со всеми, а с некоторыми избранными: аликвотными (так принято называть дроби с числителем единица) и дробью 2/3. Встречаются также способы вычисления простейших площадей. Но все они приводятся без какого бы то ни было обоснования. По-видимому, в то время в нём не ощущалось психологической необходимости. Убедительность способа проистекала из того, что он, во-первых, исходил из авторитетного источника (как правило, от жреца) и, во-вторых, был записан. (Не так ли подчас и мы относимся к медицинским предписаниям?) Жившие в советское время помнят, что любое утверждение считалось полностью доказанным, коль скоро его удавалось обнаружить в каком-либо из текстов Маркса или Ленина; в сталинское же время ещё более неоспоримыми были тексты Сталина. (Так что официальная ментальность того времени недалеко ушла от ментальности Древнего Египта.)

Первые математические доказательства в современном их понимании приписывают древнегреческим мыслителям Фалéсу и Пифагору. Считается, что именно в Древней Греции в VII–VI вв. до н. э. возник новый, до того не встречавшийся обычай сопровождать математический факт его обоснованием. Появилась потребность не просто сообщать факт, но и убеждать слушателя в его истинности, т. е. проводить доказательство. По-видимому, сама идея необходимости убеждать слушателей появилась в дискуссиях на народных собраниях и в судах. (В этом смысле математика – младшая сестра юриспруденции.)

Древнегреческие доказательства были почти безупречны с современной точки зрения. Положение вещей начало меняться с XVII в., когда в математику вошли переменные величины, а вместе с ними представление о предельном переходе. С сегодняшней точки зрения эти понятия и представления не были достаточно чёткими, а потому и относящиеся к ним доказательства XVII–XVIII вв. кажутся теперь нестрогими, вспомним хотя бы приведённые выше цитаты из книги Эйлера. Замечательно, однако, что эти нестрогие доказательства приводили к строгим результатам, прочно вошедшим в арсенал современной математики. Так продолжалось до 20-х гг. XIX в., когда появились работы знаменитого французского математика Луи Огюстена Коши; в его трудах понятие предела и опирающиеся на него понятия впервые стали приобретать ту логическую форму, которую они имеют сегодня. Инициатива Коши была развита затем многими математиками, прежде всего уже во второй половине XIX в. знаменитым немецким математиком Карлом Вейерштрассом. Но новые представления о необходимом уровне математической строгости входили в математику не сразу, о чём свидетельствует открывающее этот раздел высказывание Пуанкаре. Напрашивается предположение, что представления о строгости будут развиваться и впредь и то, что кажется строгим сегодня, не покажется таковым в будущем.

Уже сейчас видно одно из направлений, по которым может развиваться пересмотр представлений об убедительности математических доказательств. Дело в том, что само понимание того, что такое математическая истина, вызывает серьёзные затруднения. Ведь математические объекты, в отличие от объектов физических, не присутствуют в природе, они существуют лишь в умах людей. Поэтому в применении к математическим истинам говорить, что истина – это то, что соответствует реальному положению вещей, можно лишь с большой натяжкой.

Чтобы закончить этот раздел на оптимистической ноте, подчеркнём, что доказательства, содержащиеся в трудах Евклида и Архимеда, не потеряли своей убедительности за прошедшие тысячи лет.