Продолжим наши попытки разъяснить формулировку гипотезы Пуанкаре. С этой целью прежде всего напомним эту формулировку: всякое односвязное трёхмерное компактное многообразие без края гомеоморфно трёхмерной сфере.

«Да что же это такое?! – в сердцах воскликнет читатель. – Автор не удосужился даже перечитать ту формулировку, которую сам же привёл в конце главы 9! Ведь там не было слов "без края"!» Действительно, не было. Дело в том, что математическая терминология точна, но, к сожалению, не однозначна: один и тот же термин подчас употребляется, увы, в разных смыслах. (Мы уже столкнулись с неоднозначностью термина «натуральное число»: при одном понимании число ноль считается натуральным, при другом – нет.) В применении к многообразиям в ходу две терминологические системы. Первая допускает, что многообразия могут как иметь край, так и не иметь его; в её рамках противопоставляются многообразия с краем и многообразия без края, и те и другие называются многообразиями. Вторая система называет многообразиями только те объекты, которые в первой системе именуются многообразиями без края; в рамках этой системы многообразия противопоставляются многообразиям с краем; в этой второй терминологии термин «многообразие с краем» надлежит рассматривать как словосочетание неделимое, а не как означающее такое многообразие, которое имеет край. Дабы сделать формулировку более короткой, в главе 9 мы использовали вторую терминологическую систему. В данной главе нам встретятся многообразия с краем, и, чтобы читатель не запутался, мы будем использовать более контрастную первую систему.

В приведённой только что формулировке выделим понятия, разъяснения коих сделает формулировку понятной. Понятие компактного многообразия без края естественно расщепляется на два: 'компактное многообразие' и 'многообразие без края'. Тогда возникают пять понятий: 'односвязное', 'компактное многообразие', 'многообразие без края', 'гомеоморфно', 'трёхмерная сфера'.

Что такое трёхмерная сфера, мы, как могли, объяснили в предыдущей главе. Самым простым из тех четырёх понятий, которые ещё осталось разъяснить, является понятие односвязности. С него мы и начнём.

Представим себе резинку, которую продают под названием «банковская» и одни называют канцелярской, другие аптечной, т. е. резиновую нить со склеенными концами; при покупке небольшого числа мелких предметов, скажем, карандашей в магазине канцелярских принадлежностей или конвалют (пластиковых матриц с ячейками для таблеток или пилюль) в аптеке, ею часто скрепляют покупку. Вообразим резинку столь упругой, что она, если её не удерживать, стремится стянуться в точку, и столь умной, что ради стягивания в точку она готова пойти и на растяжение: например, если натянуть резинку на «талию» песочных часов, она, чтобы сжаться в точку на вершине колбы, вынуждена будет растянуться, проходя через верхнюю половину колбы. Геометрическая фигура называется односвязной, коль скоро расположенная в её пределах резинка при любом своём расположении (!) имеет возможность беспрепятственно стянуться в точку, не выходя за пределы рассматриваемой фигуры. Поясним сказанное на примерах. Круг односвязен, но, если в нём проделать дыру, он перестанет быть односвязным. Конечно, и в случае круга с дырой можно так разместить в нём резинку, чтобы ничто не препятствовало её стягиванию в точку. Но если мы обведём резинку вокруг дыры, то стянуть её в точку окажется невозможным: дыра помешает. А для односвязности нужно, чтобы стягивание в точку было возможным при любом расположении резинки.

Поверхность стола и поверхность глобуса односвязны, а поверхность большинства современных унитазных сидений, поверхность спасательного круга и боковая поверхность цилиндра не односвязны. Шар и цилиндр односвязны, а бублик – нет; не односвязен и крендель. Говоря об односвязности пространственных тел, мы делаем несколько фантастическое допущение, что резинка вольна свободно перемещаться в толще тела (в наших примерах – в мякише бублика или кренделя). Рекомендуем читателю обнаружить такие расположения резинки внутри бублика, а также на поверхности унитазного сиденья, поверхности спасательного круга и боковой поверхности цилиндра, при которых резинка не может стянуться в точку, не покидая названных фигур. Вопрос к читателю: односвязно или нет тело, представляющее собою 1) шар, в котором имеется полость, 2) чашку с ручкой и 3) чашку с отбитой ручкой? Можно доказать, что трёхмерная сфера односвязна.

Наш очерк не претендует на математическую строгость, поэтому определения односвязности в терминах стягивающейся резинки вполне достаточно для наших целей. Тем не менее читатель вправе знать, что такое определение не может считаться математически точным.

Наша следующая тема – многообразия, в частности компактные. Многообразия представляют собою важнейший класс топологических пространств, и, чтобы правильно и полно определить понятие многообразия, следовало бы сначала определиться с тем, что такое топологическое пространство и что такое гомеоморфизм. Иными словами, начать с вводного курса топологии. По понятным причинам делать этого мы не будем, а скрепя сердце пожертвуем и общностью, и точностью. Мы ограничимся рассмотрением многообразий, которые являются геометрическими фигурами. А геометрическая фигура всегда располагается в каком-то из евклидовых пространств, являясь подмножеством точек этого пространства. Такое ограничение, казалось бы, сужает понимание и проблемы Пуанкаре, и результата Перельмана, но на самом деле сужает только формально, поскольку каждое компактное многообразие в общем топологическом смысле этого термина гомеоморфно некоторой геометрической фигуре. Слово «гомеоморфно» будет разъяснено ниже, а некоторые детали прояснятся в конце этой главы.

Отличительным свойством многообразия без края является его локальная однородность: вблизи любой своей точки оно устроено так же, как вблизи другой. Если вырезать из такого многообразия два кусочка в разных местах, то эти кусочки в некотором глубоком смысле нельзя отличить один от другого. Окружность, сфера, прямая, плоскость, трёхмерное пространство – вот наглядные примеры многообразий без края. Край нарушает указанную однородность. Например, у шара краем является ограничивающая его сфера; и кусочек шара, содержащий хотя бы одну точку этой сферы, резко отличается от кусочков того же шара, таких точек не содержащих. Точки геометрической фигуры, принадлежащие её краю, называются краевыми.

В многообразии окрестности всех точек, за исключением краевых, устроены одинаково. При этом под окрестностью какой-либо точки A понимается совокупность всех точек, расположенных вблизи от этой точки A. Конечно, и слово «вблизи», и словосочетание «устроены одинаково» нуждаются в уточнении, без какового тем не менее мы их пока оставляем. Заметим лишь, что мы имеем в виду качественное устройство без учета размеров; с такого рода устройством мы встречались в предыдущей главе, когда говорили о геометрии положения. Точки, не являющиеся краевыми, называются внутренними. Повторим: многообразие вокруг каждой из его внутренних точек устроено так же, как и вокруг любой другой внутренней точки. Микроскопическое существо, находящееся в одной из внутренних точек и способное видеть только ближайшие к нему точки этого многообразия, не в состоянии определить, в какой именно точке оно, существо, находится: вокруг себя оно всегда видит одно и то же.

Многообразия могут иметь любую размерность. Примером одномерной фигуры, не являющейся многообразием, может служить линия в форме буквы Т. Край этой линии состоит из трёх точек: одна точка – в самом низу и две – вверху, в концах «перекладины». Как ни понимай смысл слова «вблизи», окрестностью любой из этих краевых точек будет отрезок с концом в рассматриваемой точке. Окрестностью любой из остальных точек, кроме одной, служит отрезок, содержащий данную точку между своими концами. Но есть здесь и особая точка, окрестность которой не похожа на окрестности других точек. Это та точка, в которой «вертикальная палочка» утыкается в «перекладину»; в этой точке образуется то, что на языке дорожного движения называется Т-образным перекрёстком. Именно поэтому линия в форме буквы Т не является многообразием. Другой пример одномерного немногообразия – линия в форме восьмёрки; в особой точке здесь сходятся четыре линии; краевых точек тут нет. Не является многообразием и одномерная фигура, составленная из двух пересекающихся (или же касающихся друг друга, так что возникает восьмёрка) окружностей; здесь особыми будут точки пересечения (или точка касания).

Чтобы читатель лучше усвоил понятие многообразия, приведём ещё два примера геометрических фигур, многообразиями не являющихся. Физические прообразы их – две детские игрушки: воздушный шарик с удерживающей его нитью и ватно-поролоновый шарик с прикреплённой к нему резинкой; на геометрическом языке это двумерная сфера с приклеенной линией и шар с приклеенной линией. Точки, где происходит приклеивание, – особые. Сфера вместе с пересекающей её плоскостью не является многообразием, поскольку та окружность, по которой происходит пересечение, сплошь состоит из особых точек.

В силу сказанного многообразие без края – это геометрическая фигура, целиком состоящая из внутренних точек. Надеемся, что читатель не забыл ещё разницу между отрезком и интервалом, которой обучают в школе. Отрезок имеет два конца, он состоит из этих концов и всех точек, расположенных между ними. Интервал же состоит только из всех тех точек, которые расположены между его концами, сами же концы в интервал не входят; можно сказать, что интервал – это отрезок с удалёнными концами, а отрезок – это интервал с добавленными к нему концами. Ещё бывают полуинтервалы: полуинтервал – это интервал, в который добавлен один из его концов (иначе говоря, отрезок, у которого удалён один из его концов). Прямая, интервал, отрезок, полуинтервал, окружность служат примерами одномерных многообразий, причём прямая, интервал и окружность суть многообразия без края, а отрезок и полуинтервал – многообразие с краем; край в случае отрезка состоит из двух концов, а в случае полуинтервала – из одного.

Плоскость, сфера, поверхность спасательного круга служат примерами двумерных многообразий без края. Плоскость с вырезанной в ней дырой также будет многообразием, а вот с краем или без края – зависит от того, куда мы относим контур дыры. Отнеся его к дыре, получим многообразие без края; если оставим контур на плоскости, получим многообразие с краем, каковым и будет служить этот контур. Разумеется, мы имели здесь в виду идеальное математическое вырезание, а при реальном физическом вырезании, скажем, вырезании дыры ножницами в листе бумаги, вопрос, куда относится контур, не имеет никакого смысла.

Несколько слов о трёхмерных многообразиях. Шар вместе со сферой, служащей его поверхностью, представляет собою многообразие с краем; указанная сфера как раз и является этим краем. Если мы удалим этот шар из окружающего пространства, получим многообразие без края. Если мы сдерём с шара его поверхность, получится то, что на математическом жаргоне называется «ошкуренный шар», а в научном языке, как нам уже известно из предыдущей главы, – открытый шар. Если удалить открытый шар из окружающего пространства, получится многообразие с краем, и краем будет служить та самая сфера, которую мы содрали с шара. Баранка вместе с корочкой есть трёхмерное многообразие с краем, а если отодрать корочку (которую мы трактуем как бесконечно тонкую, т. е. как поверхность), получим многообразие без края в виде «ошкуренной баранки». Всё пространство в целом – то трёхмерное евклидово пространство, которое известно нам из средней школы, – есть трёхмерное многообразие без края.

Настало время попытаться определить, что такое компактное многообразие. Для большей наглядности мы начнём с двумерных многообразий, от коих сперва спустимся к одномерным, а потом поднимемся до трёхмерных. Двумерное компактное многообразие – это такая поверхность, которую можно сшить из конечного числа лоскутов. Например, простыня, если трактовать её как поверхность, представляет собой двумерное компактное многообразие с краем. Дырявая от ветхости простыня остаётся двумерным компактным многообразием с краем; край этого многообразия состоит из точек, расположенных как по старым, до появления дыр, краям простыни, так и по краям дыр. Лоскутных простыней мне видеть не довелось, а вот лоскутные одеяла я видел. Они представляют собою сшитый из лоскутов чехол, набитый утеплителем, обычно ватой или пухом. Чехол лоскутного одеяла, до того как он набит и зашит, является двумерным компактным многообразием с краем. А вот если его зашить, но не простёгивать, он становится двумерным компактным многообразием без края (если же простегать, он перестаёт быть многообразием, поскольку все точки стежков – особые). Повторим определение: двумерное компактное многообразие – это поверхность, которую можно сшить из конечного количества лоскутов. Слова о конечном количестве кажутся ненужными. Какой смысл говорить о бесконечном количестве лоскутов? Необходимость противопоставления конечного и бесконечного количеств будет вскоре объяснена. Пока что заметим, что математики предпочитают употреблять глагол «склеивать», а не «сшивать». Поэтому можно сказать и так: двумерное компактное многообразие – это поверхность, которую можно склеить из конечного количества лоскутов. Под лоскутом же следует понимать любую поверхность, которую можно получить из замкнутого круга, изгибая, комкая, растягивая и сжимая его как угодно, но только не разрывая и не склеивая с самим собой. С понятием лоскута (но не с термином) мы уже встречались в главе 10, в разделе о геометрии положения, когда говорили о граничащих друг с другом областях. То, что мы называли областью в главе 10, и то, что мы называем лоскутом сейчас, – одно и то же.

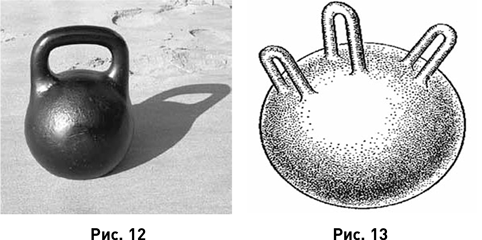
Стандартный футбольный мяч, как известно, склеен (или сшит?) из 32 лоскутов. Что ещё можно склеить из лоскутов? Боковую поверхность цилиндра – это будет многообразие с краем. Но можно склеить и спасательный круг, т. е. на математическом языке – поверхность тора; эта поверхность края не имеет. Поверхность спортивной гири (рис. 12) даёт ещё один пример двумерного компактного многообразия без края.

Можно представить себе гирю настолько тяжёлую, что один человек её не поднимет, самое меньшее – два силача. Тогда к ней следует приделать не одну, а две ручки. Легко представить и гирю, неясно для чего нужную, с тремя ручками (рис. 13), с четырьмя (для четырёх силачей) и вообще с любым числом ручек. Поверхность каждой из таких гирь является двумерным компактным многообразием без края. (Сами же гири суть трёхмерные многообразия с краем.)

Круг является, конечно же, компактным многообразием, но с краем, каковым является ограничивающая круг окружность. Отдерём эту окружность от круга (разумеется, это можно проделать только мысленно). Получится фигура, которая в предыдущей главе была названа открытым кругом. Открытый круг не имеет края, но зато и не является компактным многообразием: его нельзя составить из конечного числа лоскутов. Читатель, верно, уже понял, что такое открытый квадрат – это квадрат без своего периметра. Как и открытый круг, он не является компактным многообразием.

В случае одномерных многообразий роль лоскутов выполняют куски нити. Желая придумать какой-нибудь термин, аналогичный термину «лоскут», мы оказались не способны найти что-либо более удачное, чем слово «обрывок». На языке геометрии обрывок – это линия, которую можно получить из отрезка деформацией, подобной той, с помощью которой мы получали лоскут из круга. Иными словами, обрывок – это то, что можно получить из отрезка, как угодно его изгибая, растягивая и сжимая; запрещаются только разрывы и склеивания. Одномерным компактным многообразием называется всякая линия, которую можно склеить из конечного числа обрывков. При этом подразумевается, что обрывки склеиваются своими концами: конец одного обрывка или не склеивается ни с чем (и тогда возникает край многообразия), или же склеивается с ровно одним концом ровно одного другого обрывка. При таком способе склеивания букву Т, которая служила для нас первым примером немногообразия, получить никак невозможно: при попытке склеить эту букву мы вынуждены будем в особой точке либо склеить один из обрывков с внутренней точкой другого, либо склеить концами сразу три обрывка. Нельзя получить и линию в форме восьмёрки. (При склеивании из лоскутов двумерных многообразий подразумевалось, что лоскуты склеиваются своими краями.) Примерами одномерных компактных многообразий могут служить отрезок и окружность, а также всё, что можно получить из этих фигур, деформируя их как угодно, но только без разрывов и склеиваний. Отрезок, а также всякая линия, которая может быть получена из него деформацией (например, конечный участок любого из тех графиков функций, которые проходят в школе), является одномерным компактным многообразием с краем. Окружность, а также всякая линия, которая может быть получена из неё деформацией (например, обе линии на рис. 14), являются одномерными компактными многообразиями без края. Других примеров одномерных компактных многообразий не существует. (Ни интервал, ни полуинтервал не являются компактными многообразиями.)

Можно ли склеить из обрывков прямую? Можно, но для этого потребуется бесконечное число обрывков. Склеить прямую из конечного числа обрывков невозможно; в силу ранее сказанного это значит, что прямая не компактна. Аналогично плоскость можно склеить из бесконечного числа лоскутов, но нельзя – из конечного; это значит, что плоскость не компактна. Покажем, как из бесконечного числа обрывков можно склеить полуинтервал. Возьмём прямую и будем строить на ней бесконечное число отрезков. Начнём с произвольного отрезка А₀А₁. Пусть его длина равна l. К концу А₁ этого отрезка приклеим отрезок А₁А₂ длины l/2. К точке А₂ приклеим отрезок А₂А₃ длины l/4. И будем подклеивать всё новые и новые отрезки, причём так, чтобы длина каждого отрезка составляла половину длины предыдущего. Из всех этих отрезков, число коих бесконечно, составится полуинтервал длины l + l/2 + l/4 + l/8 +… = 2l с концом в А₀. А если ещё тем же способом подклеивать отрезки с другой стороны исходного отрезка, получится интервал. Надеемся, что читатель сумеет склеить из бесконечного количества лоскутов как открытый круг, так и открытый квадрат.

Мы в состоянии теперь дать общее определение одномерных или двумерных многообразий безотносительно к тому, являются они компактными или нет. Многообразие – это такая геометрическая фигура, которую можно склеить из конечного или бесконечного числа лоскутов (тогда многообразие двумерно) или обрывков (тогда многообразие одномерно).

Призываем читателя, прежде чем двигаться дальше, подумать, как следует определить трёхмерное многообразие.

Сперва надо указать те элементарные «кирпичики», из которых складывается любое трёхмерное многообразие. В случае двумерных многообразий такими «кирпичиками» были лоскуты, в случае одномерных многообразий – обрывки. Чтобы выдержать единство стиля, трёхмерные кирпичики мы назовём комками. Комок – это тело, которое можно получить из шара путём его деформации; при этом шар разрешается мять, растягивать и сжимать, но не разрешается делать склейки и разрывы. Вот пример запрещённой деформации: скатаем шар в цилиндр, а концы цилиндра склеим; мы получим тор, который комком не является. Трёхмерное многообразие – эта такая геометрическая фигура, которая может быть получена склеиванием конечного или бесконечного числа комков. Для склеивания шара, тора, гири с ручками достаточно конечного числа комков; поэтому все эти фигуры суть компактные многообразия. А вот ошкуренный шар или всё пространство можно склеить лишь из бесконечного количества комков, поэтому эти многообразия не являются компактными.

Однако мы обязаны предупредить читателя вот о чём: в главе 12 мы встретимся с компактным двумерным многообразием (а именно бутылкой Клейна), не умещающимся в трёхмерном евклидовом пространстве. Чтобы склеить его из лоскутов, надо выйти из трёхмерного пространства в четырёхмерное. Трёхмерная сфера, являющаяся компактным многообразием, не помещается в трёхмерном пространстве. Чтобы склеить её из комков, также надо выйти в четырёхмерное пространство. А бывают и такие трёхмерные многообразия, для которых не хватает и четырёхмерного пространства, и они требуют для своего размещения пространства пятимерного (слава богу, для размещения трёхмерных многообразий не требуется привлечения пространств с числом измерений, бóльшим пяти). Все наши операции по склеиванию многообразий из обрывков, лоскутов, комков и т. д. были чисто мысленными, а тут, как видим, ещё прибавилась трудность, которая весьма и весьма напрягает мысль, – необходимость для некоторых многообразий выходить в пространства высоких измерений.

Слово «гомеоморфия» пугает непосвященного, но скрывающееся за ним понятие весьма естественно. Предварим разъяснения философическими комментариями. Не могу вспомнить, у кого я вычитал следующую мудрую сентенцию: наука начинается там, где устанавливаются понятия одинаковости и различия. Когда эти понятия установлены, то определяется и совокупность тех свойств, которые являются общими у одинаковых предметов. Именно изучение этих общих свойств, каковые естественно назвать инвариантами, составляет основу того или иного раздела науки.

Проиллюстрируем сказанное примером из зоологии. В самом элементарном смысле каждая собака одинакова только сама с собой, но уже на следующей ступеньке абстракции одинаковы все таксы и все сенбернары. (Кинологи меня убьют, справедливо заявив, что таксы – это целая группа пород, а сенбернары бывают двух разновидностей – длинношёрстные и короткошёрстные, так что предложенная ступенька не является следующей.) Затем можно считать, что одинаковы все собаки, отличая их, однако, от волков и лисиц. Далее можно и собак, и волков, и лисиц признать одинаковыми, как представителей семейства псовых (они же собачьи, они же волчьи). И так вплоть до одинаковости всех живых организмов. Этот пример показывает, что чем более либерально представление об одинаковости, чем меньше объём тех свойств, которые должны совпасть у двух предметов для признания их одинаковыми, тем важнее и глубже становится само понятие одинаковости, ведь очевидно, что различие между собакой и камнем важнее и глубже различия между собакой и кошкой. Инварианты, присущие всем живым организмам, и составляют основной предмет изучения биологии.

Уже в школьной геометрии мы встречаемся с двумя видами одинаковости – конгруэнтностью фигур и их подобием. Как мы уже говорили, в школе конгруэнтные фигуры как бы не различают и потому называют их равными. Конгруэнтные фигуры имеют одинаковые размеры во всех своих деталях (т. е. изометричны). Подобие же, не требуя одинаковости размеров, означает одинаковость пропорций этих размеров; поэтому подобие отражает более сущностное сходство фигур, нежели конгруэнтность. (А изометрия занимает промежуточное, хотя и очень близкое к конгруэнтности, положение между конгруэнтностью и подобием.)

Гомеоморфия – это наиболее глубокая степень геометрической одинаковости. Сейчас мы попытаемся дать приблизительное объяснение этому понятию путём постепенного к нему приближения.

Геометрия в целом стоит на более высокой ступени абстракции, нежели физика, а физика – чем материаловедение. Возьмём, к примеру, шарик подшипника, бильярдный шар, крокетный шар и мяч. Физика не вникает в такие детали, как материал, из которого они сделаны, а интересуется лишь такими свойствами, как объём, вес, электропроводность и т. п. Для математики все они шары, различающиеся только размерами. Если шары имеют разные размеры, то они различаются для метрической геометрии, но одинаковы для геометрии подобия. Поэтому геометрия подобия более абстрактна, чем метрическая геометрия. С точки зрения геометрии подобия одинаковы и все шары, и все кубы, а вот шар и куб не одинаковы. Метрическая геометрия изучает те инварианты, те свойства, которые являются общими для всех конгруэнтных друг другу фигур, а геометрия подобия – те инварианты, которые являются общими для всех фигур друг другу подобных.

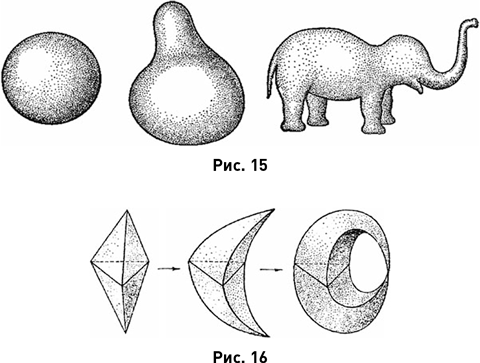
А теперь посмотрим на тор. Призываем благосклонного читателя осознать, что шар и куб «более одинаковы» между собой, чем каждый из них и тор. Наполнить это интуитивное осознание точным смыслом позволяет следующий мысленный эксперимент. Представим себе трёхмерную геометрическую фигуру (тело) сделанной из материала столь податливого, что его можно изгибать, растягивать, сжимать и вообще деформировать как угодно – нельзя только ни разрывать, ни склеивать. На рис. 15 изображены три тела, шар и ещё два, каждое из которых можно преобразовать в любое другое деформацией указанного вида.

Когда говорят о запрете на склеивание, это означает, что две разные точки не должны склеиваться в одну. Пример запрещённой деформации показан на рис. 16.

Левая фигура на рис. 16 деформируется в среднюю вполне законно, а вот при переходе от средней фигуры к правой как раз и происходит склеивание. Законно деформировать правую фигуру в среднюю тоже не удаётся: в этом случае, напротив, произойдёт разрыв.

Очевидно, что деформацией без разрывов и склеиваний шар можно превратить в куб, но вот в тор превратить невозможно. С другой стороны, в тор можно превратить гирю с одной ручкой (см. рис. 12), а вот в гирю с двумя ручками превратить тор нельзя. Превращение тора в кружку с ручкой и обратно читатель может наблюдать на сайте «Википедии», на движущейся картинке в статье «Топология».

Не назвав этого понятия, мы уже познакомились с гомеоморфией. Две фигуры называются гомеоморфными, если одну можно превратить в другую путём деформации без разрывов и склеиваний; сами такие деформации называются гомеоморфизмами. Все фигуры, изображённые на рис. 15, гомеоморфны друг другу, тор гомеоморфен гире с одной ручкой и кружке с ручкой. Шар гомеоморфен кубу и пирамиде, но не гомеоморфен ни тору, ни кренделю, а последние два тела не гомеоморфны между собой. Явление гомеоморфии изучается в высшем разделе геометрии – топологии, и потому гомеоморфизмы называются также топологическими преобразованиями.

Комок (как мы его определили выше в разделе о многообразиях) – это тело, гомеоморфное шару.

Толковый словарь Ушакова определяет крендель как выпечку (сдобную витую булку) в форме буквы В. С той точки зрения, которая выражена в понятии гомеоморфии, и выпечка в форме буквы В, и выпечка в форме цифры 8, и выпечка в форме греческой буквы θ (теты, которая в русском письменном языке дореволюционной орфографии стала фитой) имеют одну и ту же форму. Даже если предположить, что хлебопёки сумели получить тесто, обладающее вышеуказанными свойствами податливости, колобок невозможно путём гомеоморфизма превратить ни в баранку, ни в крендель, как и два последних вида выпечки – друг в друга. А вот превратить шарообразный колобок в куб или в пирамиду можно. Любезный читатель сумеет найти и такой вид выпечки, в который нельзя превратить ни колобок, ни бублик, ни крендель.

Возможность превращения шара в куб и невозможность превращения его в баранку, а баранки – в крендель говорит о том, что есть некое глубинное геометрическое сходство между кубом и шаром, отсутствующее в других случаях. (Аналогично кит имеет глубинное сходство с мышью, а не с более похожей на него внешне акулой.) Указанное глубинное геометрическое сходство и формализуется в математике в виде гомеоморфии.

До сих пор мы говорили лишь о гомеоморфии трёхмерных фигур. Впрочем, нет, это неверно. Ведь наш лоскут – это, по определению, поверхность, гомеоморфная кругу. Двумерные фигуры под углом зрения гомеоморфии следует представлять себе сделанными из резиновой плёнки, которую можно как угодно мять, растягивать, сжимать; нельзя только эту плёнку ни рвать, ни склеивать; таким образом, допускаются только топологические преобразования. Вырежем из такой плёнки круг. Никаким топологическим преобразованием из него нельзя изготовить продырявленный круг, да и вообще никакой неодносвязный кусок плёнки. Зато его легко превратить в квадрат или в любой другой односвязный кусок. Но ни в поверхность шара, ни в боковую поверхность цилиндра наш круг за счёт гомеоморфизма превратить невозможно, а обе эти поверхности не превращаются ни друг в друга, ни в поверхность тора, ни в поверхность кренделя. Никакие две из рассмотренных только что поверхностей (а это были круг, круг с дыркой, сфера, боковая поверхность цилиндра, поверхность тора и поверхность кренделя) не являются гомеоморфными. Если считать, что на рис. 15 изображены не трёхмерные тела, а их поверхности, то все эти поверхности гомеоморфны друг другу.

Вспомним о спортивных гирях с любым числом ручек. Включим в этот комплект и гирю с нолём ручек (хотя на общечеловеческом языке это будет, скорее, ядро). Если гиря имеет n ручек, то её поверхность (являющаяся, как мы знаем, двумерным компактным многообразием без края) называется в топологии сферой с n ручками. Одна из замечательных теорем топологии гласит, что всякое двумерное компактное многообразие без края, являющееся частью трёхмерного пространства, гомеоморфно сфере с каким-то количеством ручек. (Слова «являющееся частью трёхмерного пространства» существенны, без них теорема неверна. Пример двумерного компактного многообразия без края, в трёхмерном пространстве не помещающегося, будет приведён в главе 12.)

Вернёмся ненадолго к проблеме Пуанкаре. И двумерная, и трёхмерная сфера односвязны, компактны и не имеют края. Вопрос в том, достаточно ли этих двух свойств для однозначного их определения. Однозначность понимается здесь в топологическом смысле, т. е. с точностью до гомеоморфии, ведь в топологии гомеоморфные геометрические фигуры не различаются, они считаются одной и той же фигурой (наподобие того, как одной и той же фигурой считаются конгруэнтные фигуры в школьной геометрии). Для двумерной сферы вопрос (который можно было бы назвать «двумерной проблемой Пуанкаре») ставится, следовательно, так: всякое ли двумерное односвязное компактное многообразие без края гомеоморфно двумерной сфере? Положительный ответ на этот вопрос был известен давно (и уж заведомо известен Пуанкаре). Если же заменить в нём слова «двумерное» и «двумерной» на «трёхмерное» и «трёхмерной», вопрос превращается в знаменитую проблему Пуанкаре, которая 100 лет не поддавалась решению; эту проблему можно назвать «трёхмерной проблемой Пуанкаре».

Можно говорить и о гомеоморфии одномерных образований – линий. С точки зрения топологии их удобно воспринимать как тонкие резиновые нити, которые допустимо изгибать, растягивать и сжимать, но нельзя рвать и склеивать. Мы вправе теперь сказать, что обрывок – это линия, гомеоморфная отрезку. Дуга окружности – обрывок, она гомеоморфна отрезку. Окружность гомеоморфна периметру квадрата и любой из линий на рис. 14, но не гомеоморфна ни линии, которая состоит из двух окружностей, пересекающихся в двух точках, ни восьмёрке, которую можно понимать как линию, состоящую из двух окружностей, соприкасающихся в одной точке; линия из окружностей, пересекающихся в двух точках, не гомеоморфна восьмёрке. Восьмёрка не гомеоморфна греческой букве θ, а буква В при одном начертании гомеоморфна букве θ, при другом – восьмёрке.

(Читатель не должен видеть противоречия в том, что выпечку в форме цифры 8, или буквы θ, или буквы В мы выше объявили гомеоморфными: ведь выпечка суть не линии, а трёхмерные тела, и указанные её виды можно непрерывно деформировать один в другой.)

Инварианты, общие для всех гомеоморфных друг другу фигур, называются топологическими инвариантами. Один такой инвариант мы уже знаем – это свойство односвязности. Предоставляем читателю осознать, что свойство односвязности действительно есть топологический инвариант, т. е. что фигура, гомеоморфная односвязной фигуре, и сама непременно односвязна. Все факты, относящиеся к геометрии положения вообще и в частности к тем задачам, которые были рассмотрены в конце главы 10, где речь шла о геометрии положения, являются топологическими инвариантами. Например, топологическим инвариантом является хроматическое число поверхности. Топология как раз и изучает топологические инварианты и в этом смысле включает в себя геометрию положения, но далеко не исчерпывается ею, поскольку среди инвариантов, изучаемых в «высокой» топологии, встречаются очень сложные и совершенно не наглядные.

Передо мной лежит небольшая (имеющая тем не менее суперобложку) книга, изданная Гостехтеориздатом в 1932 г., – Иоганн Бенедикт Листинг «Предварительные исследования по топологии». Перевод с немецкого под редакцией и с предисловием Э. Кольмана. На контртитуле указаны название и имя автора на языке оригинала: Vorstudien zur Topologie von Johann Benedict Listing, – а также место и год издания: Göttingen, 1848. Эта книга примечательна тем, что в ней в 1848 г. впервые в печати был употреблён термин «топология» в его немецком варианте – Topologie (в английском языке слово «topology» впервые появилось лишь в 1920 г.). Сам же Листинг использовал этот термин ещё раньше, в 1836 г., в письме своему школьному учителю Мюллеру, которому во многом был обязан интересом к математике и естественным наукам (и благодарен за это). Введение в научный оборот названного термина – бесспорная заслуга Листинга. (Как топологическое сочинение книжка Листинга не слишком содержательна даже по тем временам, и её одарённый автор сам это осознавал, назвав свой труд «предварительными исследованиями»; это скорее расширенный очерк, нежели книга.)

Листингу не нравились ни выражение «Analysis situs», ни «Geometria situs», и термин «топология» призван был заменить их собою. Противопоставляя метрическим соотношениям модальные, Листинг так определял значение нового термина:

Таким образом, топологии в понимании Листинга ещё очень далеко до того, что начали называть этим словом впоследствии, т. е. до общего учения о пространственных формах, рассматриваемых под углом зрения их гомеоморфии. Тем не менее его «Предварительные исследования» сыграли, как нам кажется, немаловажную роль в том, чтобы геометрия положения оформилась в область математики, постепенно развившуюся в топологию в её современном понимании. В знак признания его заслуг узел, изображённый на рис. 17, получил название узел Листинга.

Узлами Листинг заинтересовался под влиянием великого Гаусса, который едва ли не первым увидел в них математическое содержание. Гаусс обратил внимание на весьма способного и усердного студента Гёттингенского университета (Листинг поступил туда в 1830 г.). Листингу посчастливилось войти в круг ближайших учеников Гаусса, по рекомендации которого в 1839 г. он был назначен профессором физики Гёттингенского университета. Вышедшая в 1845 г. монография Листинга вошла в число классических сочинений по физиологической оптике. Биографы его утверждают, что из-за своего характера, а ещё более из-за поведения жены, он не был в чести у коллег, а потому его научные заслуги не получили должного признания. Осталось прибавить, что Листинг родился 25 июля 1808 г. и скончался 24 декабря 1882 г.

В заключение этого раздела коснёмся философского аспекта понятия гомеоморфизма. Представим себе мыслящее существо, которое живёт внутри какой-либо геометрической фигуры и лишено возможности посмотреть на эту фигуру извне, со стороны. Для него фигура, в которой оно живёт, образует вселенную. Представим себе также, что когда объемлющая фигура подвергается гомеоморфизму, то вместе с нею деформируется и всё, что находится внутри фигуры, включая все измерительные приборы и само указанное существо. Тогда для этого существа его вселенная не меняется; в частности, изометричные фигуры остаются изометричными (хотя они и перестанут быть таковыми для внешнего наблюдателя). Если, скажем, подвергнутая гомеоморфизму фигура была шаром, то существо никаким способом не может различить, пребывает ли оно по-прежнему в шаре или в том, во что этот шар превратился: например, в эллипсоиде, кубе или пирамиде. Однако для него остаётся теоретическая возможность убедиться, что его новая вселенная не имеет формы тора или кренделя.

Наше определение гомеоморфии – не определение в математическом смысле слова, а скорее, описание – нуждается в серьёзном уточнении. И вот почему. Снова взглянем на рис. 5. Будут ли гомеоморфны две изображённые на нём заузленные верёвки? Попытка преобразовать одну в другую без разрывов и склеиваний проваливается. Тем не менее в топологии эти две трёхмерные геометрические фигуры признаются гомеоморфными. Как же так?

Тут мы должны покаяться перед читателем. Дело в том, что мы его слегка обманули, изложив под видом гомеоморфии близкое, но всё же другое понятие – изотопию.

Обманули из лучших побуждений, чтобы не осложнять изложение и побыстрее ввести читателя в суть понятий. Надеемся, что, ознакомившись с дальнейшим текстом, читатель нас поймёт и простит. В качестве дополнительного оправдания приведём то обстоятельство, что в неформальном описании гомеоморфии мы всего лишь следовали устоявшейся традиции. Например, в уже упоминавшейся (в подстрочном примечании) статье «Топология» Павел Сергеевич Александров, у которого учился топологии автор этих строк, так описывает топологическое преобразование, т. е. гомеоморфизм:

Описывая гомеоморфию двух тел в терминах деформаций, мы молчаливо предполагали, что деформация происходит в трёхмерном пространстве, где и располагаются наши тела. А где же она ещё может происходить? Чтобы ответить на этот вопрос, вспомним рассуждения о конгруэнтности и изометрии из главы 10. На нескольких примерах мы показали, что изометричные фигуры, расположенные в плоскости, могут и не быть конгруэнтны относительно этой плоскости, т. е. могут не совмещаться при перемещении в её пределах. Но любые такие фигуры непременно могут быть совмещены перемещением в трёхмерном пространстве, т. е. они конгруэнтны относительно этого пространства. Теперь взглянем на рис. 4–5. Каждый из них демонстрирует фигуры, которые нельзя совместить перемещением в трёхмерном пространстве, но можно совместить перемещением в четырёхмерном пространстве (всюду – речь об евклидовых пространствах). Следовательно, не будучи конгруэнтными относительно трёхмерного пространства, они являются конгруэнтными относительно пространства четырёхмерного. (Точно так же обстояло дело с прежним Платтнером и его вернувшимся в наш мир зеркальным отражением.) Мы видим, что конгруэнтность есть понятие относительное. Бессмысленно спрашивать, конгруэнтны или нет две фигуры, не уточняя, относительно какого объемлющего пространства ставится вопрос. В отличие от конгруэнтности, изометрия есть понятие абсолютное: для утверждения, что две фигуры являются или не являются изометричными, достаточно предъявить сами эти фигуры, не спрашивая, где они расположены.

Аналогично изотопия (которую мы описали в предыдущем разделе, незаконно окрестив её гомеоморфией) – понятие относительное. Говоря об изотопии, необходимо уточнить, в каком пространстве осуществляется деформация. Заузленные верёвки на рис. 5 не деформируются друг в друга в пределах трёхмерного пространства (чтобы «перетянуть» одну в другую, её необходимо сперва разрезать, а потом склеить). Однако они деформируются («перетягиваются» без разрезов и склеиваний) в пределах пространства четырёхмерного. Иными словами, они изотопны относительно четырёхмерного пространства, но не изотопны относительно трёхмерного пространства.

Чтобы лучше усвоить понятие изотопии, зададимся вопросом: всякие ли две линии, расположенные на плоскости и преобразуемые одна в другую с выходом в трёхмерное пространство, можно преобразовать, оставаясь в пределах плоскости? Плоскость бедна многообразиями, и для них ответ положителен. А вот для произвольных линий ответ отрицательный: достаточно взять замкнутый контур «с хвостом внутрь» и замкнутый контур «с хвостом наружу» (рис. 18). Аналогична ситуация с линиями в трёхмерном пространстве; может случиться, что, будучи преобразуемыми одна в другую в четырёхмерном пространстве, две такие линии не допускают преобразования в рамках трёхмерного пространства: для примера достаточно трёхмерные вёревки с рис. 5 сжать каждую до одномерной нити. (Возникающий здесь пример с нитями показывает, что ответ для линий в трёхмерном пространстве может быть отрицателен и в том случае, если линии являются компактными многообразиями.)

Разумеется, чтобы осознать сказанное, необходимо развить воображение, ведь надлежит представлять себе деформацию геометрических фигур в четырёхмерном пространстве! Но если мы готовы согласиться с перемещениями в этом пространстве, то отчего бы не согласиться и на деформации?

А теперь изложим понятие гомеоморфии более четко. Для этого достаточно уточнить, какое преобразование одной геометрической фигуры в другую мы назовём гомеоморфизмом, поскольку гомеоморфия двух фигур есть не что иное, как возможность преобразовать одну фигуру в другую посредством гомеоморфизма. Итак, приступим.

Перечислим главные свойства гомеоморфизма. Очевидно, во-первых, что каждая точка исходной фигуры переходит в какую-то точку результирующей фигуры (а не уходит в никуда), и притом только в одну точку (а не несколько точек). Во-вторых, никакие две точки исходной фигуры не переходят в одну и ту же точку, иначе произошло бы склеивание, что запрещено. Поэтому возникающее при гомеоморфизме соответствие между точками двух фигур является взаимно однозначным: каждой точке первой фигуры соответствует ровно одна точка второй фигуры, и каждая точка второй фигуры соответствует ровно одной точке первой фигуры.

С понятием взаимно однозначного соответствия мы уже встречались в главе 7. Поскольку при взаимно однозначном соответствии точки не могут склеиваться, запрет на склеивание выполняется автоматически.

Обсудим теперь запрет на разрывы. Здесь потребуется ввести важное геометрическое понятие точки прикосновения. Вот что писал о понятии прикосновения вообще Лобачевский в своём сочинении «Новые начала геометрии с полной теорией параллельных» (упомянутом в главе 8):

Возьмём какую-нибудь геометрическую фигуру, а в ней – какую-нибудь её часть. Точка нашей фигуры называется точкой прикосновения для рассматриваемой части, если в любой близости от этой точки найдётся хотя бы одна точка указанной части. (Ясно, что каждая точка выделенной части является её точкой прикосновения, ведь в любой близости от неё найдётся она сама.) Понятие 'в любой близости' будет уточнено позже. Теперь же мы можем так сформулировать запрет на разрывы: гомеоморфизм сохраняет отношение прикосновения; это означает, что если в исходной фигуре какая-то точка была точкой прикосновения для какой-то части, то то же будет и с теми точкой и частью результирующей фигуры, в которые перейдут исходные точки и часть. (Рекомендуем читателю убедиться, что отношение прикосновения нарушается при попытке деформировать правую фигуру рис. 16 в среднюю.)

Какой смысл, вообще говоря, несет в себе утверждение, что некоторое свойство или отношение сохраняется при преобразовании? Это можно понимать в двух смыслах – слабом и сильном. Поясним на примерах. Рассмотрим преобразование натурального ряда {1, 2, 3, 4, 5, …} в множество чётных чисел {2, 4, 6, 8, 10, …}, при котором каждое число n переходит в число 2n. Рассмотрим свойство 'делиться на 4'. Ясно, что если n обладает этим свойством, то им обладает и 2n. Мы вправе сказать, что свойство 'делиться на 4' сохраняется при данном преобразовании. Однако 2n может делиться на 4 и тогда, когда n на 4 не делится (например, при n = 6). Здесь сохранение свойства понимается в слабом смысле. Сильный смысл означал бы, что 2n может делиться на 4 тогда и только тогда, когда на 4 делится n.

Именно так будет с тем же свойством 'делиться на 4' при преобразовании натурального ряда в множество {3, 6, 9, 12, 15, …}, при котором каждое число n переходит в число 3n. В дальнейшем сохранение свойств условимся понимать именно в сильном смысле. А именно: говоря про какое-то свойство, что оно сохраняется при данном преобразовании, будем иметь в виду соблюдение двух условий: во-первых, если исходный объект обладает рассматриваемым свойством, то и результирующий объект обладает этим свойством; во-вторых, если исходный объект не обладает этим свойством, то и результирующий объект им не обладает. Точно так же, в сильном смысле, будем понимать сохранение отношений. Слова «отношение сохраняется при данном преобразовании» будут означать следующее: если исходные объекты находятся в этом отношении, то и результирующие объекты находятся в том же отношении; если же исходные объекты не находятся в этом отношении, то и результирующие объекты в нём не находятся.

Суммируя сказанное, можно предложить следующее определение гомеоморфизма: гомеоморфизм есть взаимно однозначное преобразование, сохраняющее отношение прикосновения между точками и частями геометрических фигур.

По сравнению с прежним, неформальным, определением понятия гомеоморфизма в терминах деформации предложенная дефиниция не только является более строгой, но и расширяет объём этого понятия. Нетрудно убедиться, например, что интервал гомеоморфен прямой, открытый круг – плоскости, а открытый шар – всему трёхмерному пространству. Чтобы охватить подобные случаи определением через деформации, пришлось бы допускать в качестве таковых бесконечные растяжения.

Осталось выполнить данное ранее обещание и определить понятие 'в любой близости'. Каждая геометрическая фигура расположена в евклидовом пространстве какой-то размерности, а там установлено евклидово расстояние (см. главу 10). Слова «нечто найдётся в любой близости от данной точки» означают, что это «нечто» найдётся на расстоянии (от данной точки), меньшем любого наперёд заданного положительного действительного числа. Более подробно: какое положительное действительное число ни задай, интересующее нас «нечто» найдётся на таком расстоянии от рассматриваемой точки, которое меньше заданного числа. Быть может, любезному читателю покажется более простым вот какое многоступенчатое разъяснение слов «в любой близости». Сперва вводится понятие открытого шара произвольной размерности, частично знакомое нам по главе 10: открытый шар размерности n и радиуса r с центром в точке А состоит из всех точек n-мерного евклидова пространства, находящегося от А на расстоянии меньшем, нежели r. Затем для всякой точки геометрической фигуры вводится понятие окрестности этой точки: окрестностью точки называется пересечение множества всех точек фигуры с произвольным открытым шаром, центр которого находится в этой точке.

Иными словами, окрестность точки есть множество всех таких точек рассматриваемой фигуры, которые одновременно принадлежат какому-либо открытому шару. Подразумевается, что в качестве размерности всех этих открытых шаров выступает размерность того евклидова пространства, в рамках которого рассматривается наша фигура. Таким образом, каждая точка фигуры имеет бесчисленное количество окрестностей – столько же, сколько существует открытых шаров с центром в данной точке. Наконец, сообщается, что «в любой близости от данной точки» означает 'в любой окрестности данной точки'.

Если все точки прикосновения какой-либо части геометрической фигуры принадлежат самóй рассматриваемой части, эта часть называется замкнутой. Круг, например, является замкнутой частью плоскости. Его, как мы знаем, иногда называют замкнутым, чтобы отличить от открытого круга. Последний же замкнутой частью плоскости не является, поскольку среди его точек прикосновения имеются точки не принадлежащей ему окружности. Запрещению разрывов при гомеоморфизме можно теперь дать более сжатую формулировку: гомеоморфизм сохраняет свойство замкнутости. Это означает, что всякая замкнутая (незамкнутая) часть исходной фигуры обязана перейти в замкнутую же (незамкнутую) часть результирующей фигуры.

Окончательно для понятия гомеоморфизма можно предложить следующее определение: гомеоморфизм есть взаимно однозначное преобразование, сохраняющее замкнутость.

Понятие гомеоморфии позволяет предложить следующее определение n-мерного многообразия: это такая геометрическая фигура, каждая точка которой имеет окрестность, гомеоморфную n-мерному шару. Данное определение имеет тот недостаток, что наши «геометрические фигуры» расположены в евклидовых пространствах, а многие важные многообразия возникают не как подмножества евклидовых пространств, а «сами по себе». Чтобы дать определение многообразия, свободное от этого недостатка, пришлось бы вводить общее понятие абстрактного топологического пространства. Мы не будем давать точного определения этого понятия, ограничившись следующим неформальным описанием: топологическое пространство есть некое обобщение понятия геометрической фигуры, для которого имеют смысл обсуждавшиеся выше понятия прикосновения, окрестности точки, замкнутого множества и гомеоморфизма. (Указанный недостаток не слишком страшен, поскольку каждое многообразие может быть «представлено» в виде геометрической фигуры. Это значит, что для каждого многообразия существует гомеоморфная ему геометрическая фигура. Так, любое трёхмерное многообразие гомеоморфно некоторой геометрической фигуре, расположенной в пятимерном евклидовом пространстве.)

Приведем некоторые примеры многообразий, возникающих «абстрактно» в механике и геометрии.

1. Рассмотрим механическую систему, которая состоит из двух частиц, свободно передвигающихся вдоль прямой. Мы считаем, что частицы могут беспрепятственно проходить сквозь друг друга и сохраняют свою индивидуальность: они были пронумерованы, и в каждый момент нам известно, какая из частиц имеет номер один, а какая – номер два. Каково пространство состояний нашей системы? Ясно, что каждое состояние соответствует паре чисел (мы считаем, что наша прямая отождествлена с числовой прямой – для такого отождествления надо выбрать начало отсчёта, единицу длины и направление). Следовательно, пространство состояний – так называемое конфигурационное пространство – может быть отождествлено с плоскостью.

Этот простой пример можно развить в нескольких направлениях.

2. Если частиц не две, а три, мы придём к трёхмерному пространству. А если четыре – к четырёхмерному, так что мы получили простую механическую модель для четырёхмерного пространства. Правда, модель эта не даёт ответа на существенный вопрос: как же математики представляют себе это пространство? Если точка четырёхмерного пространства – это положение четырёх частиц, то что же такое, скажем, трёхмерная сфера, лежащая в этом пространстве? Формальный ответ дать несложно: это совокупность тех положений частиц, для которых фиксирована сумма квадратов расстояний от частиц до начальной точки отсчёта. Но ведь подобный ответ можно дать и в случае трёх частиц и двумерной сферы. И станет видно, как далёк такой ответ от привычного геометрического образа, связанного со словом «сфера». Так что же видят математики, думая о четырёхмерном (а то и бесконечномерном!) пространстве? Говорить об этом математики, похоже, не хотят, а возможно, и не умеют.

3. Предположим, что частиц наших по-прежнему две, но теперь они неразличимы. Положения, которые для различимых частиц мы описывали парами (x, y) и (y, x), теперь считаются одинаковыми. Будем использовать поэтому лишь такие пары (x, y), для которых x ≤ y. Тем самым мы не исключаем положений вида (x, x), когда частицы сливаются. Что теперь служит конфигурационным пространством? Ответ: многообразие, гомеоморфное полуплоскости. Действительно, те точки (x, y) плоскости, для которых x ≤ y, образуют полуплоскость.

4. Пусть теперь наши частицы скользят не по прямой, а вдоль окружности. Пусть их две и они различимы. Что будет конфигурационным пространством в этом случае? Ответ: тор (имеется в виду двумерная поверхность, а не полноторие). Действительно, при введении естественной системы координат на торе (широта и долгота) каждая точка тора соответствует паре своих «торических координат» – точек на окружности. Аналогично получаются многомерные торы (если частиц больше двух).

5. Две неразличимые частицы скользят вдоль окружности. Не будем лишать читателя удовольствия самому разобраться с тем, каким будет конфигурационное пространство в этом случае, и укажем лишь ответ: лист Мёбиуса (он будет описан в главе 12). Его краем служат те положения, при которых частицы сливаются.

6. Частиц три, они скользят вдоль окружности и неразличимы. Здесь следует уточнить, чтó понимается под положением системы. Тонкость заключается в следующем: если две из трёх частиц слились, так что мы видим только две частицы, видим ли мы при этом, где именно находится «двойная», или «тяжёлая», частица? Будем считать, что нет, не видим. Таким образом, положение или состояние системы – это (неупорядоченное) подмножество окружности, состоящее либо из трёх точек, либо из двух, либо из одной.

Для этого случая вопрос о «форме» конфигурационного пространства оказывается намного труднее, чем для предыдущих. Известный польский математик Кароль Бóрсук (Karol Borsuk, 1905–1982), внёсший значительный вклад в развитие топологии, допустил ошибку при решении этого вопроса и опубликовал неверную работу. Правильный ответ нашёл другой знаменитый тополог Рауль Ботт (Raoul Bott, 1923–2005): конфигурационное пространство в рассматриваемом случае гомеоморфно трёхмерной сфере. Положения, когда все три точки слились в одну, образуют в этой сфере нетривиальный (т. е. не перетягиваемый в окружность) узел – трилистник.

7. Ещё один пример компактного многообразия, естественным образом возникающий в механике, – пространство положений твёрдого тела с закреплённой точкой. Пусть наше тело – шар, который может как угодно вращаться в трёхмерном пространстве, однако центр его должен занимать фиксированное положение. Чтобы описать возможные положения шара, отметим на его граничной сфере точку и приложим к этой точке стрелку, указывающую определённое направление на сфере. Строго говоря, мы рассматриваем вектор, касающийся сферы в данной точке. Проследим, куда этот вектор переходит при вращении. Ясно, что, вращая шар, мы можем получить любой другой касательный вектор той же длины (примем её за единицу) и что знание этого вектора однозначно определяет положение шара. Таким образом, конфигурационное пространство в этом случае гомеоморфно пространству единичных касательных векторов к сфере. Можно доказать, что это неодносвязное компактное трёхмерное многообразие, которое может быть получено из трёхмерной сферы отождествлением всех пар антиподов (т. е. диаметрально противоположных точек). Это многообразие называется трёхмерным проективным пространством.

8. Построим теперь другой пример компактного трёхмерного многообразия, имеющий непосредственное отношение к проблеме Пуанкаре, – так называемую сферу Пуанкаре. Это пространство всех додекаэдров, вписанных в данную двумерную сферу. Его можно также получить следующим образом: сперва произвольно выберем какой-нибудь из таких вписанных додекаэдров, а затем рассмотрим все вращения сферы и отождествим те из них, при которых этот додекаэдр переходит в одно и то же положение. Каждому додекаэдру при этом соответствует 60 вращений, поскольку существует 60 вращений сферы, переводящих заданный додекаэдр сам в себя. Сфера Пуанкаре оказывается неодносвязной. Этот пример неодносвязного компактного трёхмерного многообразия принадлежит Пуанкаре. Он обнародовал его в 1904 г. в опровержение собственной неверной теоремы, опубликованной в 1900 г. Теорема утверждала, что компактное трёхмерное многообразие, в известном смысле похожее на трёхмерную сферу, и есть трёхмерная сфера (гомеоморфные многообразия считаются одним и тем же многообразием!). Обнаружив контрпример к своей теореме, Пуанкаре сформулировал её правильную (как мы теперь знаем) версию в виде знаменитой гипотезы, заметив, что её обсуждение «увело бы нас слишком далеко». Пуанкаре был прав: на доказательство его гипотезы ушло 100 лет.