Для математики значение гипотезы Пуанкаре, превратившейся теперь из гипотезы в теорему Пуанкаре – Перельмана, огромно (не зря ведь за решение проблемы был предложен миллион долларов), равно как огромно и значение найденного Перельманом способа её доказательства, но объяснить это значение здесь – вне нашего умения. Что же касается космологической стороны дела, то, возможно, значимость этого аспекта была несколько преувеличена журналистами. Впрочем, некоторые авторитетные специалисты заявляют, что осуществлённый Перельманом научный прорыв может помочь в исследовании процессов формирования чёрных дыр.

Чёрные дыры, кстати, служат прямым опровержением положения о познаваемости мира – одного из центральных положений того самого передового, единственно верного и всесильного учения, которое 70 лет насильственно вдалбливалось в наши бедные головы. Ведь, как учит физика, никакие сигналы из этих дыр не могут к нам поступать в принципе, а потому узнать, чтó там происходит, невозможно. О том, как устроена наша Вселенная в целом, мы вообще знаем очень мало, и сомнительно, что когда-нибудь узнаем больше. Да и сам смысл вопроса об её устройстве не вполне ясен. Не исключено, что этот вопрос относится к числу тех, на которые, согласно учению Будды, не существует ответа. Физика предлагает лишь модели устройства, более или менее согласующиеся с известными фактами. При этом физика, как правило, пользуется уже разработанными заготовками, предоставляемыми ей математикой.

Математика не претендует, разумеется, на то, чтобы установить какие бы то ни было геометрические свойства Вселенной. Но она позволяет осмыслить те свойства, которые открыты другими науками. Более того, она позволяет сделать более понятными некоторые такие свойства, какие трудно себе представить, она объясняет, как такое может быть. К числу подобных возможных (подчеркнём: всего лишь возможных!) свойств относятся конечность Вселенной и её неориентируемость. (Вспомним формулировку проблемы Пуанкаре и из педантизма отметим, что конечность многообразия следует из его компактности, неориентируемость же, напротив, несовместима с односвязностью.)

Долгое время единственной мыслимой моделью геометрического строения Вселенной служило трёхмерное евклидово пространство, т. е. такое, которое известно всем и каждому со средней школы. Это пространство бесконечно; казалось, что никакие другие представления и невозможны; помыслить о конечности Вселенной казалось безумием (не меньшим, чем несколько тысяч лет назад мысль об обращении Земли вокруг Солнца). Однако ныне представление о конечности Вселенной не менее законно, чем представление о её бесконечности. В частности, конечна трёхмерная сфера. От общения с физиками у меня осталось впечатление, что одни отвечают: «Скорее всего, Вселенная бесконечна», другие же: «Скорее всего, Вселенная конечна», и только единицы не имеют определённой точки зрения.

Ниже мы попытаемся объяснить теоретическую возможность конечности Вселенной. Пока что заметим лишь, что конечность Вселенной не означает существования у неё края, «стены». Ведь само по себе отсутствие у геометрической фигуры конца и края ещё не означает её бесконечности. Поверхность нашей планеты, например, конечна, но края у неё нет. Но это мы твёрдо знаем всего несколько сот лет. В детстве я, как и другие, наслаждался старинной картинкой, на которой был изображён монах, дошедший до Края Земли и просунувший голову сквозь небесный свод. Ещё более, чем упомянутая картинка, моё детское воображение увлекала модная гипотеза (потом она как-то заглохла), что некие две далёкие туманности, наблюдаемые с Земли в противоположных концах небосвода, являются на самом деле не различными астрономическими объектами, а одним и тем же объектом, видимым с разных сторон. Подтвердись такое, это было бы доказательством конечности Вселенной.

Вот три мысленных эксперимента, способных засвидетельствовать конечность Вселенной, если она действительно имеет место. Первый: экспериментатор отправляется в космическое путешествие и, двигаясь всё время в одну сторону, возвращается в исходную точку. Второй: длина окружности оказывается меньше той, которую сообщают нам в школе, т. е. меньше 2π, помноженных на длину радиуса, причём отличие от «школьной» длины тем больше, чем длиннее радиус. Третий (предложен Эйнштейном): экспериментатор окружает себя сферой из прочной и неограниченно растягивающейся плёнки и начинает эту сферу раздувать; площадь поверхности сферы сперва будет возрастать, но начиная с некоторого момента начнет уменьшаться, а в итоге вся сфера стянется в точку. Этот третий эксперимент можно изложить и несколько иначе – в терминах намазывания краски на шар для игры в кегли, крокет или бильярд; можно взять и мяч. Предполагается, что краска имеется в неограниченном количестве. Экспериментатор покрывает шар всё новыми и новыми слоями краски, так что радиус шара неуклонно возрастает, поверхность же его уплощается, становясь всё менее и менее выпуклой. В какой-то момент экспериментатор замечает, что поверхность перестаёт быть выпуклой, она начинает прогибаться в другую сторону (так и хочется сказать «становится впуклой»). А ещё через некоторое время экспериментатор обнаруживает себя не вне той сферы, каковой является поверхность окрашиваемого шара, а внутри неё, т. е. внутри сферической полости. Он продолжает накладывать краску на «стены» полости до тех пор, пока эти сжимающиеся «стены» его не стискивают совершенно.

Чтобы понять, как такое возможно, надо напрячь воображение, а затем рассуждать по аналогии. С этой целью мы слегка изменим наше представление о Флатландии. В главе 10 Флатландия была плоской, теперь будет сферической. Желающие могут представить себе очень тонкий слой между двумя концентрическими двумерными сферами – столь тонкий, что его толщиной мы пренебрегаем, считая, что её нет вовсе. Таким образом, новая Флатландия двумерна, как и прежде; она населена двумерными существами, флатландцами. Мы с вами живём на сфере (на поверхности Земли), флатландцы же пребывают в теле сферы, в её «толще»; эта «толща», конечно, не имеет толщины, но ведь и флатландцы её не имеют. Органы чувств не позволяют флатландцам ощутить что-нибудь вне пределов этой сферы, которая для них составляет вселенную. Двумерная сфера, образующая Флатландию, большая, а двумерные жители обитают на малом её участке и – внимание! – полагают, что их вселенная представляет собою двумерное евклидово пространство, т. е. плоскость. (Полезно вспомнить, что люди тысячелетиями были убеждены: поверхность Земли – плоская. И, надо сказать, имели к тому разумные основания.)

Посмотрим, что может поколебать флатландцев в убеждении, что их вселенная, Флатландия, плоская. Если считать, что флатландцы умеют видеть чрезвычайно далеко, то удалённый от них объект они видят с двух сторон, ведь в их вселенной луч света идёт по сфере, огибая её. Флатландец, совершающий космическое путешествие и двигающийся всё время в одну сторону, возвращается, обогнув сферу, в исходную точку. Радиус окружности двумерные существа проводят по сфере, и потому длина «флатландского радиуса» оказывается больше евклидова радиуса той же окружности, проведённого в недоступном флатландцам «внешнем» пространстве. Следовательно, длина окружности окажется меньшей, нежели та, которая получится, если по известной школьной формуле умножить «флатландский радиус» на 2π. Если окружность невелика, то указанную разницу невозможно уловить измерительными приборами, имеющимися во флатландских исследовательских центрах; если же окружность достаточно велика, эта разность становится очень заметной. Посмотрим теперь, чтó произойдёт, если двумерный экспериментатор окружит себя канцелярской резинкой, способной неограниченно растягиваться, придаст ей форму окружности и станет увеличивать радиус этой окружности. Сперва длина окружности будет возрастать, но после прохождения через «экватор» Флатландии она начнёт уменьшаться и в итоге уменьшится до ноля. В качестве шаров для игр у флатландцев выступают круги. Если начать красить такой круг (что во Флатландии означает наносить краску на окружность круга, причём наносить её снаружи), то сперва круг будет расширяться, оставаясь для красильщика выпуклым, но только пока радиус круга не сравняется с «флатландским радиусом» всей Флатландии. После этого момента красильщик будет ощущать себя внутри сужающегося круга.

А теперь картину, только что изложенную нами для двумерного мира, надо по аналогии перенести на мир трёхмерный. Мы, как и флатландцы, убеждены, что пребываем в «прямом» евклидовом пространстве школьной геометрии. Однако не исключено, что на самом деле – в (не на, а в) сфере, только трёхмерной. И эту трёхмерную сферу можно представлять себе расположенной в евклидовом четырёхмерном пространстве – наподобие того, как двумерная сфера расположена в пространстве трёхмерном. Четырёхмерное пространство мы, разумеется, не воспринимаем своими органами чувств, но ведь и флатландцы не воспринимают пространства трёхмерного. Как и флатландцы, мы можем убедиться в кривизне мира, увидев какой-нибудь весьма отдалённый предмет с двух противоположных сторон или отправившись в космическое путешествие и, никуда не сворачивая, вернувшись на космодром отправления. Можно также сравнивать длины окружностей с теми, которые выражаются через их радиусы по стандартной, известной из школы формуле. Вместо эксперимента с канцелярской резинкой надлежит произвести тот эксперимент с растягивающейся плёнкой, о котором было сказано выше.

Нередко представления об устройстве Вселенной, уже включённые наукой в перечень подтверждённых, кажутся парадоксальными; не исключено, что некоторые её свойства могут оказаться ещё более невероятными. Пожалуй, сейчас уже всем известен так называемый парадокс близнецов. Если один из двух близнецов совершает космическое путешествие, а другой остаётся на Земле, то в момент возвращения из космоса космонавт непременно окажется моложе своего брата; если ускорения, которым подвергался космонавт во время путешествия, были достаточно велики или достаточно длительны, разница в возрасте будет заметна на глаз. Разумеется, если они будут слишком велики, космонавт погибнет, а если слишком длительны – вряд ли он (а тем более его оставшийся на Земле близнец) окажется в живых к моменту возвращения, так что, говоря о «заметной на глаз разнице», мы допустили художественное преувеличение. Но незаметная глазу разница действительно имеет место.

Сейчас мы опишем другое явление – парадокс зеркального отражения. Встретится ли он когда-либо в действительности, неизвестно. В отличие от парадокса близнецов, описывающего реальные (точнее сказать, общепризнанные) свойства мироздания, парадокс зеркального отражения – чисто теоретическое построение, возможность его воплощения в реальности всего лишь не опровергнута.

Итак, парадокс зеркального отражения. Вспомним случай с Готфридом Платтнером, придуманный Уэллсом и дважды пересказанный нами. Платтнер на время исчезает, а по возвращении оказывается зеркально перевёрнутым. Уэллс не видит иного способа объяснить происшествие, кроме как приписать его выходу в другой мир, в четвёртое измерение: «Единственный способ, посредством которого правая и левая сторона какого-нибудь твёрдого тела могут перемениться, – это если изъять тело из пространства (в том виде, в каком мы понимаем пространство)».

Здесь существенна заключённая в скобки оговорка «в том виде, в каком мы понимаем пространство». Имеется в виду стандартное, школьное понимание пространства. Математики, однако, обнаружили теоретическую возможность существования такой формы трёхмерного пространства, что поменять местами правую и левую части тела можно и без выхода за его пределы. При стандартном, школьном понимании формы окружающего нас трёхмерного пространства действительно никаким перемещением в этом пространстве невозможно превратить кисть правой руки в кисть левой руки. Но это невозможно именно при стандартном, школьном понимании. Существуют, однако, иные формы пространства, допускающие такое перемещение. Попытаемся разъяснить, как такое может быть.

Как справедливо замечает Уэллс, вырезанный из бумаги силуэт правой ладони невозможно превратить в силуэт левой ладони, ограничиваясь перемещением по плоской поверхности стола; чтобы это сделать, надо поднять силуэт над столом, т. е. выйти в третье измерение, перевернуть силуэт и снова положить на стол.

Существуют, однако, такие поверхности, при перемещении по которым правое может превратиться в левое, а левое – в правое. Самой простой и самой известной из таких поверхностей является лист Мёбиуса (Möbius strip) или – как эту поверхность называли в добрые старые времена – лента Мёбиуса (Möbius band). Лента Мёбиуса показана на рис. 19. Знаменитый голландский художник Эшер (Мaurits Cornelis Escher, 1898–1972) увековечил ленту Мёбиуса в своём параде муравьёв, ползущих по ней друг за другом (рис. 20). Изображение ленты Мёбиуса можно встретить на обложках математических изданий и значках математических сообществ (в частности, на значке мехмата МГУ).

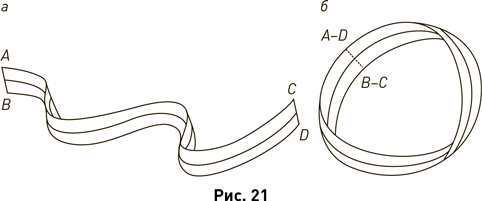
При желании читатель может сам изготовить ленту Мёбиуса. Сделать это просто. Если взять бумажную или матерчатую ленту и склеить её торцы, то полученная поверхность будет боковой поверхностью цилиндра. Если же при этом ленту перекрутить, т. е., удерживая неподвижным один конец ленты, другой конец повернуть перед склеиванием на 180°, как раз и получится лента Мёбиуса. Сказанное иллюстрирует рис. 21. Если взять ленту с двумя длинными сторонами AC и BD и двумя короткими, торцевыми, сторонами AB и CD (рис. 21, а) и склеить торцы AB и CD без перекручивания, точка A склеится с точкой C, а точка B – с точкой D, и получится боковая поверхность цилиндра. Если же A склеить с D, а B – с C, получим ленту Мёбиуса (рис. 21, б). Случается, что, подпоясавшись и застегнув ремень, вы обнаруживаете, что ремень перекрутился; такой перекрученный и застёгнутый ремень может служить примером ленты Мёбиуса. Боковая поверхность цилиндра имеет два края, лента же Мёбиуса – только один (подобно тому, как один край имеет круг).

Самое же замечательное, что лента Мёбиуса имеет всего лишь одну сторону. Муравей, ползущий по одной стороне вырезанного из плоскости круга, не может перейти на другую его сторону, не переползя через край. Тот же муравей, ползающий по внешней стороне сферы, не может попасть внутрь сферы, не прогрызя её насквозь; а если он ползёт по внутренней стороне сферы, то точно так же должен её прогрызть, чтобы вырваться наружу. И поверхность в виде круга, и поверхность в виде сферы имеют каждая по две стороны. Иное дело лента Мёбиуса. Пусть теперь наш муравей ползает по ней. Проделаем такой мысленный эксперимент. Сделаем клон муравья и пустим его ползти, оставив исходного, клонированного, муравья на месте. Мы обнаружим, что, следуя определённым маршрутом, клон достигнет того же места ленты, что и клонированный муравей, но только оба насекомых окажутся в положении антиподов по отношению друг к другу: каждый относительно другого будет обращен спиной вниз. Лист бумаги можно закрасить с одной стороны в чёрный цвет, оставив другую его сторону незакрашенной. Точно так же и боковую поверхность цилиндра, и сферу можно выкрасить с одной стороны, оставив другую незакрашенной. Поступить так с лентой Мёбиуса не удастся. И плоскость, и её кусок, и поверхность цилиндра, и сфера суть поверхности двусторонние. Лента же Мёбиуса является односторонней поверхностью.

Феномен ленты Мёбиуса был обнаружен в 1858 г. Первооткрывателем его стал уже известный нам по предыдущей главе Листинг; ему же принадлежит и первое сообщение в печати. Однако описание свойств этой поверхности первым дал другой немецкий математик – Август Фердинанд Мёбиус (August Ferdinand Möbius, 1790–1868). Среди его предков со стороны матери был Лютер, а среди учителей – Гаусс. Память Мёбиуса увековечена не только в названии знаменитой поверхности, но также в названии кратера на обратной стороне Луны и астероида 28516. Дело в том, что, хотя основные его научные труды – труды замечательные, высоко оценённые Гауссом – относились к области математики, по должности он был астроном – профессор астрономии Лейпцигского университета (и в качестве такового внёс заметный вклад в эту науку двумя монографиями по теоретической астрономии). Преподавал же он в основном механику. Начинал Мёбиус младшим сотрудником астрономической обсерватории, причём утверждают, что он согласился на такую скромную работу из-за низкой самооценки. Его скромность, впрочем, была вознаграждена, потому что директором астрономической обсерватории в Гёттингене оказался не кто иной, как Гаусс.

В предыдущей главе была приведена предложенная Мёбиусом в 1840 г. задача, аттестующая его как одного из пионеров геометрии положения. За десять лет до кончины Мёбиус представил рукопись об односторонних поверхностях (в частности, о той, которая была впоследствии названа его именем) в Парижскую академию наук (как неофициально именовалась Французская академия естественных наук). Академия эта, увы, была печально известна тем, что присланные рукописи подчас пылились на полках и никто их не читал. А иногда они и пропадали. Слава богу, рукопись Мёбиуса не пропала и после его смерти была обнаружена.

Другое свойство ленты Мёбиуса особенно важно для нашего изложения. Оно состоит в так называемой неориентируемости. Лента Мёбиуса, как и всякая поверхность, не имеет толщины. Если на какой-то поверхности изображён силуэт ладони, то невозможно сказать, правая она или левая: это зависит от того, с какой стороны посмотреть. Сказанное верно и для ленты Мёбиуса. (Читатель да не смутится употреблением здесь слова «сторона». Лента Мёбиуса в целом является односторонней, но тот малый её участок, на котором изображена ладонь, – двусторонний, и как ни гуляй по нему, своим антиподом не станешь.) Если рядом изображены две ладони, то можно сказать, одинаковы ли они, или же одна есть зеркальное отражение другой. Так вот, можно так переместить силуэт ладони по ленте Мёбиуса, что он вернётся на прежнее место зеркально отражённым, а возможность подобного передвижения и означает неориентируемость. Каждый может удостовериться, что это вполне реально. Для наглядности полезно представлять себе ленту Мёбиуса изготовленной из промокательной бумаги, так что любой рисунок, нанесённый чернилами, проступает насквозь. Не менее полезно воображать, что лента Мёбиуса сделана из бумаги, которая благодаря своей ничтожной толщине совершенно прозрачна, так что рисунок, нанесённый на одну сторону, ясно виден и с другой.

Если же перемещать изображение ладони по плоскости или по сфере, то, как его ни двигай, оно никогда не превратится в своё зеркальное отражение: и плоскость, и сфера суть поверхности ориентируемые.

Ориентируемость и неориентируемость геометрических образований – настолько важные понятия, что мы сейчас приведём ещё одну наглядную их иллюстрацию. Поставим спичку вертикально головкой вверх на горизонтальную плоскость и будем по ней передвигать; ясно, что спичка будет всё время торчать головкой вверх. Возьмём вместо плоскости сферу; если первоначально спичка была направлена головкой наружу, то так оно и останется при любых передвижениях; то же с заменой слова «наружу» на слово «внутрь». Это тот же мысленный эксперимент, который ранее мы изложили в муравьиных терминах. Теперь обведем основание спички окружностью, расположенной в нашей плоскости – не на плоскости, а в её «нолевой толще». Зададим на окружности так называемую ориентацию: нарисуем на ней дугообразную стрелку, указывающую направление обхода окружности. Этот обход, если смотреть на окружность с головки спички, может совершаться в одном из двух направлений – по ходу или против хода стрелки часов; каждое из этих двух направлений и называется ориентацией окружности. Ясно, что при описанном выше движении спички по плоскости ориентация привязанной к спичке окружности (которая будет передвигаться в плоскости) останется одной и той же. Это и есть ориентируемость плоскости. То же самое можно проделать, заменив плоскость сферой: ориентация передвигающейся окружности вместе со спичкой окружности меняться не будет. Это и есть ориентируемость сферы. Если же передвигать спичку, не отрывая её основания от ленты Мёбиуса, то можно добиться того, чтобы она пришла в положение, при котором ориентация окружности, описанной в ленте у основания спички, сменится на противоположную. Этот мысленный эксперимент демонстрирует неориентируемость ленты Мёбиуса.

Лента Мёбиуса имеет край, и её можно сшить из конечного числа лоскутов. Поэтому она является компактным двумерным многообразием с краем. Отодрать от неё край в реальном, физическом смысле, конечно, нельзя. Да ведь и сама лента Мёбиуса не является, строго говоря, реальным, физическим объектом: она есть не имеющая толщины поверхность и, как и всякая идеальная поверхность, пребывает лишь в нашем воображении (поразительным образом одинаковом в подобных случаях у разных людей). Но мысленно удалить край можно. Оставшееся будет двумерным многообразием без края, но уже не компактным: из конечного числа лоскутов это многообразие сшить нельзя, но можно сшить из бесконечного числа лоскутов, уменьшающихся в размерах по мере приближения к отсутствующему краю.

А возможна ли такая поверхность, которая, как и лента Мёбиуса, неориентируема, но является компактным многообразием без края? Такие поверхности существуют, но только в нашем обычном трёхмерном пространстве они не умещаются. Одной из них является знаменитая бутылка Клейна, названная по имени немецкого математика Феликса Клейна, запустившего её в математический оборот в 1874 г.

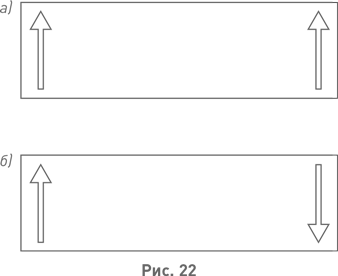
Постараемся в меру наших сил объяснить, как она получается. С этой целью вернёмся к той процедуре получения из обычной ленты цилиндрической поверхности и ленты Мёбиуса, которая была показана на рис. 21, а и б. Исходную ленту будем изображать в виде прямоугольника. Не станем помечать буквами его углы, а вместо этого воспользуемся стрелками. Они будут указывать способ склеивания. Требуется, чтобы при склейке направления, указанные стрелками, совпали. Схема получения боковой поверхности цилиндра показана на рис. 22, а. Видно, что у получающейся поверхности два края, один из коих соответствует острым концам стрелок, а другой – тупым. Что же касается ленты Мёбиуса, то схема её получения изображена на рис. 22, б. Наглядно видно, что у ленты Мёбиуса только один край, поскольку правый верхний угол теперь склеивается с левым нижним углом.

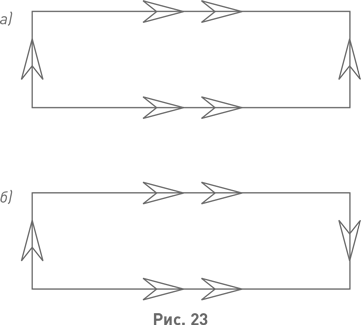
До сих пор мы склеивали только боковые стороны исходной ленты. А что, если попытаться склеить между собой также и другие две стороны? При склейке, показанной на рис. 23, а, получится тор. Если же склеить, как показано на рис. 23, б, как раз и получится бутылка Клейна. Легко увидеть, что и тор, и бутылку Клейна можно сшить из конечного числа лоскутов. А значит, обе поверхности суть двумерные компактные многообразия. Поскольку все стороны многоугольника участвуют в склеивании, краю в результирующих поверхностях неоткуда взяться. Поэтому и тор, и бутылка Клейна являются многообразиями без края.

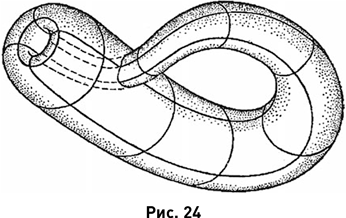
Но всё дело в том, что склеить стороны так, как предписывает рис. 23, б, оставаясь в пределах нашего привычного трёхмерного пространства, невозможно. Это возможно лишь в том случае, если мы научимся действовать в пространстве четырёхмерном (кто знает, может быть, когда-нибудь и научимся). В четырёхмерном пространстве бутылка Клейна (в проекции на трёхмерное пространство) выглядит так, как показано на рис. 24.

Точнее сказать, так выглядит одна из гомеоморфных друг другу (и даже изотопных в четырёхмерном пространстве) фигур, каждую из которых можно назвать бутылкой Клейна (ведь и листу Мёбиуса можно придать различные формы, но все они будут гомеоморфны друг другу). Лучше сказать, что на рис. 24 предъявлена некоторая «бутылочная репрезентация» бутылки Клейна.

Не исключено, что более наглядным окажется другое объяснение того, как построить бутылку Клейна. Начнём с ленты Мёбиуса. Приглашаем читателя взглянуть на рис. 25, а и б. На них изображены два недостроенных плоских кольца; назовём их недокольцами. Чтобы достроить каждое недокольцо до полного кольца, нужно закрыть имеющуюся щель. Представим себе эти недокольца сделанными из абсолютно растяжимой резиновой плёнки. Тогда можно, не выходя из плоскости, стянуть эти недокольца так, чтобы в каждом из них края щели сомкнулись. Торцевые отрезки, образующие края щели, при этом склеиваются. Теперь потребуем дополнительно, чтобы при стягивании слились и одинаковые цифры, стоящие по концам склеиваемых торцевых отрезков. Для фигуры на рис. 25, а это возможно, а для фигуры на рис. 25, б – нет; напомним, что мы говорим о стягивании в пределах плоскости. Однако и для фигуры на рис. 25, б есть способ склеить торцевые отрезки так, чтобы совпали одинаковые цифры. Только для этого надо осуществить операцию не на плоскости, а в трёхмерном пространстве. При этом получится не плоское кольцо, а лента Мёбиуса.

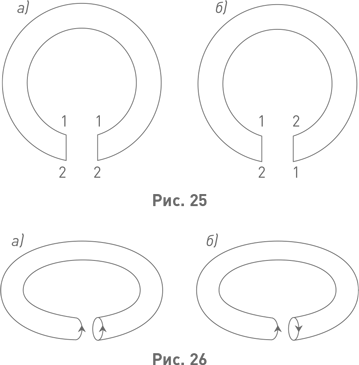
Теперь взглянем на рис. 26, а и б. На них изображены баранки, в каждой из которых выгрызена щель. Говоря научным языком, на них изображены торы со щелями. Края щелей представляют собою круги. На окружностях этих кругов поставлены стрелки, указывающие направления обхода. Исходим из того, что фигуры с рис. 26, а и б сделаны из неограниченно растягиваемой резины, так что в каждой из фигур края щели можно затянуть. Упомянутые окружности при этом склеятся, а фигура превратится в тор. Усложним задачу, потребовав, чтобы при склеивании окружностей совпали направления их обхода. Мы видим, что это осуществимо для фигуры с рис. 26, а и неосуществимо для фигуры с рис. 26, б. Здесь имеется в виду осуществимость посредством деформации в пределах трёхмерного пространства. Однако и для фигуры с рис. 26, б есть способ стянуть края щели так, чтобы направления обхода склеиваемых окружностей совпали. Только для этого надо осуществить операцию не в трёхмерном пространстве, а в четырёхмерном. При этом получится не тор, а бутылка Клейна. Любезный читатель не преминет заметить аналогию между только что изложенным сопоставительным построением тора и бутылки Клейна и построением, также сопоставительным, плоского кольца и ленты Мёбиуса, изложенным в предыдущем абзаце.

Столь длительное обсуждение неориентируемых поверхностей, т. е. фигур двумерных, играло в нашем изложении роль разбега перед прыжком, длительность которого по сравнению с разбегом мала. Аналогом же прыжка у нас будет следующий за сим абзац, посвящённый неориентируемым трёхмерным фигурам.

Трёхмерную геометрическую фигуру, которая была бы неориентируемой, т. е. такую, внутри которой может существовать траектория, приводящая к зеркальному отражению, – подобную фигуру представить себе очень трудно. Тем не менее таковые допускают математическое построение. В нашем обычном трёхмерном пространстве они не умещаются. Те из них, которые компактны и не имеют края, не умещаются даже в «обычном» (евклидовом) четырёхмерном пространстве, подобно тому как неориентируемые компактные поверхности без края не умещаются в трёхмерном пространстве (вспомним, что умещающаяся в трёхмерном пространстве лента Мёбиуса имеет край). Однако уже не вызывает протеста предположение о существовании таких фигур в высших измерениях, ведь и двумерная лента Мёбиуса, не умещаясь на плоскости, требует для своего размещения трёхмерного пространства. И действительно, все неориентируемые трёхмерные тела «хорошо себя чувствуют» в пятимерном евклидовом пространстве.

Вспомним путешествие Готфрида Платтнера, в результате которого он превратился в своё зеркальное отражение. И евклидово пространство из курса средней школы, и трёхмерная сфера ориентируемы. В них отсутствуют траектории, приводящие к зеркальному отражению. Но теоретические представления о возможной геометрической структуре Вселенной не исключают того, что она неориентируема. А тогда путешествие, приводящее к зеркальному отражению путешественника, может быть осуществлено и без выхода из нашего трёхмерного мира. Возможно, таким образом, не вполне прав был поэт, сказавший: