Книга: Апология математики (сборник статей)
Назад: Глава 9 Проблема на миллион долларов
Дальше: Глава 11 От геометрии положения к топологии
Глава 10
От метрической геометрии к геометрии положения
Геометрические фигуры
Следуя принципу Колмогорова, мы начнём с цитаты из классического школьного учебника Киселёва – «кристальной киселёвской "Геометрии"», по словам Солженицына. Боюсь, что читатель XXI в. может и не знать, кто такой Киселёв. Андрей Петрович Киселёв (1852–1940) – великий просветитель в области математики, по его учебникам арифметики, алгебры и геометрии учились многие поколения российских школьников (в частности, те, которым было суждено составить впоследствии славу российской математики). Киселёвым были последовательно подготовлены к изданию «Систематический курс арифметики для средних учебных заведений» (1884), «Элементарная алгебра» (1888), «Элементарная геометрия» (1892). Эти учебники выдержали десятки изданий до революции и десятки изданий после (в советское время они назывались короче: «Арифметика», «Алгебра», «Геометрия»). Следует сказать, что в советское время они подвергались редактированию, подчас значительному, что не всегда делало их лучше. Поэтому цитату мы приведём из § 6 дореволюционного, 1917 г., 26-го издания «Элементарной геометрии» (разбиение на абзацы сохраняем лишь частично):
Всякая ограниченная часть пространства называется геометрическим телом. Геометрическое тело можно подразделить на части; каждая часть геометрического тела есть также геометрическое тело. Граница геометрического тела, т. е. то, чем оно отделяется от остального пространства, называется поверхностью. Поверхность можно подразделять на части; всякая часть поверхности есть также поверхность. Граница поверхности или части поверхности называется линией. Линию можно также подразделять на части; каждая часть линии есть также линия. Граница линии или части линии называется точкой. Геометрическое тело, поверхность, линия и точка не существуют раздельно. Однако при помощи отвлечения мы можем рассматривать поверхность независимо от геометрического тела, линию – независимо от поверхности и точку – независимо от линии. При этом поверхность мы должны представлять себе не имеющею толщины, линию – не имеющею ни толщины, ни ширины и точку – не имеющею ни длины, ни толщины.Всякая линия содержит в себе бесчисленное множество точек. Принято говорить, что эти точки лежат на линии или что эта линия проходит через эти точки. Их можно рассматривать как последовательные положения одной и той же точки, движущейся вдоль этой линии. Поэтому можно сказать, что линия есть след движения точки. Если, например, мы остриё карандаша двигаем по бумаге, то след этого движения на бумаге есть приблизительно линия; приблизительно потому, что остриё карандаша не представляет собою геометрической точки, вследствие чего проведённая на бумаге линия имеет некоторую ширину (и даже толщину). Чем острее очинён карандаш, тем более остриё его приближается к геометрической точке и тем более линия, проведённая этим остриём, приближается к геометрической линии. Подобно этому поверхность можно рассматривать как след движения линии, движущейся в пространстве некоторым образом.Совокупность каких бы то ни было точек, линий, поверхностей или тел, расположенных известным образом в пространстве, называется вообще геометрической фигурой.
Образуют ли геометрическую фигуру два не имеющих общих точек шара? Если исходить из точного смысла последней фразы приведённой цитаты, ответ должен быть утвердительным. Но нам хотелось бы получить право говорить, что это не фигура, а две фигуры. Поэтому мы включим в понятие фигуры дополнительное требование связности. Связность фигуры означает, что любые две её точки можно соединить линией, не выходящей за пределы фигуры. В дальнейшем, говоря «фигура», мы всегда будем подразумевать её связность.
Геометрические фигуры бывают плоские и пространственные («объёмные»); последние называются геометрическими телами. Примерами тел, изучаемых в средней школе, служат пирамиды, параллелепипеды, шары, конусы, цилиндры. Плоскую фигуру можно определить как часть плоскости, пространственную – как часть пространства. Плоские фигуры изучаются в планиметрии, пространственные – в стереометрии. Текст из учебника Киселёва написан с позиции стереометрии, в ней все геометрические фигуры, включая поверхности и линии, видятся расположенными в пространстве. При изучении планиметрии слово «поверхность» не произносят, хотя все такие плоские фигуры, как круг или многоугольник, при включении их в дискурс (автор не смог удержаться от искушения употребить модное словцо) стереометрии являются поверхностями.
Термин, обозначающий математическое понятие 'поверхность', как в русском, так и в других языках, происходит от бытового представления о поверхности чего-нибудь – стола, воды, Земли. Это прослеживается и в приведённой цитате. Однако такое понимание создает определённые неудобства. Скажем, чтобы подвести под определение поверхности платок (толщиной платка мы пренебрегаем), который может быть и не плоским, его необходимо непременно представить себе границей какого-то тела или дополнить до такой границы. Полезно поэтому иметь в виду следующее. Источником понятия (не слова, а понятия!) поверхности служит представление об очень тонком слое. Аналогично источником понятия линии служит представление об очень тонкой нити. Можно сказать, что поверхность – это бесконечно тонкий слой, линия – бесконечно тонкая нить (а точка – бесконечно малый кружочек). Вопрос к читателю: сфера – это тело или поверхность? Если отождествлять, как это нередко делают, понятия 'сфера' и 'шар', тогда, конечно, сфера есть тело. Но такое отождествление терминологически неправильно. Терминологически правильный ответ таков: сфера – это поверхность шара, а шар – это часть пространства, ограниченная сферой. Точно так же окружность – это граница круга, а круг – это часть плоскости, ограниченная окружностью.
А теперь посмотрим на тор. Тор – эта геометрическое тело, к форме которого в той или иной степени приближаются баранка, бублик, спасательный круг, обруч хулахуп. Энциклопедические словари определяют тор как геометрическое тело, полученное вращением круга вокруг оси, расположенной вне этого круга. Но прибавляют: «Поверхность, ограничивающую тор, иногда также называют тором». Если тор понимают как тело, то его поверхность называют поверхностью тора. Если же тор понимают как поверхность, то ограниченное ею тело называют полноторием – с двумя употребительными вариантами именительного падежа: полноторие и полноторий. Но чаще всего, пренебрегая тонкостями, говорят просто «тор», извлекая смысл из контекста. Автор не уверен, что сумеет избежать подобной двусмысленности, устраняемой лишь контекстом, но будет очень стараться. И тор как тело и тор как поверхность не односвязны (это слово пока для нас всего лишь термин из формулировки проблемы Пуанкаре, а что оно значит, будет объяснено ниже).
Равенство, конгруэнтность, конгруэнция, изометрия
В средней школе, как известно, вводится понятие равенства геометрических фигур, в частности треугольников. В § 35 уже цитированного учебника Киселёва говорится: «Два многоугольника, как вообще две какие-нибудь геометрические фигуры, считаются равными, если они при наложении могут быть совмещены».
Хотелось бы привлечь внимание любезного читателя к тому, что Киселёв употребляет слово «считаются», подчёркивая тем самым конвенциональность (условность) термина «равный», определение которому даётся в цитате. Потому что основное значение этого термина состоит в совпадении. Когда говорят, что дважды два равно четырём, то имеют в виду, что число с именем «дважды два» и число с именем «четыре» – это одно и то же число. Именно такое совпадение и выражает знак равенства в формуле 2 · 2 = 4 (совпадение не выражений 2 · 2 и 4, а тех сущностей, которые обозначены этими выражениями). То же происходит и в обычном языке. Как мы уже отмечали, когда говорят «все люди равны», то непременно прибавляют (или подразумевают), в чём они равны: в правах, достоинстве или в чём-то ином. Но выяснить, совпадение каких сущностей имеется в виду при определении равенства многоугольников или в чём равны эти многоугольники, не так-то просто. Андрей Петрович Кисёлев в приведённой цитате вынужден констатировать принятое в школьной математике словоупотребление. Видимо, он сам от него не в восторге, что доказывается нижеследующим подстрочным примечанием к слову «совмещены», где то, что в предыдущей цитате было названо равенством, получает более правильное название конгруэнтность:
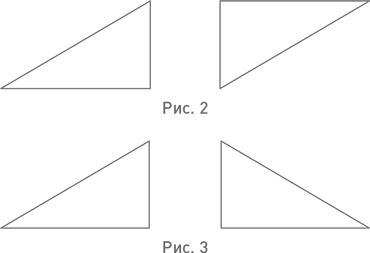
Фигуры, могущие совместиться при наложении, называются конгруэнтными, а самое совмещение – конгруэнцией. Различают конгруэнцию прямую и непрямую. Прямою конгруэнция называется тогда, когда совмещение может быть выполнено посредством передвижения одной из конгруэнтных фигур по плоскости, в которой фигуры лежат; если же для совмещения фигур такого передвижения недостаточно, но надо ещё перевернуть одну из фигур другою стороною, то конгруэнция называется непрямою. Например, треугольники, изображённые на рис. 2, прямо конгруэнтны, а треугольники на рис. 3 непрямо конгруэнтны.
К сожалению, сделав это примечание, Киселёв уступает сложившейся практике и в дальнейшем термин «конгруэнтный» не употребляет. Что же касается фигур стереометрии, то даже и термин «равенство» применяется в учебнике Киселёва только к трёхгранным углам, да и то лишь в параграфах, набранных мелким шрифтом (§ 401–402).
Мы же будем следовать сделанному Киселёвым примечанию и применительно к геометрическим фигурам вместо школярского слова «равно» употреблять слово «конгруэнтно». Вот ещё пример на противопоставление прямой и непрямой конгруэнций: начертания прописных букв Р и Ь не являются прямо конгруэнтными, но непрямо конгруэнтны. Ясно, что в случае пространственных фигур непрямая конгруэнция невозможна, поскольку невозможно «перевернуть одну из фигур другою стороною». Поэтому человек не конгруэнтен своему отражению в зеркале, а правая кисть руки не конгруэнтна левой. Простой геометрический пример зеркально симметричных, но не конгруэнтных тел дан на рис. 4. Более изысканный пример представлен на рис. 5, где изображены два заузленных верёвочных кольца (при математическом изучении узлов их свободные концы принято склеивать, чтобы узел было невозможно развязать).
Откажемся от понятия непрямой конгруэнции (тем более что её нет для фигур стереометрии) и будем отныне конгруэнтными называть только такие фигуры, которые допускают прямую конгруэнцию, т. е. совпадающие при перемещении. И здесь мы подходим к представлению почти философскому – представлению об относительности конгруэнтности. Треугольники, показанные на рис. 3, оказываются неконгруэнтными, если числить их по ведомству плоскости, т. е. рассматривать, не выходя за пределы той плоскости, в которой они расположены; и они же конгруэнтны, если числить их расположенными в пространстве и тем самым разрешать выход за пределы плоскости. То же самое можно отнести к силуэтам или отпечаткам левой и правой ладоней: они конгруэнтны относительно пространства, но не конгруэнтны относительно плоскости.
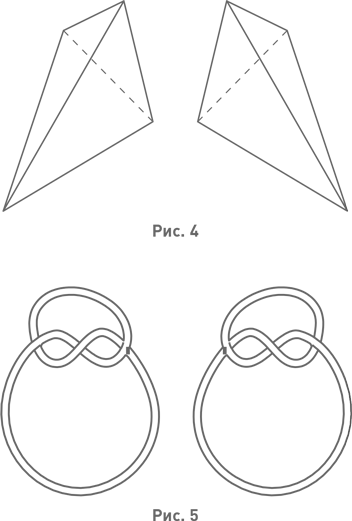
Тем не менее очевидно наличие некой общности между членами каждой из пар фигур, представленных на рис. 2–5. Та же общность связывает левую и правую кисти рук, а также любой предмет с его отражением в зеркале. Сказать, что эта общность заключается в равенстве размеров, недостаточно. Каких именно размеров? Ведь, скажем, существуют весьма отличающиеся на глаз ромбы с совпадающими длинами сторон: бывают – или надо сказать «были»? – подставки для чайников в виде ромба с шарнирами по углам, изменяющие свою форму. Речь идёт о равенстве всех размеров, но это, конечно, требует уточнения. С этой целью вспомним обсуждавшееся в главе 7 понятие взаимно однозначного соответствия и рассмотрим взаимно однозначное соответствие между множеством всех точек одной геометрической фигуры и множеством всех точек другой фигуры. Это соответствие называется изометрическим, коль скоро сохраняются расстояния между точками. Слова «сохраняются расстояния между точками» расшифровываются следующим образом: пусть при рассматриваемом соответствии точкам А и В первой фигуры соответствуют точки А1 и В1 второй фигуры; тогда расстояние между А1 и В1 должно быть равно расстоянию между А и В. Две геометрические фигуры называются изометричными, коль скоро между множествами их точек можно установить изометрическое соответствие. Каждый из треугольников на рис. 2 изометричен другому. То же справедливо для треугольников на рис. 3, для треугольных пирамид на рис. 4, для узлов на рис. 5. Левая и правая кисти изометричны; произвольный предмет изометричен своему зеркальному отражению. Понятие изометричности (она же изометрия), в отличие от конгруэнтности, абсолютно: наличие или отсутствие у фигур изометрии не зависит от того, рассматриваются ли они планиметрически, в пределах плоскости, или же стереометрически, в пределах пространства.
ВАЖНОЕ ЗАМЕЧАНИЕ. Если две фигуры, расположенные в одной и той же плоскости, изометричны друг другу, то они конгруэнтны, т. е. могут быть совмещены путём перемещения (возможно, с выходом в пространство, за пределы плоскости). Изометричные фигуры в пространстве необязательно конгруэнтны, т. е. необязательно допускают совмещение посредством перемещения (см. рис. 4–5).
Четвёртое измерение – брать пример с мыслителей Флатландии
Первоначальный вариант очерка «Апология математики» был напечатан в журнале «Новый мир» в 2007 г., в последних двух номерах. Статью прочёл Андрей Анатольевич Зализняк и 7 января 2008 г. прислал мне письмо, в котором, в частности, отмечал:
В некоторых случаях мне очень не хватает каких-то Ваших «человеческих» (образных, через аналогии и т. п.) попыток помочь читателю выйти мыслью за рамки своего нормального земного мышления. Так, мне кажется, всё это у Вас сделано, например, в вопросе о параллельных. Но мне очень хотелось бы чего-то подобного, в частности, в вопросе о четвёртом и прочих измерениях. Мне кажется, Вы не учитываете, что для 99 % читателей (из тех, кто вообще слыхал, что бывает больше чем три измерения) четыре измерения – это три обычных измерения + время (так сказать, хронотоп). И что они, следовательно, думают совсем не о том, читая Вас.Нет ли способа дать читателю хоть какой-нибудь glimpse о том, в каком примерно направлении (по сравнению с земной жизнью) устремляют своё воображение математики, когда они создают понятие четвёртого (пятого и т. д.) измерения? Ведь не из землемерия же это родилось. На Ваших страницах понятие четвёртого измерения появляется, если не ошибаюсь, так, как если бы читателю оно уже должно было быть если не понятным, то по крайней мере привычным.Признаюсь, что без этого лично я не смог составить себе ни какого удовлетворительного представления о том, что такое трёхмерная сфера и, следовательно, о теореме Пуанкаре – Перельмана.
В настоящей подглавке я старался, как мог, исполнить пожелания Андрея Анатольевича.
Линии (в частности, прямые и окружности) одномерны, поверхности (в частности, плоскости и сферы) двумерны, точки нольмерны. Смысл этого утверждения можно пояснить следующим образом. Положение точки, лежащей на линии, задаётся указанием одного действительного числа; положение точки, лежащей на поверхности, – указанием двух чисел; чтобы задать положение точки в пределах самой этой точки, не нужно вообще никаких чисел, поскольку возможен лишь единственный вариант. Числа, задающие положение точки, называются её координатами. Таким образом, положение точки на линии определяется одной координатой, на поверхности – двумя координатами, на точке (или в точке – не знаю, как лучше) – нолём (нулём) координат. Координатой точки на линии может служить расстояние, пройденное этой точкой при движении вдоль линии (мы ссылаемся здесь на цитату из Киселёва). Посмотрим, откуда могут взяться (возможны и другие способы!) те две координаты, которые определяют положение точки на поверхности. Первая координата – это координата рассматриваемой точки на той линии, движением которой образована наша поверхность. Вторая координата – это то расстояние, которое прошла точка при движении линии по поверхности; данное расстояние может измеряться длиной, углом или ещё как-нибудь. Когда в школе в рамках курса математики изучают координаты на плоскости (абсциссу и ординату), исходят из измерения длин. Когда же на уроках географии знакомятся с координатами на поверхности Земли (широтой и долготой), исходят из измерения углов. Рекомендуем читателю подумать, как можно ввести координаты на поверхности тора.
Тела трёхмерны, и положение точки тела определяется тремя координатами. Чтобы задать, скажем, положение точки в толще Земли, надо указать две координаты на поверхности и затем третью, показывающую глубину.
В нашем мире нет четырёхмерных геометрических фигур. Но если очень напрячь воображение, можно представить себе их существование. Для этого перенесёмся в воображаемый плоский мир, так называемую Флатландию. Флатландия – это плоскость, населённая плоскими, не имеющими толщины существами – флатландцами.
Для них двумерная плоскость – это их мир, их вселенная; третье измерение недоступно их опыту. Они живут не на, а в плоскости (мы бы сказали «в её толще», если бы плоскость имела толщину). Представить себе трёхмерные тела они не в состоянии, но понимают, что такое два, одно и ноль измерений. Слово «поверхность» во флатландском языке отсутствует, поскольку нет ничего, что могло бы иметь поверхность. На уроках математики флатландским школьникам объясняют, что нет и не может быть такой прямой, которая проходила бы через вершину прямого угла и была перпендикулярна к двум его сторонам. Но некоторые флатландцы путём напряженных размышлений чисто умозрительно додумались до возможности существования трёхмерного мира с расположенными в нём трёхмерными телами, мира понятного нам с вами, живущим в этом мире, уважаемый читатель, флатландцам же недоступного. Эти же флатландцы утверждают, что если такой мир существует, то существует и та прямая, невозможность существования которой доказывают в школах; эта прямая протыкает Флатландию насквозь в вершине упомянутого прямого угла. Для пишущего эти строки важно, чтобы читатель понял, как устроена Флатландия, и проникся мировоззрением флатландцев. Может быть, кому-то покажется более понятным такая псевдофизическая модель Флатландии. Вместо плоскости возьмём тонкий слой, ограниченный двумя параллельными плоскостями (для наглядности – горизонтальными). Потребуем, чтобы в этом слое действовало следующее мироустройство: все геометрические фигуры состоят не из точек, как мы привыкли, а из вертикальных отрезков, перпендикулярных к ограничивающим плоскостям и упирающихся в них концами. Отрезки эти неделимы, как атомы в представлениях, державшихся до начала ХХ в.; никаких частей у вертикальных отрезков не существует. Все движения в слое происходят лишь вдоль ограничивающих плоскостей; направлений вверх и вниз просто-напросто не существует. Это и будет Флатландия, мир которой, с точки зрения его обитателей, двумерен.
Вот так и мы, следуя примеру философов и математиков Флатландии, усилием воображения можем допустить существование четырёхмерного мира с расположенными в нём четырёхмерными геометрическими фигурами – гипертелами. Мы не назвали их четырёхмерными телами, чтобы избежать путаницы. Ведь в принятой нами системе терминов слово «тело» уже подразумевает трёхмерность.
Путаница может возникнуть и со словом «пространство». Оно очень многозначно. К сожалению, все его значения важны, поэтому выбрать какое-либо одно из них, а остальные запретить невозможно. В цитате из учебника Киселёва этим словом обозначалось обычное, «школьное» пространство, в котором располагаются шары и многогранники.
Это пространство трёхмерно и евклидово (термин будет разъяснён далее). В школе молчаливо предполагают, что это и есть то физическое пространство, которое нас окружает, говоря попросту, «наше пространство». (В главе 8 мы вкратце обсудили возможность того, что физическое пространство не является евклидовым.)
Вернёмся на несколько минут к Флатландии. Треугольники, изображенные на рис. 3, не конгруэнтны относительно плоскости, но – для нас! – конгруэнтны относительно пространства. С флатландской же точки зрения, они, разумеется, изометричны, но не конгруэнтны ни в каком смысле, поскольку возможности выхода в трёхмерное пространство не существует во флатландском миропонимании. Но это если говорить о миропонимании флатландского обывателя, «человека с улицы». Однако, как уже было сказано, некоторые флатландские мыслители осознали теоретическую возможность существования третьего измерения и того, что указанные треугольники конгруэнтны относительно трёхмерного мира. Таким образом, эти мыслители (математики, философы, фантасты) допускают возможность такого, выходящего за пределы Флатландии перемещения, при котором один из треугольников с рис. 3 превратится в другой. Попытаемся взять пример с этих продвинутых, пытливых флатландцев и допустить, скажем, такое выводящее за пределы нашей трёхмерной Вселенной перемещение, при котором одна из пирамид с рис. 4 превращается в другую. Собственно, нет нужды ходить за примерами в Флатландию, вдохновляющий пример можно найти и на Земле, а именно у Г. Дж. Уэллса.
В 1896 г. Уэллс написал уже упоминавшуюся «Историю Платтнера» – рассказ о том, как школьный учитель Готфрид Платтнер, совершивший фантастическое путешествие, возвращается из него зеркально перевёрнутым. До путешествия он не был левшой, и тело его имело нормальное строение, за исключением лёгкой асимметрии: «Левый глаз немного больше правого, и челюсть чуть-чуть отвисает с левой стороны». А вот каким он сделался после путешествия: «Правый глаз немного больше левого, и правая часть челюсти слегка тяжелее левой. ‹…› Сердце Готфрида бьётся с правой стороны! ‹…› Все другие несимметричные части его тела расположены не на своих местах. Правая доля его печени расположена с левой стороны, левая – с правой, аналогично перепутаны и лёгкие. ‹…› Он может писать только левой рукой, причём справа налево». Заметим, что «новый» Платтнер изометричен самому себе «старому».
Уэллс объясняет происшедшие с Платтнером изменения выходом в другой мир, в четвёртое измерение: «Если вы вырежете из бумаги любую фигуру, имеющую правую и левую стороны, вы можете легко переместить эти стороны, если поднимете и перевернёте фигуру. Но с предметом объёмным дело обстоит иначе. Теоретики-математики говорят нам, что единственный способ, посредством которого правая и левая сторона какого-нибудь твёрдого тела могут перемениться, – это если изъять тело из пространства (в том виде, в каком мы понимаем пространство), вынуть его из обычных условий и переместить куда-то вне пространства. ‹…› Случившаяся у Платтнера перемена местами правой и левой частей есть не что иное, как доказательство того, что он переходил из нашего пространства в так называемое Четвёртое Измерение, а затем снова вернулся в Наш Мир».
Называя пространство евклидовым, мы тем самым подчёркиваем, что в нём выполняются аксиомы Евклида. В школьной математике слова «трёхмерное» и «евклидово» опускают и говорят просто «пространство», предполагая его и евклидовым, и трёхмерным. В этом пространстве, в отличие от Флатландии, можно найти три попарно перпендикулярных луча, исходящих из одной точки, но вот четвёртого луча, перпендикулярного к этим трём, найти не удаётся; более того, можно доказать, что такого луча и не существует. Однако если допустить возможность прямых, протыкающих пространство ровно в одной точке, то можно построить и четвёртый луч.
Евклидово расстояние
Евклидовость пространства можно определить и без ссылок на аксиомы Евклида. Дело в том, что в трёхмерном евклидовом пространстве расстояние s между точкой с координатами (x1, y1, z1) и точкой с координатами (x2, y2, z2) задаётся формулой
s² = (x1 – x2)² + (y1 – y2)² + (z1 – z2)².
Вот эта формула задания расстояний в трёхмерном пространстве и определяет его евклидовость. Иначе говоря, евклидовым называют такое трёхмерное пространство, в котором расстояние задаётся указанной формулой.
На плоскости расстояние s между двумя точками с координатами (x1, y1) и (x2, y2) задаётся формулой
s² = (x1 – x2)² + (y1 – y2)².
Поэтому плоскость называют двумерным евклидовым пространством.
На прямой расстояние s между двумя точками с координатами x1 и x2 задаётся формулой
s² = (x1 – x2)².
Поэтому прямую называют одномерным евклидовым пространством.
Расстояния, определяемые выписанными формулами, называются евклидовыми. Приведём для ясности пример неевклидовых расстояний. Таковы, в частности, все расстояния, измеряемые по поверхности Земли, если считать Землю эллипсоидом. Чтобы получить евклидово расстояние между двумя точками на земной поверхности, надо провести через эти две точки прямую, которая неизбежно будет проходить в толще планеты, и измерить длину соединяющего точки отрезка. Для жителей Земли, однако, больший интерес представляют именно расстояния по поверхности.
Надеемся, читатель уже понял, что положение точки в четырёхмерном пространстве задаётся четырьмя координатами. При этом евклидовость четырёхмерного пространства означает, что евклидовым является расстояние s между точкой с координатами (x1, y1, z1, u1) и точкой с координатами (x2, y2, z2, u2), т. е. что оно задаётся формулой
s² = (x1 – x2)² + (y1 – y2)² + (z1 – z2)² + (u1 – u2)².
Точка в шестимерном пространстве имеет шесть координат. Предоставляем читателю написать формулу евклидова расстояния между точкой с координатами (x1, y1, z1, u1, v1, w1) и точкой с координатами (x2, y2, z2, u2, v2, w2).
В математике принято отождествлять точку с набором её координат. При таком отождествлении точка прямой – это просто-напросто действительное число, а прямая (она же одномерное евклидово пространство) – это множество всех действительных чисел с евклидовым расстоянием между ними. Точно так же точка плоскости (двумерного евклидова пространства) – это пара действительных чисел (x, y), а сама плоскость – множество всех пар действительных чисел с евклидовым расстоянием между парами. Трёхмерное, четырёхмерное и т. д. пространство – это множество всех троек (всех четвёрок и т. д.) действительных чисел (x, y, z) с евклидовым расстоянием между тройками (четвёрками и т. д.).
Таким образом, нет нужды воображать существование какого-то четырёхмерного мира, объемлющего наш трёхмерный. Можно ограничиться изучением четвёрок действительных чисел и евклидовых расстояний между этими четвёрками. В своих строгих рассуждениях математики так и поступают. Однако одновременно пользуются и геометрическими образами, как если бы четырёхмерный мир существовал.
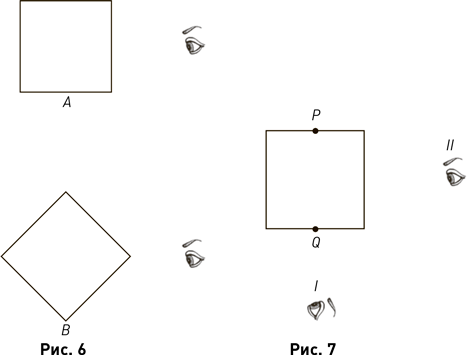
Более того, некоторые математики (автор этих строк к ним не принадлежит) выработали в себе значительную геометрическую интуицию и способны «видеть» (внутренним зрением, разумеется) фигуры четырёхмерного пространства. В мои студенческие годы желающих, среди которых был и я, собрали в одной из больших аудиторий университета и показали фильм «Вращение куба в четырёхмерном пространстве». На экране мелькали отрезки, я мало что понял, но впечатлился. Сделаю робкую попытку пояснить читателю, что именно происходило. Представим себе квадрат, расположенный в Флатландии, вращение этого квадрата вокруг его центра в пределах флатландской плоскости и флатландца, наблюдающего это вращение. На рис. 6 показаны два положения квадрата – А и B и наблюдающий флатландец (точнее, его глаз). Когда квадрат находится в положении А, наблюдатель видит отрезок, длина которого равна стороне квадрата. Когда квадрат придёт в положение B, наблюдатель увидит отрезок, длина которого равна диагонали квадрата. Во время вращения наблюдатель будет видеть отрезок варьирующейся длины, которая непрерывно изменяется от длины стороны до длины диагонали и обратно. Теперь представим себе другую картину. Примем, что квадрат состоит из одних своих сторон, а внутри он пустой. Пусть он вращается вокруг оси, проходящей через середины P и Q противоположных сторон, – с выходом за пределы Флатландии. На рис. 7 показаны два флатландских наблюдателя I и II. Что они увидят? Для наблюдателя I точки P и Q сольются в одну, её он будет видеть всё время, а в какой-то миг – проходящий через неё отрезок. Наблюдатель II будет всё время видеть две точки P и Q, а в какой-то миг – сторону квадрата, которая заслонит собою эти точки. Этот миг наступит, когда все стороны квадрата окажутся во Флатландии. А теперь представим себе, что вращение вокруг оси PQ некто, находящийся в трёхмерном, внешнем по отношению к Флатландии, пространстве, снимает (на плёнку, на диск или на что ещё теперь снимают), а затем показывает на плоском экране. Что увидит зритель на экране? Он увидит мелькание сторон периодически меняющего свою форму четырёхугольника. Аналогично если оператор, пребывающий в четырёхмерном, внешнем по отношении к нашему трёхмерному миру, пространстве, заснимет вращение куба, то мы увидим на экране мелькание граней этого куба. Что и узрели в конце 1940-х гг. студенты мехмата МГУ.
Таким образом, мы видим два подхода к многомерной (в частности, четырёхмерной) евклидовой геометрии, различающиеся скорее психологически, чем сущностно. При одном подходе четырёхмерное, пятимерное и т. д. евклидово пространство (как и пространства трёхмерное, двумерное, одномерное) состоит из геометрических точек, и каждая точка имеет числовые координаты. При другом оно состоит из наборов чисел, каковые наборы и являются точками. Каждый из этих подходов предполагает, что расстояние между точками евклидово. Наибольшую пользу приносит сочетание двух этих подходов. (Здесь прослеживается некоторая отдалённая аналогия с физикой, где электрон – и частица, и волна одновременно.)
Георгию Борисовичу Шабату принадлежит замечательный термин «плюриагорафобия» – боязнь многомерного пространства. В порядке борьбы с этой фобией слегка прикоснёмся к представлению о четырёхмерном кубе.
Возьмём единичный квадрат (квадрат со стороной, длина которой равна единице), такой, что одна из его вершин расположена в начале координат, а две другие – по координатным осям. Координаты его вершин таковы: (0, 0); (0, 1); (1, 0); (1, 1). Его граница состоит из четырёх отрезков.
Теперь возьмём единичный куб, одна вершина которого помещается в начале координат, а три другие – по координатным осям. Координаты восьми его вершин таковы: (0, 0, 0); (0, 0, 1); (0, 1, 0); (0, 1, 1); (1, 0, 0); (1, 0, 1); (1, 1, 0); (1, 1, 1). Его граница состоит из шести квадратов.
Иногда бывает удобным называть квадраты двумерными кубами, а отрезки – одномерными кубами.
Четырёхмерный куб имеет 16 вершин. Если поместить одну из них в начале координат, а четыре других – по четырём координатным осям, то, предполагая по-прежнему, что длина стороны равна единице, получим такие координаты вершин: (0, 0, 0, 0); (0, 0, 0, 1); (0, 0, 1, 0); (0, 0, 1, 1); (0, 1, 0, 0); (0, 1, 0, 1); (0, 1, 1, 0); (0, 1, 1, 1); (1, 0, 0, 0); (1, 0, 0, 1); (1, 0, 1, 0); (1, 0, 1, 1); (1, 1, 0, 0); (1, 1, 0, 1); (1, 1, 1, 0); (1, 1, 1, 1). Его граница состоит из восьми трёхмерных кубов.
Сказанное имело, в частности, целью сообщить мыслям читателя некоторую инерцию, с тем чтобы подвести его к понятию трёхмерной сферы, используемому в формулировке проблемы Пуанкаре. (Как видим, инерция мышления – это не всегда плохо.) Продолжим набирать инерцию.
Обычная сфера – это поверхность шара, двумерная, как всякая поверхность. Мы так и будем говорить – двумерная сфера. Из каких точек она состоит? Из всех точек трёхмерного евклидова пространства, находящихся на одном и том же расстоянии от некоторой выделенной точки, называемой центром и сфере не принадлежащей; указанное расстояние называется радиусом сферы. Обозначим координаты центра сферы буквами a, b, c. А если отождествлять точку с набором её координат, то можно сказать, что центр нашей сферы – это точка (a, b, c). Пользуясь формулой евклидова расстояния в трёхмерном пространстве, мы вправе сказать, что двумерная сфера с радиусом r состоит из всех таких точек (x, y, z) трёхмерного пространства, которые удовлетворяют уравнению
(x – a)² + (y – b)² + (z – c)² = r².
Трёхмерный шар, ограниченный этой двумерной сферой (он же просто шар в общеупотребительном значении этого слова), состоит из всех таких точек (x, y, z) трёхмерного пространства, которые удовлетворяют неравенству
(x – a)² + (y – b)² + (z – c)² ≤ r².
Если заменить здесь знак ≤ неравенства на знак < строгого неравенства, получим так называемый открытый шар, граница которого (двумерная сфера) удалена. Он состоит из всех таких точек (x, y, z), для которых
(x – a)² + (y – b)² + (z – c)² < r².
Если желают подчеркнуть разницу между шаром, содержащим ограничивающую его сферу, и открытым шаром, первый называют замкнутым.
Давайте теперь поразмыслим, что такое одномерная сфера. Определение строим по аналогии с определением двумерной сферы: одномерная сфера состоит из всех точек двумерного евклидова пространства, находящихся на одном и том же расстоянии, называемом радиусом, от некоторой выделенной точки, называемой центром. Поскольку двумерное евклидово пространство – это не что иное, как плоскость, то ясно, что одномерная сфера – это просто-напросто окружность. Если обозначить радиус буквой r, а координаты центра – буквами a и b, то становится ясным, что одномерная сфера есть множество всех таких точек (x, y) двумерного пространства, которые удовлетворяют уравнению
(x – a)² + (y – b)² = r².
Это и есть знакомое (как мы надеемся) по средней школе уравнение окружности. Окружность ограничивает круг, точки которого удовлетворяют нестрогому неравенству
(x – a)² + (y – b)² ≤ r².
Круг можно назвать двумерным шаром. А как следует назвать множество всех точек плоскости, удовлетворяющих строгому неравенству
(x – a)² + (y – b)² < r²?
Позволю себе высказать убеждение, что читатель уже догадался: это множество называется открытым кругом (или открытым двумерным шаром), а определяемый нестрогим неравенством просто круг называют, чтобы противопоставить его открытому кругу, замкнутым кругом.
Каждая трёхмерная сфера ограничивает четырёхмерный шар. И те и другие недоступны нашему непосредственному наблюдению, и представить их себе в качестве геометрических объектов нам так же трудно, как Василию Ивановичу из анекдота – квадратный трёхчлен. Но всё сказанное до сих пор приходит нам на помощь. Читатель уже сам, без подсказки, мог бы заключить, что трёхмерная сфера состоит из всех точек четырёхмерного евклидова пространства, находящихся на одном и том же расстоянии, называемом радиусом, от некоторой выделенной точки, называемой центром и сфере не принадлежащей. Обозначая радиус буквой r, а координаты центра – буквами a, b, c, d, получаем, что трёхмерная сфера радиуса r состоит из всех таких точек (x, y, z, u) четырёхмерного пространства, которые удовлетворяют уравнению
(x – a)² + (y – b)² + (z – c)² + (u – d)² = r².
А тот четырёхмерный шар (он же замкнутый четырёхмерный шар), границей которого эта трёхмерная сфера служит, состоит из всех таких точек (x, y, z, u) четырёхмерного пространства, которые удовлетворяют неравенству
(x – a)² + (y – b)² + (z – c)² + (u – d)² ≤ r².
Призываем читателя выписать соотношение для точек открытого четырёхмерного шара.
Если же мы желаем тем или иным образом представить себе трёхмерную сферу как «геометрический объект» (а не просто множество числовых четвёрок), как гипертело, то у нас вместе с Василием Ивановичем нет другого выхода, как взять пример с мыслителей Флатландии, которые находятся на передовом крае флатландской науки. Увидеть двумерную сферу непосредственно они не могут – только одномерную, т. е. окружность. Но они пришли к мысли, что в трёхмерном пространстве существуют двумерные сферы. А самые смелые из них допустили даже, что сама Флатландия не плоскость, а двумерная сфера очень большого радиуса (настолько большого, что на ограниченном обитаемом участке Флатландии кривизна незаметна); большинство из этих смельчаков были сожжены на кострах за вольнодумство. Вот так и мы, если уж допускаем четырёхмерное пространство как некую недоступную нам реальность, то допускаем и существование «геометрической» трёхмерной сферы. Не исключено, что все мы как раз и пребываем в трёхмерной сфере, каковой является наша Вселенная. В осознании такой возможности некоторую роль играет результат Перельмана.
Геометрия положения
Все понятия и факты, о которых говорилось до сих пор в этой главе, принадлежали так называемой метрической геометрии, которая основана на понятии расстояния и изучает метрические инварианты, т. е. свойства, общие для всех изометричных друг другу фигур. Именно эту геометрию изучают в средней школе. А разве бывает другая? Бывает, и к этой другой (возможно, точнее было бы сказать «к одной из таких других») мы собираемся перейти. Вот два примера геометрических задач, никак не связанных с понятием расстояния:
задача Мёбиуса – в 1840 г. Август Фердинанд Мёбиус, о котором будет рассказано в главе 12, предложил такую задачу: «Жил-был король, и было у него пять сыновей. В своём завещании он указал, что после его смерти королевство должно быть разделено между его сыновьями на пять областей, причём каждая область должна иметь общую границу с каждой из остальных четырёх. Может ли быть исполнено это завещание?»;задача о пяти городах – можно ли пять городов соединить, каждый с каждым, непересекающимися дорогами?
Для обеих задач ответ отрицательный. Произвольно выберите пять точек на какой-либо поверхности и попытайтесь соединить их каждую с каждой непересекающимися линиями, проходящими по той же поверхности. Вы легко сделаете это на поверхности тора. А вот ни на плоскости, ни на сфере сделать это вам не удастся.
Не удастся также исполнить королевское завещание в любом королевстве, расположенном на плоскости или на сфере. На торе же может сыскаться королевство, в котором последняя воля короля будет исполнена. Заметим, что из отсутствия решения для задачи о пяти городах вытекает отсутствие решения и для задачи Мёбиуса. В самом деле, если бы разделение королевства на пять областей, удовлетворяющее требуемому свойству, было возможным, то, соединив столицы соседних областей дорогой, пересекающей общую границу, мы получили бы пять городов, соединённых непересекающимися дорогами.
Чтобы не перегружать изложение, мы не формулировали явно, а лишь подразумевали нижеследующее требование. Предполагается, что каждая область гомеоморфна кругу.
Подробнее о понятии гомеоморфии мы поговорим в главе 11. Пока же нам будет достаточно следующего понимания фразы «область гомеоморфна кругу». Нанесём нашу область на плёнку, сделанную из неограниченно растяжимого и неограниченно сжимаемого материала, и вырежем её из плёнки по контуру границы. Гомеоморфность кругу означает, что без разрывов и склеиваний нашу область можно деформировать в круг. Например, кругу гомеоморфен не только квадрат и вообще любой многоугольник, но и боковая поверхность конуса, а также боковая поверхность цилиндра, если прорезать в ней щель.
А вот вам ещё один пример – эйлерова характеристика поверхности. Вообразим себе планету, поверхность которой состоит из материка и окружающего его океана. На материке расположены страны, каждая из которых как геометрическая фигура гомеоморфна кругу. (Для ясности: Италия не такова, в состав её входят острова, и уже потому она не гомеоморфна кругу. Впрочем, не такова и её материковая часть, поскольку Ватикан и Сан-Марино создают в ней «дыры».) Океан, царство Нептуна, также объявляется страной. Нарисуем на глобусе политическую карту планеты. Узлом назовём всякую точку, где сходятся несколько границ, ребром – участок границы между соседними узлами. К общему числу стран прибавим общее число узлов и затем вычтем общее число рёбер. Мы обязательно получим число два. Данный факт и составляет содержание знаменитой теоремы Эйлера, в справедливости которой приглашаем читателя убедиться на примерах. Число два называется эйлеровой характеристикой сферы.
Оказывается, эйлерова характеристика существует у многих поверхностей (в частности, у любой компактной поверхности, а что это такое, будет разъяснено в главе 11). Наличие у данной поверхности эйлеровой характеристики означает следующий замечательный факт: какую карту ни начерти на рассматриваемой поверхности, вычитание числа границ из суммы числа стран и числа узлов всегда даёт один и тот же результат. Любознательный читатель может сам подобным же образом вычислить эйлерову характеристику поверхности тора и убедиться, что она равна нолю. Для этого достаточно нарисовать какую-нибудь карту на торе, не забывая при этом, что каждая страна должна быть гомеоморфна кругу, а затем из суммы числа стран и числа узлов вычесть число рёбер.
Все приведённые наглядные примеры принадлежат геометрии положения. Довольно давно было замечено, что некоторые геометрические задачи, подобные задаче о пяти городах и дорогах между ними, имеют качественный (а не количественный!) характер. Вот другая задача того же типа: провести непересекающиеся дороги от каждого из трёх домов к каждому из трёх колодцев; ни на плоскости, ни на сфере это невозможно, но возможно на поверхности тора. Для исследования таких задач совершенно несущественны размеры фигур и даже пропорции этих размеров – существенно лишь взаимное расположение точек и линий. Математическую дисциплину, которая этим занимается, ещё до её возникновения Лейбниц предложил называть Analysis situs (анализ положения) или Geometria situs (геометрия положения). Пуанкаре писал в трактате «Наука и метод» в главе «Будущее математики»:
Есть дисциплина, которую называют Analysis situs и предметом изучения которой являются соотношения расположений различных элементов фигуры независимо от их величины. Эта геометрия – чисто качественная: её теоремы остались бы справедливыми, если бы точные фигуры были заменены грубыми изображениями, созданными ребёнком. Можно построить также Analysis situs более чем трёх измерений. Важность Analysis situs огромна, и я не думаю, чтобы его значение могло быть преувеличено…
Смеем надеяться, что слова о более чем трёх измерениях не остались не замеченными читателем.
Есть две известные задачи геометрии положения, взятые из реальной жизни, причём вторая имела и практическое значение.
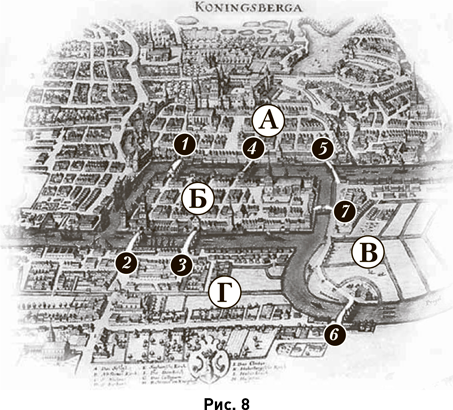
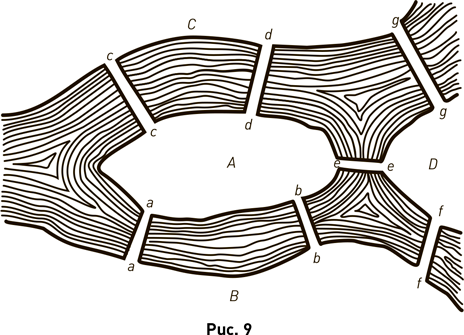
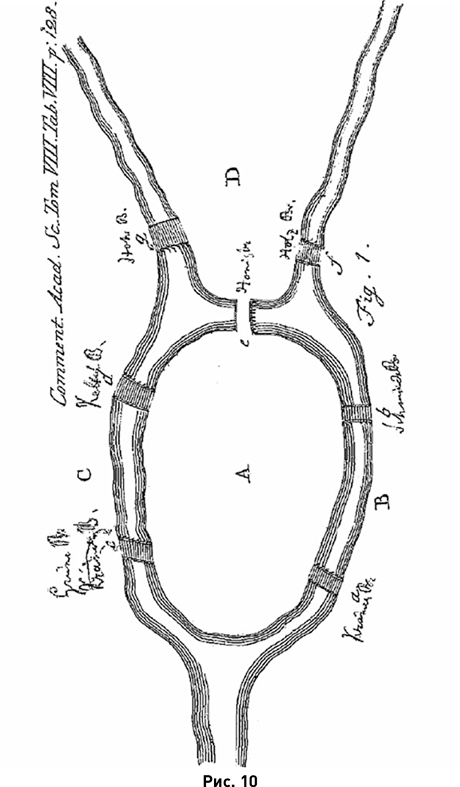
Первая – это знаменитая задача о кёнигсбергских мостах. Река Прегóля (Прегель), протекающая через город Кёнигсберг (переименованный 4 июля 1946 г. в честь скончавшегося 3 июня того же года, но никак не связанного с городом М. И. Калинина в Калининград), образует различные протоки, через которые были перекинуты семь мостов. На рис. 8 представлена старинная карта города. Буквы и цифры, добавленные к ней, обозначают части города (А – Альтштадт, Б – Кнайпхоф, В – Ломзе, Г – Форштадт) и мосты [в порядке строительства: 1 – Лавочный (Торговый), 2 – Зелёный, 3 – Рабочий (Мусорный), 4 – Кузнечный, 5 – Деревянный, 6 – Высокий, 7 – Медовый]. Рис. 10 воспроизводит план расположения мостов, начертанный самим Эйлером. Если на этом плане прочесть их немецкие названия, то можно увидеть, что карта на рис. 8 и план на рис. 10 повёрнуты относительно друг друга. В схематическом виде план Эйлера повторён на рис. 9. Немецкие названия мостов написаны на плане не слишком разборчиво, поэтому мы приведём их здесь, слегка осовременив орфографию (Эйлер для всех названий употреблял раздельные написания): a – a – Krämerbrücke (Лавочный, или Торговый, мост), b – b – Schmiedebrücke (Кузнечный мост), c – c – Grüne brücke (Зелёный мост), d – d – Köttelbrücke (Рабочий, или Мусорный, мост), e – e – Honigbrücke (Медовый мост), f – f – Holzbrücke (Деревянный мост), g – g – Hohe brücke (Высокий мост).
На Эйлеровом плане видна надпись: Comment. Acad. Sc. Она расшифровывается как Commentarii Academiae Scientiarum Imperialis Petropolitanae, что в переводе с латинского означает «Записки Императорской Санкт-Петербургской Академии наук». Именно в восьмом томе этих «Записок» (с. 128–140) была в 1736 г. опубликована статья Эйлера «Решение одной проблемы, относящейся к геометрии положения» («Solutio problematis ad geometriam situs pertinentis»), едва ли не первая публикация об этом разделе геометрии. Проблема, которую решал Эйлер, состояла в следующем: можно ли прогуляться по в сем кёнигсбергским мостам, не пройдя ни по одному из них дважды? Эйлер доказал, что нельзя. На какой из рисунков (рис. 8, 9 или 10) следует опираться при решении данной задачи? Очевидно, что это не играет никакой роли, потому что задача принадлежит геометрии положения, для которой важно только взаимное расположение элементов, а не их точная форма.
Вторая задача не менее (а в математической среде, пожалуй, даже более) знаменита. Это так называемая проблема четырёх красок. На географических картах административные единицы, имеющие общий участок границы, для удобства принято закрашивать разными цветами. Такую раскраску называют правильной. В 1852 г. при составлении карты деления Англии на графства возник вопрос: каким минимальным числом цветов можно обойтись? Для той конкретной карты хватало четырёх цветов, как хватало их и для всех воображаемых карт, которые удавалось придумать. Но оставалась возможность того, что есть такая карта (скажем, территориально-административного деления Марса), что четырёх цветов оказалось бы недостаточно для её правильной раскраски. Всегда или нет, для любой ли реальной или воображаемой карты хватает четырёх цветов – вот в чем состоит проблема четырёх красок. Наименьшее число цветов, достаточное для правильной раскраски любой мыслимой карты на сфере, называют хроматическим числом сферы. Ясно, что хроматическое число одно и то же для всех сфер. Проблему четырёх красок, следовательно, можно сформулировать так: верно ли, что хроматическое число сферы равно четырём? Но вот обстоятельство, на которое редко обращают внимание: заранее неясно, существует ли хроматическое число сферы вообще. А вдруг можно строить всё более и более сложные карты, раскраска которых требует всё большего и большего числа цветов? В 1890 г. удалось доказать, что для правильной раскраски любой мыслимой карты достаточно пяти цветов. Тем самым было доказано, что хроматическое число сферы существует и что оно не превосходит пяти.
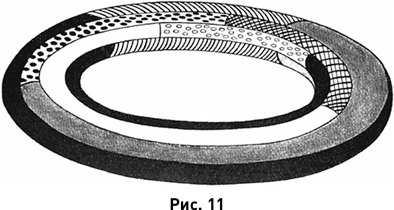
На торе можно нарисовать 7 стран, каждая из которых граничит с 6 другими (рис. 11). Поэтому хроматическое число тора, если оно существует, не может быть меньше 7. Не знаю, когда точно, но к 1940-м гг. уже было доказано, что хроматическое число тора действительно существует и что оно равно 7. Было найдено и хроматическое число поверхности кренделя – 8. В 1954 г. немецкий математик Герхард Рингель (Gerhard Ringel, 1919–2008) опубликовал доказательство существования хроматических чисел для всех замкнутых поверхностей, имеющихся в трёхмерном евклидовом пространстве; более того, для каждой из таких поверхностей он указал такие три последовательных натуральных числа, что одно из них непременно является хроматическим числом данной поверхности. Но проблема четырёх красок оставалась нерешённой.
В 1976 г. было анонсировано, а в 1977 г. изложено доказательство того, что для сферы и плоскости всегда хватает и четырёх цветов; однако оно очень сложно и к тому же опирается на длительные компьютерные вычисления; поэтому не все убеждены в полной корректности этого доказательства. Тем не менее практически все уверены, что хроматическое число сферы и плоскости равно 4.
Всё это факты геометрии положения, где точная форма не имеет значения. Карту можно нарисовать не на плоскости, а на платке, сам же платок смять; сферу можно подвергнуть сжатию, растяжению, сминанию и вообще любой деформации без разрывов и склеиваний, превратить её в поверхность груши, например; тор можно растянуть; крендель – сдавить. Хроматические числа от этого не изменятся.

