Среднеквадратические значения

Для ответа на вопрос Эми нам необходимо воспользоваться «правилом подсчета ошибок» – способом взвесить и свести индивидуальные ошибки в единый показатель общей погрешности. К счастью, такой способ уже существует. Это метод наименьших квадратов, предложенный в 1795 году⁴²⁴³ гением математики Карлом Фридрихом Гауссом, родившимся в 1777 году и вставшим на путь великих открытий в уже очень юном возрасте.

Гаусс предложил правило для оценки вклада индивидуальных ошибок в общую погрешность. Его мера общей погрешности, называемая среднеквадратической ошибкой (MSE), – это среднее значение квадратов индивидуальных погрешностей измерения.

Подробные доводы Гаусса в пользу своего метода измерения общей погрешности выходят далеко за рамки этой книги, а предложенное им решение на первый взгляд неочевидно. Зачем нужны квадраты ошибок? Идея кажется взятой с потолка, даже эксцентричной. И все же, как вы сможете убедиться, она базируется на предположении, с которым вы почти наверняка согласитесь.

Чтобы понять, почему это так, давайте обратимся к проблеме, которая кажется совсем не относящейся к делу, хотя в действительности имеет к нашему вопросу самое прямое отношение. Представьте, что вам вручили линейку и попросили измерить длину прямой с точностью до миллиметра. Проводить замеры разрешено пять раз. Результаты этих замеров представлены на рисунке 5 в виде направленных вниз треугольников, расположенных на прямой.

Рис. 5. Пять замеров одной и той же прямой

Как видите, диапазон результатов пяти замеров составил от 971 до 980 миллиметров. Какой будет ваша самая точная оценка длины этой прямой? У нас есть два очевидных претендента на лучший ответ. Во-первых, это медианное значение: результат, находящийся между двумя наименьшими и двумя наибольшими измерениями. Оно составляет 973 миллиметра. Во-вторых, это среднее арифметическое, или, проще говоря, среднее значение, составляющее в этом примере 975 миллиметров и показанное на рисунке в виде стрелки, направленной вверх. Интуитивно вы, скорее всего, выберете среднее арифметическое и будете правы. Средний показатель более информативен, он зависит от величины значений, тогда как медиана – только от их последовательности.

Между вышеописанной задачей приблизительного подсчета, о пути решения которой у вас имеется четкое интуитивное представление, и задачей измерения общей погрешности, которая нас сейчас интересует, существует тесная связь. На самом деле это две стороны одной медали, потому что самая точная оценка – та, которая минимизирует общую погрешность в имеющихся результатах измерений. Соответственно, если вы правы, интуитивно полагая, что среднее арифметическое – это самая точная оценка, тогда формула для измерения общей погрешности должна подсчитывать среднее арифметическое как значение, для которого погрешность минимизируется.

Среднеквадратическая ошибка такое свойство как раз имеет – и это единственный подобный способ измерения общей погрешности. На рисунке 6 мы показали подсчет MSE в наборе из пяти измерений для десяти возможных целых значений истинной длины прямой. Например, если бы истинное значение равнялось 971, погрешности в пяти измерениях составили бы 0, 1, 2, 8 и 9. Сумма квадратов этих погрешностей равняется 150, а среднее арифметическое – 30. Такое большое число говорит о том, что какие-то измерения довольно далеки от истины. Вы видите, что MSE уменьшается по мере приближения к 975, или среднему арифметическому значению, и снова увеличивается по мере удаления в бóльшую сторону. Нашей лучшей оценкой является среднее арифметическое значение, потому что оно минимизирует общую погрешность.

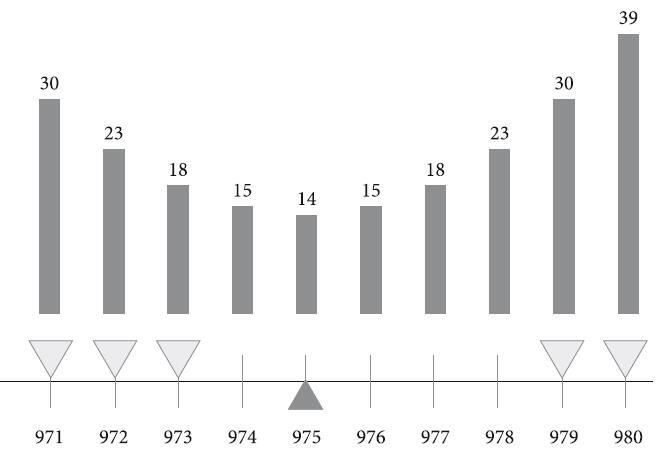
Рис. 6. Среднеквадратическая ошибка для десяти возможных значений истинной длины прямой

Вы также могли заметить, что общая погрешность быстро растет по мере отклонения оценки от среднего арифметического значения. Например, при отклонении оценки всего на 3 миллиметра, от 976 к 979, MSE удваивается. Это ее ключевое свойство: возведение в квадрат придает значительным погрешностям гораздо больший вес, чем незначительным.

Теперь вы понимаете, почему гауссовская формула измерения общей погрешности называется среднеквадратической ошибкой, а сам подход – методом наименьших квадратов. Метод базируется на возведении погрешностей в квадрат, и никакая другая формула не способна поддержать ваше интуитивное предположение, что лучшая оценка – это среднее арифметическое значение.

Другие математики быстро признали преимущества гауссовского метода. Сам же Гаусс среди множества прочих достижений использовал MSE (и другие математические открытия) для решения задачи, которая была не под силу лучшим астрономам Европы: повторного обнаружения Цереры – астероида, который ученые могли наблюдать лишь непродолжительное время, после чего в 1801 году он пропал из виду из-за ярких солнечных бликов. Астрономы пытались рассчитать траекторию движения Цереры, неправильно учитывая погрешность измерения своих телескопов, поэтому так и не обнаружили карликовую планету в точке, на которую указывали их расчеты. Гаусс исправил их вычисления при помощи метода наименьших квадратов. Направив телескопы в точку, указанную Гауссом, астрономы увидели Цереру!

Вскоре метод наименьших квадратов стал применяться учеными в самых различных дисциплинах. Спустя два века он остается стандартным способом оценить погрешность в любых вычислениях, требующих точности. В статистике без взвешивания квадратов погрешностей не обойтись, да и в других областях науки метод наименьших квадратов используется постоянно. Очень скоро мы с вами убедимся, что последствия применения этого подхода могут быть весьма неожиданными.