Уравнения расчета погрешности

Роль смещения и шума в возникновении погрешностей легко обобщить двумя выражениями, которые мы назовем уравнениями расчета погрешности. Первое из этих уравнений раскладывает погрешность однократного измерения на две составляющие, с которыми вы уже знакомы: смещение, или среднюю погрешность, и остаточную «шумную погрешность». Шумная погрешность имеет положительное значение, если погрешность больше, чем смещение, и отрицательное, если меньше. Среднее значение шумных погрешностей равняется нулю. В первом уравнении нет ничего нового:

Погрешность в однократном измерении = Смещение + Шумная погрешность

Второе уравнение расчета погрешности – это разложение на составные части среднеквадратической ошибки, уже знакомой нам меры общей погрешности. При использовании простых алгебраических действий⁴⁴ среднеквадратическая ошибка может быть представлена как сумма квадратов смещения и шума. (Вспомните, что шум – стандартное отклонение в измерениях, идентичное стандартному отклонению шумных погрешностей.) Таким образом:

Общая погрешность (MSE) = Смещение²+ Шум²

Возможно, вид этого уравнения – сумма двух квадратов – напоминает вам известную со школьных лет теорему Пифагора. Как вы, вероятно, помните, в прямоугольном треугольнике сумма квадратов катетов равняется квадрату гипотенузы. Поэтому уравнение расчета погрешности можно визуализировать при помощи трех квадратов, стороны которых образуют стороны прямоугольного треугольника, при этом площади этих квадратов равны соответственно MSE, смещению² и шуму². Рисунок 7 показывает, что MSE (площадь темного квадрата) равняется сумме площадей двух других квадратов. На изображении слева шум больше, чем смещение; на изображении справа смещение больше, чем шум. Однако в обоих случаях MSE одинаковы, а уравнение расчета погрешности применимо к обоим изображениям.

Рис. 7. Два разложения MSE на составляющие

Математическое выражение и его визуализация показывают, что роли смещения и шума в уравнении расчета погрешности идентичны. При определении общей погрешности они взаимонезависимы и равновзвешенны. (Заметьте, что в последующих главах мы прибегнем к похожему разложению на сумму квадратов, анализируя составляющие шума.)

Уравнение расчета погрешности предлагает ответ на практический вопрос, заданный Эми: как изменится общая погрешность, если в одинаковой степени сократить уровень шума или смещения? Ответ на этот вопрос очевиден: в уравнении расчета погрешности смещение и шум взаимозаменяемы, поэтому независимо от того, какой из этих двух показателей мы уменьшим, снижение общей погрешности будет одинаковым. На рисунке 4, где смещение и шум оказались идентичными (по 10 %), их вклад в общую погрешность равнозначен.

Уравнение расчета погрешности определенно говорит в пользу первоначального порыва Эми принять меры по сокращению уровня шума. Каждый раз, когда вы обнаруживаете шум, вы должны постараться его уменьшить! Уравнение указывает на то, что шеф Эми был не прав, предложив подождать до момента, когда можно будет измерить смещение в прогнозах, и только затем принимать решение о дальнейших действиях. При подсчете общей погрешности шум и смещение выступают независимо: выгода от сокращения уровня шума никак не изменится, каким бы при этом ни было смещение.

Эта идея крайне парадоксальна, но при этом принципиально важна. В качестве демонстрации на рисунке 8 показан эффект от одинакового сокращения смещения и шума. Чтобы вам было проще оценить, чего удалось достичь в каждом случае, мы представили первоначальное распределение ошибок (с рисунка 4) в виде пунктирной линии.

В случае А мы исходим из того, что начальник Эми настоял на своем: был определен уровень смещения, затем его сократили вдвое (возможно, предоставив данные исследования прогнозистам, оказавшимся слишком оптимистичными). Уровень шума остался неизменным. На графике сразу заметны улучшения: распределение ошибок целиком сдвинулось в направлении истинного значения.

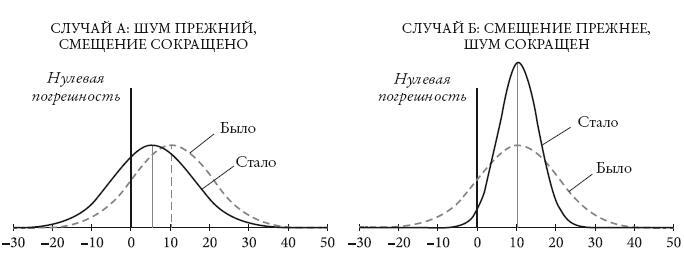
Рис. 8. Распределение ошибок: двукратное сокращение смещения в сравнении с двукратным сокращением шума

В случае Б мы видим, что бы произошло, если бы Эми все же удалось переубедить своего шефа. Уровень смещения не меняется, а шум сокращается вдвое. Парадокс в том, что создается впечатление, что снижение уровня шума только ухудшило ситуацию. Теперь разброс прогнозов гораздо меньше (ниже уровень шума), но они не стали точнее (смещение не изменилось). Если раньше по одну сторону от истинного значения были 84 % прогнозов, теперь там оказались почти все прогнозы (98 %). Кажется, что сокращение шума значительно ухудшило их качество – совсем не похоже на положительные изменения, на которые так надеялась Эми!

Вопреки создавшемуся впечатлению, в обоих случаях общая погрешность уменьшилась одинаково. Иллюзия того, что в случае Б результаты стали хуже, возникает из-за ошибочных интуитивных представлений о смещении. Целесообразной мерой смещения следует считать не то, какой процент ошибок оказывается по разные стороны от нулевой погрешности, а среднюю погрешность – расстояние между наивысшей точкой кривой и истинным значением. В случае Б средняя погрешность не изменилась. Она все еще высока – 10 %, но больше она не стала. Действительно, смещение стало гораздо заметнее, потому что теперь его вклад в общую погрешность весомее (80 % против 50 % ранее). Но это произошло потому, что уменьшился уровень шума. Напротив, в случае А смещение сократилось, а шум остался прежним. В конечном счете MSE одинакова в обоих случаях: равные объемы сокращения шума или смещения оказывают на MSE один и тот же эффект.

Как показывает этот пример, среднеквадратическая ошибка противоречит нашим интуитивным представлениям об оценке прогнозных суждений. Чтобы минимизировать MSE, нужно постараться избежать значительных ошибок. К примеру, при измерении длины эффект от уменьшения погрешности с 11 см до 10 см в 21 раз выше, чем эффект ее сокращения с 1 см до истинного значения. К сожалению, интуитивные представления в этом отношении⁴⁵ почти зеркально противоположны верным: люди всеми силами стремятся получить максимально точный ответ и очень внимательно относятся к небольшим погрешностям, при этом практически игнорируя разницу между двумя значительными ошибками. Даже если вы искренне полагаете, что пытаетесь добиться точности суждения, ваш эмоциональный отклик на результаты может помешать достижению точности в научном понимании.

Конечно же, самым оптимальным решением в этой ситуации будет заняться уменьшением как шума, так и смещения. Поскольку эти величины друг от друга не зависят, бессмысленно выбирать между предложениями Эми Симкин и ее начальника. Если компания GoodSell все же возьмется за сокращение уровня шума, тот факт, что при этом станет очевиднее смещение – а на самом деле его просто невозможно будет не заметить, – может обернуться благом.

Разумеется, при уровне смещения намного больше уровня шума сокращение последнего будет менее приоритетной задачей. Но пример с компанией GoodSell дает нам еще один немаловажный урок. В этой упрощенной модели мы посчитали, что уровни шума и смещения одинаковы. Согласно уравнению расчета погрешности, их вклад в общую погрешность тоже одинаков: 50 % у шума и 50 % у смещения. И все же, как мы заметили, 84 % прогнозистов ошиблись в бóльшую сторону. Требуется именно такой высокий уровень смещения (шесть из семи специалистов ошиблись в одинаковом направлении), чтобы их эффект сравнялся с эффектом шума. Поэтому не стоит удивляться, столкнувшись с ситуациями, когда уровень шума выше, чем уровень смещения.

Мы показали применение уравнения расчета погрешности на единичном примере – только в одном регионе, где GoodSell ведет свою деятельность. Безусловно, всегда желательно проводить ревизию шума сразу на нескольких примерах. Метод при этом не меняется. Уравнение расчета погрешности используют в каждом отдельном случае, и суммарное уравнение получается при подсчете среднего значения среднеквадратической ошибки, квадрата шума и квадрата смещения, разделенных на количество случаев. Для Эми Симкин было бы полезнее получить целый ряд прогнозов по различным регионам от одной или нескольких групп специалистов. Средние результаты дали бы ей более четкую картину смещения и шума в системе прогнозирования компании GoodSell.