Глава 12. Котиковые аналоги или Основы математического моделирования
В предыдущих разделах мы подробно рассмотрели метод регрессионного анализа, который позволяет построить уравнение, описывающее, как различные вещи влияют на настроение котиков. Подобные уравнения входят в группу объектов, называющихся математическими моделями.
Математическая модель – это своего рода аналог котика, который позволяет изучать его поведение без проведения реальных экспериментов. Как правило, это значительно удешевляет исследования.
Все математические модели делятся на функциональные и структурные. Функциональные модели, к которым, к слову, относится регрессионное уравнение, – описывают влияние внешних факторов на котиковое состояние. Например, известная нам модель котикового счастья.

Особенность такой модели в том, что мы подробно не рассматриваем состав этого счастья. Счастье для нас – некий целостный объект, целевая переменная, которая может меняться: прибывать или убывать. А вот структурные модели позволяют описать его компоненты: от удовлетворения базовых котиковых потребностей до котиковой самореализации.
Как правило, функциональные модели записываются с помощью уравнений. А вот структурные могут быть достаточно разнообразными: от таблиц до блок-схем.
Любая математическая модель строится в два этапа. На первом этапе мы прикидываем, какие факторы в принципе могут влиять на котиковое счастье или из каких компонентов оно может состоять. Этот этап называется также построением содержательной модели.

Второй этап включает в себя сбор реальных данных и их математическую обработку. Он называется построением формальной модели. Формальную модель уже можно использовать как аналог реального котика. Изменяя различные параметры этой модели, вы сможете понять, как функционирует котик, не прибегая к опытам над животными.
НЕМАЛОВАЖНО ЗНАТЬ!
Классификация математических моделей
Помимо деления на функциональные и структурные модели есть еще несколько классификаций, о которых полезно знать. В частности бывают модели статические и динамические. Первые описывают состояние котика в какой-то конкретный момент. Вторые же концентрируются непосредственно на изменениях, которые претерпевает котик.
Кроме того, модели делятся на линейные и нелинейные. Линейные модели включают в себя только линейные взаимосвязи, о которых мы подробно говорили в главах про корреляционный и регрессионный анализы. Нелинейные модели могут включать в себя нелинейные взаимосвязи.
Примером здесь может служить полиномиальная регрессия.

Также имеет смысл рассмотреть деление моделей на непрерывные и дискретные. Первые отличаются тем, что в них все переменные имеют бесконечное множество значений. Пример такой переменной – это котиковый размер, измеренный в сантиметрах. Мы можем сказать, что наш котик имеет длину 62 см. А можем – что 62,513987 см. И даже точнее. Если состояние вашего котика измеряется такой переменной, то, чтобы построить функциональную модель, вам необходима линейная регрессия.
Дискретные же модели работают с переменными, которые имеют ограниченное количество значений. Например, тот же размер, но имеющий только три значения: маленький, средний и большой. Построить модели с дискретными целевыми переменными, в частности, позволяют логистическая регрессия и дискриминантный анализ.
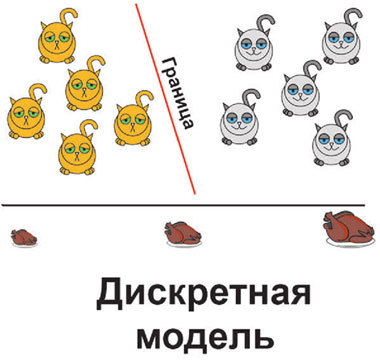
Впрочем, на практике большинство моделей относятся к смешанным типам – в них встречаются как дискретные, так и непрерывные переменные, а линейные взаимосвязи вполне могут сочетаться с нелинейными.
Глава 13. Разновидности котиков или Основы кластерного анализа
Из предыдущих разделов мы узнали, как определить, какие факторы делают наших котиков счастливыми. В этом нам помогли регрессионный и дискриминантный анализы. Зная значения этих факторов, мы можем предсказать, будет ли тот или иной котик счастливым или несчастным. Иными словами, мы можем рассортировать котиков по классам, т. е. классифицировать их.
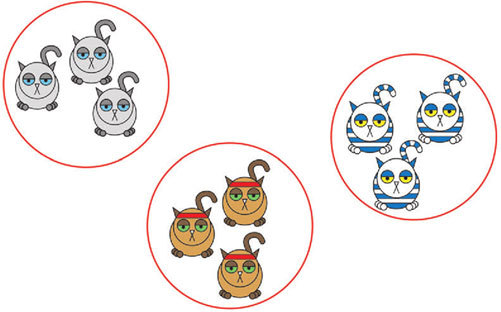
Вообще, задача классификации является крайне важной практически для всех наук, изучающих котиков. Но довольно часто мы не имеем никакого понятия даже о том, на какие группы делятся котики. Ведь котики очень разные. Поэтому существуют методы, которые позволяют не только рассортировывать котиков на группы, но и выделять сами эти группы. И все вместе они называются кластерным анализом.
В первом приближении у нас могут возникнуть две ситуации. Первая – мы знаем, на сколько групп у нас должны делиться котики, но не имеем понятия, где эти группы находятся. Вторая – мы не знаем итоговое количество групп. Со второго случая мы, пожалуй, и начнем.
Рассмотрим самый простой пример. Предположим, что мы захотели поделить наших котиков по размеру. Очевидно, что чем больше два котика похожи друг на друга, тем больше шансов, что они окажутся в одной группе. Чтобы понять степень похожести, надо просто найти разность между размерами – чем она меньше, тем более похожими являются наши котики.
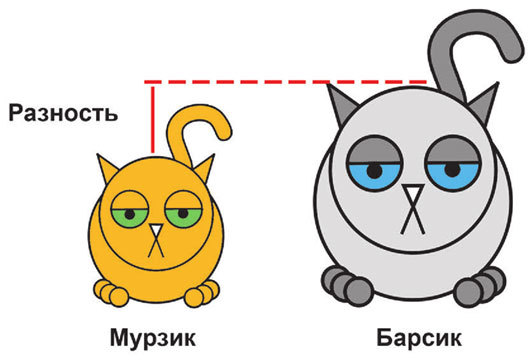
Итак, мы вычисляем все возможные разности между размерами котиков. Далее пара самых похожих котиков объединяется в группу (или кластер). Затем мы вновь вычисляем разности. А затем опять объединяем самых похожих. И так происходит до тех пор, пока у нас все котики не объединятся в один большой кластер.
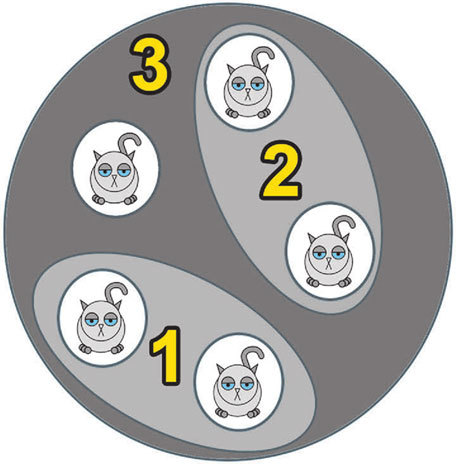
Этот алгоритм относится к методам иерархической кластеризации. Их довольно много, но каждый из них обладает следующими свойствами.
1. Эти методы могут работать с большим количеством переменных – вы можете брать и размер, и степень пушистости, и длину коготков, и прочие котиковые признаки одновременно.
2. На основе этих признаков вы вычисляете степень похожести котиков (чаще используется термин расстояние).
3. Котики последовательно объединяются в группы. Это может происходить так, как было описано выше (так называемый «метод ближайшего соседа»), а может и по другим принципам.
4. По итогу вы получаете график, называемый дендрограммой. По ней вы можете определить, на какие группы делятся ваши котики и какие котики к какой группе принадлежат. Единственное – если котиков очень много, воспринимать такую дендрограмму довольно сложно.
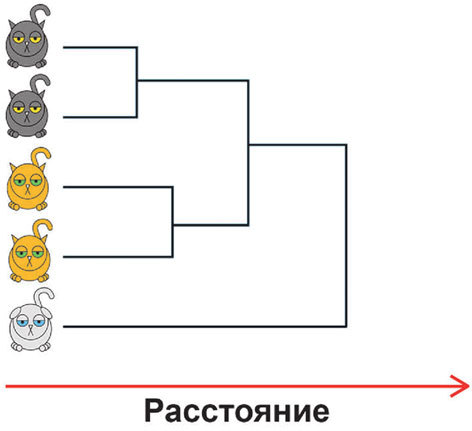
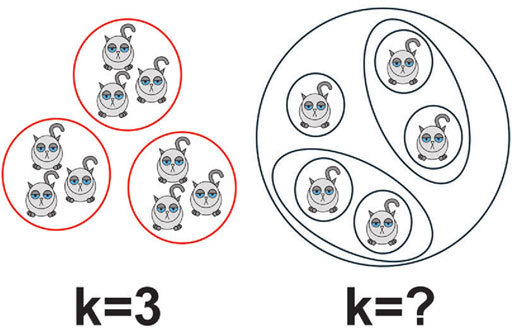
Напомним, что иерархический кластерный анализ позволяет вам разбить котиков на группы, когда вы не знаете, сколько у вас их должно получиться. А если знаете, то более адекватным будет использование метода k-средних.
Идея достаточно проста. Предположим, вы подозреваете, что все котики делятся на три различающиеся размером группы. Тогда у каждой группы существует свой представитель, который обладает самым типичным для группы размером. Такой котик называется центроидом. И основная задача алгоритма k-средних – найти, каким именно размером эти центроиды обладают.
Происходит это пошагово. На первом этапе мы произвольно расставляем центроиды.
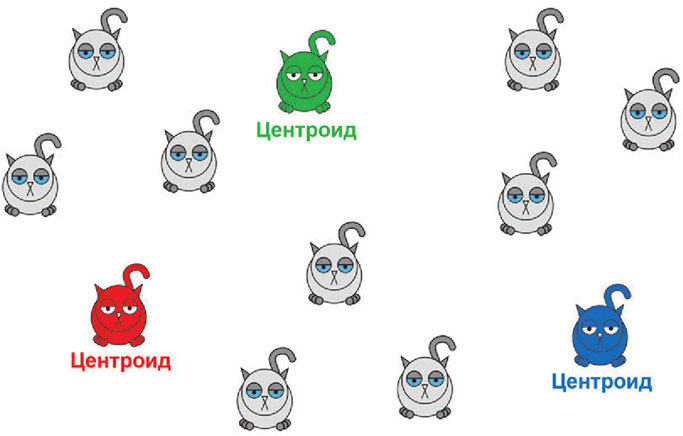
На втором этапе вычисляются расстояния от каждого котика до каждого центроида.
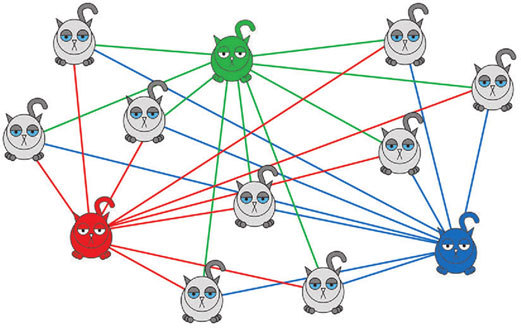
На третьем – определяем принадлежность котиков к тому или иному центроиду. Иными словами – смотрим, какой котик к какому центроиду ближе.
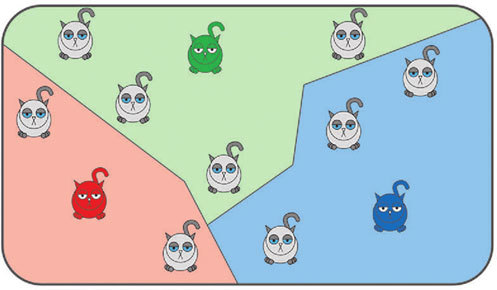
И на четвертом этапе мы вычисляем средний размер котиков при каждом центроиде. И центроид перемещается в этот средний размер.
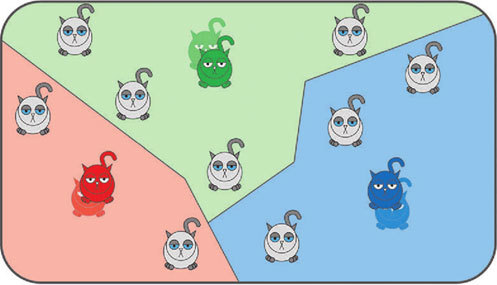
А потом алгоритм повторяется со второго шага. Происходит это потому, что некоторые котики перебегают от одного центроида к другому, вследствие чего положение центроидов также будет меняться.
Происходит это ровно до тех пор, пока после очередного повторения положение центроидов останется неизменным.
Важно отметить следующие вещи. Во-первых, k-средних может работать сразу по нескольким переменным. Для этого, как и для иерархического кластерного анализа, вычисляется расстояние, но уже не между отдельными котиками, а между конкретным котиком и центроидом.
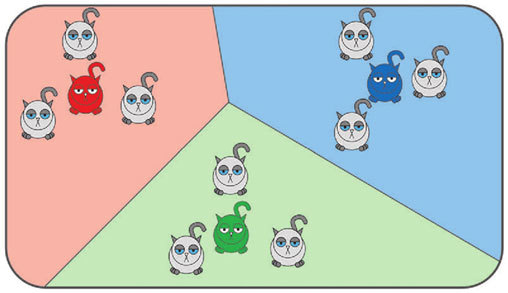
Во-вторых, результат k-средних сильно зависит от начального положения центроидов. Некоторые такие положения могут приводить к довольно-таки бредовым результатам. Поэтому k-средних лучше проводить несколько раз подряд. Кстати, если вы при этом каждый раз получаете разные результаты, стоит задуматься о смене количества групп.
НЕМАЛОВАЖНО ЗНАТЬ!
Метрики расстояний
Конкретные результаты кластерного анализа во многом зависят от того, какую метрику расстояния вы выбрали. А их существует несколько.
Самая простая из них – эвклидово – есть просто кратчайший путь между двумя точками.
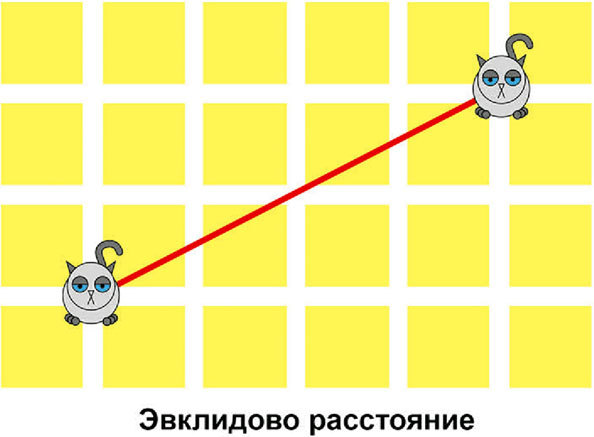
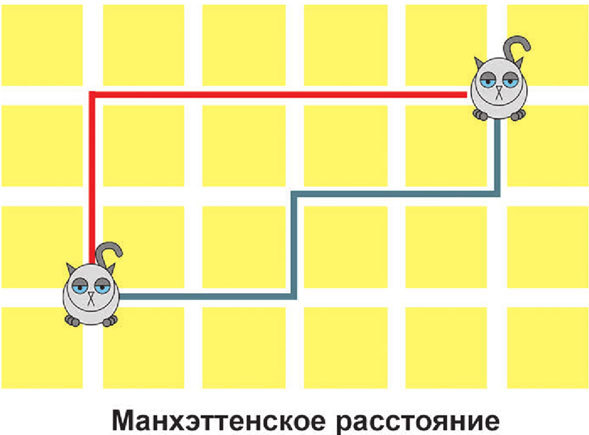
Иногда вместо него используют так называемое Манхэттенское расстояние. Названо оно было в честь Манхэттена, а точнее – в честь его планировки. Прогуливаясь по Манхэттену, вы не можете попасть из точки А в точку Б по кратчайшему пути. Если только вы не можете проходить сквозь стены, вам обязательно придется идти вдоль его параллельно-перпендикулярных улиц.
Заметим, что синий и красный пути абсолютно одинаковы. Манхэттенское расстояние лучше использовать в случаях, если вы подозреваете, что в вашей выборке есть выбросы.
Последняя наиболее часто используемая метрика – это расстояние Чебышева. Она немного похожа на Манхэттенское расстояние. Но только чуть-чуть. Потому что его можно определить как максимальное расстояние, которое котику нужно будет пройти вдоль одной улицы.