Глава 14. О котиковом характере или Основы факторного анализа
Безусловно, каждый котик – уникальная и сложная личность. У него есть индивидуальные желания и предпочтения, а также собственный взгляд на мир и свое место в нем. Впрочем, некоторые психологические особенности (например, любовь к еде) являются общими для всех котиков.

Однако, к большому сожалению, в отличие от всяких внешних признаков (к примеру таких, как размер или пушистость), психологические особенности не так просто измерить, поскольку их нельзя увидеть. И потому мы нуждаемся в специальных методах для их выявления.
В качестве примера вспомним, что большинство котиков склонны точить когти о диван и время от времени царапать своих хозяев. При этом мы наблюдаем линейную положительную взаимосвязь между этими явлениями – котики, которые дерут большее количество диванов, склонны оставлять большее количество царапин.

Глядя на эту взаимосвязь, мы можем предположить, что за этими склонностями стоит некоторая скрытая причина, которая вполне может являться особой чертой котикового характера. Назовем ее царапучестью. Чем выше царапучесть, тем больше котики склонны царапать диваны и людей.
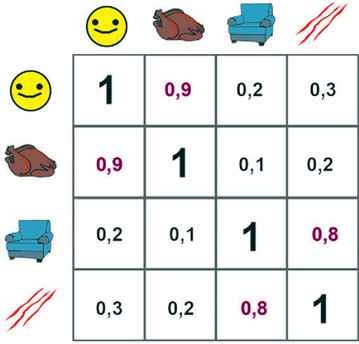
Выявить такие скрытые причины (или факторы) помогает факторный анализ, который проходит в несколько этапов. Во-первых, рассчитывается корреляционная матрица между всеми переменными, которые вы замерили: размером, количеством еды, склонностью царапать людей и т. д.
Во-вторых, переменные, которые коррелируют между собой, заменяются факторами. Чтобы понять, как это происходит, обратимся к рисунку.
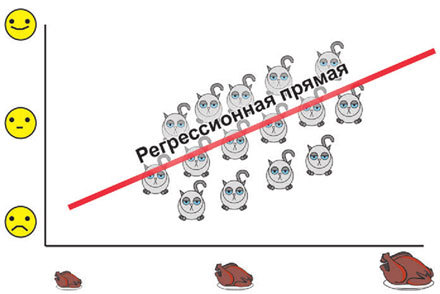
На нем уже знакомая нам линейная взаимосвязь, которая описывается регрессионной прямой. Давайте теперь повернем наш рисунок таким образом, чтобы эта прямая лежала по горизонтали, и проведем прямую, перпендикулярную регрессионной.
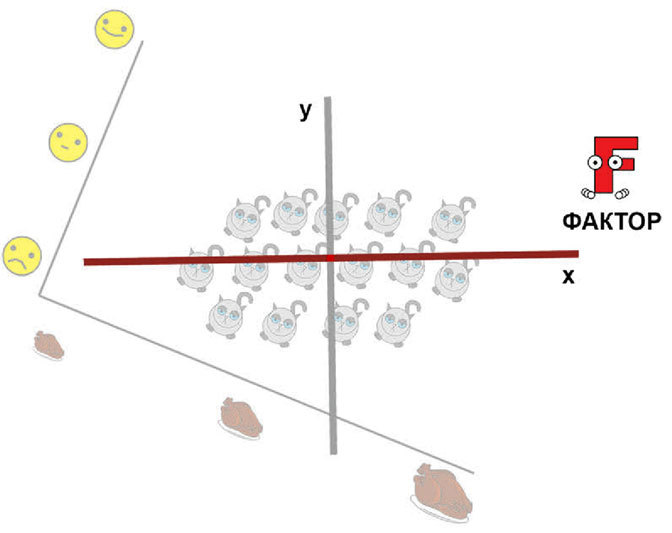
У нас получилась новая система координат. При этом большая часть котиков лежит вдоль оси Х. Эта ось и будет являться фактором, заменяющим как количество поглощаемой пищи, так и котиковое счастье.
В итоге мы получаем вот такую таблицу, которая называется факторной матрицей. В каждой ячейке такой таблицы – коэффициент корреляции между одним из факторов и конкретной переменной. Называется он факторной нагрузкой. Сумма коэффициентов корреляции для каждого фактора называется собственным значением.
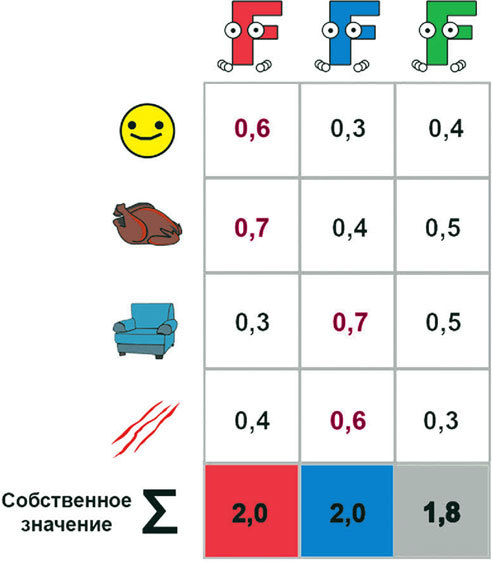
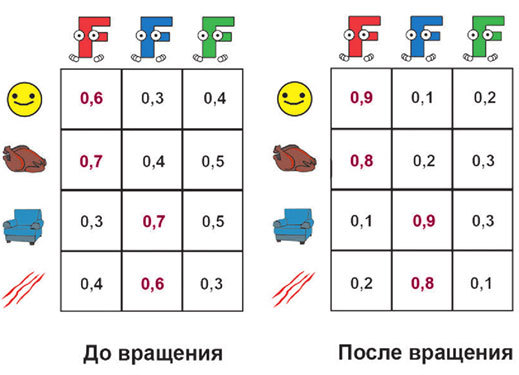
Далее происходит так называемая процедура вращения. Цель ее заключается в том, чтобы большие коэффициенты корреляции в факторной матрице стали еще больше, а маленькие – еще меньше. Это значит, что каждый фактор будет связан только с определенной группой переменных и ни с какими другими.
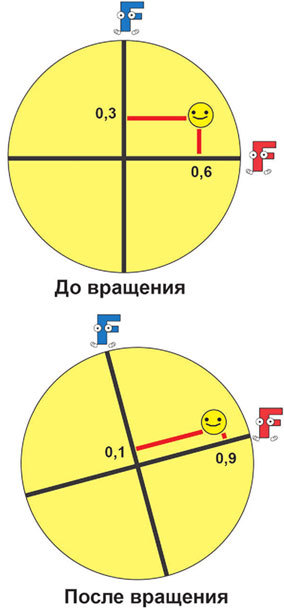
Чтобы прояснить, как работает вращение, также обратимся к рисунку. На нем изображена переменная «Счастье», которая коррелирует с первым и вторым факторами. Координаты «Счастье» – это коэффициенты корреляции между ним и факторами.
Если мы будем вращать окружность против часовой стрелки, то координаты «Счастья» будут меняться. Соответственно, оно будет больше коррелировать с первым фактором и меньше – со вторым.
Вращение бывает двух видов – ортогональное и косоугольное. В первом случае получившимся факторам запрещается коррелировать между собой, а во втором – нет.
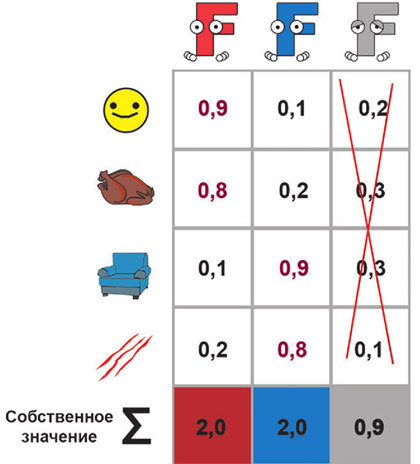
Предпоследняя процедура – это отсеивание лишних факторов, которые слабо связаны с первоначальными переменными. Для этого существует два способа. Первый (называемый критерием Кайзера) заключается в том, что мы отбраковываем все факторы с собственным значением ниже 1.
Второй способ называется методом каменистой осыпи (или критерием Кеттелла). Для того чтобы им воспользоваться, необходимо построить график собственных значений. На горизонтальной оси этого графика располагаются факторы, а на вертикальной – их собственные значения. На определенной точке этого графика происходит перегиб. И все факторы, которые находятся за этой точкой, отсеиваются.
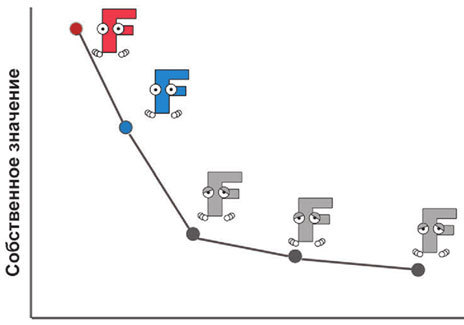
И наконец последний шаг – это придумать название получившимся факторам. Этот шаг является довольно нетривиальным – подчас он вызывает наибольшие затруднения. Но если вы успешно преодолеете его, то у вас на руках может оказаться довольно неплохая структурная модель котикового характера. В нашем случае первый фактор будет называться «жизнерадостностью», а второй – «царапучестью».
НЕМАЛОВАЖНО ЗНАТЬ!
Применение факторного анализа
Изначально факторный анализ был разработан психологами для изучения способностей и личностных качеств. Однако со временем область применения данного метода существенно расширилась.
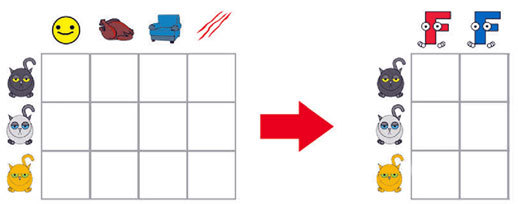
Первая большая проблема, которую позволяет решить факторный анализ, это сокращение количества переменных. Как правило, серьезные исследования подразумевают сбор большого количества данных. Настолько большого, что в них бывает очень трудно разобраться. В этом случае факторный анализ позволяет уменьшить их количество за счет замены изначальных переменных факторами.
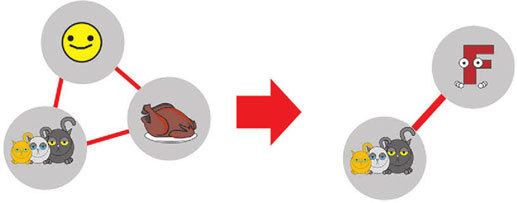
Вторая задача, требующая применения факторного анализа, это устранение мультиколлинеарности из регрессионных моделей. Напомним, что эта проблема заключается в том, что если две или более переменные взаимосвязаны между собой, результаты регрессионного анализа будут крайне ненадежными. Поэтому такие переменные требуется удалить из анализа. И один из путей – это замена таких переменных факторами.

