Глава 4
√2
Перед началом концерта музыканты настраивают инструменты по одной ноте, чтобы добиться гармоничного звучания. Однако это невозможно. Скоро мы увидим почему.
Рациональные числа
Целые числа прекрасно ладят с тремя простейшими арифметическими действиями – со сложением, вычитанием и умножением. Мы производим эти операции над двумя целыми числами и получаем целое же число. А вот деление одного целого числа на другое может привести к дробному результату.
Числа, представляющие собой результат деления целого числа на целое, называют рациональными. Например, 1,5 – это рациональное число, потому что равно 3/2.
Целое число 3 рациональное, потому что 3 = 3/1 (а еще 6/2, 12/4 и т. д.). Все целые числа – рациональные.
Целые числа ладят с тремя арифметическими действиями, а рациональные числа – со всеми четырьмя. Сумма, разность, произведение и частное рациональных чисел всегда будут рациональным числом (с привычной оговоркой о неправомерности деления на ноль).
Рациональные числа пригодны для описания повседневной жизни. Величины, которые мы измеряем, – вес, интенсивность звука, расстояние, цена, температура, время, численность населения, радиочастоты – выражаются рациональными числами.
Но если рациональные числа удобны для работы и над ними можно осуществлять арифметические операции, зачем нам другие числа?
Можно задаться более фундаментальным вопросом: существуют ли другие числа?
Диагональ квадрата
Каково расстояние между противоположными вершинами квадрата? Позже, в главе 14, мы обсудим решение этой задачи. Сейчас же достаточно знать, что длина диагонали квадрата 1 × 1 равна √2
Если умножить число √2 само на себя (другими словами, возвести в квадрат), мы получим 2. Посчитайте приблизительное значение √2 на калькуляторе. А теперь давайте посмотрим, можно ли приблизиться к этому числу с помощью ручки и бумаги.
Начнем с того, что, если возвести в квадрат 0, получится 0, а если возвести в квадрат 1, получится 1. Наша цель 2, а найденные числа меньше. С другой стороны, если возвести в квадрат 2, мы получим 4, а если возвести в квадрат 3, получим 9. Это больше, чем нам нужно.
1² – слишком ма́ло, 2² – слишком много. Попробуем найти величину между 1 и 2, перемещаясь с шагом 0,1, как показано в таблице.

Легко заметить: 1,4 слишком мало для квадратного корня из двух, а 1,5 – слишком велико. Следовательно, √2 лежит между этими двумя величинами.
Продолжим в том же духе. Будем возводить в квадрат числа между 1,4 и 1,5, двигаясь с шагом 0,01. Мы обнаружим, что 1,41² = 1,9881, а 1,42² = 2,0164. Из этого можно сделать умозаключение, что 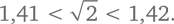
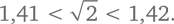
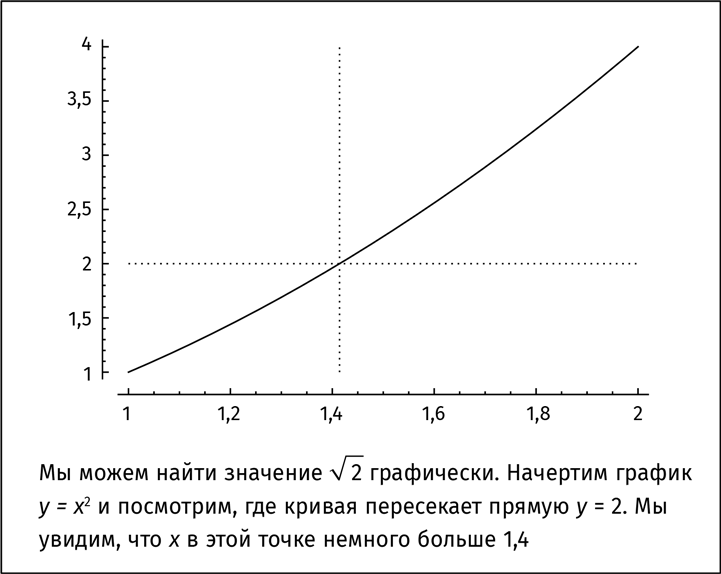
Мы можем двигаться таким образом все дальше и дальше, приближаясь к √2
Рано или поздно мы либо успокоимся (достигнув числа, фантастически близкого к  либо почувствуем отчаяние (увидев, что никогда не сможем точно вычислить √2
либо почувствуем отчаяние (увидев, что никогда не сможем точно вычислить √2
 либо почувствуем отчаяние (увидев, что никогда не сможем точно вычислить √2
либо почувствуем отчаяние (увидев, что никогда не сможем точно вычислить √2Но что означает это «точно»?
За границами рационального
Разумный способ определить точное значение числа – представить его в виде рационального числа, то есть отношения двух целых чисел. Если бы мы сумели представить √2 в виде дроби  где a и b – целые числа, мы бы нашли его точное значение.
где a и b – целые числа, мы бы нашли его точное значение.
 где a и b – целые числа, мы бы нашли его точное значение.
где a и b – целые числа, мы бы нашли его точное значение.Увы, но такое невозможно. Однако это нужно доказать.
Теорема. √2 не является рациональным числом.
Будем идти от противного, как и в главе 1, где мы подсчитывали количество простых чисел. Предположим, что √2 – рациональное число. Если это допущение приведет к абсурдным выводам, значит, оно несостоятельно.
Итак, приступим. Если √2 – рациональное число, его можно выразить в виде отношения двух целых чисел:
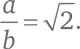
Возведем обе части тождества в квадрат:
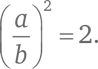
Раскроем скобки:
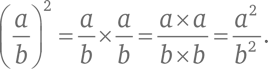
Таким образом:
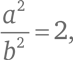
или:
2b² = a². (С)
Если a – целое число, мы можем разложить его на простые множители, причем (согласно основной теореме арифметики) одним-единственным способом:
a = p1 × p2 × … × pn.
Проделаем аналогичную процедуру с b:
b = q1 × q2 × … × qm.
Следовательно, левую часть равенства (С) можно представить в таком виде:
2b² = 2 × (q1 × q2 × … × qm)² = 2 × (q1 × q1) × (q2 × q2) × … × (qm × qm).
Несложно заметить, что 2b² раскладывается на нечетное число простых множителей.
Аналогично поступаем с правой частью (С):
a² = (p1 × p2 × … × pn) ² = (p1 × p1) × (p2 × p2) × … × (pn × pn).
В отличие от 2b², выражение a² раскладывается на четное число простых множителей.
Подытожим. В соответствии с нашим предположением 2b² = a². Это означает, что некоторое число одновременно можно разложить на четное и нечетное количество простых множителей. Но это противоречит основной теореме арифметики.
Мы пришли к невозможному выводу. Таким образом, наша изначальная посылка была ошибочна. Следовательно, √2 не является рациональным числом.
Такие числа, как √2 называют иррациональными. Рациональные числа хороши для операций с физическими величинами, но их недостаточно для всех математических величин. Длина диагонали квадрата 1 × 1 – иррациональное число.
Конструктивные числа
Начав с числа 1 и шаг за шагом проделывая операции сложения, вычитания и умножения, мы можем получить любое целое число, но и только. Если мы добавим операцию деления, нам откроются все рациональные числа, но ими же мы и будем ограничены.
Если мы введем операцию извлечения квадратного корня, то получим числа, которые не являются отношением целых чисел. Например:
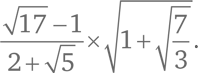
Для удобства мы будем называть конструктивными такие числа, которые можно получить с помощью числа 1 и пяти операций – сложения, вычитания, умножения, деления и извлечения квадратного корня – с привычными оговорками: нельзя делить на ноль и извлекать корень из отрицательных величин.
Разумеется, возникает вопрос: все ли числа конструктивные?
Древние греки усматривали магическую внутреннюю связь между арифметикой и геометрией. Эта связь подтверждалась операциями с использованием двух инструментов: линейки без делений и циркуля. Возьмем отрезок единичной длины; какова может быть длина отрезков, построенных на его основе с помощью карандаша, линейки без делений и циркуля?
Складывать и вычитать отрезки просто. Пусть у нас есть отрезки длиной a и b. С помощью линейки мы продлеваем первый отрезок. Ставим иглу циркуля в начало второго отрезка, а острие карандаша на другой ножке циркуля – в конец отрезка. После этого мы перемещаем иглу в конец первого отрезка и отмечаем точку на продленной линии. Так мы находим сумму двух отрезков. Что касается вычитания, оно будет означать не приращение, а укорочение отрезков.
Дальше дело пойдет несколько сложнее, но мы вполне способны умножать, делить и даже извлекать квадратные корни из длин отрезков с помощью линейки без делений и циркуля.
Да, это так: с помощью двух простейших инструментов мы можем найти длины, равные всем положительным конструктивным числам!
Было время, когда греки думали, что все числа рациональные, но пифагорейцы доказали, что это не так.
Однако грекам было непросто расстаться с верой в связь арифметики и геометрии. В основе этой веры лежали представления об эстетике. Неужели не все числа можно выразить с помощью линейки без делений и циркуля?
Эта вера подкреплялась решениями двух из трех знаменитых древнегреческих геометрических задач. Наиболее известна задача о трисекции угла: с помощью линейки без делений и циркуля нужно поделить заданный угол на три равных угла.
Менее известны две другие головоломки:
• Удвоение куба. Необходимо найти длину ребра куба, чей объем в два раза больше заданного. Если длина ребра первого куба – единица, это равносильно построению отрезка длиной 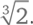
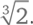
• Квадратура круга. Необходимо построить квадрат, чья площадь равна площади заданного круга. Если радиус круга равен единице, его площадь равна π. Тогда сторона квадрата будет равна 

Понадобилось две тысячи лет, чтобы понять: эти задачи неразрешимы. Ни 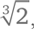 ни
ни 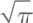 не являются конструктивными числами. Решая проблему трисекции угла, мы сталкиваемся с тем фактом, что некоторая величина (косинус 20°) не является конструктивным числом.
не являются конструктивными числами. Решая проблему трисекции угла, мы сталкиваемся с тем фактом, что некоторая величина (косинус 20°) не является конструктивным числом.
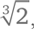 ни
ни 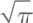 не являются конструктивными числами. Решая проблему трисекции угла, мы сталкиваемся с тем фактом, что некоторая величина (косинус 20°) не является конструктивным числом.
не являются конструктивными числами. Решая проблему трисекции угла, мы сталкиваемся с тем фактом, что некоторая величина (косинус 20°) не является конструктивным числом.Существование неконструктивных чисел опровергает связь между арифметикой и геометрией, гревшую сердца древним грекам, которые решали задачи на построение с линейкой без делений и циркулем.
Музыкальная гармония
Если музыканты перед концертом не настроили инструменты, возникает акустический диссонанс: музыка становится неблагозвучной.
Когда на двух инструментах берут одинаковые ноты, акустическая частота звуковых волн оказывается одинаковой. Рассогласованность же действует слушателю на нервы. Впрочем, можно брать и разные ноты, и музыка все равно будет ласкать слух, если эти ноты гармонируют друг с другом. Но как достичь гармонии? Что именно нам приятно слышать?
Этот вопрос волновал еще древних греков. Они выяснили, что, если акустические частоты соотносятся как малые целые числа (например, 2 и 3), сочетание нот ласкает слух. Так был открыт первый музыкальный строй (по легенде, его создал Пифагор). Подбирая частоты для нот, важно выполнить главное требование: частоты нот, находящихся на противоположных концах октавы, должны соотноситься примерно как 2:1. Ради гармоничных звуков древние греки подбирали ноты так, чтобы парное соотношение частот до и фа, а также до и соль выражалось малыми целыми числами. В пифагорейском варианте соотношение между частотами соседних нот было равно 9/8 для целого тона (например, между до и ре) и 256/243 для полутона (например, между ми и фа).
Вот весь пифагоров строй:
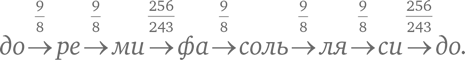
Из этого соотношения можно посчитать соотношение, скажем, между частотами нот до и фа. Мы получим частоту фа, если умножим частоту до на
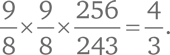
Акустические частоты, соотносящиеся как 4:3, прекрасно звучат вместе.
Мы можем визуализировать звуковые волны, возникающие, когда до и фа звучат вместе. Это будет выглядеть примерно так:

А частота ноты ля окажется немножко выше, звуковая волна будет выглядеть так:

Разница, заметная для глаза, заметна также и для слуха; вы видите диссонанс.
Недостаток пифагорова строя в том, что широко распространенное мажорное трезвучие до мажор – до-ми-соль – звучит как диссонанс; соотношение частот достаточно сложное.
Спустя много веков были найдены другие варианты. Например, так называемый чистый строй, или натуральный строй, выглядит так:
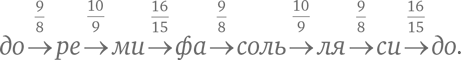
В этом варианте частоты до, ми и си прекрасным образом соотносятся как 4:5:6. Но полный тон от до до ре звучит иначе, чем другой полный тон от ре до ми.
И у пифагорова строя, и у натурального строя есть еще один серьезный изъян: если ансамбль исполняет произведение в тональности, скажем, до мажор, а затем музыканты должны переключиться на тональность фа, инструменты придется перенастраивать. Это довольно затруднительно для лютниста, невероятно сложно для клавикордиста и совершенно нереально для тех, кто играет на деревянных духовых.
Исправить изъян можно, если создать музыкальный строй, действующий одинаково хорошо во всех тональностях. Это накладывает два условия:
1. Частоты нот на противоположных концах октавы должны соотноситься как 2:1;
2. Если ноты отделены полутоном, соотношение их частот должно быть таким же, как у остальных полутонов октавы (например, соотношение частот до и ми-диез равно соотношению частот до-диез и ре). Всего в октаве двенадцать полутонов: до, до-диез, ре, ми, ми-диез, фа, фа-диез, соль, соль-диез, ля, ля-диез и си.
Если соотношение частот любых двух соседних нот равно r (условие 2), а соотношение частот двенадцатой и первой ноты равно 2 (условие 1), то r12 = 2. Следовательно,
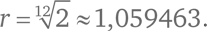
Если настроить музыкальные инструменты таким образом, чтобы соотношение частот соседних нот в октаве было равно  не придется перенастраиваться при переходе в другую тональность. Этот музыкальный строй называют равномерно темперированным, и сегодня им пользуются все профессиональные музыканты.
не придется перенастраиваться при переходе в другую тональность. Этот музыкальный строй называют равномерно темперированным, и сегодня им пользуются все профессиональные музыканты.
 не придется перенастраиваться при переходе в другую тональность. Этот музыкальный строй называют равномерно темперированным, и сегодня им пользуются все профессиональные музыканты.
не придется перенастраиваться при переходе в другую тональность. Этот музыкальный строй называют равномерно темперированным, и сегодня им пользуются все профессиональные музыканты.К сожалению, число 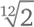 иррационально. Иными словами, соотношение частот двенадцати нот в равномерно темперированном строе (за исключением начала и конца октавы) не может быть выражено через соотношение целых чисел. Соотношение частот до и соль в таком случае равно не 3:2, а примерно 1,4983 (число принято округлять до 1,5).
иррационально. Иными словами, соотношение частот двенадцати нот в равномерно темперированном строе (за исключением начала и конца октавы) не может быть выражено через соотношение целых чисел. Соотношение частот до и соль в таком случае равно не 3:2, а примерно 1,4983 (число принято округлять до 1,5).
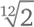 иррационально. Иными словами, соотношение частот двенадцати нот в равномерно темперированном строе (за исключением начала и конца октавы) не может быть выражено через соотношение целых чисел. Соотношение частот до и соль в таком случае равно не 3:2, а примерно 1,4983 (число принято округлять до 1,5).
иррационально. Иными словами, соотношение частот двенадцати нот в равномерно темперированном строе (за исключением начала и конца октавы) не может быть выражено через соотношение целых чисел. Соотношение частот до и соль в таком случае равно не 3:2, а примерно 1,4983 (число принято округлять до 1,5).Как это звучит? Сейчас почти все музыкальные инструменты настраивают по равномерно темперированному строю, и они ласкают наш слух. Но что мы теряем?
Вот как выглядит звуковая волна для трезвучия до мажор. В первом варианте частоты нот соотносятся как 4:5:6, во втором подобраны в соответствии с равномерно темперированным строем. Первый вариант выглядит (и звучит!) гораздо гармоничнее.
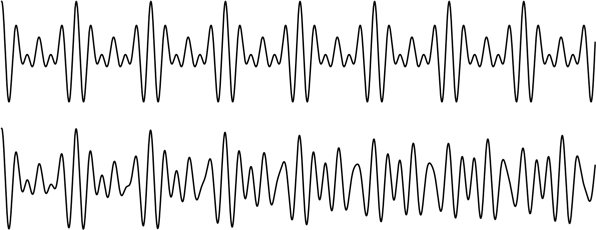
Преимущество равномерно темперированного строя состоит в том, что в нем нет необходимости постоянно перенастраивать музыкальные инструменты. Но есть один инструмент, способный менять тональность мгновенно: человеческий голос.
Вокальные ансамбли без инструментального сопровождения (например, «парикмахерские» квартеты) не нуждаются в равномерно темперированном строе и берут ноты, соотношение частот которых можно выразить целыми числами. И мы слышим чудесные хорошо резонирующие звуки.
Назад: Глава 3 0,99999999999…
Дальше: Глава 5 i

