Глава 5
i
Еще одна головоломка квадратного корня
В главе 4 мы поразмышляли над «точным» значением числа √2 и пришли к выводу, что его нельзя выразить в виде соотношения двух целых чисел и, следовательно, оно иррационально. Тем не менее мы можем найти его значение с невероятной точностью.
Число √2 не относится к рациональным числам, однако нас не мучает вопрос, существует ли такое число, что x² = 2. Несмотря ни на что, √2 имеет законную прописку где-то между 1,41 и 1,42. Это пример действительного числа. Оно может быть выражено так:
± XXXX, XXXXXXXXXX…
Символом X помечены разные цифры. Число может быть положительным или отрицательным (знак + перед числом ставить не принято), количество цифр до запятой конечно, количество цифр после запятой бесконечно. Скажем, 1⅔ можно записать так:
1,666666666666…
Такие числа, как 3/4, в десятичной системе счисления записываются с конечным числом цифр после запятой (0,75), но ничто не мешает прикрутить справа бесконечное количество нулей: 0,7500000000…
Таким образом, 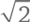 – реальное число, просто иррациональное. Точнее говоря, существует такое число, что x² = 2. Точно так же существует такое число, что x² = 3, а именно
– реальное число, просто иррациональное. Точнее говоря, существует такое число, что x² = 2. Точно так же существует такое число, что x² = 3, а именно 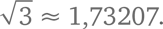 И так далее… Или нет?
И так далее… Или нет?
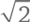 – реальное число, просто иррациональное. Точнее говоря, существует такое число, что x² = 2. Точно так же существует такое число, что x² = 3, а именно
– реальное число, просто иррациональное. Точнее говоря, существует такое число, что x² = 2. Точно так же существует такое число, что x² = 3, а именно 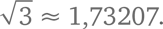 И так далее… Или нет?
И так далее… Или нет?Всякое ли уравнение x² = a имеет решение? Если a – положительное действительное число (или ноль), тогда решение равно 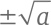 и ответ можно записать в виде десятичного числа сколько угодно точно. Если мы изобразим график y = x² – a (для любого квадратного уравнения он представляет собой параболу), решением будут те точки, где кривая пересекает ось абсцисс, или ось x. Иными словами, это такие значения x, при которых x² = a. На первом рисунке вы можете видеть графики y = x² – 3 и y = x² – 7. Первая парабола пересекает ось абсцисс при
и ответ можно записать в виде десятичного числа сколько угодно точно. Если мы изобразим график y = x² – a (для любого квадратного уравнения он представляет собой параболу), решением будут те точки, где кривая пересекает ось абсцисс, или ось x. Иными словами, это такие значения x, при которых x² = a. На первом рисунке вы можете видеть графики y = x² – 3 и y = x² – 7. Первая парабола пересекает ось абсцисс при  вторая парабола – при
вторая парабола – при 
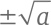 и ответ можно записать в виде десятичного числа сколько угодно точно. Если мы изобразим график y = x² – a (для любого квадратного уравнения он представляет собой параболу), решением будут те точки, где кривая пересекает ось абсцисс, или ось x. Иными словами, это такие значения x, при которых x² = a. На первом рисунке вы можете видеть графики y = x² – 3 и y = x² – 7. Первая парабола пересекает ось абсцисс при
и ответ можно записать в виде десятичного числа сколько угодно точно. Если мы изобразим график y = x² – a (для любого квадратного уравнения он представляет собой параболу), решением будут те точки, где кривая пересекает ось абсцисс, или ось x. Иными словами, это такие значения x, при которых x² = a. На первом рисунке вы можете видеть графики y = x² – 3 и y = x² – 7. Первая парабола пересекает ось абсцисс при  вторая парабола – при
вторая парабола – при 
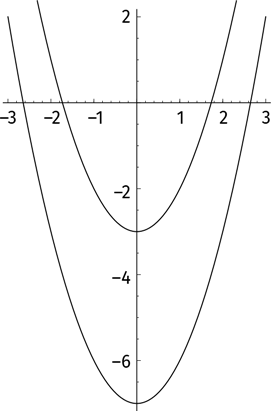
Вопрос кардинально меняется, когда мы ищем такое число, что x² = –1. А существует ли оно в принципе? Если возвести в квадрат положительное число, ответом будет положительное число, скажем 5² = 5 × 5 = 25 > 0. Если возвести в квадрат отрицательное число, результат снова будет положительным числом: (–5)² = (–5) × (–5) = 25 > 0. Если возвести в квадрат ноль, получится ноль. Наше положение выглядит безнадежно.
Мы испытаем еще большее отчаянье, когда нарисуем график уравнения y = x² + 1 и увидим, что парабола нигде не пересекает ось абсцисс.
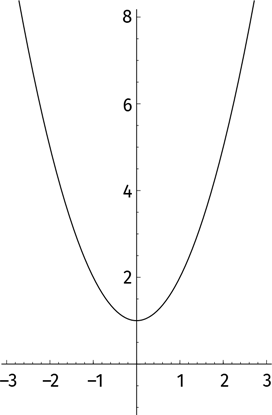
Есть искушение сдаться и объявить: «Нельзя извлекать квадратные корни из отрицательных чисел». На самом деле нам просто не хватает воображения. Да, не существует ни одного действительного числа, удовлетворяющего условию x² = –1, но, возможно, есть какие-то другие?
Мнимые числа
Решение на редкость просто. Раз нет такого действительного числа, что x² = –1, то мы просто создадим новое число, назовем его i и поставим условие i² = –1.
Конечно, в голове сразу зазвучит сигнал тревоги: «Откуда взялось это число? Выдумывать числа нельзя! Что за чепуха!»
Чтобы облегчить душу, назовем новое число мнимым. В наших глазах такое число – второго сорта: мы не кладем i кубиков сахара в чашку кофе и не боимся, что расстояние до университета окажется равным i миль.
Мы просто решили поиграть и сами придумали правила. Хорошо, теперь давайте поразмышляем. Посмотрим, на что годно это число i. Мы знаем, что i × i = –1. А как насчет i + i? Если следовать привычным арифметическим правилам, то получится другое мнимое число: 2i. А что, если возвести это число в квадрат? Попробуем!
(2i) ² = (2i) × (2i) = 2 × i × 2 × i = 2 × 2 × i × i = 4 × (i × i) = 4 × (–1) = –4.
Другими словами, число 2i представляет собой квадратный корень из числа –4.
Теперь возведем в квадрат 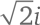 и посмотрим, что получится:
и посмотрим, что получится:
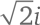 и посмотрим, что получится:
и посмотрим, что получится:
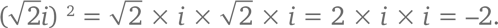
Таким образом, 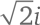 представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто
представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто  а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i, где b – это действительное число, называют мнимым числом.
а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i, где b – это действительное число, называют мнимым числом.
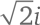 представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто
представляет собой квадратный корень из числа –2. Когда мы приютили мнимое число i в семье всех чисел, мы заполучили не просто  а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i, где b – это действительное число, называют мнимым числом.
а в придачу еще и квадратные корни из всех отрицательных действительных чисел! Любое число вида b × i, где b – это действительное число, называют мнимым числом.Если сложить два мнимых числа, например 2i и 4i, мы получим другое мнимое число: 6i. Если мы перемножим два мнимых числа, например 3i и –2i, то получим действительное число:
3i × (–2i) = 3 × (–2) × i × i = (–6) × (–1) = 6.
Комплексные числа
Чтобы мнимые числа прижились в семье всех чисел, нужно научиться складывать, вычитать, умножать и делить мнимые и действительные числа вместе. Мы будем работать с множеством комплексных чисел. Это расширение множества действительных чисел, включающее все числа вида a + bi, где a и b – действительные числа, например 3 + 4i.
Само число i комплексное, потому что может быть представлено в виде 0 + 1i. Точно так же действительные числа могут быть представлены в виде –7 + 0i.
Складывать комплексные числа несложно, мы просто приводим подобные слагаемые:
(3 + 2i) + (4 – 3i) = (3 + 4) + (2 – 3) i = 7 – i.
Более педантично мы можем записать это так: 7 + (–1) i.
Вычитание ничуть не сложнее:
(3 + 2i) – (4 – 3i) = (3 – 4) + (2 – (–3)) i = –1 + 5i.
Очевидно, что сумма или разность двух комплексных чисел – тоже комплексное число. На языке алгебры мы можем продублировать эту фразу так (числа a, b, c, d здесь – действительные):
(a + bi) + (c + di) = (a + c) + (b + d) i;(a + bi) – (c + di) = (a – c) + (b – d) i.
Умножение комплексных чисел дается несколько труднее. Попробуем перемножить наших друзей 3 + 2i и 4 – 3i:
(3 + 2i) × (4 – 3i) = 3 × (4 – 3i) + 2i × (4 – 3i) = (3 × 4 – 3 × 3i) + (2i × 4 – 2i × 3i) = (12 – 9i) + (8i + 6) = 18 – i.
На алгебраическом языке произведение двух комплексных чисел выражает формула:
(a + bi) × (c + di) = (ac – bd) + (ad + bc) i.
Очевидно, что при перемножении двух комплексных чисел мы получаем комплексное число.
Из всех арифметических операций деление комплексных чисел сложнее всего. Оно приводит нас к выражению (a + bi) / (c + di), поэтому сначала нам придется поговорить о взаимно обратных числах. Число x называют взаимно обратным числу y, если xy = 1. Например, дробь 1/2 взаимно обратна числу 2.
Какое комплексное число взаимно обратно 1 + 2i? Нам нужно такое число a + bi, что (1 + 2i) × (a + bi) = 1. Докажем, что этому требованию удовлетворяет число 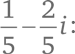
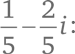

Общая формула для комплексного числа, обратного числу a + bi, выглядит следующим образом:

В этом легко убедиться: достаточно умножить (A) на a + bi, аккуратно произвести все необходимые арифметические действия – и получить в итоге единицу.
Заметим, что оба знаменателя в (A) равны a² + b². Если вдруг эта сумма окажется равной нулю, формула потеряет смысл, потому что деление на ноль запрещено. Но такое возможно лишь в том случае, если a = 0 и b = 0. Другими словами, все комплексные числа имеют взаимно обратные, кроме числа 0 + 0i. Это подтверждает ожидания: ноль – единственное действительное число, не имеющее взаимно обратного, и среди комплексных чисел дело обстоит так же. Но обратное по отношению к любому ненулевому комплексному числу – тоже комплексное число.
Расправившись со взаимно обратными числами, мы можем наконец перейти к делению. Деление числа X на число Y дает такой же результат, как умножение числа X на число, взаимно обратное Y. Следовательно, частное двух комплексных чисел (если делитель не равен нулю) – комплексное число.
Отсюда можно сделать вывод: основные арифметические действия – сложение, вычитание, умножение и деление – прекрасно справляются с комплексными числами. Мы можем проделать эти операции над парой любых комплексных чисел (исключение составляет деление на ноль) и получить комплексное число.
Сейчас мы снова попытаемся извлечь квадратный корень. Сперва именно эта задача загнала нас в тупик. Действительные числа, так сказать, неполноценны: из каких-то квадратный корень извлекается, а из каких-то – нет. И вот мы дополняем действительные числа мнимыми, придумав новое число  Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел. Но как решить вопрос с квадратным корнем? Чему равен
Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел. Но как решить вопрос с квадратным корнем? Чему равен 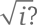 Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?
Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?
 Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел. Но как решить вопрос с квадратным корнем? Чему равен
Мы заново осваиваем арифметические операции, и система действительных чисел разрастается до системы комплексных чисел. Но как решить вопрос с квадратным корнем? Чему равен 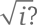 Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?
Нам что, опять нужно изобрести какое-то несуществующее число и создать монструозное множество «сверхкомплексных» чисел?К счастью, множество комплексных чисел уже содержит все квадратные корни из комплексных чисел. Посмотрим, как извлечь корень из мнимой единицы, не создавая новых сущностей.
Нам нужно найти такое комплексное число a + bi, что (a + bi) ² = i. Начнем с перемножения (a + bi) и (a + bi):
(a + bi) × (a + bi) = (a² – b²) + (2ab) i.
Теперь нам нужно приравнять это выражение к i = 0 + 1 × i. В результате мы получим: a² – b² = 0 и 2ab = 1.
Первое условие тождественно тому, что a = b или a = –b.
Если a = b и 2ab = 1, то 2a² = 1.
Таким образом, 

Так как a = b, мы нашли два квадратных корня из мнимой единицы:
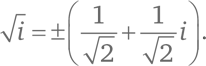
Проверьте, так ли это, возведя оба ответа в квадрат.
Если a = –b, решение будет таким же.
Итак, затратив некоторые усилия, мы показали, что извлечение квадратного корня из комплексного числа дает комплексное число, поэтому придумывать новые числа для извлечения корней не нужно.
Основная теорема алгебры
А как насчет кубических корней? Кубический корень из числа c – это такое число x, что x³ = c. Вопрос: входит ли множество корней из комплексных чисел во множество комплексных чисел или нам нужно изобретать еще какие-нибудь новые числа?
Уравнение x³ = c может быть записано иначе: x³ – c = 0. Сформулируем вопрос в общем виде: всякое ли полиномиальное уравнение имеет решение среди комплексных чисел? Скажем, есть ли такое комплексное число x, что
3x⁵ + (2 – i) x⁴ + (4 + i) x³ + x – 2i = 0?
Принципиально важный факт в теории комплексных чисел состоит в том, что любое полиномиальное уравнение имеет комплексное решение! Об этом говорит основная теорема алгебры. На математическом языке данный тезис можно переформулировать так: поле комплексных чисел алгебраически замкнуто.
Вот как звучит это важнейшее утверждение в строгой форме.
Теорема (основная теорема алгебры). Пусть d – положительное целое число и c0, c1, c2, …, cd – комплексные числа, причем cd ≠ 0. Тогда существует такое комплексное число z, чтоcdzd + cd – 1zd – 1 + … + c2z² + c1z + c0 = 0.
Поле действительных чисел незамкнуто, потому что среди действительных чисел не всегда можно найти решение полиномиального уравнения с действительными коэффициентами (например, среди действительных чисел нет такого числа a, что a × a + 1 = 0. Доказательство общей теоремы алгебры состоит в том, что решение приведенного выше полиномиального уравнение находят в общем виде.
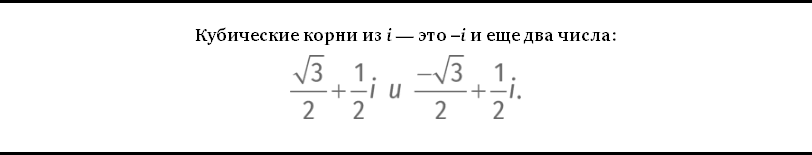
Назад: Глава 4 √2
Дальше: Глава 6 π

