Книга: Путеводитель для влюбленных в математику
Назад: Глава 12 Алгоритм
Дальше: Глава 14 Пифагор и ферма
Часть II
Геометрические фигуры
Глава 13
Треугольники
Треугольник – геометрическая фигура, состоящая из трех прямых отрезков, соединяющих три точки. В главе 13 мы рассмотрим общеизвестные свойства этих незамысловатых фигур и приподнимем покров над их тайнами. А начнем мы с двух всем знакомых формул: суммы углов и площади треугольника.
В сумме все это дает 180°
Возможно, самый известный факт, касающийся треугольников, – то обстоятельство, что если мы измерим все три угла и сложим эти величины, то получим 180°.
Почему мы так уверены? Нет, не стоит вырезать из бумаги тысячи треугольников и вымерять их углы транспортиром! Есть путь попроще.
Возьмем треугольник – любой треугольник – и обозначим его вершины буквами A, B, C, а величину углов соответственно x, y, z. Нам нужно убедиться, что x + y + z = 180°.
Нарисуйте (все равно, на бумаге или в воображении) прямую L, проходящую через точку B и параллельную AC:
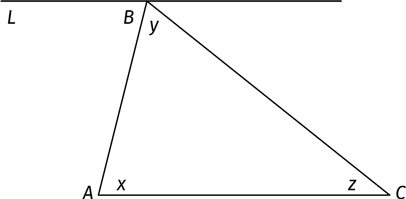
Продолжите отрезки AB и BC таким образом, чтобы они пересекали прямую L. В результате появятся три новых угла.
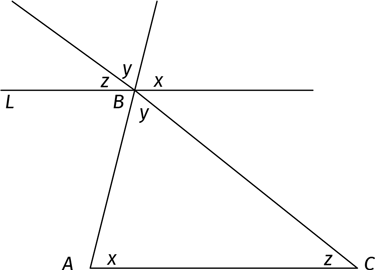
Обратите внимание, что они образуют развернутый угол и в сумме дают 180°.
На чертеже мы обозначили новые углы x, y, z, так как они в точности равны углам треугольника. Почему это происходит?
Когда две параллельные прямые пересекают третью, образуются два соответственных угла, которые равны друг другу. Кроме того, при пересечении двух прямых образуются два вертикальных угла, которые тоже равны друг другу. Это изображено на чертеже.
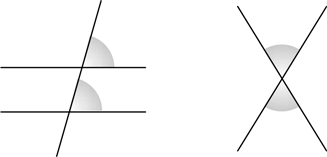
Взгляните на три новых угла x, y, z. Поскольку AC и L параллельны, прямая AB отсекает два равных соответственных угла – оба по x градусов. Точно так же прямая BC отсекает еще два равных соответственных угла – оба по z градусов. И, наконец, прямые AB и BC пересекаются в точке B и образуют два вертикальных угла – оба по y градусов.
Суммируем всё, что мы выяснили:
• Три новых угла охватывают ровно одну сторону линии L, поэтому их сумма – 180°.
• Три новых угла имеют ту же величину, что и три угла треугольника.
Поэтому мы заключаем, что x + y + z = 180°, как и было обещано.
Площадь
Бессчетное число школьников зазубривает: «Площадь треугольника равна половине произведения его основания на высоту». Напомню: основание – одна из сторон, а высота – кратчайшее расстояние от этой стороны до противолежащей вершины.
Если длина основания равна b, а высота – h, площадь треугольника можно вычислить по формуле:
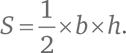
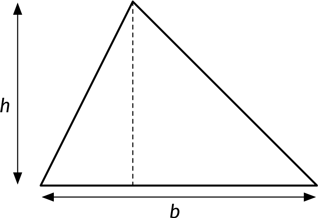
Общеизвестный факт! Но почему это так? Вот замечательное объяснение, и оно гораздо интереснее, чем формула.
Скопируем наш треугольник, поставим с ног на голову и прикрепим два треугольника друг к другу, чтобы получить параллелограмм:
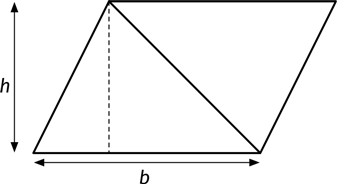
Его площадь будет вдвое больше площади нашего треугольника.
Теперь превратим параллелограмм в равный по площади прямоугольник: отрежем треугольник (он обозначен пунктирной линией) с одной стороны и прикрепим его с другой:
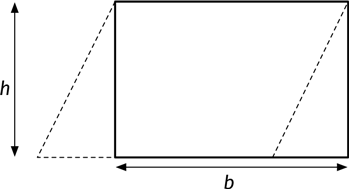
Получится прямоугольник со сторонами b и h, его площадь равна b × h. Таким образом, площадь нашего треугольника равна 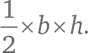
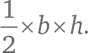
Если у нас есть материальный треугольник (скажем, деревянный), несложно измерить его стороны линейкой. Но измерить высоту не так-то просто. Мы прикладываем к вершине линейку, но должны быть уверены, что она перпендикулярна противоположной стороне.
Можно ли вычислить площадь треугольника, если мы знаем длины его сторон? Потребует ли это геркулесовых усилий? Здесь нам поможет герой по имени Герон – Герон Александрийский, живший около двух тысяч лет назад.
Обозначим длины сторон треугольника буквами a, b и c, как показано на рисунке.
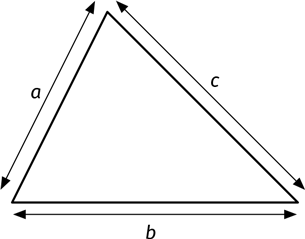
Вначале необходимо сложить эти числа и поделить пополам. Обозначим результат буквой s:
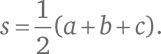
Теперь поочередно вычтем из получившейся величины длины сторон – и получим заветную формулу:

Например, длины сторон треугольника равны 4, 5 и 7. Тогда 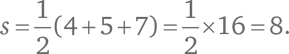 Это дает:
Это дает:
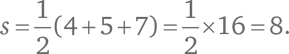 Это дает:
Это дает:

Вот развернутый вариант формулы Герона:
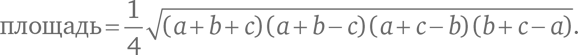
Перепроверим на только что разобранном примере:
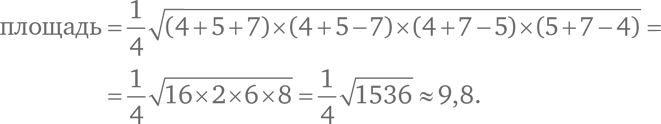
Есть и другие формулы вычисления площади треугольника. Я завершу этот раздел своей излюбленной формулой. Она работает для треугольника с целочисленными вершинами – их координаты на плоскости должны быть целыми числами. Это легко продемонстрировать на клетчатой бумаге:
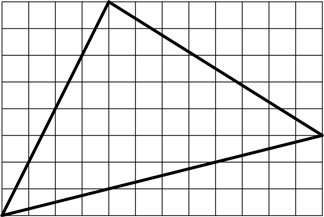
Будем считать, что площади всех квадратиков равны 1. Можно найти площадь треугольника, посчитав, сколько квадратиков укладывается внутри треугольника целиком, а затем прибавив площади фрагментов квадратиков, отсеченных сторонами треугольника. Однако нам придется нелегко.
Теорема Пика предлагает кое-что полегче. Мы не будем считать квадратики – мы посчитаем координатные точки. Вначале найдем, сколько точек внутри треугольника; обозначим их число I. Затем посчитаем количество точек на границе треугольника; обозначим их число B.
Теорема Пика утверждает:
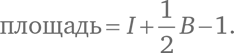
Я начертил достаточно крупный треугольник, чтобы вы смогли сосчитать все точки. В итоге получится, что I = 38, а B = 10 (включая вершины). Таким образом,
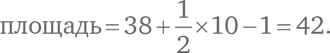
Завершу этот раздел небольшой головоломкой. Предположим, мы хотим найти площадь четырехугольника с целочисленными вершинами. Если внутри четырехугольника I координатных точек, а на границе B координатных точек (включая четыре вершины), то чему равна его площадь? Ответ вы найдете в конце главы.
Кроме того, подумайте над вопросом о площади других многоугольников с целочисленными вершинами: пятиугольнике, шестиугольнике и т. д.
Центры
Что мы подразумеваем, когда говорим «центр треугольника»? У этого понятия есть несколько значений, и каждое интересно по-своему.
Начнем с точки под названием центроид треугольника. Соединим вершины треугольника с серединами противоположных сторон. Такие отрезки называют медианами. Удивительно: все три медианы пересекаются в одной точке; ее и называют центроидом.
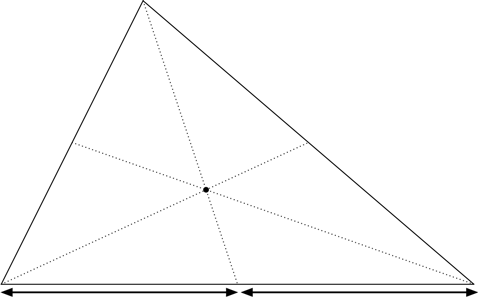
Одно из свойств центроида – он представляет собой центр масс треугольника: если треугольник из жесткого материала (скажем, из тонкого листа железа) подвесить за центр масс, он будет сохранять равновесие. Разумеется, равновесие окажется шатким, если наши вычисления окажутся недостаточно точными.
Мы уже провели отрезки из вершин треугольника к серединам противолежащих сторон; теперь давайте проведем кратчайшие линии, соединяющие вершины и противолежащие стороны. Они будут пересекать стороны треугольника под прямыми углами. Ко всеобщему восхищению эти три отрезка также пересекаются в одной точке; ее называют ортоцентр.
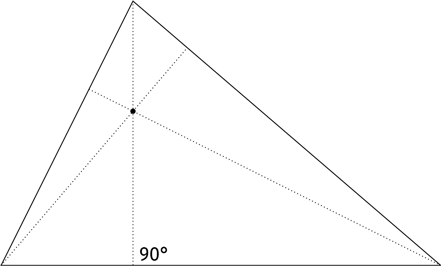
Далее: биссектрисы. Проведем три отрезка из трех вершин до трех противоположных сторон, чтобы каждый из них рассекал соответствующий угол треугольника на два равных между собой угла. Эти три отрезка вновь пересекаются в одной точке, известной как инцентр.
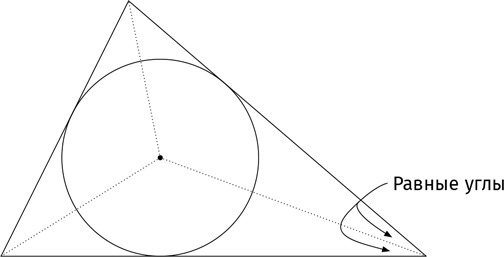
Инцентр называют так потому, что это центр окружности, касающейся всех трех сторон треугольника (вписанной в треугольник окружности).
Теперь проведем отрезки не из вершин треугольника, а из середин его сторон, причем под прямыми углами к этим сторонам; их называют серединные перпендикуляры. Имею счастье сообщить, что и они пересекаются в одной точке – в центре окружности, описанной около треугольника, то есть содержащей все три его вершины.
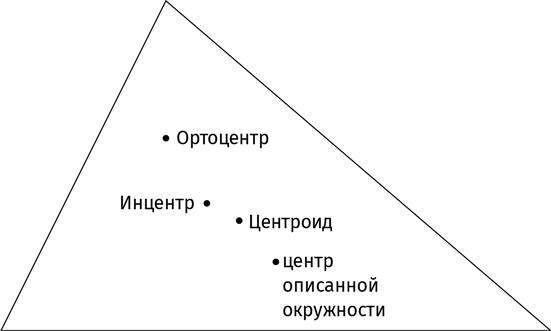
Эти четыре центра (центроид, ортоцентр, инцентр и центр описанной окружности) совпадают, если треугольник равносторонний. Но в общем случае точки различаются. На рисунке вы можете видеть расположение всех четырех центров в некотором произвольном треугольнике.
Охота на равносторонние треугольники
Вместо биссектрис проведем трисектрисы углов треугольника – отрезки, рассекающие каждый угол треугольника на три равные между собой части. В общей сложности это будет шесть отрезков (по два для каждого угла). Разумеется, все они не могут пересечься в одной точке, но точки, где они пересекаются, образуют малый треугольник внутри большого.
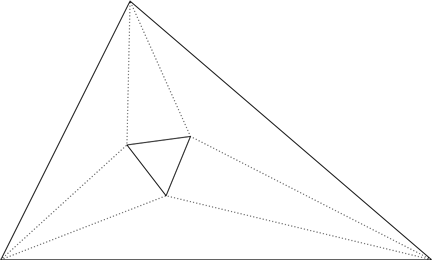
Ошеломительная теорема Морли утверждает, что этот малый треугольник всегда будет равносторонним!
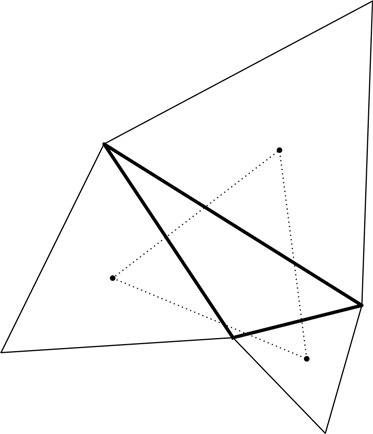
Можно отыскать и другой равносторонний треугольник, сопутствующий любому произвольно взятому треугольнику. Построим на трех сторонах треугольника (на рисунке он начерчен жирными линиями) три равносторонних треугольника (начерчены тонкими линиями). Отметим центры этих равносторонних треугольников:
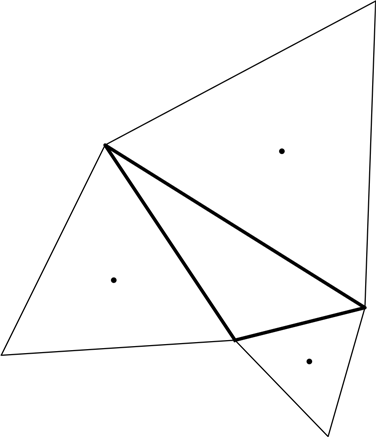
Соединим три центра и – вуаля! – получим очередной равносторонний треугольник.
Теорема Пика для четырехугольников
Нарисуем четырехугольник с целочисленными вершинами на клетчатой бумаге и проведите диагональ. Таким образом, мы получаем два треугольника с общей стороной:
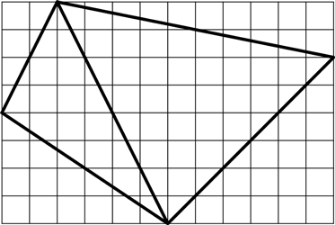
Мы можем посчитать площади двух треугольников, пользуясь теоремой Пика, а затем сложить получившиеся величины. Обозначим эти два треугольника L и R и получим:

Таким образом, площадь четырехугольника равна 16 + 36 = 52.Но, ко всеобщему восхищению, теорема Пика верна также для четырехугольников! И вот почему.Вместо нового пересчета точек давайте воспользуемся результатами, уже полученными ранее.Внутри левого треугольника 13 точек, внутри правого – 31 точка. Обратите внимание, что три точки на диагонали тоже лежат внутри четырехугольника; включим их в наши расчеты. Это дает IQ= 31 + 13 + 3 = 47.Что касается границ четырехугольника, мы видим 8 точек на границе левого треугольника и еще 12 – на границе правого, то есть в общей сложности 20 точек. Но тут мы немного перебрали. Три точки на диагонали четырехугольника включать не надо; кроме того, мы посчитали их дважды. Таким образом, нужно вычесть 6. Две точки на концах диагонали тоже посчитаны дважды, потому вычтем еще 2, чтобы компенсировать перебор. Это дает BQ= 20–6–2 = 12.Последний рывок:
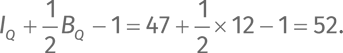
Невероятно! Это правильный ответ! Как такое возможно?Площади двух треугольников, L и R, дают в сумме:
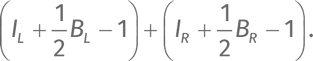
Это не что иное, как площадь четырехугольника. Перегруппируем слагаемые:
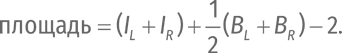
Величина IL + IR не включает некоторые точки внутри четырехугольника, а величина BL + BR оказывается слишком большой из-за точек на границах. Точки на диагонали четырехугольника мы неосмотрительно посчитали дважды, хотя на самом деле они принадлежат величине IQ (и деление пополам исправляет эту оплошность). Конечные точки диагонали тоже оказались посчитаны дважды, когда мы вычисляли точки на границах. Деление на 2 исправляет эту оплошность лишь наполовину, но вычитание 2 (а не 1) ставит все на свои места!Вы не поверите, но теорема Пика работает для любого многоугольника с целочисленными вершинами.Центры треугольника вне треугольника
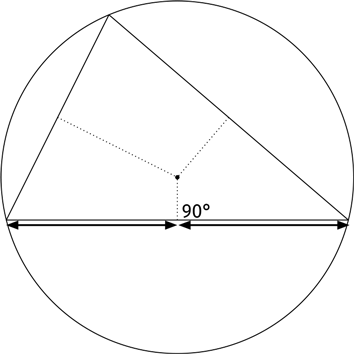
Если треугольник тупоугольный (то есть один из его углов больше 90°), центр описанной окружности и ортоцентр лежат вне треугольника. На рисунке приведен пример окружности, описанной около тупоугольного треугольника.
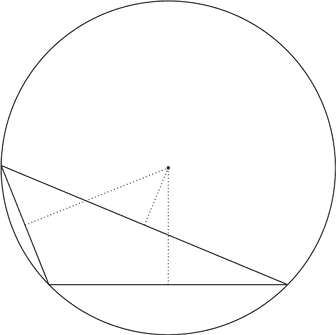
Найти ортоцентр тупоугольного треугольника несколько сложнее. Фокус состоит в том, чтобы продолжить его стороны, пока они не пересекутся с соответствующими высотами.
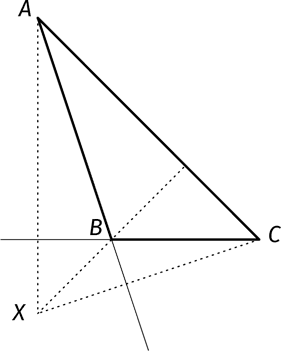
В треугольнике ABC мы делаем следующие дополнительные построения: (1) проводим через точку A прямую, перпендикулярную BC (эту сторону необходимо продолжить); (2) проводим через точку B прямую, перпендикулярную AC; (3) проводим через точку С прямую, перпендикулярную AB (ее также необходимо продолжить). Точка пересечения этих прямых X и есть ортоцентр.
Назад: Глава 12 Алгоритм
Дальше: Глава 14 Пифагор и ферма

