Книга: Магия математики: Как найти x и зачем это нужно
Назад: Мнимое число i: квадратный корень –1
Дальше: Магия числа e
Геометрия комплексных чисел
Комплексные числа можно представить в виде комплексной же плоскости. Выглядит она так же, как и алгебраическая система координат (x, y), только вместо оси y мы чертим некую мнимую ось, на которой расположены числа 0, ±i, ±2i и так далее. Вот как будут выглядеть на этой плоскости некоторые комплексные величины:
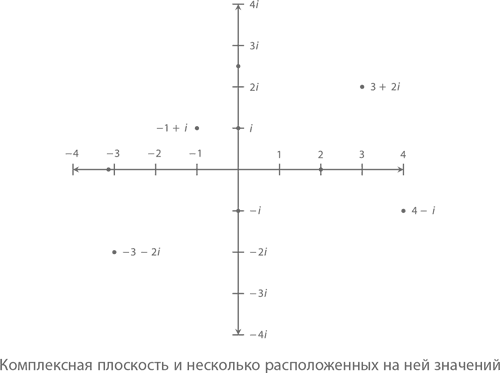
Только что мы выяснили, насколько легко складывать, вычитать и умножать числовые выражения комплексных величин. С их геометрическими представлениями работать ничуть не сложнее: достаточно просто взглянуть на соответствующие точки.
Возьмем, к примеру, сложение:
(3 – 2i) + (–1 + i) = 2 + 3i
Посмотрите на график ниже: точки 0, 3 + 2i, 2 + 3i и –1 + i образуют параллелограмм.
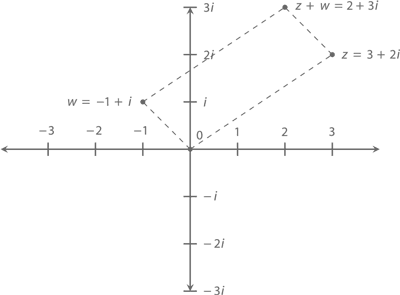
Вы удивитесь, но его вполне достаточно, чтобы сложить комплексные числа z и w.
Для вычитания z – w возьмем третью точку – w, расположенную симметрично напротив w. А теперь просто сложим z и – w, как показано на графике:
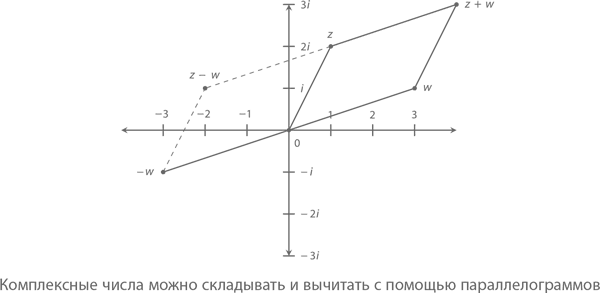
Для умножения и деления нам понадобится измерить комплексные величины. Модулем (или длиной) любого комплексного числа считается длина отрезка от начала координат 0 до точки, соответствующей искомому числу. То есть модуль числа z (обозначается как |z|) есть расстояние от 0 до точки z. Если z = a + bi, тогда, согласно теореме Пифагора, модуль z будет равен
|z| = √(a² + b²)
На графике ниже хорошо видно, что точка 3 + 2i имеет модуль √(3² + 2²) = √13. Обратите внимание, что для соответствующего этой точке угла θ tan θ = 2/3. Следовательно, θ = tan–12/3 ≈ 33,7° или примерно 0,588 рад.
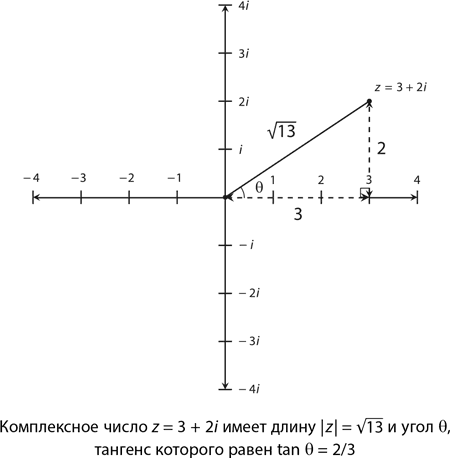
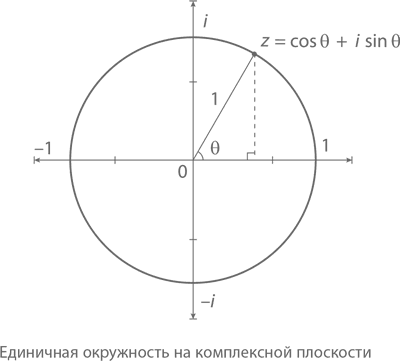
Точки с модулем, равным 1, складываются в единичную окружность (см. график ниже). Чему будет равно комплексное число, образующее угол θ? Если бы мы находились в более привычной системе координат, нужная нам точка имела бы координаты (cos θ, sin θ) – это нам хорошо известно по предыдущей главе. Значит, здесь получаем cos θ + i sin θ. То есть любая комплексная величина с модулем R соответствует формуле
z = R(cos θ + i sin θ)
что есть не что иное, как тригонометрическое представление этого числа. Забегу немного вперед: в конце главы мы выясним, что равно оно будет Reiθ.
А вот еще кое-что интересное: при перемножении комплексных чисел будут перемножаться и их модули.
Теорема: Для комплексных величин z1 и z2 |z1z2| = |z1| |z2|. Иными словами, модуль произведения есть произведение модулей.

Например,
|(3 + 2i)(1 – 3i)| = |9 – 7i| = √(9² + (–7)²)√130 = √13√10 = |3 + 2i| |1 – 3i|
А что насчет угла, привязанного к произведению? Для обозначения угла, образованного комплексным z и «положительной» половиной оси x, обычно используется представление arg z. Так, arg (3 + 2i) = 0,588 рад. Аналогично arg (1 – 3i) = tan–1 (–3) = –71,56° = –1,249 рад, потому что значение 1 – 3i располагается в квадранте IV, а тангенс его угла θ равен –3.
Обратите внимание, что угол значений (3 + 2i)(1 – 3i) = (9 – 7i) имеет tan–1 (–7/9) = –37.87° = –0,661 рад, что есть 0,588 + (–1,249). И имеется теорема, которая доказывает, что это совсем не совпадение!
Теорема: Для комплексных величин z1 и z2 arg (z1z2) = arg (z1) + arg (z2). Другими словами, угол произведения есть сумма углов.
Доказательство этого (оно приведено в «отступлении») основано на некоторых тригонометрических тождествах, рассмотренных нами в предыдущей главе.
Отступление
Доказательство: Возьмем две комплексные величины z1 и z2, имеющие модули R1 и R2 и углы θ1 и θ2 соответственно. Записав их в тригонометрическом представлении, имеемz1 = R1 (cos θ1 + i sin θ1)
z2 = R2 (cos θ2 + i sin θ2)
Тогда на основании тождеств cos (A + B) и sin (A + B)z1 z2 = R1(cos θ1 + i sin θ1) R2(cos θ2 + i sin θ2) = R1 R2 [cos θ1 cos θ2 – sin θ1 sin θ2 + i(sin θ1 cos θ2 + sin θ2 cos θ1)] = R1 R2 [cos(θ1 + θ2) + i(sin(θ1 + θ2))]
Следовательно, z1z2 имеет модуль R1R2 (что нам уже известно) и угол θ1 + θ2, что и требовалось доказать.◻
Обобщим: чтобы умножить комплексные величины, нужно умножить их модули и сложить их углы. К примеру, при умножении некоего числа на i модуль останется прежним, а угол «вырастет» на 90°. Имейте в виду, что при перемножении двух действительных величин положительные числа будут иметь углы, равные 0° (или, что то же самое, 360°), а отрицательные – 180°. Два угла по 180° дадут в сумме 360° – еще одно доказательство, что произведение двух отрицательных величин есть величина положительная. Мнимые же числа имеют углы, равные либо 90°, либо –90° (или 270°). Следовательно, при умножении такого числа на само себя угол должен быть равен 180° (так как 90° + 90° = 180°, а –90° + –90° = –180°, что ничем не отличается от 180°), что соответствует отрицательной величине.
Ну и, наконец, возьмем число z с углом θ: 1/z должно иметь угол –θ. (Почему? Да потому что z · 1/z = 1, то есть z и 1/z должны в сумме давать 0°.)
Получается, что при делении комплексных чисел, мы делим их модули и вычитаем их углы: z1/z2 имеет модуль R1/R2 и угол θ1 – θ2.

Назад: Мнимое число i: квадратный корень –1
Дальше: Магия числа e

