Магия числа e

Книга: Магия математики: Как найти x и зачем это нужно

Если вдруг у вас под рукой есть профессиональный калькулятор, сделайте вот что:

1. Наберите на нем любое хорошо запоминающееся семизначное число (можно взять номер телефона, несколько цифр из номера паспорта или просто любимую цифру, повторенную семь раз).

2. Посчитайте обратную ему величину (для этого нужно нажать кнопку 1/x).

3. Прибавьте к нему единицу.

4. Возведите результат в степень, равную загаданному семизначному числу (нажимаете кнопку x^y, вводите семь цифр и нажимаете «равно»).

Первые четыре цифры ответа – 2,718, да? Не удивлюсь даже, если у вас получится

e = 2,718281828459045…

то есть цифр, совпадающих с иррациональным числом e, будет куда больше.

Так что это за мистическое e такое, в чем его секрет и зачем оно вообще нужно?

Ваши операции с калькулятором свелись, по сути, к

(1 + 1/n)ⁿ

где n и есть ваше семизначное число. Семь знаков – много, но что будет, если их будет еще больше? С одной стороны, число (1 + 1/n) будет все ближе и ближе подбираться к единице, которая при возведении в степень останется единицей. Следовательно, было бы разумным предположить, что при любом большом значении n (1 + 1/n)ⁿ будет приблизительно равно единице (например, 1,001¹⁰⁰ ≈ 1,105).

С другой стороны, даже при больших значениях n результат (1 + 1/n) никогда не опустится ниже этой самой единицы. А при последовательном возведении такого числа во все бо́льшую и бо́льшую степень, увеличиваться будет и итог (скажем, 1,001^{10 000} будет больше 20 000).

Сложность здесь заключается в том, что «основа» (1 + 1/n) становится тем меньше, чем больше возрастает n. И это постоянное «перетягивание каната» между единицей и бесконечностью пододвигает ответ все ближе и ближе к e = 2,71828… (Так, 1,001¹⁰⁰⁰ ≈ 2,717.)

Давайте посмотрим повнимательнее, как ведет себя функция (1 + 1/n)ⁿ при возрастающих значениях n:

Именно так и определяется число e: как величина, к которой приближается (1 + 1/n)ⁿ с возрастанием значения n. Математики называют ее пределом (1 + 1/n)ⁿ при n, стремящейся к бесконечности. Записывается это следующим образом:

Если заменить дробь 1/n на x/n, оговорившись, что x есть действительная величина, то с возрастанием n/x число (1 + x/n)^n/x будет все больше приближаться к e. Возведя обе части этого уравнения в степень x (и вспомнив, что (a^b)^c = a^bc), мы приходим к экспоненциальной формуле:

где х – любое комплексное число. Вы удивитесь, но от этой формулы есть вполне себе практическая польза. Предположим, что вы открыли в банке накопительный счет под 6 % годовых (то есть ставка составит 0,06) и положили на него $10 000. Если процент начисляется раз в год, то через 365 дней у вас будет $10 000(1,06) = $10 600. Именно от этой суммы банк будет исчислять 6 % в следующем году: $10 000(1,06)² = $11 236. Через три года уравнение преобразуется в $10 000(1,06)³ = $11 910,16. Через t же лет – в

$10 000(1,06)^t

Чтобы отследить общую закономерность, заменим ставку 0,06 ставкой r, а начальную сумму $10 000 суммой $P. Тогда через t лет вы смогли бы получить

$P(1 + r)^t

Теперь предположим, что проценты начисляются дважды в год: по 3 % каждые 6 месяцев. Через год на вашем счете будет лежать $10 000(1,03)² = $10 609 – немного больше, чем в прошлом случае.

С ежеквартальными (раз в три месяца) начислениями вы заработаете 4 раза по 1,5 %, то есть $10 000(1,015)⁴ = $10 613,63.

Давайте обобщим и это: при начислении процента n раз в год через 365 дней сумма ваших накоплений составит

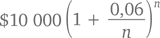
При очень больших значениях n мы будем иметь дело с непрерывными начислениями процента. Согласно второму замечательному пределу, за год получится

Сведем все это в таблицу:

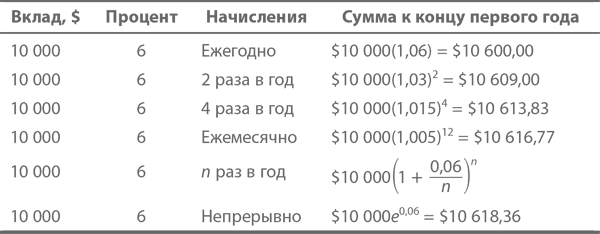
Иными словами, начав с $P, с непрерывными начислениями по ставке r через t лет вы получите $A. Все это выражается очень симпатичной во всех отношениях формулой

A = Pe^rt

Как хорошо видно на графике, функция y = e^x растет очень быстро. По соседству с ней мы изобразим графики e^2x и e^0,06x. Правда, похожи? Подобный рост называется ростом по экспоненте. Если же взять график y = e^–x, то он очень быстро приближается к 0, то есть демонстрирует спад по экспоненте.

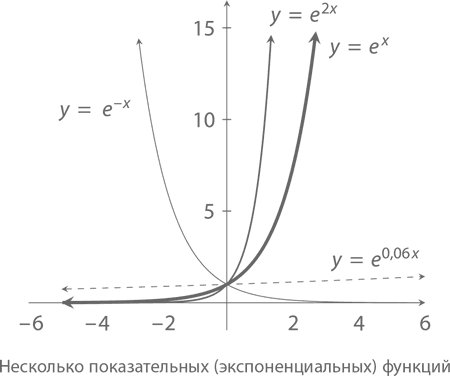
А что насчет графика 5x? Так как e < 5 < e², он должен лежать между e^x и e^2x. Если точнее, то e^1,609… = 5, следовательно, 5^x ≈ e^1,609x. В целом же любую функцию a^x можно представить в виде e^kx, где k есть экспонента, соответствующая a = e^k. А для того, чтобы найти k, нам понадобятся логарифмы.

Точно так же, как квадратный корень является обратным представлением квадратичной функции (то есть находится с ней во «взаимоотменяющих» отношениях), логарифм является обратным представлением показательной (экспоненциальной) функции. Наиболее часто используемый логарифм – десятичный (то есть по основанию 10), обозначаемый как lg x. Считается, что

y = lg x если 10^y = x

из чего следует

10^lg^x = x

Например, так как 10² = 100, lg 100 будет равен 2. Вот очень полезная таблица логарифмов:

Одной из причин популярности логарифмов является их уникальная способность преобразовывать огромные значения в малые, куда более удобоваримые для человеческого ума. Логарифмы, в частности, используются при измерении и подсчете магнитуды землетрясения по шкале от 1 до 10 (да-да, это я о знаменитой шкале Рихтера), громкости звука (в децибелах), кислотности химических растворов (pH) и даже рейтинга посещаемости интернет-страниц (в алгоритме PageRank, придуманном корпорацией Google).

Что собой представляет lg 512? Любой профессиональный калькулятор (равно как и большинство поисковых систем в Интернете) скажет вам, что log 512 = 2,709…. Вполне похоже на правду: 512 находится между 10² и 10³, а значит, его логарифм должен быть больше 2, но меньше 3.

Логарифмы были изобретены для того, чтобы преобразовывать умножение в более простое сложение. Основано это на одной любопытной теореме.

Теорема: Для любых положительных значений x и y

log xy = log x + log y

Другими словами, логарифм произведения равен сумме логарифмов.

Доказательство: Согласно правилам действий со степенями,

10^lg^{x + lg y} = 10^lg^x 10^lg^y = xy = 10^lg^xy

Следовательно, возведение 10 в степень lg x + lg y дает xy, что и требовалось доказать.◻

Не менее полезно следующее правило.

Теорема: Для любого положительного значения x и любого целого значения n

log xⁿ = n log x

Доказательство: Согласно правилам действий со степенями, a^bc = (a^b)^c. Следовательно,

10^{n lg x} = (10^lg^x)ⁿ = xⁿ

то есть логарифм xⁿ равен n lg x.◻

Десятичный логарифм – штука вполне себе обычная, насколько вообще обычным может быть нечто столь активно использующееся в таких важных областях науки, как химия, физика или геология (справедливости ради все же следует упомянуть, что в информатике и дискретной математике предпочтение отдается логарифму с основанием 2). В целом же для любого значения b > 0 логарифм по основанию b log_b определяется согласно следующему правилу

y = log_b x если b^y = x

Так, log₂ 32 = 5, потому что 2⁵ = 32. А все уже рассмотренные нами свойства логарифмов соответствуют любому значению b. Так, например,

b^{logb x} = x
log_b xy = log_b x + log_b y
log_b xⁿ = n log_b x

В большинстве разделов математики, физики и техники самым полезным считается логарифм по основанию b = e. Он называется натуральным и даже имеет свое специальное обозначение – ln x. То есть

y = ln x если e^y = x

Или же, для всех действительных значений x,

ln e^x = x

Ваш калькулятор, например, может за долю секунды подсчитать, что ln 5 = 1,609…, однако это нам уже хорошо известно по тому, что e^1,609 ≈ 5. Подробнее же о функциях натурального логарифма мы поговорим в главе 11.

Отступление
Большинство профессиональных калькуляторов способно считать как натуральные, так и десятичные логарифмы. И лишь очень немногие ориентированы на другие значения b. Впрочем, проблемы тут никакой нет: одно основание довольно легко преобразовать в другое. Да-да, один логарифм является ключом ко всем остальным! На этот счет даже есть своя теорема, благодаря которой мы можем, например, взять логарифм по основанию 10 и найти его аналог по основанию b.

Теорема: Для любых положительных значений b и x

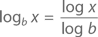
Доказательство: Предположим, что y = log_b x. Тогда b^y = x. Прологарифмируем обе части: log b^y = log x. Согласно второму замечательному пределу, y log b = log x. Следовательно, y = (log x)/(log b), что и требовалось доказать.◻

ln x = (log x) / (log e) = (log x) / (0,434…) ≈ 2,30 log x
logb x = (log x) / (log 2) = (log x) / (0,301…) ≈ 3,32 log x

Назад: Геометрия комплексных чисел

Дальше: Другие лики е