Загадочная природа числа i кроется в формуле

На первый взгляд это кажется совершенно невозможным: разве может быть отрицательным число, умноженное несколько раз на само себя? В конце концов, даже 0² = 0, а любая возведенная в квадрат отрицательная величина обязана стать положительной, разве нет? Не спешите рубить с плеча. Вспомните, ведь было такое время, когда вы вообще ничего не знали об отрицательных числах, да и, узнав, вряд ли сразу же поверили в их существование (как и многие-многие математики до вас). Что это вообще за глупость – количество, меньшее, чем 0? Как что-то может быть меньше, чем ничто? Но потом в вашей жизни появляется некая ось (вроде той, что изображена чуть ниже), а вместе с ней – и все ее обитатели: положительные значения, расположившиеся справа от 0, и отрицательные значения, расположившиеся слева. В точно таком же, нестандартном ключе нам следует рассматривать и число i – тогда-то нам и откроется его истинное, реальное значение.

Число i считается мнимым – таким, которое при возведении в квадрат дает отрицательный результат. Мнимое число 2i, например, дает (2i)(2i) = 4i² = –4.

В алгебраическом смысле мнимые числа ничем не отличаются от чисел действительных. Судите сами:

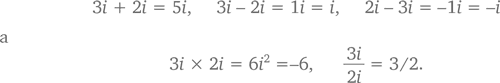
Кстати, если взять и возвести в квадрат – i, получится тот же результат (–1), потому что (–i)(–i) = i² = –1. Не менее предсказуемы и последствия перемножения мнимого и действительного чисел – скажем, 3 × 2i = 6i.

А что со сложением? Чему, например, равна сумма 3 и 4i? Очевидно, что 3 + 4i, и дальше с этим ничего сделать нельзя (равно как и ничего нельзя сделать с 1 +√3). Числа, образованные по модели a + bi (где a и b суть действительные величины), называются комплексными. Получается, что любая величина, будь она действительной (при b = 0) или мнимой (при a = 0), есть, по своей сути, особая форма комплексного числа. То есть действительное π и мнимое 7i будут также комплексными.

Давайте попробуем разобраться в этом с помощью нескольких конкретных примеров. Начнем со сложения и вычитания:

Для умножения применим алгебраический метод FOIL, описанный в главе 2:

Для комплексного числа каждый квадратный многочлен ax² + bx + c будет иметь два корня (или же один, но повторяющийся). Согласно формуле корней квадратного уравнения, многочлен будет равен 0 всякий раз, когда

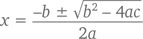
Помните, в главе 2 мы с вами говорили о том, что нельзя извлечь квадратный корень из отрицательной величины? Но ведь никакие квадратные корни отрицательных величин нам и не нужны. Смотрите сами: уравнение x² + 2x + 5, например, имеет корни

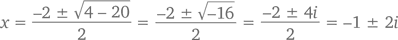
Кстати, формула корней квадратного уравнения будет верна даже при комплексных значениях a, b или c.

В любом квадратном многочлене мы можем найти как минимум один корень, пусть и комплексный. На этот счет есть своя теорема.

Теорема (основная теорема алгебры): Любой многочлен p(x), возводимый в первую или бо́льшую степень, имеет корень z при p(z) = 0.

Обратите внимание, что многочлен первой степени, вроде 3x – 6, может быть представлен как 3(x – 2), где 2 есть единственный корень 3x – 6. Обобщая, можно сказать, что при a ≠ 0 многочлен ax – b можно представить в виде a(x – (b/a)), где b/a будет являться корнем ax – b.

То же происходит и с многочленами второй степени: разложив ax² + bx + c до a(x – z₁)(x – z₂), мы получаем его корни – z₁ и z₂ (они вполне могут оказаться комплексными величинами, равно как и одной и той же величиной). И так можно продолжать до бесконечности – с любым многочленом любой степени.

Сопутствующая теорема: Любой многочлен степени n ≥ 1 может быть разложен на n составляющих. А именно: если p(x) есть многочлен n-ной степени, в котором главный член a ≠ 0, должно существовать n чисел z₁, z₂…., zn (которые вполне могут оказаться комплексными величинами, равно как и одной и той же величиной), соответствующих p(x) = a(x – z₁)(x – z₂)… (x – z_n). Величины zi являются корнями многочлена при p(z_i) = 0.

Теорема эта означает, что любой многочлен степени n ≥ 1 будет иметь как минимум один и как максимум n различных корней.

Например, x⁴ – 16 есть многочлен четвертой степени. Следовательно, его можно разложить как

из чего очень хорошо видно, что у него будет четыре различных корня: 2, –2, 2i, – 2i.

А вот многочлен третьей степени 3x³ +9x² –12 раскладывается так:

то есть имеет только два различных корня: –2 и 1.