До сих пор нам встречались углы, значения которых находились исключительно в диапазоне от 0 до 360 градусов. Но пристальный взгляд на единичную окружность невольно заставляет усомниться в обоснованности выбора числа 360. Сделан он был давным-давно, еще в древнем Вавилоне, где в обиходе была шестидесятеричная система счисления, использовавшаяся в том числе и в календаре (да-да, число 360 подозрительно напоминает количество дней в году). Альтернатива была предложена много позже, в XIX веке, когда в математике – а затем и в других науках – появилось понятие радиана, представляющего собой

или, другими словами,

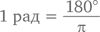
Для тауистов, почитающих число t как 2π,

В числовом же выражении 1 радиан примерно равен 57°.

Но зачем они нужны, спросите вы. И чем вдруг научному сообществу так не угодили привычные всем градусы?

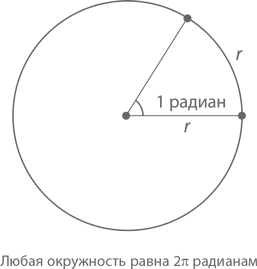
В круге с радиусом r угол в 2π радианов охватывает длину окружности 2πr. Если взять часть этого большого угла, величина дуги, отделяемой этой частью, будет в 2πr раз больше получившейся дроби. Если говорить конкретнее, то 1 радиан «захватывает» дугу длиной 2πr(1/2π) = r, а m радианов – дугу длиной mr. В единичной окружности значение угла в радианах равно длине соответствующей ему дуги. Разве не удобно?

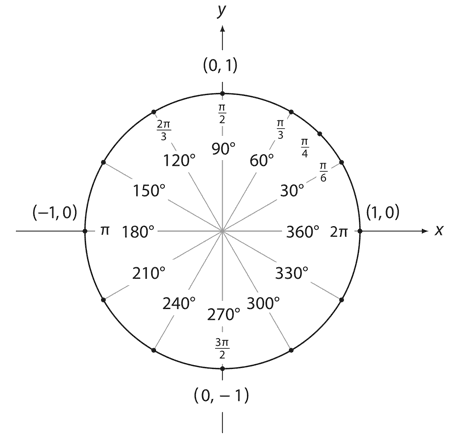
А вот единичный круг, поделенный на самые «популярные» углы – значения выражены как в градусах, так и в радианах.

Для сравнения – версия с t вместо π.

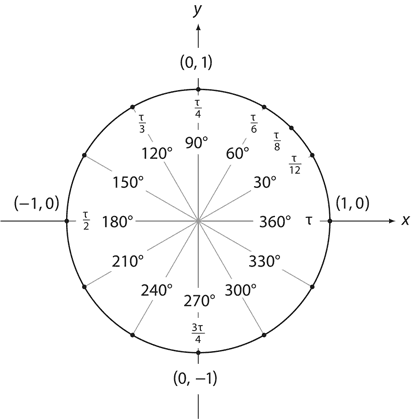
На рисунках, кстати, очень хорошо заметно, насколько t удобнее π. Для угла 90° (занимающего четверть окружности) представление в радианах выглядит как t/4; для угла 120° (треть окружности) – как t/3; для угла 60° (одна шестая окружности) – как t/6; t же есть, по сути, один полный оборот, то есть угол 360°.

Как нам еще предстоит убедиться, радианы позволяют значительно упростить формулы и уравнения подсчета тригонометрических функций. Формулы синуса и косинуса, например, можно превратить в «бесконечные ряды многочленов»:

но только если x измеряется в радианах. Или при исчислении, например, мы увидим, что cos x есть производная функция sin x при том же условии. Так же и графики тригонометрических функций y = sin x и y = cos x строятся обычно на основании радианного представления x.

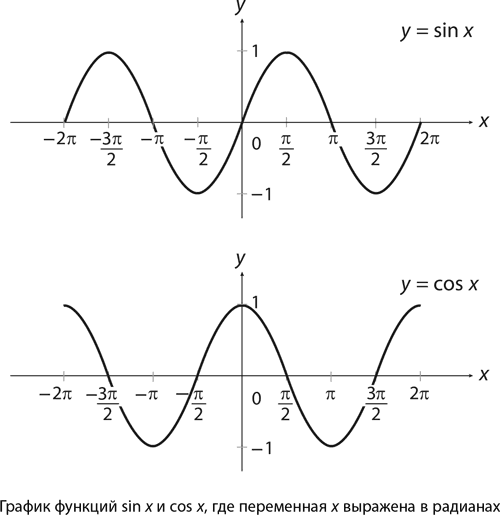
Графики эти будут повторяться с шагом 2π (тауисты, на старт!). Происходит это из-за того, что как синус, так и косинус берут свои начала в окружности, а угол x + 2π по своей природе ничем не отличается от угла x. Именно поэтому эти функции называются периодическими, а шаг 2π – периодом синуса и косинуса. Кстати, если сдвинуть график косинуса вправо на π/2, он точь-в-точь совпадет с графиком синуса, потому что значение π/2 в радианах соответствует углу 90°. Из всего этого следует, что

(например, sin 0 = 0 = cos (–π/2), а sin π/2 = 1 = cos 0).

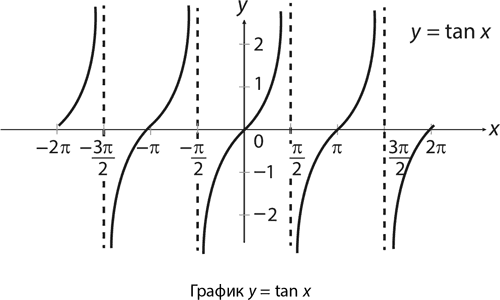
Тангенс, равный, как мы помним, sin x/cos x, так и останется неопределенным при cos x = 0 (что происходит всякий раз, когда линия графика проходит ровно посередине двух значений, кратных числу π). Значит, период тангенса равен π.

Синуса и косинуса, в принципе, достаточно, чтобы прийти к любой другой периодической тригонометрической функции. Именно благодаря такому своему уникальному свойству, как периодичность, они обрели огромную популярность для решения практических задач, в условиях которых заложена цикличность и «сезонность». Это и измерение температур, и анализ экономических данных, и многое другое. А еще с тригонометрическими функциями так или иначе связаны звуковые колебания, волны на воде, электричество и даже сердцебиение.

Ну и, по традиции, в завершение главы – самое интересное: между тригонометрией и числом π существует удивительная, поистине волшебная связь. Хотите ее увидеть? Возьмите калькулятор и наберите на нем столько пятерок, сколько получится. У меня, например, на экране уместилось их целых 16 – 5 555 555 555 555 555. Теперь посчитайте величину, обратную этому числу; у меня получилось

Нажмите кнопку «sin» и посмотрите, что у вас получилось (вначале может идти несколько нолей – просто не обращайте на них внимания). Лично на меня с дисплея смотрело число

которое (после отбрасывания 17 нолей, идущих за запятой) почти в точности повторяло первые 16 цифр числа π! К тому же результату можно прийти, начав с любого числа, состоящего как минимум из пяти пятерок.

В этой главе мы выяснили, зачем нужна тригонометрия, и увидели, как она помогает нам лучше понять свойства треугольников и окружностей. Тригонометрические функции – не просто «вещи в себе», они взаимодействуют, вступая друг с другом в замысловатые, но прекрасные в своей стройности отношения. А еще мы проследили их связь с числом π. Теперь черед за двумя другими важнейшими для математики величинами: иррациональной e = 2,71828… и мнимой i.