Тригонометрические тождества

Книга: Магия математики: Как найти x и зачем это нужно

Дальше: Радианы и графики в тригонометрии

Но этим возможности тригонометрических функций не ограничиваются. Они способны и на куда более интересные и запутанные взаимоотношения – так называемые тождества. Некоторые из таких тождеств мы уже наблюдали, например,

sin (–A) = –sin A
cos (–A) = cos A

Но их, конечно же, куда больше.

Из тождеств рождаются формулы, притом весьма полезные. Ими-то мы и займемся в этом разделе.

Первое тождество основывается на формуле единичной окружности:

x² + y² = 1

Под эту формулу должна подходить точка (cos A, sin A), принадлежащая единичной окружности. Следовательно, (cos A)² + (sin A)² = 1, из чего проистекает, пожалуй, наиболее важное тригонометрическое тождество.

Теорема: Для любого ∠A

cos² A + sin² A = 1

До сих пор все произвольные углы мы обозначали буквой A. Но это не значит, что вы обязаны всегда так делать, можно брать и другие буквы, например, x:

cos² x + sin² x = 1

В тригонометрии для этой цели часто используется греческая буква θ (тета) –

cos² θ + sin² θ = 1

А бывает и так, что вообще ничего не используется:

cos² + sin²= 1

Но перед тем как доказывать какое бы то ни было тождество, нужно найти длину отрезка прямой. В этом нам поможет теорема Пифагора.

Теорема (формула расстояния между двумя точками): Обозначим длину отрезка прямой от точки (x₁, y₁) до точки (x₂, y₂) буквой L. Тогда

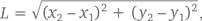
Например, длина отрезка от точки (–2, 3) до точки (5, 8) равна

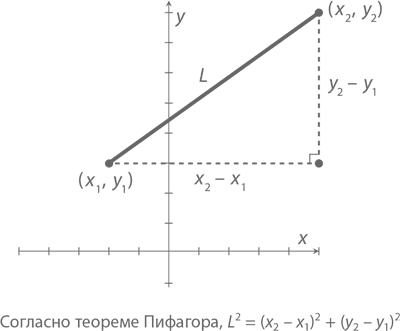
Доказательство: Возьмем две точки (x₁, y₁) и (x₂, y₂). Начертим прямоугольный треугольник, гипотенузой которого будет отрезок, соединяющий эти точки. На рисунке выше длина основания равна x₂ – x₁, а высота – y₂ – y₁. Следовательно, согласно теореме Пифагора, гипотенуза L равна

L² = (x₂ – x₁)² + (y₂ – y₁)²

то ес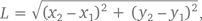ть

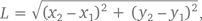что и требовалось доказать.

Отступление
Чему будет равна диагональ в коробке размером a × b × c? Возьмем прямоугольник, образующий дно этой коробки, и обозначим пару противоположных его углов буквами O и P. Длина и ширина при этом будут равны соответственно a и b, а диагональ OP – √(a² + b²).

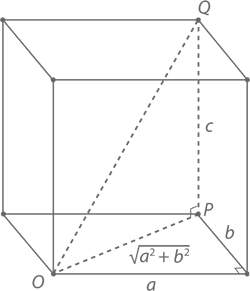
Теперь проложим линию c от точки P к точке Q, образующей угол, противолежащий O. Чтобы найти расстояние от O до Q, нам понадобятся длины катетов прямоугольного треугольника и c. Применим к ним теорему Пифагора и получим, что длина диагонали OQ равна

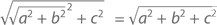
Ну а теперь собственно тождество – столь же полезное, сколь и красивое. Доказательство может показаться несколько запутанным, поэтому можете смело его пропускать (хотя я все же советую вам в нем разобраться – оно ляжет в основу доказательства других тождеств).

Теорема: Для любых углов A и B

cos(A – B) = cos A cos B + sin A sin B

Доказательство: На единичной окружности, центром которой является точка O, расположены точки P (cos A, sin A) и Q (cos B, sin B). Предположим, что длина отрезка PQ равна с. Что можно сказать о ней?

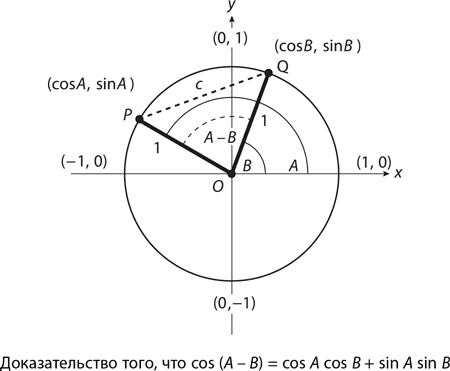
В треугольнике OPQ отрезки OP и OQ являются радиусами единичной окружности, а значит, их длина равна 1, а ∠POQ может быть измерен как A – B. Следовательно, согласно закону косинусов,

c² = 1² + 1² – 2(1)(1) cos (A – B) = 2 – 2 cos (A – B)

С другой стороны, формула расстояния приводит нас к уравнению

c² = (x₂ – x₁)² + (y₂ – y₁)²

поэтому расстояние c от точки P = (cos A, sin A) до точки Q = (cos B, sin B) соответствует

c² = (cos B – cos A)² + (sin B – sin A)² = cos² B – 2 cos A cos B + cos² A + sin² B – 2 sin A sin B + sin² A = 2 – 2 cos A cos B – 2 sin A sin B

где последнее представление основывается на уравнениях cos² B + sin² B = 1 и cos² A + sin² A = 1.

Соединив эти уравнения для c², получаем

2 – 2 cos (A – B) = 2 – 2 cos A cos B – 2 sin A sin B

Вычтем из обеих частей 2, разделим их на –2 и получим

cos (A – B) = cos A cos B + sin A sin B

что и требовалось доказать.◻

Отступление
Формула для cos (A – B) основывается на законе косинусов и исходит из того, что 0° < A – B < 180°. Но ту же теорему можно доказать и выйдя за рамки подобных ограничений. Если переместить треугольник POQ по часовой стрелке на B градусов, мы получим конгруэнтный ему треугольник P'OQ', в котором Q' будет располагаться на оси x в координатах (1, 0).

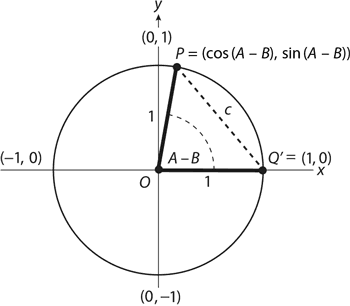
Так как ∠P'OQ' = A – B, P' = (cos (A – B), sin (A – B)). Согласно формуле расстояния для P'Q' будет верно следующее:

c² = (cos (A – B) – 1)² + (sin (A – B) – 0)² = cos² (A – B) – 2 cos (A – B) + 1 + sin² (A – B) = 2 – 2 cos (A – B)

Из этого можно заключить, что c² = 2 – 2 cos (A – B), при этом нам не нужны ни теорема косинусов, ни предположение об угле A – B. Ну а дальнейшее доказательство можно скопировать с предыдущего.

Обратите внимание, что при A = 90° формула для cos (A – B) утверждает следующее:

cos (90° – B) = cos 90° cos B + sin 90° sin B = sin B

Происходит это на том основании, что cos 90° = 0, а sin 90° = 1. Если в этом уравнении заменить B на 90° – B, получим

cos B = cos 90° cos (90° – B) + sin 90° sin (90° – B) = sin (90° – B)

Мы уже доказали правдивость этих утверждений на примере B как острого угла. Однако алгебра позволяет нам пойти дальше и подтвердить их для любого значения B. Так, если заменить B на – B, мы придем к

cos (A + B) = cos A cos (–B) + sin A sin (–B) = cos A cos B – sin A sin B

так как cos (–B) = cos B, а sin (–B) = –sin B. Если предположить, что B = A, у нас получится формула функций двойного угла:

cos (2A) = cos² A – sin² A

А так как cos² A = 1 – sin² A и sin² A = 1 – cos² A, мы также можем утверждать, что

cos (2A) = 1 – 2 sin² A и cos (2A) = 2 cos² A – 1

Из этого тождества косинусов проистекает аналогичное тождество синусов, например,

sin (A + B) = cos (90 – (A + B) = cos ((90 – A) – B) = cos (90 – A) cos B + sin (90 – A) sin B = sin A cos B + cos A sin B

B = A приводит нас к формуле функций двойного угла для синусов –

sin (2A) = 2 sin A cos A

а замена B на – B – к

sin (A – B) = sin A cos B – cos A sin B

Давайте соберем в одну таблицу все тождества, которые мы успели вывести в этой главе:

Повторюсь: использовать буквы A и B вы не обязаны, сгодятся и любые другие (скажем, cos (2u) = cos²u – sin²u или sin (2θ) = 2 sin θ cos θ).

Назад: Тригонометрия и окружность

Дальше: Радианы и графики в тригонометрии