Книга: Магия математики: Как найти x и зачем это нужно
Назад: Еще несколько закономерностей чисел Фибоначчи
Дальше: Рациональные и иррациональные числа
Глава номер шесть
Магия доказательств
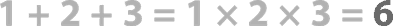
Ценность доказательств
Одна из главных радостей занятий математикой – возможность окончательных, не оставляющих ни тени сомнения доказательств. Это ставит математику на особое место в ряду других наук, которые опираются на соответствие законам материального мира. Однако новые открытия могут опровергать или изменять эти законы. В математике же доказанное однажды остается доказанным навсегда. Прошло больше 2000 лет с того момента, как Евклид доказал бесконечность множества простых чисел – и это никогда не удастся оспорить. Научно-технические формации сменяют друг друга, теоремы же вечны. Как однажды сказал великий Годфри Харди: «Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они сотканы из идей». По-моему, доказать новую теорему – все равно что шагнуть на тропу, ведущую в научное бессмертие.
В математике доказывают не только абсолютную истинность, но и невозможность. Часто приходится слышать: «Нельзя доказать невозможное». Полагаю, здесь имеется в виду, что никому не под силу доказать существование розовых коров – по крайней мере, до тех пор, пока мы не увидим их в один прекрасный день. Но в математике невозможное вполне себе доказуемо. Например, сколько ни пытайтесь, вы ни за что не найдете два четных числа, которые в сумме давали бы нечетное. Или простое число, которое было бы больше всех остальных простых чисел. Сложность таких доказательств поначалу пугает, к ним нужно привыкнуть, и не ждите, что это произойдет с первого (а то и со второго или с третьего) раза. Но стоит войти во вкус – и удержаться уже невозможно: настолько они удивительны и притягательны. Стройное доказательство подобно хорошему анекдоту или уместной шутке – удовлетворение от него испытываешь ничуть не меньшее.
С вашего позволения, расскажу о первом своем опыте на этой стезе. В детстве двумя главными предметами моего обожания были настольные игры и загадки. Как-то раз мой друг предложил мне загадку, связанную с настольными играми, и, конечно, я был заинтригован. Он положил передо мной пустую шахматную доску размером 8 на 8 клеточек и 32 костяшки домино и спросил:
– Можешь выложить домино так, чтобы они закрыли всю доску?
– Конечно, – уверенно ответил я. – Просто по четыре костяшки на ряд. Вот так:

– Молодец, – сказал он. – А если я уберу две клетки – правую нижнюю и левую верхнюю, и их останется 62 – сможешь закрыть оставшиеся 31 костяшкой? – и он положил на крайние квадратики две монетки.

– Хм… Наверное, – ответил я.
Но как я ни пытался, какие комбинации ни пробовал, у меня ничего не получалось. Наконец я сдался, заявив, что это в принципе невозможно.
– А если невозможно, – сказал мой друг, – можешь доказать это?
Я не мог. Ведь для этого потребовалось бы проверить бесконечное множество вариантов (если хотите, можете посчитать, сколько именно) и удостовериться в том, что каждый из них невозможен.
– Посмотри на цвета, – посоветовал друг, видя мое замешательство.
«На цвета? Причем тут цвета?» – подумал я. А потом понял. Обе закрытые клеточки были белыми, а значит, из 62 оставшихся свободными, 32 были черными и всего лишь 30 – белыми. А поскольку костяшка домино, как ее ни положи, закрывает пару разноцветных клеточек, выложить ими всю доску не получилось бы ни за что на свете. Здо́рово!
Отступление
Если вам понравилось последнее доказательство, понравится и это. Играя в известный всем «Тетрис», нужно заполнять «стакан» из 10 клеток падающими фигурами. Всего их 7, и соответственно их форме их иногда обозначают латинскими буквами: I, J, L, O, Z, T и S.
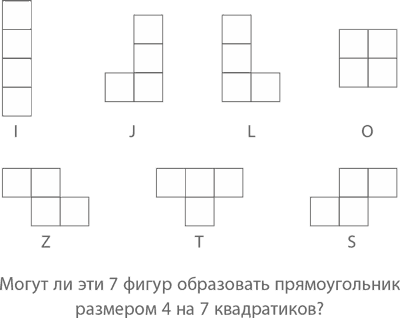
Каждая фигура состоит из 4 квадратиков, поэтому вполне естественно задаться вопросом, можно ли сложить их как-нибудь так, чтобы получился прямоугольник размером 4 на 7? При этом фигурки можно переворачивать как угодно.Оказывается, нельзя. Как это доказать? Давайте раскрасим квадратики в прямоугольнике в шахматном порядке – так, чтобы получилось 14 серых и 14 белых.

Обратите внимание: любая фигура, кроме «Т», должна закрывать 2 белых и 2 серых квадратика независимо от своего положения. Сама же «Т» состоит из 3 квадратиков одного цвета и 1 квадратика – другого. Следовательно, как бы ни располагались остальные 6 фигур, они закроют 12 белых и 12 серых квадратиков, а это значит, что для «Т» останется только по 2 квадратика каждого цвета, в которые она «не впишется».
Как же убедить окружающих в истинности математического утверждения, которое кажется нам верным? Обычно начинают с описания математических объектов, которые мы используем, например целых чисел
…, –2, –1, 0, 1, 2, 3…
множества, которое включает положительные и отрицательные числа и ноль.
Определив объекты, мы делаем допущение, которое считаем самоочевидным – например, «сумма или произведение двух целых чисел всегда будет целым числом» (в следующей главе, посвященной геометрии, мы будем исходить из того, что между двумя точками можно провести только одну прямую). Такие самоочевидные, не требующие доказательств утверждения называются аксиомами. С их помощью, плюс немного логики и алгебры, мы можем доказывать другие положения, не столь очевидные – теоремы. В этой главе вы познакомитесь с основным инструментарием математических доказательств.
Начнем, пожалуй, с доказательства простых теорем, которые вызывают минимум сомнений. Когда мы слышим «два четных числа при сложении дают третье четное число» или «два нечетных числа при умножении дают третье нечетное число», наш разум обычно пытается проверить такие утверждения рядом примеров и из них сделать вывод, что это, скорее всего, верно. Ну или хотя бы не полная чушь. Вы даже можете решить, что это настолько очевидно, что может быть принято как аксиома. Делать этого не стоит – по крайней мере, до тех пор, пока вы можете построить цепочку доказательств, используя уже известные вам аксиомы. Так, чтобы доказать утверждения о четных и нечетных числах, начать стоит с понимания того, что вообще такое «четное» и «нечетное».
Четным называется число, которое делится на 2 без остатка. Если выразить это алгебраически, то число n является четным, если n = 2k (где k есть целая величина). Будет ли четным числом 0? Да, потому что 0 = 2 × 0. Теперь у нас есть все необходимое, чтобы доказать, что два четных числа в сумме дают третье четное.
Теорема: Если m и n – четные, то сумма m + n – тоже четное.
Это прекрасный пример теоремы по принципу «если…, то…». Чтобы ее доказать, нам надо сделать допущение в части, начинающейся с «если…», и, смешав логику с алгеброй, показать, что часть, начинающаяся с «то…», является следствием этого допущения. В нашем примере мы предполагаем, что m и n – четные, и поэтому m + n тоже будет четным.
Доказательство: Предположим, что m и n – четные числа. Значит, m = 2j, а n = 2k, где j и k суть целые величины. Тогда
m + n = 2j + 2k = 2(j + k)
А так как j + k – целое, m + n тоже будет кратно 2, значит, оно четное.◻
Обратите внимание, что доказательство основывается на аксиоме, согласно которой сумма двух целых чисел (в нашем случае j + k) так же является целым числом. Очень часто уже доказанные простые теоремы закладывают основу доказательной базы теорем более сложных, элементарные же аксиомы отбрасываются за ненадобностью. У математиков, кстати, принято ставить в конце последней линии цепочки доказательств значок ◻ или ■ либо аббревиатуру «ч.т.д.» – «что и требовалось доказать». (Также встречается аббревиатура Q.E.D., происходящая от латинской фразы «quod erat demonstrandum», «что и должно было быть продемонстрировано», ну или от английской «quite easily done», «ничего сложного» – выбирайте вариант по душе.) Я, с вашего позволения, буду иногда использовать еще один символ, смайлик ☺, когда доказательство покажется мне особенно стройным и красивым.
Редкий математик устоит перед тем, чтобы, доказав теорему по принципу «если…, то…», не попытаться доказать ее же, но наоборот, используя в качестве отправной точки обратное высказывание, то есть, по сути, меняя местами части «если…» и «то…». В нашем примере с четными числами обратным высказыванием станет предположение, что «если m + n является четным числом, то m и n также будут четными числами». Ошибочность его можно доказать контрпримером. Это несложно, буквально элементарно, как
1 + 1 = 2
где очень четко и ясно видно, что четное число можно получить сложением двух других чисел, которые четными не являются.
Следующая наша теорема касается нечетных чисел. Нечетным называется такое число, которое не делится на 2. Попытавшись это сделать, вы всегда получите 1 в остатке. Алгебраически n является нечетным, если n = 2k + 1, где k – целое число. Этого нам вполне хватит, чтобы доказать, что при умножении двух нечетных чисел мы получим третье нечетное.
Теорема: Если m и n – нечетные, то их произведение mn также будет нечетным.
Доказательство: Предположим, что m и n являются нечетными числами. Тогда m = 2j + 1, а n = 2k + 1 при целых значениях j и k. Тогда, согласно правилу FOIL,
mn = (2j + 1)(2k +1) = 4jk + 2j + 2k + 1 = 2(2jk + j + k) + 1
А так как 2jk + j + k – целое число, то mn есть форма «удвоенного целого числа + 1», а значит, нечетное число.◻
А что насчет обратного высказывания? Итак, если mn – нечетное, будут ли так же нечетными m и n? Будут, и подтвердить это можно, используя доказательство от противного. Для этого нам нужно показать, что опровержение части «то…» (что m и n суть нечетные) приведет к ошибке, причем не только во второй, но и в первой части «если…». Что и подтвердит довольно странным, но вполне логичным образом наше предположение.
Теорема: Если mn – нечетное, то и m и n будут также нечетными.
Доказательство: Предположим, что либо m, либо n (или оба) – четные числа. Выберем m (хотя по большому счету это не важно). Значит, m = 2j при целом значении j. Тогда произведение mn = 2jn также получится четным, что противоречит изначальному условию.◻
В том случае, когда теорему можно доказать как в «прямом», так и в «обратном» порядке, ее иногда называют теоремой по принципу «если и только если» (или «тогда и только тогда»). Как раз такую мы сейчас и доказали:
Теорема: m and n являются нечетными, если и только если mn – нечетное («…тогда и только тогда, когда mn – нечетное»).

