Книга: Магия математики: Как найти x и зачем это нужно
Назад: Ценность доказательств
Дальше: Доказательство методом индукции
Рациональные и иррациональные числа
Возможно, теоремы, которые мы только что рассмотрели, ничем вас не удивили, а их доказательства показались вам весьма прямолинейными. Куда большее удовольствие получаешь, пытаясь подтвердить менее очевидные предположения. Пока что мы довольствовались целыми числами – не пора ли заняться дробями? Число, которое можно представить в дробном виде, называется рациональным. Если быть точным, то число r является рациональным, если r = a/b, где a и b – целые числа, а b ≠ 0. Например, 23/58, –22/7 или 42 (равное, по сути, 42/1) – числа рациональные. Если же число не является рациональным, его называют иррациональным. Яркий тому пример, о котором вы, наверняка, слышали – число π = 3,14159…, но о нем чуть позже, в главе 8.
Для следующей нашей теоремы не лишним будет вспомнить, как вообще складывать дроби. И легче всего это делать, когда дроби имеют общий знаменатель, например:
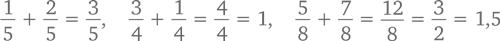
В противном случае нам сперва придется привести дроби к общему знаменателю:
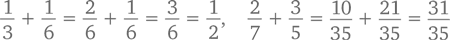
В целом же дроби a/b и c/d можно привести к общему знаменателю таким вот нехитрым способом:
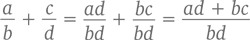
И этого вполне достаточно, чтобы доказать несколько простых теорем, связанных с рациональными числами.
Теорема: Среднее арифметическое двух рациональных чисел также будет рациональным числом.
Доказательство: Возьмем два рациональных числа – x и y. Значит, в равенствах x = a/b и y = c/d значения a, b, c и d суть целые числа. Среднее арифметическое x и y, таким образом, можно представить как
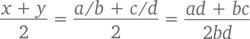
Это дробь, числитель и знаменатель которой – целые числа. Следовательно, среднее арифметическое значение x и y является рациональным числом.
А теперь давайте подумаем, что же именно утверждается в этой теореме. А утверждается в ней то, что между двумя разными рациональными числами, насколько бы близки они друг другу ни были, всегда найдется еще одно рациональное число. Возникает искушение сделать из этого вывод, что все числа являются рациональными (как довольно долго думали древние греки). Нет, это не так. И смотрите, почему. Возьмем число √2, которое в десятичной записи выглядит как 1,4142… Если мы попробуем записать его как обычную дробь, получится что-нибудь вроде 10/7 или 1414/1000 (вариантов огромное множество), но все они будут приблизительными и никогда при возведении в квадрат не дадут 2. Но что, если мы просто плохо ищем? Да нет, не плохо, и следующая наша теорема как раз и показывает, что любые такие поиски бесполезны по определению. Доказательство будет строиться от противного, как это обычно и бывает, когда разговор заходит об иррациональных числах. А заодно мы увидим, как сократить дробь до ее несократимого значения – того предела, когда у числителя и знаменателя остается только один общий делитель – 1.
Теорема:√2 есть иррациональное число.
Доказательство: Предположим обратное: √2 есть число рациональное. В таком случае существуют некие положительные целые числа a и b, для которых верно, что
√2 = a/b
где дробь a/b – несократимая. Возведя обе части уравнения в квадрат, получим
2 = a²/b²
или
a² = 2b²
что приводит нас к тому, что a² есть четное целое число. А если a² – четное, значит, четным является и a (по аналогии с недавним нашим доказательством того, что, если нечетное a умножить на само себя, результат будет также нечетным). То есть a = 2k, где k – целое число. Добавим это в свое уравнение и получим
(2k)² = 2b²
То есть
4k² = 2b²
что приводит нас к
b² = 2k²
и констатации того факта, что b² является четным числом. Значит, четным должно быть и b. Но постойте! Ведь при четных значениях как a, так и b дробь a/b никак не может быть несократимой! Это противоречит нашим исходным условиям. И завело нас в эту ловушку предположение, что √2 является рациональным числом. Поэтому нам не остается ничего иного, кроме как признать: число √2 – иррациональное.☺
Лично я нахожу это доказательство восхитительным (и смайлик в конце строки тому подтверждение): прямая и хорошо освещенная тропа чистой, ничем не замутненной логики приводит нас к удивительному умозаключению. В главе 12 мы еще увидим, насколько велик на самом деле процент иррациональных чисел. Практически все действительные числа являются иррациональными, притом, что в повседневной жизни мы с ними почти не сталкиваемся.
Из доказанной нами только что теоремы следует одно любопытное заключение (его, пожалуй, даже можно назвать сопутствующей теоремой – такой, условия которой вытекают из только что доказанной). Основано оно на следующем правиле возведения в степень, согласно которому для любых положительных значений a, b и c
(ab)c = abc
То есть утверждение, что (5³)² = 56, будет вполне справедливым, потому что
(5³)² = (5 × 5 × 5) × (5 × 5 × 5) = 56
Сопутствующая теорема: Существуют иррациональные числа a и b, при которых число ab будет рациональным.
Не пугайтесь, нам эта теорема вполне по плечу, хоть мы и знаем пока лишь одно иррациональное число – √2. Приведенное ниже доказательство является, по сути, доказательством существования: мы же пытаемся просто узнать, есть ли вообще такие a и b, а не определить их конкретные числовые выражения.
Доказательство: Раз уж мы знаем, что √2 является иррациональным числом, возьмем число 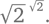 Будет ли оно рациональным? Если да, то теорема доказана (поскольку и a и b равны √2). Если нет – что ж, по крайней мере мы узнаем еще одно иррациональное число
Будет ли оно рациональным? Если да, то теорема доказана (поскольку и a и b равны √2). Если нет – что ж, по крайней мере мы узнаем еще одно иррациональное число  примем
примем 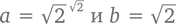 и с помощью правила возведения в степень получим
и с помощью правила возведения в степень получим
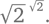 Будет ли оно рациональным? Если да, то теорема доказана (поскольку и a и b равны √2). Если нет – что ж, по крайней мере мы узнаем еще одно иррациональное число
Будет ли оно рациональным? Если да, то теорема доказана (поскольку и a и b равны √2). Если нет – что ж, по крайней мере мы узнаем еще одно иррациональное число  примем
примем 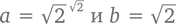 и с помощью правила возведения в степень получим
и с помощью правила возведения в степень получим
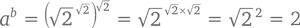
то есть рациональное число. Следовательно, независимо от того, является  рациональным или иррациональным числом, мы докажем, что ab будет рациональным числом при иррациональных значениях a и b.☺
рациональным или иррациональным числом, мы докажем, что ab будет рациональным числом при иррациональных значениях a и b.☺
 рациональным или иррациональным числом, мы докажем, что ab будет рациональным числом при иррациональных значениях a и b.☺
рациональным или иррациональным числом, мы докажем, что ab будет рациональным числом при иррациональных значениях a и b.☺Так обычно и выглядит любое доказательство существования чего бы то ни было: почти всегда остроумно и очень редко – исчерпывающе. (Кстати, уж коли зашла речь: число  – все-таки иррациональное число, но сейчас это для нас абсолютно не принципиально.)
– все-таки иррациональное число, но сейчас это для нас абсолютно не принципиально.)
 – все-таки иррациональное число, но сейчас это для нас абсолютно не принципиально.)
– все-таки иррациональное число, но сейчас это для нас абсолютно не принципиально.)Куда больше удовлетворения (равно как и куда больше существенной информации) получаешь, идя путем конструктивного доказательства. Одно из них, к примеру, – доказательство того, что любое рациональное число a/b либо вовсе не имеет цифр после запятой, либо эти цифры повторяются (иными словами, в затянувшемся делении b раз за разом становится делителем того числа, что уже делилось). Но будет ли верным обратное? Само собой, конечная десятичная дробь должна быть рациональным числом. Например, 0,12358 = 12 358/100 000. А если эта дробь – допустим, 0,123123123… – периодическая? Должна ли она быть рациональным числом? Ответ – да, и вот вам очень элегантный способ это доказать. А заодно и найти это самое число. Обозначим искомое буквой w (как в английском слове waltz, которое означает «проще простого»), то есть
w = 0,123123123…
Умножим обе части на 1000:
1000w =123,123123123…
вычтем первое уравнение из второго:
999w = 123
и получим
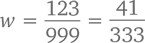
Возьмем еще одну периодическую десятичную дробь, но на этот раз такую, в которой цикл повторения начинается не с первой после запятой цифры, а чуть позже.
Какой обычной дроби будет соответствовать десятичная 0,83333…? Начнем с
х = 0,83333…
Затем сделаем так:
100x = 83,3333…
и так:
10x = 8,3333…
При вычитании 10x из 100x все, что стоит после запятой, отсекается, оставляя нас с
90x = (83,3333…) – (8,3333…) = 75
Значит,
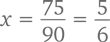
Этот алгоритм позволяет нам с определенной долей уверенности утверждать, что число будет рациональным тогда и только тогда, когда его представление в виде десятичной дроби является либо конечным, либо периодическим. Иррациональной же будет та дробь, которая после запятой имеет бесконечное количество знаков, не образуюющих при этом цикл, например,
v = 0,123456789101112131415…
Назад: Ценность доказательств
Дальше: Доказательство методом индукции

