Еще несколько закономерностей чисел Фибоначчи

Книга: Магия математики: Как найти x и зачем это нужно

Назад: Подсчет с помощью чисел Фибоначчи

Дальше: Глава номер шесть Магия доказательств

Говоря о треугольнике Паскаля, мы видели, насколько красивые в своей сложности закономерности демонстрируют его четные и нечетные числа. С последовательностью Фибоначчи все проще. Посмотрите на нее еще раз. Какие из этих чисел четные?

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

F₃ = 2, F₆ = 8, F₉ = 34, F₁₂ = 144 и т. д. (в этом разделе мы снова переключимся на заглавную F, чтобы подчеркнуть красоту и значительность описанных здесь закономерностей). Позиции четных чисел – 3, 6, 9 и 12. Похоже, что интервал между ними всегда равен 3. Доказать это очень легко, достаточно просто проследить закономерность с самого начала последовательности:

нечетное, нечетное, четное

И дальше такой порядок повторяется вновь и вновь:

нечетное, нечетное, четное, нечетное, нечетное, четное, нечетное, нечетное, четное…

Происходит это потому, что после каждого блока «нечетное, нечетное, четное» следующий цикл сложения выглядит как «нечетное + четное = нечетное», потом «четное + нечетное = нечетное» и, наконец, «нечетное + нечетное = четное», так что закономерность бесконечно повторяется.

Говоря языком соотносимости, выученным нами в главе 3, каждое четное число соотносится с 0 (по модулю 2), а каждое нечетное – с 1 (также по модулю 2), а 1 + 1 ≡ 0 (mod 2). Вот как выглядит последовательность Фибоначчи в двоичной системе (или по модулю 2 – выбирайте любой термин):

1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0…

А что насчет чисел, кратных 3? Первые из них – F₄ = 3, F₈ = 21, F₁₂ = 144, что волей-неволей наталкивает нас на мысль, что кратные 3 числа занимают в последовательности каждое четвертое место. Чтобы эту догадку подтвердить, заменим все числа Фибоначчи на 0, 1 или 2 и будем считать по модулю 3, где

1 + 2 ≡ 0, а 2 + 2 ≡ 1 (mod 3)

В троичной системе последовательность выглядит как

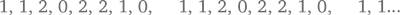
После каждого восьмого числа мы замыкаем круг и начинаем опять с двух следующих друг за другом единиц, то есть в этом случае цикл состоит из 8 чисел, четвертое и восьмое из которых – 0. Так и получается, что каждое четвертое место последовательности Фибоначчи занято числом, кратным 3. Считая по модулю 5, 8 или 13, обнаруживаем, что

Каждое пятое число последовательности кратно 5
Каждое шестое число последовательности кратно 8
Каждое седьмое число последовательности кратно 13

и закономерность продолжается.

А что насчет чисел, следующих друг за другом? Есть ли между ними что-то общее? Что интересно – в каком-то смысле ничего общего между ними нет. И мы можем это продемонстрировать. Пары чисел, находящихся рядом в последовательности

(1, 1), (1, 2), (2, 3), (3, 5), (5, 8), (8, 13), (13, 21), (21, 34)…

называются взаимно простыми, что означает, что нет числа, большего чем 1, на которое они оба делятся. Если мы возьмем для примера последнюю из перечисленных выше пар, мы увидим, что 21 делится на 1, 3, 7 и 21, а 34 – на 1, 2, 17 и 34. То есть у 21 и 34 только один общий делитель – 1. Как убедиться, что эта закономерность повторяется? Откуда нам знать, что числа следующей пары (34, 55) – непременно взаимно простые? Для этого необязательно искать все делители для 55. Пойдем от обратного: предположим, что есть некое число d > 1, на которое и 34, и 55 делятся без остатка. Но тогда на него должна делиться без остатка и их разность: 55 – 34 = 21 (если два числа кратны третьему, их разность тоже будет ему кратна), что невозможно: ведь мы уже знаем, что нет такого d > 1, на которое можно было бы разделить и 21, и 34. Раз за разом применяя это доказательство, мы придем к выводу, что все числа последовательности Фибоначчи, образующие пары по принципу ближайшего соседства, являются взаимно простыми.

А теперь – мой самый любимый факт о числах Фибоначчи. Он касается наибольшего общего делителя (НОД). Наибольший общий делитель двух чисел есть наибольшее число, на которое делятся оба эти числа. Например, для 20 и 90 НОД равен 10. Обозначается это как

НОД(20, 90) = 10

Как вы думаете, каким будет наибольший общий делитель двадцатого и девяностого чисел последовательности Фибоначчи? Ответ звучит как поэзия: 55 – десятое число последовательности Фибоначчи! А вот уравнение:

НОД(F₂₀, F₉₀) = F₁₀

Или в общем виде, для значений m и n:

НОД(F_m, F_n) = F_{НОД(m; n)}

Другими словами, «НОД значений F есть значение F НОДа»! Подробно останавливаться на этом мы здесь не будем, но и пройти мимо я не мог.

Иногда закономерность может оказаться обманчивой. Какие, например, из чисел Фибоначчи являются простыми? (Простые – это числа больше 1, которые при этом делятся без остатка только на 1 и на самих себя, мы поговорим о них подробнее в следующей главе.) Числа больше единицы, не являющиеся простыми, называются составными, потому что их можно разложить на неделимые простые составляющие. Вот несколько первых простых чисел последовательности Фибоначчи:

2, 3, 5, 7, 11, 13, 17, 19…

А теперь взгляните на числа, стоящие на «простых» позициях:

F₂ = 1, F₃ = 2, F₅ = 5, F₇ = 13, F₁₁ = 89, F₁₃ = 233, F₁₇ = 1597

Числа 2, 5, 13, 89, 233 и 1597 – простые. Закономерность вроде бы говорит нам о том, что, если значение p > 2 является простым, простым будет и F_p. Однако следующий же элемент последовательности эту закономерность нарушает: F₁₉ = 4181 – уже составное число, потому что 4181 = 37 × 113. Но верно и то, что каждое простое число больше 3 стоит в последовательности Фибоначчи на «простой» позиции. Это следует из одной из уже рассмотренных закономерностей. F₁₄ должно быть составным, поскольку каждое седьмое число последовательности кратно F₇ = 13 (и правда: F₁₄ = 377 = 13 × 29).

На самом деле простые числа Фибоначчи встречаются редко – пока что официально подтверждено лишь 33, наибольшее из них занимает F₈₁₈₃₉ позицию. И это притом, что вопрос, является ли количество простых чисел в последовательности бесконечным, еще не решен.

Но отвлечемся немного от серьезных научных изысканий и займемся небольшим, но забавным фокусом, основанным на магии чисел Фибоначчи.

В 1 и 2 рядах таблицы напишите два любых числа от 1 до 10. Сложите их, а сумму запишите в 3 ряду. Затем сложите числа из 2 и 3 рядов. Результат запишите в 4 ряд. Продолжайте так делать (ряд 3 + ряд 4 = ряд 5 и т. п.), пока не дойдете до конца таблицы. У вас получится свой вариант последовательности Фибоначчи. А теперь разделите число из 10 ряда на число из 9 ряда. Из результата вам нужны первые три цифры, включая те, которые идут после запятой. В нашем примере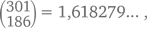

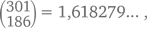из них оставляем 1,61. Хотите – верьте, хотите – нет, но, с каких бы двух положительных (необязательно целых и даже необязательно из промежутка от 1 до 10) чисел в 1 и 2 рядах вы ни начали, частным при делении числа 10 ряда на число 9 ряда всегда будет 1,61. Попробуйте сами разок-другой и легко в этом убедитесь.

Чтобы разобраться в природе этого фокуса, обозначим первые два числа литерами x и y. Тогда, следуя методу Фибоначчи, получаем x + y в 3 ряду, y + (x + y) = x + 2y в 4-м и т. д. по таблице:

Требуется найти частное чисел 10 и 9 рядов:

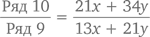
Почему же результат всегда будет начинаться с 1,61? Вы удивитесь, но в основе этого лежит неправильное сложение дробей. Допустим, у нас есть две дроби: a/b и c/d, причем знаменатели b и d – положительные величины. Что будет, если сложить между собой сначала числители, а потом знаменатели? А будет то, что получившееся в результате число, называемое медиантой, всегда будет где-то между двух исходных дробей. То есть при любых дробях a/b < c/d, знаменатели которых суть положительные величины, имеем

Начиная, например, с дробей 1/3 и 1/2, для которых медианта будет 2/5, она расположена в интервале 1/3 < 2/5 < 1/2.

Отступление
Почему медианта всегда будет располагаться примерно между изначальными числами? Если мы начинаем с дробей где b и d – положительные величины, ad будет меньше bc. Прибавив к обеим сторонам ab, получим ab + ad < ab + bc или a(b + d) < (a + c)b, что значит, что Таким же образом приходим к

Обратите внимание, что при x, y > 0

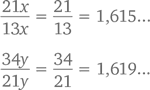
Следовательно, медианта этих двух дробей должна находиться между ними. Другими словами,

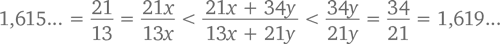
Вот почему частное чисел из 10 и 9 рядов должно начинаться с 1,61, как мы уже до этого и посчитали.

Отступление
Прежде чем открыть секрет числа 1,61, можете поразить свою аудиторию, постоянно добавляя числа к своей таблице. Так, в нашем примере, где мы начали с 3 и 7, достаточно беглого взгляда, чтобы узнать результат – 781. Как? С помощью алгебры. Если сложить значения из 2 таблицы, мы получим сумму, равную 55x + 88y. И что? А то, что вместо этого можно написать 11(5x + 8y) = 11 × ряд 7. Поэтому, взяв число из 7 ряда (в нашем примере это 71) и умножив его на 11 (здесь можно использовать фокус с умножением на 11 из главы 1), получим 781.

В чем важность числа 1,61? Если не останавливаться на 10 ряду и продолжать расширять таблицу, вы легко обнаружите, что частное двух соседних чисел будет от ряда к ряду все больше приближаться к значению, которое называют «золотым сечением» –

Кроме g, для обозначения этого числа математики часто используют греческую букву φ, которая произносится как «фи» (да-да, «Фи-боначчи»).

Отступление
Алгебра покажет нам, на самом ли деле частное двух соседних чисел последовательности Фибоначчи приближается к g. Предположим, что частное F_n+1/F_n приближается к значению r при увеличении n. Но ведь о числах Фибоначчи мы знаем, что F_n+1 = F_n + F_n–1, поэтому

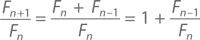
При увеличении значения n левая сторона приближается к r, а правая – к Значит,

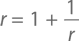
Умножив обе стороны этого уравнения на r, получим

r² = r + 1
Другими словами, r² – r – 1 = 0, а согласно формуле корней квадратного уравнения здесь имеется только один положительный ответ:

Существует еще одна будоражащая воображение формула для n-ного числа последовательности Фибоначчи, которая использует золотое сечение. Это формула Бине, которая говорит, что

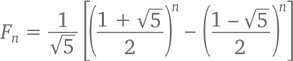
Глядя на нее, я не перестаю удивляться: как такое возможно, что вся эта формула, построенная вокруг √5, приводит к целым величинам?!

Мы можем ее немного упростить, потому что значение

находится между –1 и 0, и чем больше мы увеличиваем степень, тем больше оно приближается к 0. По большому счету, можно утверждать, что для любого n ≥ 0, F_n вычисляется через gⁿ/√5 с последующим округлением до ближайшего целого. Можете взять калькулятор и проверить. Если взять g = 1,618, то, возведя 1,618 в десятую степень, получим 122,966… (что подозрительно близко к 123). А разделив этот результат на √5 ≈ 2,236, придем к 54,992. Округление даст F₁₀ = 55 – известный нам результат. Из g²⁰ получается 15 126,99993, которое после деления на √5 превращается в 6765,00003, то есть F₂₀ = 6765. А калькулятор легко проведет нас от g¹⁰⁰/√5 к F₁₀₀ ≈ 3,54 × 10²⁰.

Все эти вычисления показывают, что g¹⁰ и g²⁰ настолько близки к целым числам, что практически ими являются. Что именно здесь происходит? Посмотрите на последовательность Люка́

1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521…

названную в честь французского математика Эдуарда Люка (1842–1891) – первооткрывателя многих удивительных свойств этих чисел, а заодно и чисел Фибоначчи, включая формулу с наибольшим общим делителем, о которой мы не так давно говорили. Кстати, именно Люка впервые назвал набор чисел 1, 1, 2, 3, 5, 8… последовательностью Фибоначчи. Последовательность же Люка соответствует его собственной (несколько упрощенной) версии формулы Бине –

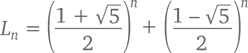
Другими словами, при n ≥ 1 L_n есть целая ближайшая к g_n величина (что согласуется с тем, что мы уже видели: g¹⁰ ≈ 123 = L₁₀). А вот как связаны между собой последовательности Фибоначчи и Люка:

Не заметить здесь закономерность почти невозможно. Например, сложение «соседей» числа Фибоначчи дает соответствующее ему по позиции число последовательности Люка:

F_n_–1 + F_n₊₁ = L_n

А если мы сложим «соседей» числа из последовательности Люка, получим результат, который будет ровно в 5 раз больше соответствующего ему по позиции числа Фибоначчи:

L_n_–1 + L_n_–1 = 5F_n

Если перемножить между собой соответствующие друг другу числа двух последовательностей, мы получим еще одно число последовательности Фибоначчи!

F_n L_n = F_2n
Отступление
Последнее может быть доказано с помощью алгебры и формул Бине (а именно (x – y)(x + y) = x² – y²). Исходя из h = (1 – √5)/2, представим формулы Бине для чисел Фибоначчи и Люка в виде

И когда мы их перемножаем, получается

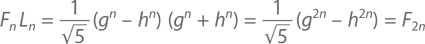
Откуда пришло название «золотое сечение»? Из золотого прямоугольника, в котором соотношение длинной и короткой сторон составляет g = 1,61803…

Если обозначить короткую сторону единицей и убрать из прямоугольника квадрат со сторонами 1 на 1, у нас останется еще один прямоугольник со сторонами 1 и (g – 1), соотношение которых составит

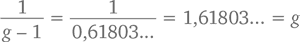
То есть пропорции маленького прямоугольника будут такими же, как и большого. Кстати, g – единственное в своем роде число со столь уникальными свойствами, потому что уравнение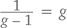

подразумевает, что g² – g – 1 = 0. А формула корней квадратного уравнения приводит нас только к одному положительному числу, удовлетворяющему этому условию, и число это – (1 + √5)/2 = g.

Благодаря этому своему свойству золотой прямоугольник считается эстетически образцовым, а потому часто используется в разных областях искусства, будь то живопись, фотография или архитектура. Например, Лука Пачоли – друг и соратник Леонардо да Винчи называл его «божественной пропорцией».

Золотое сечение лежит в основе стольких удивительных математических явлений, что подчас очень сложно удержаться от соблазна увидеть его даже там, где его нет и никогда не было. Например, в романе «Код да Винчи» Дэн Браун пишет, будто число 1,618 встречается везде и всегда, и подтверждение тому – строение человеческого тела, Браун утверждает, что отношение нашего роста к высоте, на которой расположен пупок, – 1,618. Я не проводил измерений, но в статье Джорджа Марковски «Выдумки о золотом сечении», опубликованной в журнале College Mathematics Journal, говорится, что это не соответствует реальности. Тем не менее каждый раз, когда где-то встречается число, хоть сколько-то близкое к 1,6, кто-нибудь вспоминает о золотом сечении.

Я уже не раз говорил, что многие числовые закономерности, в которых присутствуют числа Фибоначчи, суть настоящая поэзия. И это не просто метафора: эти числа действительно используются при создании стихотворений. Возьмем, к примеру, лимерики. Вот, последите за ритмом (пусть без слов, просто используя сетку слогов):

Если посчитать количество слогов в каждом ряду, мы получим числа Фибоначчи! Лично меня это вдохновило настолько, что я отважился написать о них свой собственный лимерик:

Ты с ними достигнешь вершин!
Сначала – «один» и «один»,
Потом – «два», «три», «пять»,
Продолжим считать –
Веселью положен почин!

Назад: Подсчет с помощью чисел Фибоначчи

Дальше: Глава номер шесть Магия доказательств