Мы заглянули лишь в замочную скважину той двери, за которой раскинулся сад самых настоящих чудес. Только растут в нем не деревья, а числовые закономерности, уходящие корнями в последовательность Фибоначчи. И вам, наверняка, не терпится узнать, для чего еще, кроме подсчета поголовья кроликов, нужны эти числа. На самом деле – много для чего. В 1150 году (задолго до того, как Леонардо Пизанский представил миру задачку про кроликов) индийский поэт Хемачандра задался очень интересным вопросом: сколькими способами можно сложить стихотворную стопу из n безударных или ударных слогов. Давайте сперва переведем эту проблему из плоскости поэзии в плоскость математики.

Вопрос: Сколькими способами можно записать число n как сумму единиц и двоек?

Ответ: Обозначим результат как f_n. Вот что будем иметь при стартовых значениях n:

У нас есть один вариант, дающий в сумме 1, два варианта, дающих 2 (1 + 1 и 2), и три варианта, дающих 3 (1 + 1 + 1, 1 + 2 и 2 + 1). Повторимся: для получения нужной нам суммы доступны только единицы и двойки. При этом порядок этих цифр имеет значение: 1 + 2 и 2 + 1 суть две разные комбинации. Получить 4 можно уже пятью разными вариантами: 1 + 1 + 1 + 1, 1 + 1 + 2, 1 + 2 + 1, 2 + 1 + 1, 2 + 2. По всему выходит, что числа в правой части нашей таблицы – это числа из последовательности Фибоначчи, и так оно есть на деле.

Давайте попробуем понять, почему вдруг 5 можно получить f5 = 8 различными способами. Начинаться сложение может с 1 или 2. Сколько вариантов будет начинаться именно с 1? За первой цифрой должна следовать некая комбинация 1 и 2, которая в сумме даст 4, а по предыдущей строке мы знаем, что таких комбинаций у нас f₄ = 5. Теперь так же посчитаем, сколько вариантов будет начинаться с 2. В этом случае комбинация после первой цифры должна давать нам 3. Смотрим чуть выше по таблице и видим, что f₃ = 3. Значит, общее количество комбинаций 1 и 2, дающих в сумме 5, должно быть 5 + 3 = 8. Тот же алгоритм приведет нас к тому, что для 6 таких комбинаций будет 13: f₅ = 8, начинающихся с 1, плюс f₄ = 5, начинающихся с 2. В целом же, для суммы n их число равно f_n, из которых f_n–1 имеют в начале 1, а f_n–2 – 2. Следовательно,

Причем все значения f_n дублируют числа последовательности Фибоначчи и будут и дальше их дублировать с увеличением значения n. Причина в том, что это и есть последовательность Фибоначчи, только в несколько измененном виде – с небольшим смещением. Обратите внимание, что f₁ = 1 = F₂, f₂ = 2 = F₃, f₃ = 3 = F₄ и т. д. (для удобства договоримся, что f₀ = F₁ = 1, а f_–1 = F₀ = 0). Обобщая, мы можем утверждать, что при n ≥ 1

А так как мы с вами уже знаем, что означают числа последовательности, мы с их помощью можем доказать состоятельность многих и многих других удивительных закономерностей. Возьмем, к примеру, ту из них, о которой мы говорили в конце главы 4, когда просчитывали диагонали Паскалева треугольника:

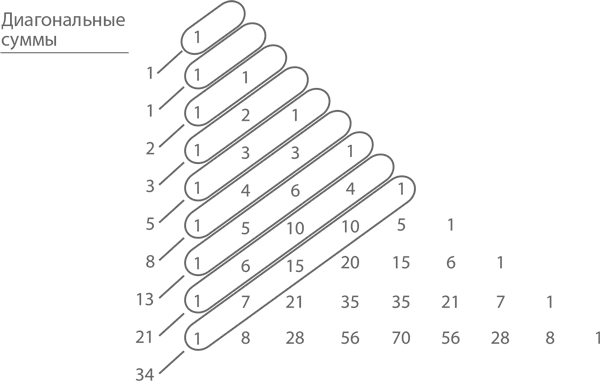
Так, восьмая диагональ дает нам

С точки зрения «подсчета комбинаций» это значит, что

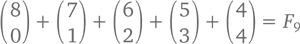
Чтобы понять суть этой закономерности, попробуем ответить на один вопрос двумя различными способами.

Вопрос: Сколько существует возможных комбинаций единиц и двоек, дающих в сумме 8?

Ответ номер один: Судя по тому, о чем мы говорили чуть выше, – f₈ = F₉.

Ответ номер два: Представим себе эту проблему как 5 частных задач, в основе каждой из которых лежит количество двоек в комбинации. Сколько комбинаций обойдется вообще без двоек? Разумеется, только одна – 11111111. И поэтому совсем не случайно, что

С одной двойкой? Уже семь: 2111111, 1211111, 1121111, 1112111, 1111211, 1111121, 1111112. Каждая из них состоит из семи цифр, и, смещая двойку шаг за шагом, получаем

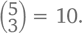С двумя двойками (скажем, 221111)? Не будем перечислять их все, просто отметим, что любая из них будет состоять из двух двоек и четырех единиц, то есть всего из шести цифр, что дает нам возможных местоположений двоек. По той же логике комбинации с тремя двойками будут включать в себя две единицы и состоять из 5 цифр, а общее их количество будет равняться И наконец, из четырех двоек у нас получится всего одна комбинация (а именно 2222), потому что

Оба ответа отлично проясняют всю ситуацию. И заодно объясняют, почему сумма чисел n-ной диагонали треугольника Паскаля равна одному из чисел последовательности Фибоначчи. То есть при n ≥ 0 сложение чисел диагонали n (вплоть до того момента, пока через n/2 шагов мы не выйдем за границы треугольника) дает нам

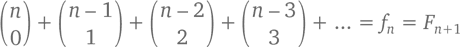
К тому же можно прийти, представив последовательность Фибоначчи в виде плиток черепицы. Тогда f₄ = 5 означает 5 способов выложить один ряд (условно состоящий из 4 квадратов) одинарными (в виде квадратов) и двойными (в виде прямоугольников) плитками. То есть 1 + 1 + 2 будет выглядеть как «квадрат – квадрат – прямоугольник».

Такую визуализацию можно использовать, чтобы понять другие закономерности, основанные на числах Фибоначчи. Давайте посмотрим, что произойдет, если возвести числа Фибоначчи в квадрат.

В том, что, сложив два соседних числа последовательности Фибоначчи, мы получим следующее за ними, ничего нового для нас нет (в конце концов, именно так и появилась эта последовательность). А теперь посмотрите на числа Фибоначчи, возведенные в квадрат и сложенные между собой:

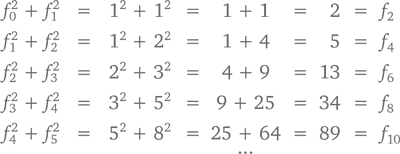
Попробуем объяснить эту закономерность с точки зрения счета. Последнее уравнение утверждает, что

Почему? Ответим на простой вопрос.

Вопрос: Сколькими способами можно выложить из квадратов и прямоугольников ряд длиной в 10 квадратов?

Ответ 1: Естественно, f₁₀. Вот один из вариантов – визуализация суммы 2 + 1 + 1 + 2 + 1 + 2 + 1.

То есть разрывы между плитками у нас будут после 2, 3, 4, 6, 7, 9 и 10 квадратов (попросту – везде, кроме центральной оси прямоугольников, в нашем примере – это после 1, 5 и 8 квадратов).

Ответ 2: Решим две задачи: сначала посчитаем варианты кладки, в которых будет разрыв после 5 квадрата (то есть ряд можно разделить пополам), потом те, где разрыва в этом месте не будет (и ряд будет разделяться на две неравные части). Начнем с первого. Левую часть можно выложить f₅ = 8 способами. Обе части равны, значит, и правую можно выложить f₅ = 8 способами. Согласно закону произведения (см. главу 4), мы можем представить общую сумму способов как f₅² = 8², как показано ниже:

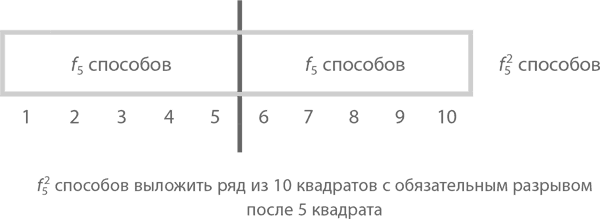
Теперь посчитаем те варианты, в которых разрыва в центре нет, зато мы точно знаем, что 5 и 6 квадраты закрыты прямоугольником (как нарисовано ниже). В таком случае части ряда как слева, так и справа от центрального прямоугольника можно выложить f₄ = 5 способами, значит, всего получается f₄² = 5². Сводим вместе оба варианта и получаем, что f₁₀ = f₅² + f₄², что и требовалось.

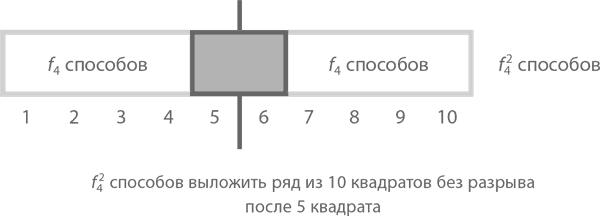
На уровне обобщений же трюк с разделением панелей длиной 2n квадратов на два типа в зависимости от того, есть ли у них по центру разрыв или нет, приводит нас к очень красивой закономерности –

А теперь рассмотрим другой пример. Что получится, если суммировать квадраты всех чисел Фибоначчи?

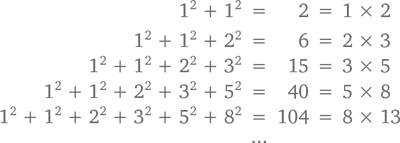
Ух ты! Здо́рово, правда? Сумма квадратов есть произведение двух последних чисел! Но зачем прибавлять сумму квадратов 1, 1, 2, 3, 5 и 8 к произведению 8 × 13? Лучший способ визуализировать это – взять шесть квадратов со сторонами 1, 1, 2, 3, 5 и 8 и расположить их так, как показано на схеме.

Берем один квадрат 1 на 1. Рядом с ним помещаем второй такой же. Получается прямоугольник 1 на 2. Под ним располагаем квадрат 2 на 2, и наш прямоугольник вырастает до 3 на 2. К его более длинной грани прибавляем квадрат 3 на 3 (получается прямоугольник 3 на 5); квадрат 5 на 5 отправляется вниз (получая прямоугольник 8 на 5), и, наконец, чертим самый большой квадрат, 8 на 8, тем самым заканчивая и прямоугольник 8 на 13. А теперь – простой вопрос.

Вопрос: Какова площадь большого прямоугольника?

Ответ 1: С одной стороны, это будет сумма площадей всех входящих в него квадратов, то есть 1² + 1² + 2² + 3² + 5² + 8².

Ответ 2: С другой стороны, высота большого прямоугольника равняется 8, длина же – 5 + 8 = 13, а значит, площадь – 8 × 13.

Так как оба эти ответа логически верны, они должны приводить нас к одному и тому же результату, который объяснит наше тождество. По большому счету, то, как мы строили этот прямоугольник, уже его объясняет – вместе со всеми отношениями между входящими в нее числами (я имею в виду 1² + 1² + 2² + 3² + 5² = 5 × 8). И если следовать этой логике и дальше, мы расширим наш прямоугольник сначала до 13 × 21, потом до 21 × 34 и т. д. до бесконечности. Общая формула выглядит так:

Посмотрим, что произойдет при перемножении двух соседних чисел последовательности Фибоначчи. «Соседями» 5, например, являются 3 и 8. Их произведение равно 3 × 8 = 24, что лишь на единицу меньше 5². «Соседи» 8 – 5 и 13, которые при умножении друг на друга дают 65 – число, которое на единицу больше 82. Таблица, показанная ниже, подтверждает эту закономерность: в последовательности Фибоначчи произведение двух соседних с искомым чисел будет всегда отличаться на 1 от квадрата этого искомого. Другими словами,

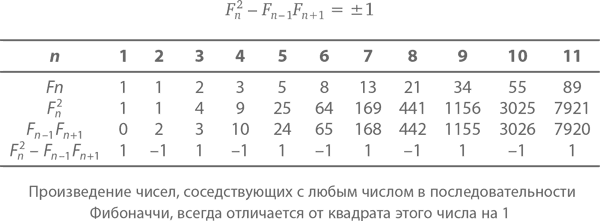
С помощью метода доказательства (называемого также индукцией), о котором мы подробно поговорим в следующей главе, приходим к тому, что при n ≥ 1

А почему бы нам не пойти дальше, к дальним соседям? Возьмем число F₅ = 5. Мы уже знаем, что его ближайшие «соседи» дают 3 × 8 = 24, что в шаге от 5². Но то же произойдет, если мы сделаем еще шаг влево и вправо по последовательности: 2 × 13 = 26, что так же в шаге от 5². А что насчет более отдаленных – на три, четыре шага – «соседей»? На пять, наконец? Получим 1 × 21 = 21, 1 × 34 = 34 и 0 × 55 = 0 соответственно. Насколько далеки эти результаты от 25? На 4, на 9 и на 25. Но это же квадраты натуральных чисел! Причем не всяких, а тех, что входят в последовательность Фибоначчи! Еще больше свидетельств этой закономерности – в таблице ниже, общая же формула выглядит так: