Книга: Опционы: Разработка, оптимизация и тестирование торговых стратегий
Назад: 4.2. Принципы формирования опционного портфеля
Дальше: 4.4. Одномерная система распределения капитала
4.3. Показатели, используемые для распределения капитала
4.3.1. Показатели, не связанные с оценкой доходности и риска
В разделе 4.2.1, описывая одномерную систему распределения капитала, мы вкратце охарактеризовали показатели, не связанные с оценками доходностей и рисков. Здесь мы продемонстрируем методику формирования портфеля по двум таким показателям и покажем, что один из них косвенно выражает величину риска.
Распределение капитала по эквиваленту позиции в акциях
Понятие «эквивалент» используется для соотнесения объема средств, которые потребуются в будущем (на дату истечения опционов) с размером опционной позиции по определенному базовому активу. Например, торговая стратегия может требовать, чтобы на дату экспирации в каждую акцию вкладывался равный объем капитала. Определим показатель «эквивалент позиции в акциях» как объем капитала, который потребуется в будущем (на дату экспирации либо на другую дату) при исполнении опционов, относящихся к определенному базовому активу.
Для формализации понятия «эквивалент» обозначим через C комбинацию, состоящую из разных опционов на один и тот же базовый актив. Предположим, что портфель формируется из m комбинаций (C1, C2… Cn). Пусть aj будет количеством комбинаций Cj, включенных в портфель. Если Uj – цена базового актива комбинации Cj, то для данной комбинации показатель эквивалента равен произведению aj Uj. Обозначим через M суммарный эквивалент портфеля (то есть объем капитала, который потребуется на дату истечения всех входящих в портфель опционов). При определении значений вектора a должно соблюдаться равенство:
a1U1 + a2U2 +… + amUm = M, (4.3.1)
означающее, что сумма эквивалентов всех комбинаций должна равняться суммарному эквиваленту портфеля.
Рассмотрим пример торговой стратегии, использующей такой способ распределения капитала, при котором показатель «эквивалент позиции в акциях» одинаков для всех комбинаций. Предположим, что M = $1 000 000 и что портфель формируется из 20 акций, входящих в S&P 500. Для каждой из них 28 августа 2010 г. были сгенерированы стрэддлы, состоящие из одного опциона колл и одного опциона пут с датой экспирации 17 сентября 2010 г. и страйками, ближайшими к текущим ценам акций. Котировки опционов брались на закрытие дня как полусумма цен спроса и предложения.
Равенство эквивалентов означает akUk = ajUj для каждой пары комбинаций i и j. Из приведенного выше равенства следует формула для всех j:

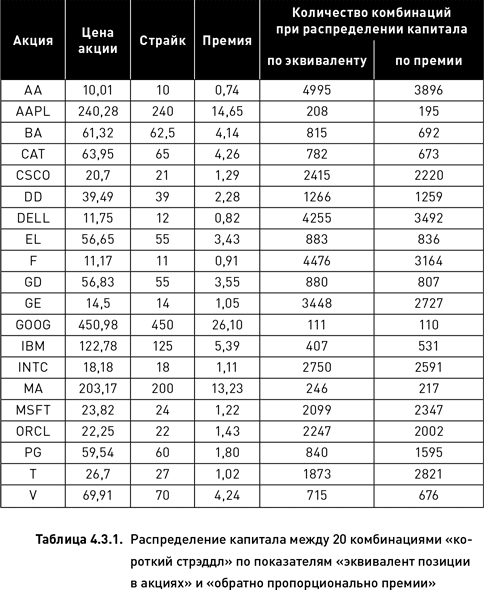
В таблице 4.3.1 приведено количество стрэддлов, получаемое при распределении капитала по равному эквиваленту. Эти количества рассчитаны таким образом, чтобы соблюдались два условия, необходимые для выполнения требований данной стратегии – равенство эквивалентов для всех акций и суммарный эквивалент портфеля $1 000 000. Например, для акции DELL, учитывая, что m = 20 и стоимость акции U7 = 11,75, число стрэддлов составляет a7 = 1 000 000/(20 × 1,75) = 4255,32. Мы для простоты округляем расчеты до двух цифр после запятой и не обращаем внимания на кратность лотов, принятую в реальной торговле.
Распределение капитала обратно пропорционально премии
Распределение капитала по премиям означает, что размер позиции по каждой комбинации определяется исходя из объема ее опционной премии. Рассмотрим в качестве примера торговую стратегию, основанную на таком принципе распределения капитала, который требует, чтобы суммарные премии, полученные от продажи всех экземпляров одной комбинации, были одинаковы. Это означает, что чем больше премия одной комбинации, тем меньше ее экземпляров будет включено в портфель. Поэтому такой подход называется «обратно пропорциональным».
Продемонстрируем данную методику распределения капитала на примере тех же комбинаций, что в предыдущем примере. Пусть pj – премия j-й комбинации, a aj – число ее экземпляров в портфеле. Равенство премий в портфеле aj pj = akpk означает, что числа (a1, a2… am) обратно пропорциональны абсолютным значениям премий отдельных комбинаций: 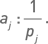 Формально количество экземпляров каждой комбинации в портфеле определяется по формуле
Формально количество экземпляров каждой комбинации в портфеле определяется по формуле
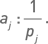 Формально количество экземпляров каждой комбинации в портфеле определяется по формуле
Формально количество экземпляров каждой комбинации в портфеле определяется по формуле

В нашем примере сумма отношений цен акций к премиям равна 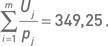 Премии комбинаций и соответствующие им значения aj приведены в таблице 4.3.1. Так, например, количество комбинаций для акции AAPL, премия стрэддла которой составляет p2 = $14,65, рассчитывается как:
Премии комбинаций и соответствующие им значения aj приведены в таблице 4.3.1. Так, например, количество комбинаций для акции AAPL, премия стрэддла которой составляет p2 = $14,65, рассчитывается как:
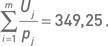 Премии комбинаций и соответствующие им значения aj приведены в таблице 4.3.1. Так, например, количество комбинаций для акции AAPL, премия стрэддла которой составляет p2 = $14,65, рассчитывается как:
Премии комбинаций и соответствующие им значения aj приведены в таблице 4.3.1. Так, например, количество комбинаций для акции AAPL, премия стрэддла которой составляет p2 = $14,65, рассчитывается как:

Сравнение двух принципов распределения капитала
Оба описанных нами способа распределения капитала по показателям, не связанным с оценкой доходности и риска, дали достаточно близкие результаты (таблица 4.3.1). Это объясняется тем, что чем дороже акция, тем меньшее количество опционов должно быть исполнено для получения заданного эквивалента. С другой стороны, абсолютная величина опционной премии обычно коррелирует с ценой акции и поэтому для более дорогих акций требуется продать меньше комбинаций для получения заданного объема премии.
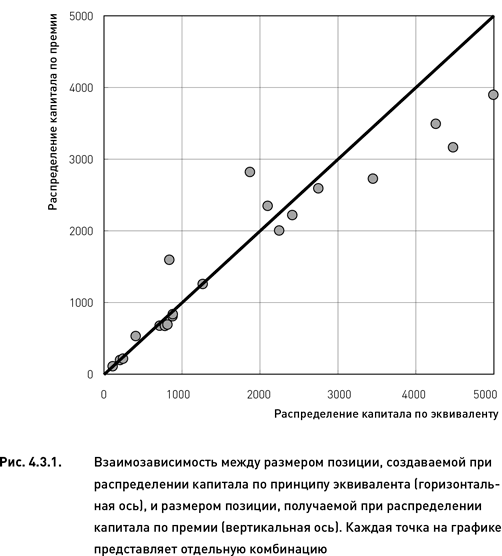
Вместе с тем, хотя количество комбинаций в портфелях, сформированных по двум рассмотренным принципам, довольно близко, оно не полностью идентично. Это хорошо видно на рис. 4.3.1, каждая точка на котором представляет одну из 20 комбинаций, входящих в состав портфеля. По горизонтальной оси отложен размер позиции, создаваемой при распределении капитала по принципу эквивалента; по вертикальной оси – размер позиции при распределении капитала по премии. Если бы результаты двух методов были одинаковы, то все точки-комбинации расположились бы вдоль показанной на рисунке наклонной линии. Однако мы наблюдаем достаточно большой разброс точек вдоль данной линии.
Причина дивергенции между двумя способами распределения капитала заключается в том, что корреляция между премией и ценой акции не абсолютна. Цена базового актива является далеко не единственным фактором, влияющим на стоимость опциона. Одним из основных факторов, определяющих стоимость опциона, является степень неопределенности относительно будущей цены базового актива (выражаемая обычно посредствам волатильности). Поэтому для двух акций, имеющих одинаковую стоимость (и совпадающих по другим параметрам), размер премии может быть разным. Следовательно, при прочих равных условиях комбинация с более высокой премией является более рискованной. Таким образом, получается, что более рискованные комбинации получают меньше капитала.
Эти рассуждения позволяют создать показатель, выражающий косвенным образом степень рискованности комбинации. Можно утверждать, что точки, расположенные ниже линии на рис. 4.3.1 соответствуют более рискованным комбинациям с более высокой премией. Количественно это можно выразить через отношение числа экземпляров комбинации, получаемого по формуле 4.3.2, к числу, получаемому по формуле 4.3.3. В результате получим показатель рискованности:
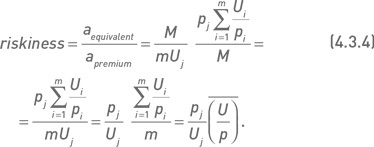
Из полученной формулы следует, что показатель рискованности равен произведению отношения премии j-й комбинации к цене j-й акции и среднего отношения цены базового актива к премии. Данный показатель обладает практичной размерностью – для более рискованных комбинаций (относительно всего портфеля) он больше единицы, а для менее рискованных комбинаций он меньше единицы. Если комбинация по своей рискованности приближается к средней рискованности портфеля, то этот показатель будет стремиться к единице. В приведенных выше примерах среднее отношение цены базового актива к премии составляет 17,5. Используя данные таблицы 4.3.1, можно показать, что для акции AAriskiness = (0,74 / 10,01) × 17,5 = 1,28, а для акции IBMriskiness = 0,77. Это означает, что комбинация, относящаяся к первой акции, более рискованна, чем комбинация, относящаяся ко второй.
Следует отметить, что показатель рискованности, рассчитываемый по формуле 4.3.4, может сам по себе использоваться для решения задачи распределения капитала, что позволит учитывать параллельно с премией и ценой акции еще и величину риска, ассоциированного с данной комбинацией. При этом необходимо оговориться, что данный показатель основывается на относительной дороговизне опционов, но не принимает в расчет степень ее обоснованность (с точки зрения исторической волатильности или ожидаемых новостей). Поэтому он не может претендовать на полное и всеобъемлющее выражение риска, а должен рассматриваться лишь как один из возможных инструментов решения задачи распределения капитала.
4.3.2. Показатели, выражающие оценку доходности и риска
Можно создать большое количество различных показателей, выражающих тем или иным образом оценку будущей доходности и прогноз рисков. Здесь мы ограничимся рассмотрением двух показателей доходности (математическое ожидание и вероятность прибыли) и трех показателей риска (дельта, коэффициент асимметрии и VaR).
В предыдущем разделе мы рассчитывали количество экземпляров каждой комбинации исходя непосредственно из параметров самой комбинации или ее базового актива. Применительно к показателям, оценивающим доходность и риск, предпочтителен (а во многих случаях и единственно возможен) более общий подход, основанный на распределении капитала с помощью набора весов. Для этого необходимо задать функцию j(С), вычисляемую для каждой комбинации C и принимающую неотрицательные действительные значения. Функцию φ(С) будем называть «весовой» функцией.
Весовая функция может применяться к двум типам показателей, которые мы будем условно называть «позитивными» и «негативными». Для позитивных показателей весовая функция φ(С) такова, что большие ее значения соответствуют более привлекательным комбинациям, а меньшие значения – менее привлекательным. К позитивным показателям относятся математическое ожидание и вероятность прибыли, а также все показатели, связанные с прогнозированием потенциала прибыльности. Для негативных показателей весовая функция φ(С) такова, что чем больше ее значение, тем менее привлекательна комбинация C. К негативным относится большинство показателей, оценивающих риск. Например, VaR, оценивающий размер убытка для заданной вероятности, принимает большие значения для более рискованных и, соответственно, менее привлекательных комбинаций.
Независимо от вида функции φ(С), вес j-й комбинации в составе портфеля определяется как:
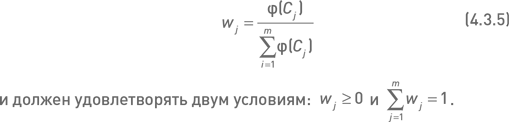
Способ вычисления количества экземпляров комбинации Cj в портфеле зависит от подхода, применяемого на первом уровне системы управления капитала. Если капитал, выделяемый для инвестирования в опционный портфель, представляет собой объем средств, который потребуется в будущем при исполнении опционов, то такой капитал является суммарным эквивалентом портфеля M (см. описание в предыдущем разделе). В этом случае количество экземпляров комбинации может быть рассчитано по формуле

или, что то же самое, но с помощью константы μ:
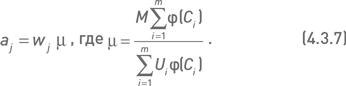
Если выделяемый для инвестирования капитал F представляет собой суммарный объем инвестиций в опционный портфель (например, суммарный объем маржевых требований по всему портфелю), то количество экземпляров комбинации Сj определяется по формуле
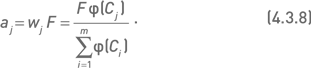
В дальнейших исследованиях мы будем использовать подход, основанный на суммарном эквиваленте портфеля (формула 4.3.7).
Математическое ожидание и вероятность прибыли
Эти два показателя, рассчитываемые на основе заданного распределения, представляют собой критерии оценки опционных комбинаций. Для простоты мы будем использовать логнормальное распределение. Математическое ожидание прибыли, рассчитанное на основе логнормального распределения, будем обозначать EPLN. Вероятность получения прибыли, рассчитанную на основе логнормального распределения, будем обозначать PPLN. Подробное описание и алгоритмы расчета этих показателей приводятся в нашей книге «Опционы: системный подход к инвестициям».
Оба показателя являются позитивными – большие значения показателей соответствуют более привлекательным комбинациям. Весовая функция φ(С) для j-й комбинации принимает значение показателя, соответствующее этой комбинации. В таблице 4.3.2 показаны значения критериев и соответствующие им значения весов, рассчитанные с помощью формулы 4.3.5. Примеры, приведенные в таблице, используют те же опционные комбинации, которые рассматривались в разделе 4.3.1.
Для расчета количества экземпляров каждой комбинации в составе портфеля необходимо воспользоваться формулой 4.3.7. Для примера вычислим вес и количество экземпляров комбинации, относящейся к акции CAT, для случая когда капитал распределяется по критерию «математическое ожидание прибыли». Из таблицы 4.3.2 следует, что Σφ(Ci) = 0,1196. Используя данные таблицы 4.3.1 для цен акций, можно рассчитать ΣUiφ(Ci) = 11,338. Принимая M = 1 000 000, получаем:
μ = 1000 000 × 0,1196: 11,338 = 10 550.
Учитывая, что для акции CAT φ(С4) = 0,001, вычисляем вес w4 = 0,001: 0,1196 = 0,0085 и число экземпляров комбинации. a4 = 10 550 × 0,0085 = 89,78. Используя этот же алгоритм расчета, легко показать, что при распределении капитала по критерию «вероятность прибыли» вес данной комбинации составит w4 = 0,472, а количество экземпляров a4 = 580,01.
Дельта, асимметрия и VaR
Дельта опциона выражает чувствительность цены опциона к изменениям стоимости базового актива. Для опционов, относящихся к одному базовому активу, дельта является аддитивной величиной. Поэтому дельта комбинации равна сумме дельт отдельных опционов. Дельта опциона колл принимает значения от 0 до 1, а дельта пута находится в диапазоне от −1 до 0. Соответственно, для одного стрэддла дельта может принимать значения от −1 до 1. Поскольку в наших примерах рассматриваются портфели, состоящие только из коротких стрэддлов, нейтральность комбинаций к поведению базового актива является в целом благоприятным фактором. Это означает, что чем ближе дельта комбинации к нулю, тем менее рискованной является позиция. Следовательно, при распределении капитала абсолютная величина дельты является «негативным» показателем. Поэтому мы зададим весовую функцию в следующем виде: φ(C) = 1 – |δ(C)|, где δ(C) – дельта комбинации C.
Коэффициент асимметрии является примером еще одного «негативного» показателя. Он представляет собой нормированную абсолютную разницу премии p опциона пут и премии c опциона колл, составляющих комбинацию C:
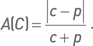
Идея данного показателя состоит в следующем. Торговые стратегии, основанные на коротких продажах опционных комбинаций, рассчитаны на то, что премия, полученная от продажи опционов, окажется больше, чем обязательства, возникающие в результате движения цены базового актива. Премия состоит из двух компонентов – временной и внутренней стоимости. Уже в момент открытия позиции внутренняя стоимость является будущим обязательством продавца опционов (исходя из нереалистичного, но на практике единственно возможного, допущения, что цена базового актива останется неизменной). Поэтому потенциал извлечения прибыли тем больше, чем меньше размер внутренней стоимости и чем больше величина временной стоимости. Это условие достигается при максимальном приближении страйка стрэддла к текущей цене базового актива. Чем более страйк удален от текущей цены, тем более асимметричной становится комбинация. Поскольку большие значения коэффициента асимметрии нежелательны для коротких стрэддлов, весовая функция будет иметь вид: φ(C) = 1 – A(C).
Value-At-Risk (VaR) представляет собой величину убытков, которые не будут превышены с заданной вероятностью (в наших примерах будем использовать вероятность 95 %). Для расчета VaR(C) сложных комбинаций и портфелей применяется метод моделирования Монте-Карло. Предполагая определенную форму распределения (в этом исследовании мы сделали допущение, что цена базового актива распределена логнормально, а дисперсия соответствующего нормального распределения доходностей равна квадрату исторической волатильности базового актива) производится моделирование траекторий будущих движений базового актива по торговым дням до момента экспирации. Подставляя полученные итоговые точки траекторий в платежную функцию комбинации, получаем смоделированное распределение ее значений на момент экспирации. Упорядочиваем его и отбрасываем 5 % худших значений. Среди оставшихся вариантов берем вариант с наименьшим значением платежной функции. Вычитая из него исходную премию комбинации, получаем оценку VaR(C) одной комбинации. Поскольку VaR выражает величину риска (комбинации с меньшим значением VaR предпочтительны), распределение капитала между ними логично производить обратно пропорционально этому показателю. Для распределения капитала между комбинациями обратно пропорционально их значениям VaR будем использовать весовую функцию φ(C) = 1: VaR(C).
В таблице 4.3.2 приведены значения весовых функций и соответствующих им весов для всех трех показателей риска. Кроме того, в этой таблице показаны значения коэффициента вариации весов (отношение стандартного отклонения к среднему) для каждой отдельно взятой акции и для каждого показателя. Среди акций наиболее высокий коэффициент вариации наблюдается для ORCL (0,93). Это означает, что среди всех 20 базовых активов объем капитала, инвестируемого в комбинацию ORCL, зависит в наибольшей степени от выбора показателя для распределения капитала. Действительно, из данных таблицы 4.3.2 следует, что если капитал распределяется по математическому ожиданию прибыли, то доля ORCL в общем портфеле составит менее 2 %. Если же для распределения капитала используется показатель VaR, то ORCL будет составлять 10 % портфеля. Наиболее низкий коэффициент вариации наблюдается для акции MSFT (0.17). Это означает, что среди всех базовых активов объем капитала, инвестируемого в MSFT, практически не зависит от выбора показателя. Какой бы показатель ни использовался для распределения капитала, доля MSFT в общем портфеле будет варьировать в очень узком диапазоне (от 5 до 7 %).
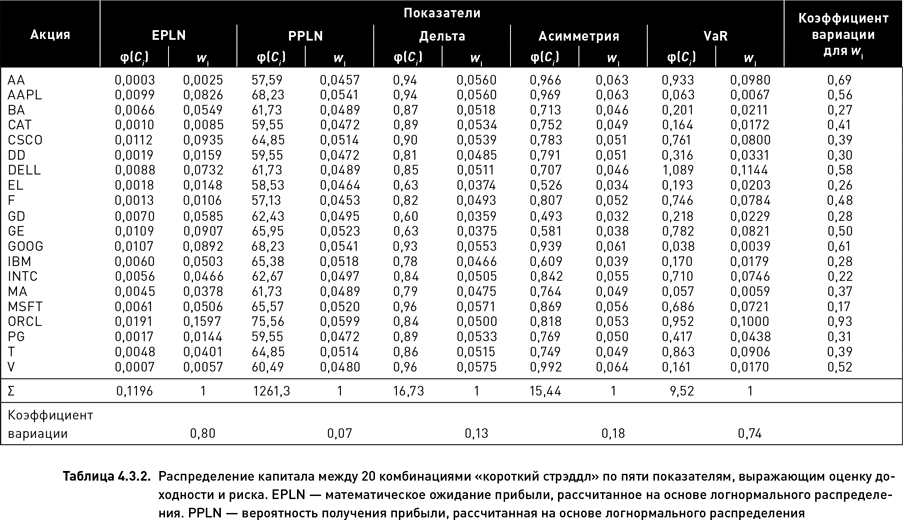
Сравнение коэффициентов вариации весов, рассчитанных для отдельных показателей, также дало интересные результаты. Наименее вариабельными оказались веса, полученные с помощью показателя «вероятность прибыли» (значение коэффициента 0,07, что на порядок ниже всех прочих). Это означает, что при использовании данного показателя, каждая акция получает примерно равную долю капитала. Следовательно, данный показатель мало применим для распределения капитала как минимум в тех условия и для той стратегии, что использовалась в наших примерах (это, однако, не означает, что он не может показать высокую эффективность при других обстоятельствах). На втором месте по вариабельности весов оказался показатель «математическое ожидание прибыли» (0,8), на третьем – дельта (0,13), на четвертом – коэффициент асимметрии (0,18), и самые вариабельные веса, причем с большим отрывом, были получены для показателя VaR (0,74). Примечательно то, что оба показателя, выражающие доходность, распределяют капитал внутри портфеля более равномерно (поскольку имеют более низкие значения коэффициента вариации), чем показатели, выражающие риск.
Назад: 4.2. Принципы формирования опционного портфеля
Дальше: 4.4. Одномерная система распределения капитала

