В предыдущем разделе мы использовали свойство робастности для выбора оптимального решения в пределах нескольких областей оптимизационного пространства. Говоря о понятии робастности, мы определили его как чувствительность целевой функции определенных узлов оптимизационного пространства к небольшим изменениям оптимизируемых параметров. Поскольку желательным свойством оптимального решения является большая робастность (то есть нечувствительность), то можно сказать, что, выбирая оптимальное решение, мы стремимся найти наиболее устойчивую оптимальную область. Подчеркнем, что в данном контексте речь идет об устойчивости по отношению к оптимизируемым параметрам.

В этом разделе будет рассмотрен другой аспект устойчивости – степень чувствительности оптимизационного пространства к неоптимизируемым параметрам. В процессе параметрической оптимизации, основанной на алгоритмическом вычислении целевой функции, исследуется множество комбинаций оптимизируемых параметров. При этом многие другие параметры остаются неизменным (будем называть такие параметры «фиксированными»). Их значения могут быть подобраны на более раннем этапе (используя научный подход) либо могут задаваться самой идеей и структурой стратегии, заложенной на начальном этапе ее формализации. Устойчивость оптимизационного пространства к небольшим изменениям фиксированных параметров и к незначительным изменениям в структуре стратегии является важным показателем надежности и качества оптимизации.

Поясним эту идею на простом примере. В процессе оптимизации базовой дельта-нейтральной стратегии нами была получена определенная оптимизационная поверхность (рис. 2.2.2). В этом случае оптимизировались только два параметра, значения всех остальных были зафиксированы. В частности, параметр «порог критерия» был зафиксирован на значении 1 % (позиции открывались только для тех опционных комбинаций, для которых ожидаемая прибыль была >1 %). Предположим, что мы увеличили значение данного параметра до 2 %. Далее предположим, что это привело к тому, что форма оптимизационной поверхности изменилась и стала выглядеть иначе (например, так, как показано на левом графике рис. 2.5.2). Если бы столь незначительное изменение фиксированного параметра привело к такому кардинальному изменению поверхности, то мы должны были бы заключить, что эта поверхность неустойчива, а сама оптимизация крайне ненадежна и, следовательно, полагаться на ее результаты весьма рискованно.

Рассмотрим устойчивость оптимизационного пространства базовой дельта-нейтральной стратегии по отношению к фиксированному параметру «порог критерия». На рис. 2.2.2 показана поверхность, полученная для целевой функции «прибыль» при условии, что порог критерия равен 1 %. Увеличим значение этого фиксированного параметра до 3 % и проверим, насколько такое изменение повлияет на форму оптимизационной поверхности.

Напомним, что до изменения фиксированного параметра глобальный максимум имел координаты 30 по параметру «число дней до экспирации» (горизонтальная ось графика) и 105 по параметру «период истории для расчета HV» (вертикальная ось). После увеличения значения фиксированного параметра глобальный максимум сместился и расположен в узле с координатами 16 и 120 соответственно. Учитывая общую площадь оптимизационного пространства, такое смещение глобального максимума нельзя назвать очень существенным (хотя оно безусловно не является пренебрежимо малым).

Исходное оптимизационное пространство имело единственную оптимальную область, протянувшуюся вдоль 30-й вертикали в диапазоне от 80 до 125 дней по параметру «период истории для расчета HV» (рис. 2.2.2). Левый график рис. 2.6.1 демонстрирует новое пространство, полученное в результате изменения фиксированного параметра. Прежняя оптимальная область сохранилась приблизительно на том же месте (незначительно сместившись вниз) и слегка увеличилась в размерах. Вместе с тем слева от оригинальной области появились четыре новые оптимальные области, две из которых очень маленькие, а две другие сопоставимы по размерам с прежней областью. Важно отметить, что, хотя количество оптимальных областей существенно выросло (пять вместо одной), все они располагаются приблизительно в левой нижней части оптимизационного пространства (12–36 дней по параметру «число дней до экспирации» и 40–180 по параметру «период истории для расчета HV»).

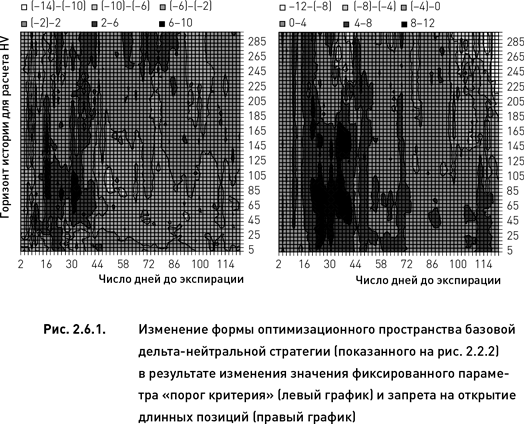
Из вышесказанного можно сделать вывод, что изменение фиксированного параметра не изменило принципиально форму оптимизационной поверхности. Это свидетельствует об относительной устойчивости оптимизационного пространства. Хотя произошедшие изменения могут показаться весьма существенными, необходимо принять во внимание, что изменение фиксированного параметра также было достаточно большим (с 1 % до 3 %). Мы специально использовали такое большое изменение, чтобы наглядно продемонстрировать видоизменение пространства. При тестировании устойчивости, производимой в ходе оптимизации автоматизированной стратегии, предназначенной для реальной торговли, можно ограничиться гораздо меньшими изменениями фиксированных параметров.

Понятие структурной устойчивости является очень широким. К структуре стратегии можно отнести практически все, начиная с базовой идеи и заканчивая относительно малозначительными техническими элементами. Изменение любого структурного элемента может коренным образом изменить форму оптимизационного пространства. Однако следует изначально ограничить область исследований структурной устойчивости. Интерес разработчика стратегии состоит в том, чтобы получаемое им оптимизационное пространство было устойчиво к небольшим изменениям структуры стратегии. Дело в том, что любое существенное изменение превращает оптимизируемую стратегию в совершенно другую стратегию, оптимизация которой, возможно, должна строиться совсем по-другому.

Примером небольших структурных изменений может быть метод распределения капитала или применение тех или иных инструментов управления рисками. Применительно к дельта-нейтральной стратегии, допустимое структурное изменение может заключаться, например, в изменении алгоритма расчета индексной дельты. С одной стороны, изменения этих и подобных им структурных элементов не меняет смысл стратегии. С другой стороны, желательно, чтобы оптимизационное пространство было устойчиво к изменениям такого рода. Например, если схема распределения капитала между элементами портфеля несколько изменяется и форма оптимизационного пространства не меняется коренным образом, то такая оптимизация является устойчивой и надежной. При этом следует помнить, что оптимизационное пространство может быть более устойчивым к одним структурным изменениям и менее устойчиво к другим.

В качестве примера рассмотрим промежуточный вариант структурного изменения – запрет на открытие длинных позиций. В принципе такое изменение является достаточно существенным и даже может полностью изменить смысл некоторых стратегий. Однако этот запрет может не быть абсолютным. Например, можно ввести мягкий запрет, ограничивающий долю длинных позиций в портфеле определенной пороговой величиной. Для того чтобы сделать изменение оптимизационного пространства визуально различимым, мы приведем пример полного запрета длинных позиций (хотя на практике такой жесткий тест на устойчивость вряд ли имеет смысл).

Правый график рис. 2.6.1 демонстрирует, что даже такое сильное изменение структуры стратегии, как полный запрет на использование длинных позиций, не изменило принципиально форму оптимизационной поверхности. Глобальный максимум сместился из узла с координатами 30 и 105 (по горизонтальной и вертикальной осям соответственно) в узле с координатами 30 и 70. Это означает, что оптимальное значение одного параметра не изменилось вовсе, а оптимум второго параметра несколько уменьшился.

Площадь прежней оптимальной области расширилась существенно. Кроме того, появилось несколько новых оптимальных областей. Это объясняется тем, что в течение последних 10 лет (период, на котором проводилась оптимизация), несмотря на недавний финансовый кризис, на рынке преобладали тенденции низко-волатильного умеренного роста. В таких условиях короткие опционные позиции более прибыльны по сравнению с длинными. Поэтому полный запрет на открытие длинных позиций привел к большему количеству прибыльных комбинаций параметров.

С точки зрения устойчивости важно то, что все оптимальные области группируются в одной части оптимизационного пространства, а именно вокруг оригинальной оптимальной области. Учитывая, что структурное изменение, заключающееся в полном запрете длинных позиций, является весьма существенным (на грани принципиального изменения стратегии), можно заключить, что устойчивость оптимизационного пространства в данном примере оказалась достаточно высокой.

В процессе параметрической оптимизации алгоритмическое вычисление целевой функции производится на основе исторических данных. Решение о длине исторического периода (называемого также «историческим горизонтом оптимизации») часто оказывает существенное влияние на результаты оптимизации. К сожалению, не существует объективных критериев выбора протяженности исторических временных рядов. Принято считать, что они должны включать в себя периоды с различной ценовой динамикой – кризисные периоды и периоды низковолатильного рынка. Также считается, что оптимизация должна проводиться на данных, включающих неблагоприятные периоды, а также периоды, благоприятствующие оптимизируемой стратегии. Придерживаясь этой концепции, некоторые создатели автоматизированных торговых систем предлагают использовать не сплошной (непрерывный) исторический ряд, а составлять базу данных из отдельных кусков истории, наиболее подходящих (по их мнению) для оптимизации определенной стратегии. Такой подход кажется нам неприемлемым, поскольку выбор «подходящих» отрезков исторических данных не может быть объективным.

По нашему мнению, для параметрической оптимизации следует использовать непрерывный ценовой (или какой-либо другой) ряд. Вопрос о длине этого ряда нужно решать исходя из идеи конкретной торговой стратегии. Однако, какой бы горизонт истории ни был бы выбран, необходимо стремиться к тому, чтобы результат оптимизации был устойчив к его изменениям. Чем менее оптимизационное пространство чувствительно к небольшим изменениям в протяженности периода оптимизации, тем надежнее и устойчивее будет создаваемая стратегия. Желательно, чтобы оптимизационное пространство было устойчивым даже при значительных изменениях в длине исторического периода. Идеальной может считаться ситуация, когда результаты оптимизации, проведенной на двухлетнем периоде, близки к результатам, получаемым на трехлетнем периоде, или когда результаты шести– и десятилетней оптимизации не слишком отличаются друг от друга.

Проведем тест на устойчивость оптимизационного пространства базовой дельта-нейтральной стратегии, оптимизируемой по целевой функции «прибыль». Для того чтобы определить степень устойчивости данного пространства к длине исторического периода, проведем последовательно серию оптимизаций на исторических периодах разной длины. Все оптимизации, представленные нами ранее в этой главе, основывались на десятилетнем историческом периоде. Теперь исследуем оптимизации, выполненные на девятом, восьмом, …, первом годах ценовой истории.

Для того чтобы результаты оптимизаций были сопоставимы (а также для того, чтобы было возможно построить свертку нескольких оптимизаций), необходимо чтобы значения целевой функции в каждом случае находились приблизительно в одном диапазоне. Это достигается с помощью трансформации, описанной в разделе, посвященном многокритериальному анализу (формула 2.4.1).

Сравнение 10 оптимизационных поверхностей (рис. 2.6.2, для простоты восприятия графиков показаны только оптимальные области) выявляет наличие двух устойчивых оптимальных областей, присутствующих почти на всех поверхностях. Одна из них расположена в районе 28–32 дней по параметру «количество дней до экспирации» и 85–140 дней по параметру «период истории для расчета HV» (будем условно называть эту область «левой»). Вторая оптимальная область имеет координаты 108–112 по первому параметру и 90–160 по второму (будем называть эту область «правой»).

Левая область присутствует на всех оптимизационных поверхностях, кроме двух– и трехлетней. Площадь ее поверхности достаточно стабильна (изменяясь весьма незначительно от случая к случаю). Исключение составляет только оптимизация, проведенная на однолетнем периоде. В этом случае левая область имеет большую площадь и, по сути, представляет собой три отдельные сгруппированные области.

Правая область также присутствует на всех оптимизационных поверхностях, за исключением единственного случая, когда оптимизация проводилась на десятилетнем периоде. Еще в двух случаях эта область оказалась несколько смещенной в область более высоких значений параметра «период истории для расчета HV». Площадь поверхности правой области более изменчива, чем площадь левой области. В оптимизациях, проведенных на 1-, 2-, 3-, 4– и 5-летнем периодах, правая область имеет довольно большие размеры. В противоположность этому на оптимизационных поверхностях, полученных на более продолжительных периодах, она имеет меньшую площадь поверхности. Кроме того, во всех случаях правая область не является единой, а раздроблена на большое количество субобластей.

Степень устойчивости оптимизационного пространства можно оценить разными методами. Самый простой из них – визуальный. Сравнение разных графиков рис. 2.6.2 в принципе указывает на то, что данная оптимизация достаточно устойчива. Это следует из описанного выше персистентного расположения оптимальных областей. Можно оценить степень устойчивости количественно, например, путем вычисления изменчивости координат узлов, составляющих оптимальные области.

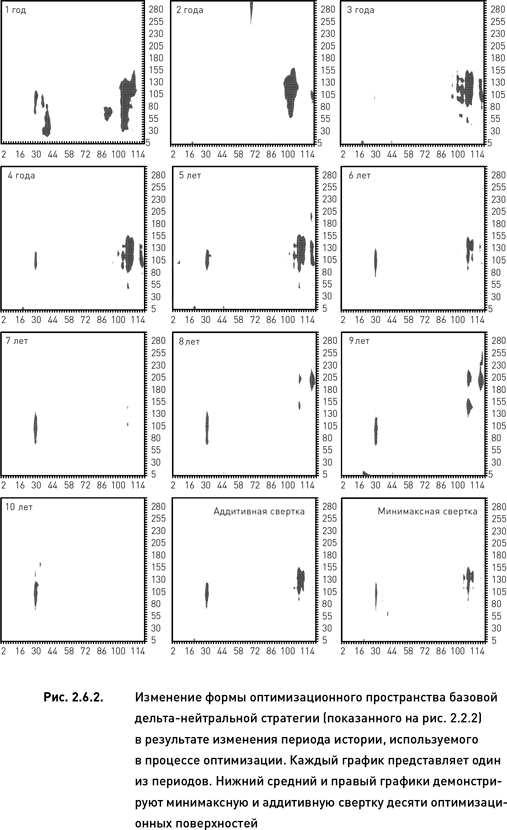
В том случае, когда устойчивость оценивается на основании сравнения большого количества оптимизационных поверхностей (как в нашем примере), можно использовать метод свертки. Идея заключается в том, что если поверхности очень отличаются друг от друга (то есть оптимизация является не устойчивой), то свертка таких поверхностей будет иметь большое количество беспорядочно разбросанных оптимальных областей. Если же оптимальные области располагаются на всех поверхностях приблизительно в одних и тех же местах (то есть если оптимизация устойчива), то свертка будет иметь одну или несколько четко обозначенных оптимальных областей. Нижний средний и правый графики рис. 2.6.2 демонстрируют аддитивную и минимаксную свертку десяти оптимизационных поверхностей (оба вида свертки оказались в данном случае почти идентичными). Левая и правая оптимальные области на этих свертках достаточно четко обозначены и локализованы, что еще раз подтверждает наш вывод об устойчивости оптимизации к изменению используемого периода истории.