До сих пор мы использовали самый информативный способ оптимизации – полный перебор всех возможных комбинаций параметров. Этот метод требует вычисления значений целевой функции во всех узлах оптимизационного пространства. Поскольку расчет целевой функции каждого узла требует сложных многоступенчатых вычислений, недостаток полного перебора состоит в большом количестве расчетов и времени требуемого для завершения полного оптимизационного цикла. С увеличением числа параметров количество расчетов и времени растет по степенному закону. Расширение области допустимых значений параметров и уменьшение шага оптимизации также увеличивают продолжительность времени, необходимого для полного перебора.

Во всех рассмотренных ранее примерах оптимизировались всего два параметра, для каждого из которых тестировались 60 значений. Соответственно, оптимизационное пространство состояло из 3600 ячеек. В среднем продолжительность одной прогонки (вычисление одного узла) составляла порядка одной минуты (при использовании системы параллельных вычислений на нескольких современных персональных компьютерах). Это означает, что для построения полного оптимизационного пространства, аналогичного рассматривавшимся ранее, требуется около 60 часов. Очевидно, что это неприемлемо для оперативной работы по построению и модификации автоматизированных торговых стратегий. Более того, добавление в систему лишь одного дополнительного параметра (всего три) увеличивает время вычислений до пяти месяцев! Все это делает полный перебор не самым практичным, а во многих случаях и вовсе не применимым, методом поиска оптимальных решений.

Решить эту проблему можно путем применения специализированных методик, не требующих полного перебора всех узлов оптимизационного пространства. Существует целая группа методов (от самых простых до невероятно сложных), позволяющих вести поиск максимума функции целенаправленно. Эта область прикладной математики продолжает быстро развиваться, постоянно разрабатываются новые, все более и более высокотехнологичные методики. В этом разделе мы не будем касаться двух самых популярных (из категории сложных) разделов оптимизации – генетических алгоритмов и нейронных сетей. Во-первых, эти методы настолько сложны, что каждый из них требует как минимум отдельной книги (количество публикаций на эту тему растет с каждым годом). Во-вторых, задачи параметрической оптимизации с ограниченным количеством параметров в большинстве случаев можно решить менее затратными способами (чрезвычайно сложные торговые системы, требующие применения этих методик, не являются предметом этой книги). В этом разделе мы рассмотрим пять специализированных методов поиска оптимальных решений. Эти методы были выбраны по принципу эффективности (с учетом специфики решаемых задач) и простоты их практической реализации.

Методы оптимизации, не требующие полного перебора, имеют два существенных недостатка. Предполагается, что оптимизационное пространство унимодально, то есть имеет единственный экстремум. При наличии в пространстве параметров нескольких локальных экстремумов (то есть когда пространство полимодально) эти методы могут привести к решению, которое не является наилучшим (то есть выбрать локальный экстремум вместо глобального максимума). Образно говоря, такую ситуацию можно описать как восхождение на вершину холма вместо покорения расположенного неподалеку горного пика. Это общий недостаток всех методов, использующих значения целевой функции в непосредственной близости от ранее вычисленных узлов, для постепенного улучшения значения функции. Это объективный недостаток, присущий всем без исключения методам целенаправленного поиска. Как мы уже сказали, гарантию нахождения глобального экстремума в общем случае дает лишь полный перебор всех узлов оптимизационного пространства.

Существует достаточно простой, хоть и затратный с точки зрения времени, способ решения этой проблемы. Если из содержательных соображений невозможно обосновать наличие в оптимизационном пространстве единственного экстремума, являющегося глобальным максимумом, следует многократно повторить процедуру «поиск экстремума при разных стартовых условиях» (то есть каждый раз начинать оптимизацию с разных узлов пространства). Стартовые узлы можно распределить равномерно в оптимизационном пространстве или выбрать случайным образом. Хотя достижение экстремума в этом случае не гарантируется, с практической точки зрения вероятность его получения может быть доведена до приемлемого уровня. Разумеется, чем больше попыток будет сделано, тем выше вероятность того, что хотя бы одна из них приведет к нахождению глобального максимума (однако и временные затраты также быстро возрастают). Чем больше оптимизационное пространство, тем больше попыток придется сделать.

Второй недостаток заключается в том, что найденное в результате целенаправленного поиска решение не несет в себе информацию о значениях целевой функции в узлах, соседствующих с узлом оптимального решения. Это означает, что мы не имеем возможности определить свойства оптимальной области, окружающей найденный экстремум. Следовательно, мы не в состоянии оценить степень робастности оптимального решения. Как обсуждалось в разделе 2.5, робастность является одним из основных показателей надежности оптимизации. Решить эту проблему можно только одним способом – вычислить значения целевой функции во всех узлах, окружающих найденные экстремумы. После этого можно оценить их робастность (используя одну из методик, описанных в разделе 2.5) и выбрать наилучший вариант в качестве оптимального решения.

Метод покоординатного подъема (обычно в названии этого метода используется слово «спуск», однако, как уже объяснялось ранее, для оптимизации торговых стратегий предпочтительно решать задачу максимизации прибыли) состоит в том, что последовательно производится поиск по каждому параметру, выбирая их один за другим по очереди. Алгоритм данного метода можно представить в следующем виде.

1. Выбирается стартовый узел, с которого начинается процесс оптимизации (выбор начальной точки требуется для инициации любого метода целенаправленного поиска). Выбор может быть случайным, осознанным (то есть основанным на предварительных знаниях разработчика) либо вычисленным (например, если будет производиться множество повторяющихся оптимизаций, то стартовые узлы могут распределяться в оптимизационном пространстве равномерно).

2. Поскольку параметры оптимизируются не одновременно, а последовательно, необходимо определить их очередность. В большинстве случаев очередность не имеет большого значения. Однако если какой-либо параметр более важен, чем другие, то начинать оптимизацию нужно именно с него.

3. Начиная со стартовой точки, находится наилучшее решение по первому параметру. Поиск его осуществляется каким-либо методом одномерной оптимизации. В большинстве случаев допустимо использовать полный перебор, поскольку количество вычисляемых узлов в этом случае относительно невелико. При исследовании первого параметра значения всех других параметров остаются зафиксированными на значениях стартового узла.

4. Переход к оптимизации по следующему параметру производится после того, как найдено наилучшее решение по первому. Вновь производится одномерная оптимизация, при этом значения всех других параметров остаются зафиксированными на значениях узла, найденного в ходе оптимизации первого параметра.

5. Закончив один оптимизационный цикл (заключающийся в одномерной оптимизации каждого из параметров), возобновляем процедуру, начиная с первого по списку параметра. Процесс останавливается после того, как очередной оптимизационный цикл не находит решение, превосходящее по значению целевой функции предыдущее.

Рассмотрим практическое применение данного алгоритма на примере оптимизации базовой дельта-нейтральной стратегии по целевой функции «прибыль» (оптимизационное пространство показано на рис. 2.2.2). Для того чтобы представить процедуру поиска оптимального решения визуально, ограничим области допустимых значений параметров диапазонами 2–80 для параметра «число дней до экспирации» и 100–300 для параметра «период истории для расчета HV». Выполнение алгоритма происходит следующим образом:

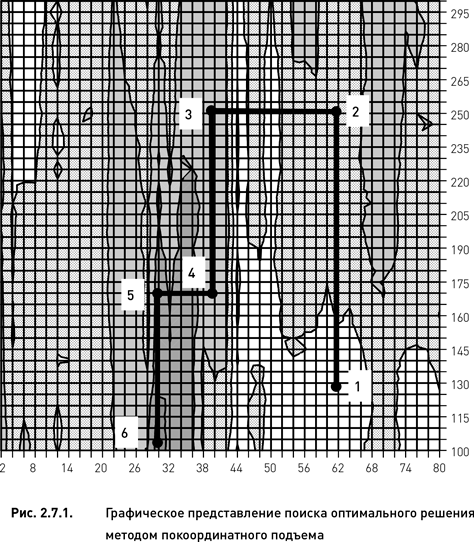
1. Выбираем стартовую точку. Предположим, что случайным образом был выбран узел с координатами 60 и 130. На рис. 2.7.1 данный узел отмечен номером 1.

2. Зафиксировав параметр «число дней до экспирации» на значении 60, вычисляем целевую функцию для всех значений параметра «период истории для расчета HV» (одномерная оптимизация методом полного перебора).

3. Определяем узел с максимальным значением целевой функции. В данном примере таким узлом является узел с координатами 30 и 250 (точка номер 2 на рис. 2.7.1).

4. Фиксируем значение параметра «период истории для расчета HV» на значении 250 и вычисляем целевую функцию для всех значений параметра «число дней до экспирации». Максимальное значение функции оказалось в узле с координатами 40 и 250 (третья точка).

5. Фиксируем число дней до экспирации на значении 40 и вычисляем целевую функцию для всех значений периода истории. Попадаем на следующий узел с координатами 40 и 170 (четвертая точка).

6. Фиксируем период истории на значении 170 и вычисляем целевую функцию для всех дней до экспирации. Попадаем на пятую точку с координатами 30 и 170.

7. Фиксируем число дней до экспирации на 30 и вычисляем целевую функцию для всех значений периода истории. Попадаем на шестую точку с координатами 30 и 105.

8. Фиксируем период истории на значении 105 и вычисляем целевую функцию для всех дней до экспирации. Выясняем, что максимум целевой функции приходится на исходный узел (точка номер 6). Это означает, что дальнейшего улучшения не происходит и, следовательно, алгоритм останавливается. Оптимальным решением является последний узел (номер 6).

Простой по своей логике и легко реализуемый, метод покоординатного подъема, однако, не очень эффективен. Представим себе ситуацию, когда двумерная оптимизационная поверхность имеет оптимальную область в форме узкого «горного хребта», протянувшегося с «северо-запада» на «юго-восток». Если высота хребта повышается в «юго-восточном» направлении, то, применив этот алгоритм, мы выйдем на гребень хребта и не сможем найти улучшения, поскольку для этого надо будет менять два параметра одновременно. Это сильно ограничивает применимость данного метода.

Этот метод был разработан с целью уменьшить вероятность возникновения ситуаций, в которых метод покоординатного подъема останавливается преждевременно, не найдя удовлетворительного оптимального решения. Он включает в себя последовательное применение двух процедур – исследующего поиска и поиска по образцу, повторяемых до нахождения неулучшаемого оптимума. По сравнению с методом покоординатного подъема применение метода Хука−Дживса существенно сокращает вероятность остановки алгоритма, не достигнув экстремума. Алгоритм метода Хука−Дживса имеет следующий вид.

1. Выбирается стартовый узел. Начиная с этого узла, выполняется процедура исследующего поиска. Данная процедура заключается в исполнении нескольких циклов описанного выше метода покоординатного подъема. Один цикл исследующего поиска состоит из n циклов покоординатного поиска (n – количество параметров). Для двумерного оптимизационного пространства требуется провести два цикла покоординатного подъема с тем, чтобы дополнительно к стартовому узлу найти два субоптимальных узла.

2. Выполняется процедура поиска по образцу. Для этого необходимо определить направление от стартового узла на найденный (в результате исполнения первого цикла исследующего поиска) узел. В этом направлении значение функции росло, и можно предположить, что, двигаясь далее в том же направлении, получим дальнейшее улучшение.

3. Выполняется процедура поиска в направлении, определенном на предыдущем этапе. В отличие от покоординатного подъема, данная оптимизация происходит при одновременном изменении всех параметров. Если в покоординатном подъеме движение возможно только по горизонтали или по вертикали (в двумерном случае), то поиск по образцу допускает движение вдоль любой прямой принадлежащей оптимизационной поверхности (или пространству в случае оптимизации более двух параметров).

4. Найдя наилучшую точку в этом направлении, повторяем цикл исследующего поиска, после чего вновь выполняем поиск по образцу, пока не достигнем точки, неулучшаемой ни на том, ни на другом этапе.

Рассмотрим применение метода Хука-Дживса на примере оптимизации базовой дельта-нейтральной стратегии по целевой функции «прибыль». По аналогии с предыдущим примером ограничим области допустимых значений параметров теми же диапазонами (2–80 для параметра «число дней до экспирации» и 100–300 для параметра «период истории для расчета HV»). Выполнение алгоритма происходит следующим образом:

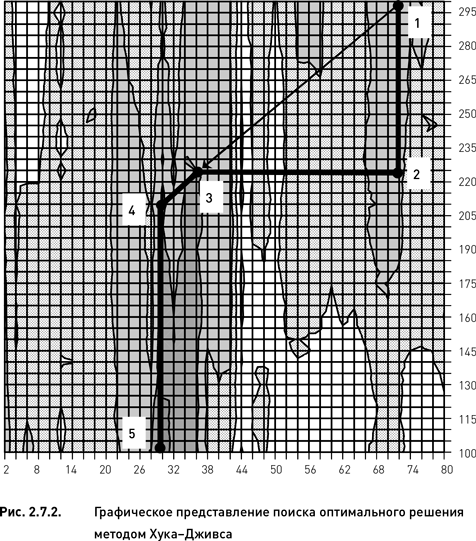
1. Случайным образом выбираем стартовую точку. Предположим, что был выбран узел с координатами 68 и 300. Данный узел отмечен номером 1 на рис. 2.7.2.

2. Начинаем процедуру исследующего поиска, заключающуюся в исполнении двух (по числу параметров) циклов покоординатного подъема. Зафиксировав параметр «число дней до экспирации» на значении 68, вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Определяем узел с максимальным значением целевой функции, каковым является узел с координатами 30 и 225 (точка номер 2 на рис. 2.7.2).

3. Фиксируем значение параметра «период истории для расчета HV» на значении 225 и вычисляем целевую функцию для всех значений параметра «число дней до экспирации». Максимальное значение функции приходится на узел с координатами 36 и 225 (третья точка).

4. Выполняем процедуру поиска по образцу. Определяем направление от стартового узла (номер 1) на узел 3 (стрелка на рис. 2.7.2) и выполняем одномерную оптимизацию в найденном направлении. Вычисляем значение целевой функции во всех узлах, пересекаемых диагональю в заданном направлении.

5. Выбираем узел с максимальным значением целевой функции (четвертая точка с координатами 30 и 210). Начиная с этого узла, повторяем цикл исследующего поиска.

6. Фиксируем значение параметра «число дней до экспирации» на значении 30 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Максимальное значение функции оказывается в узле с координатами 30 и 105 (пятая точка).

7. Фиксируем период истории на значении 105 и вычисляем целевую функцию для всех дней до экспирации. Выясняем, что дальнейшего улучшения не происходит и, следовательно, алгоритм останавливается. Оптимальным решением является узел номер 5.

Данный метод, называемый также методом вращающихся координат, является следующим шагом в усложнении метода покоординатного подъема. Первый его этап совпадает с методом покоординатного спуска. Затем, аналогично методу Хука и Дживса, находится направление, в котором улучшается целевая функция. Однако, помимо этого направления, строится еще (n − 1) направление, каждое из которых ортогонально найденному направлению и все они ортогональны между собой. Таким образом, вместо исходных параметров получается новая система координат. По отношению к исходной системе координат она повернута так, что одна из ее осей совпадает с направлением возрастания функции, найденном на предыдущем этапе. В этой системе координат производится очередной цикл покоординатного подъема, результат которого используется для нового вращения координат и следующего шага оптимизации. Для двумерного пространства алгоритм метода Розенброка имеет следующий вид.

1. Выбирается стартовый узел, начиная с которого выполняется цикл исследующего поиска (то есть два цикла покоординатного подъема).

2. Определяется направление от стартового узла на найденный узел и выполняется процедура поиска в этом направлении (поиск по образцу).

3. Найдя наилучший узел в этом направлении, строится направление перпендикулярное к ранее найденному направлению.

4. Производится поиск в перпендикулярном направлении и находится узел с наибольшим значением целевой функции.

5. Начиная с узла, найденного на перпендикулярном направлении, повторяем все процедуры (исследующий поиск, поиск по образцу, перпендикулярный поиск).

Рассмотрим практическое применение метода Розенброка на примере базовой дельта-нейтральной стратегии. Как и в предыдущих примерах, ограничим области допустимых значений параметров: 2–80 для параметра «число дней до экспирации» и 100–300 для параметра «период истории для расчета HV». Для выполнения алгоритма следует исполнить следующие процедуры:

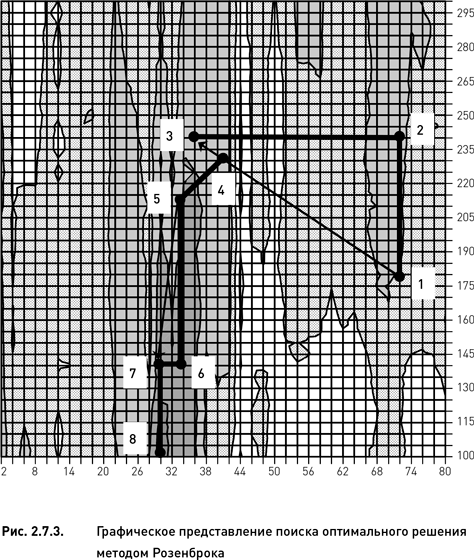
1. Случайным образом выбираем стартовую точку. Предположим, что был выбран узел с координатами 70 и 180. Данный узел отмечен номером 1 на рис. 2.7.3.

2. Начинаем процедуру исследующего поиска, заключающуюся в исполнении двух циклов покоординатного подъема. Фиксируем параметр «число дней до экспирации» на значении 70 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Узел с максимальным значением целевой функции имеет координаты 70 и 240 (точка номер 2 на рис. 2.7.3).

3. Зафиксировав параметр «период истории для расчета HV» на значении 240, вычисляем целевую функцию для всех значений параметра «число дней до экспирации». Максимум функции приходится на узел с координатами 36 и 240 (третья точка).

4. Выполняем процедуру поиска по образцу. Определяем направление от стартового узла (номер 1) на узел 3 (правая верхняя стрелка на рис. 2.7.3) и вычисляем значение целевой функции во всех узлах, пересекаемых данным направлением.

5. Находим узел с максимальным значением целевой функции (четвертая точка с координатами 40 и 230) и строим направление, перпендикулярное к ранее найденному направлению.

6. Производим поиск в новом (перпендикулярном) направлении и находим узел с наибольшим значением целевой функции (пятая точка с координатами 34 и 215).

7. Начиная с этого узла, повторяем цикл исследующего поиска методом покоординатного подъема. Фиксируем значение параметра «число дней до экспирации» на значении 34 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Максимальное значение функции оказалось в узле с координатами 34 и 140 (шестая точка).

8. Фиксируем период истории на значении 140 и вычисляем целевую функцию для всех дней до экспирации. Максимум функции приходится на узел с координатами 30 и 140 (седьмая точка).

9. Повторяем процедуру поиска по образцу. Определяем направление от пятой точки на седьмую точку (левая нижняя стрелка на рис. 2.7.3) и вычисляем значение целевой функции во всех узлах, пересекаемых данным направлением. Оказывается, что ни в одном из узлов указанного направления значение целевой функции не превосходит значение седьмой точки.

10. Строим направление, перпендикулярное направлению, указанному левой стрелкой (не показано на рисунке), и производим поиск вдоль этого направления. Оказывается, что и в этом направлении не находится ни одного узла, превосходящего по величине целевой функции седьмой узел.

11. Повторяем цикл исследующего поиска. Фиксируем значение параметра «число дней до экспирации» на значении 30 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Максимальное значение функции оказывается в узле с координатами 30 и 105 (восьмая точка).

12. Как мы уже видели в предыдущих примерах (метод Хука−Дживса), дальнейшего улучшения не происходит и, следовательно, алгоритм останавливается. Оптимальным решением является узел номер 8.

Метод Розенброка представляет собой усовершенствование методов покоординатного подъема и Хука−Дживса. В некоторых случаях он может заметно улучшить эффективность поиска, однако это происходит далеко не всегда. В определенных условиях, зависящих в основном от формы и структуры оптимизационного пространства, эффективность поиска может не только не повыситься, но даже снизиться.

Существуют две разновидности метода Нелдера – Мида (называемый также методом деформируемого многогранника, симплексным поиском, поиском методом амебы) – первоначальная, с использованием правильного симплекса, и усовершенствованная, с использованием деформируемого симплекса (в этом разделе мы рассмотрим усовершенствованную разновидность). Название отчасти может вводить в заблуждение, поскольку известен симплекс-метод линейного программирования, решающий задачу оптимизации с линейной целевой функцией при линейных ограничениях, с которым описываемый метод не имеет почти ничего общего. Под симплексом понимается многогранник в n-мерном пространстве, имеющий n + 1 вершину. Его можно рассматривать как обобщение треугольника на случай более чем двух измерений. Треугольник, в свою очередь, является примером симплекса в двумерном пространстве.

В процессе оптимизации симплекс, образно говоря, перекатывается в пространстве параметров, приближаясь к экстремуму. Вычислив значения целевой функции в его вершинах, находим худшее из них и перемещаем симплекс так, чтобы прочие вершины остались на месте, а взамен вершины с худшим значением была бы включена вершина, симметричная «худшей» относительно центра тяжести симплекса. Особенно наглядно это можно представить в двумерном случае, когда симплекс, а им в этом случае является треугольник, перекатывается через сторону треугольника, противолежащую к «худшей» вершине. Таким образом симплекс приближается к экстремуму, пока такие движения не перестанут улучшать целевую функцию. Наилучшая из полученных вершин является оптимальным решением. Однако у такого метода есть очевидный недостаток. Когда мы окажемся в непосредственной близости экстремума, так что расстояние от центра симплекса до экстремума станет меньше стороны симплекса, он потеряет способность приближаться к экстремуму. В этом случае можно уменьшить размер симплекса, при том, что он сохранит исходную форму, и продолжить поиск, повторяя это уменьшение размеров при потере способности приближаться к экстремуму, пока длина стороны не станет меньше шага оптимизации.

Метод деформируемого симплекса (деформируемого многогранника), помимо «перекатывания» его в пространстве параметров, включает и изменение его формы (что объясняет еще одно его название – «метод амебы»). Если у метода правильного симплекса нет иных параметров, кроме длины ребра симплекса, то здесь вводится система из четырех выбираемых исследователем параметров: коэффициент отражения α (обычно принимаемый равным 1), коэффициент растяжения σ (часто принимаемый равным 2), коэффициент сжатия γ (часто выбираемый равным 0,5), коэффициент редукции ρ (также может быть выбран 0,5). Как показывает опыт, выбор значений коэффициентов может оказаться критическим для получения удовлетворительных результатов оптимизации. Иногда рекомендуют выбирать коэффициенты γ и σ так, чтобы они не были взаимно обратными, например 2/3 и 2.

Алгоритм метода Нелдера – Мида состоит из следующих шагов:

1. Выбираются n + 1 точка начального симплекса x₁, x₂ … x_n+1. Это могут быть любые точки, не принадлежащие n-мерной гиперплоскости. В двумерном случае, когда симплекс является треугольником, достаточно, чтобы три точки не лежали на одной прямой.

2. Точки упорядочиваются согласно значениям целевой функции (при условии, что ставится задача максимизации функции):

3. Вычисляется точка x₀, являющаяся центром тяжести фигуры, вершины которой совпадают с точками симплекса, за исключением «худшей» точки x_{n + 1}:

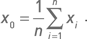
Для двумерной оптимизации x₀ располагается посредине отрезка, соединяющего лучшую и среднюю (по значениям целевой функции) точки треугольника.

4. Шаг отражения. Вычисляем отраженную точку:

Если значение целевой функции в отраженной точке лучше, чем во второй «худшей» точке x_n, но при этом не лучше, чем в наилучшей x₁, то отраженная точка заменяет в симплексе удаленную из него «худшую», и алгоритм возвращается на шаг 2 (симплекс «перекатился», уйдя от «худшей» точки в сторону увеличения целевой функции). Если значение целевой функции в «отраженной точке» лучше, чем во всех исходных точках, переходим к шагу 5.

5. Шаг растяжения. Производится вычисление «точки растяжения». Она находится на одном направлении с вектором, проведенным из «худшей» точки симплекса к центру тяжести, но дальше на величину, определяемую коэффициентом растяжения:

Содержательный смысл этой операции таков: если найдено направление, в котором целевая функция возрастает, симплекс растягивается в этом направлении. Если «точка растяжения» окажется лучше «отраженной точки», то последняя заменяется в симплексе «точкой растяжения», и он становится вытянутым в этом направлении. После этого возвращаемся в шаг 2. Если «точка растяжения» окажется не лучше «отраженной точки», то смысла в растяжении нет, в симплексе остается «отраженная точка», и форма его не меняется. Также следует возврат к шагу 2.

6. Шаг сжатия. На этот шаг мы попадаем, если отраженная точка не оказывается лучше хотя бы «второй худшей» точки. Производится вычисление «точки сжатия»:

Если полученная точка оказывается лучше «худшей» точки, то она заменяет ее в симплексе, и мы переходим в шаг 2. Симплекс при этом сожмется в этом направлении. Если же полученная точка окажется хуже и «худшей» точки, то это может свидетельствовать не о неудачном выборе направления, а о том, что мы уже находимся в непосредственной близости экстремума и для его нахождения необходимо уменьшить размер симплекса, чтобы не проскочить мимо него. Переходим к шагу 7.

7. Шаг редукции (reduction). Точка с наилучшим значением целевой функции остается на месте, а все остальные стягиваются к ней.

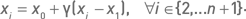
Если размер симплекса (ввиду его неправильной формы, нужно определить это понятие особо, например как максимальное расстояние от центра тяжести среди всех вершин) окажется меньше заданной величины, то алгоритм заканчивается. В противном случае переходим на шаг 2.

Рассмотрим практическое применение метода Нелдера – Мида для базовой дельта-нейтральной стратегии. Ограничим области допустимых значений параметров: 10–38 для параметра «число дней до экспирации» и 70–140 для параметра «период истории для расчета HV». Для выполнения алгоритма следует исполнить следующие процедуры:

1. Выбираем три точки начального симплекса. Предположим, что в качестве вершин симплекса были выбраны узлы с координатами 12 и 105, 18 и 110, 18 и 100.

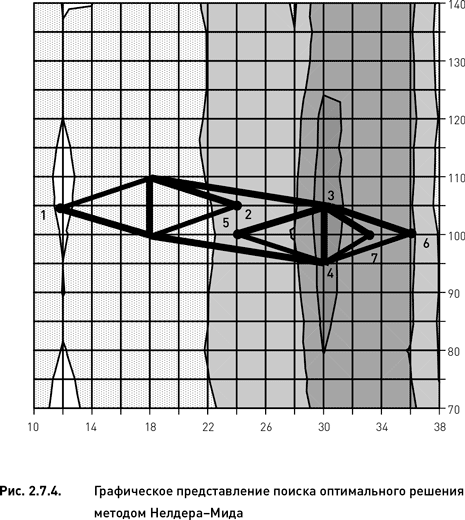
2. Находим худший (по значению целевой функции) узел начального симплекса. Данный узел отмечен номером 1 на рис. 2.7.4.

3. Вычисляем центр тяжести отрезка с координатами 18 и 110, 18 и 100. Центром является узел с координатами 18 и 105.

4. Выполняем шаг отражения, используя коэффициент растяжения α = 1. Отраженная точка, отмеченная номером 2 на рис. 2.7.4, имеет координаты 24 и 105. Поскольку значение целевой функции в отраженной точке лучше, чем во всех точках начального симплекса, переходим к шагу растяжения.

5. Вычисляем «точку растяжения», используя коэффициент растяжения σ = 2. Она находится путем удвоения расстояния между центром тяжести симплекса и второй точкой. Полученный узел (отмечен номером 3 на рис. 2.7.4) имеет более высокое значение целевой функции по сравнению с узлом номер 2 и поэтому заменяет последний, становясь новой вершиной симплекса.

6. Выполняем очередной шаг отражения. Отраженная точка отмечена номером 4 на рис. 2.7.4. Поскольку значение целевой функции в отраженной точке ниже, чем во второй худшей точке предыдущего симплекса, переходим к шагу сжатия.

7. Вычисляем «точку сжатия», используя коэффициент сжатия γ = 0,5. Получаем узел под номером 5. Поскольку этот узел лучше худшего в предыдущем симплексе, но не самый лучший, переходим к шагу отражения.

8. Выполняя шаг отражения, получаем узел номер 6. Поскольку значение целевой функции в этом узле ниже, чем во всех точках предыдущего симплекса, переходим к шагу сжатия.

9. Вычислив «точку сжатия», получаем точку номер 7. Поскольку данная точка попадает между двумя узлами, дальнейшее выполнение стандартного алгоритма Нелдера – Мида для данного оптимизационного пространства невозможно. Для выбора окончательного оптимального решения можно пойти несколькими путями. Можно вычислить целевую функцию точки 7 путем интерполяции как среднее арифметическое целевых функций узлов с координатами 32 и 100, 34 и 100. После чего можно продолжить исполнение стандартного алгоритма, вычисляя таким же образом все точки, не попадающие на узлы оптимизационного пространства. Другой, более простой, путь состоит в выборе оптимального решения среди одной из вершин последнего симплекса (той, которая имеет наибольшее значение целевой функции).

Этот алгоритм показал себя достаточно эффективным в решении задач разного рода и при этом достаточно прост в реализации. Осиновым его недостатком является большое количество параметров-коэффициентов, от выбора которых может сильно зависеть эффективность оптимизации. Как будет показано в следующем разделе, для эффективного использования метода Нелдера – Мида необходима тонкая настройка параметров и предварительная информация о свойствах оптимизационного пространства.

В предыдущем разделе мы описали четыре основных метода целенаправленного поиска оптимального решения. Каждый из них имеет свои особенности, достоинства и недостатки. Первый из рассмотренных методов (покоординатный подъем) является самым базовым и простым. Все прочие более сложны, причем каждый последующий является более сложным и, по идее, более совершенным, чем предыдущие (имеется в виду очередность их рассмотрения в разделе 2.7.1). Однако опыт показывает, что более сложные методы не всегда являются более эффективными. В общем виде можно утверждать, что эффективность того или иного метода зависит от формы оптимизационного пространства, на котором он применяется. Определенный метод может показать высокую эффективность на одном типе оптимизационного пространства, но оказаться непригодным для пространства, имеющего другую структуру.

В этом разделе мы исследуем эффективность четырех описанных ранее методов и протестируем зависимость их эффективности от формы оптимизационного пространства. Для этого мы применили каждый из методов поиска оптимального решения к двум разным по форме оптимизационным пространствам базовой дельта нейтральной стратегии. Одно из пространств имеет единственную оптимальную область относительно большого размера (оно формируется целевой функцией «прибыль», левый верхний график рис. 2.3.1), второе пространство имеет совершенно другую форму – множество небольших оптимальных областей (целевая функция «процент прибыльных сделок» левый нижний график рис. 2.3.1).

Чтобы получить статистически достоверные результаты, для каждой из двух целевых функций и для каждого метода было проведено по 300 полных оптимизационных циклов. Все циклы отличались друг от друга только стартовой точкой, с которой начинался поиск оптимального решения. Сравнительный анализ эффективности разных методов оптимизации базируется на следующих пяти показателях (в каждом случае они рассчитываются на основе 300 данных):

1. Процент оптимальных решений, совпадающих с глобальным максимумом (когда оптимизационный алгоритм остановился на узле с наибольшим значением целевой функции).

2. Процент оптимальных решений, расположенных в оптимальной области. Значения целевой функции этих решений не должны быть ниже определенного порогового значения.

3. Процент неудовлетворительных оптимальных решений. Целевые функции этих решений имеют значения, не превышающие определенную пороговую величину.

4. Среднее значение целевой функции всех оптимальных решений, рассчитанное на основе 300 полных оптимизационных циклов.

5. Среднее количество вычислений, необходимых для выполнения полного оптимизационного цикла.

В таблице 2.7.1 показаны значения всех пяти показателей эффективности для четырех методов целенаправленного поиска. Когда в качестве целевой функции использовалась прибыль, метод Хука−Дживса оказался наиболее эффективным. В 69 % случаев в качестве оптимального решения был выбран узел, соответствующий глобальному максимуму (соответственно, в 31 % случаев алгоритм поиска остановился, не найдя узел с самым высоким значением целевой функции). По проценту попаданий в оптимальную область (72 % от всех случаев) и по среднему значению целевой функции, рассчитанному для всех решений (6.43), данный метод также значительно превзошел все другие методы. Единственный показатель, по которому метод Хука−Дживса оказался несколько хуже (совсем ненамного) метода покоординатного подъема – это процент неудовлетворительных оптимальных решений (15 %). Однако существенным недостатком этого метода оказалась его затратность по времени. Для завершения одного полного оптимизационного цикла пришлось произвести в среднем 1279 вычислений. Это значительно больше, чем количество вычислений, требуемых для других методов.

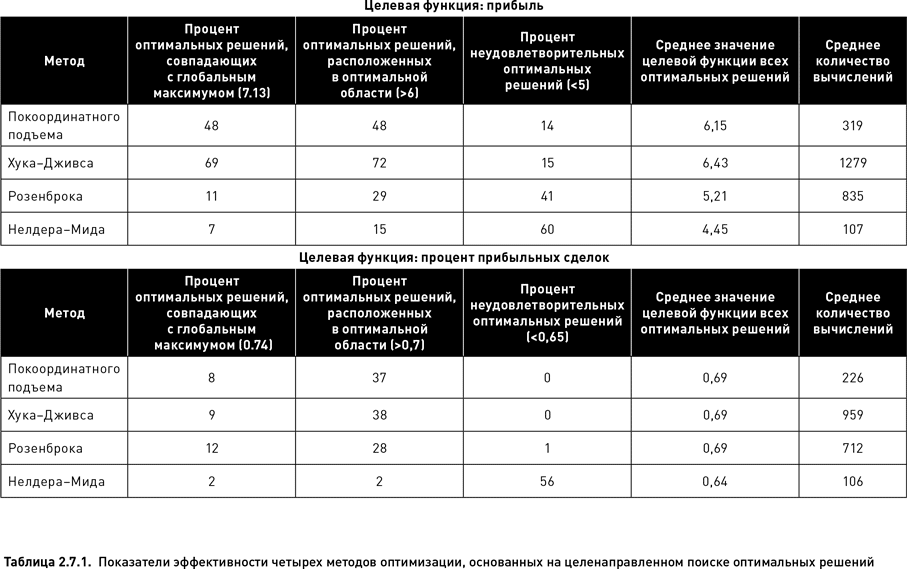
На втором месте по эффективности оптимизации унимодальной целевой функции (прибыль) находится метод покоординатного подъема. Хотя он несколько уступает по всем показателям (кроме процента неудовлетворительных оптимальных решений) методу Хука−Дживса, его несомненным достоинством является относительно небольшое количество требуемых вычислений (в среднем 319, что в четыре раза меньше, чем требуется при использовании метода Хука−Дживса).

Метод Розенброка существенно уступает по эффективности двум предыдущим методикам. Лишь в 11 % случаев с помощью этого метода удалось обнаружить узел глобального максимума, а в 41 % случаев алгоритм остановился на ячейках, относящихся к областям с низкими значениями целевой функции. Кроме того, количество вычислений, требуемых для нахождения оптимальных решений, по методу Розенброка оказалось достаточно большим (в среднем 835), находясь на втором месте после метода Хука−Дживса.

Наихудшие результаты были получены для метода Нелдера – Мида. Хотя количество вычислений для этого метода оказалось наименьшим по сравнению с другими методами, все показатели его эффективности находятся на очень низком уровне. Всего в 7 % случаев решение совпало с глобальным максимумом и лишь в 15 % случаев оптимальное решение находилось в оптимальной области. В 60 % случаев решения оказались неудовлетворительными.

Для другого оптимизационного пространства, построенного на основе целевой функции «процент прибыльных сделок», эффективность методов покоординатного подъема Хука−Дживса и Розенброка оказалась приблизительно одинаковой (если не считать того, что последний метод был несколько хуже по показателю «процент попаданий в оптимальную область»). Метод Нелдера – Мида вновь показал наихудшие результаты. Такая низкая эффективность данного метода весьма удивительна. Возможно, она объясняется тем, что для успешного применения этого метода необходимо тщательно подбирать стартовые условия (размер симплекса), а также значения его многочисленных параметров (коэффициенты отражения, сжатия, редукции, расширения). Мы же выбрали размер симплекса произвольно, а для коэффициентов приняли обычно используемые значения. Вероятно, для получения удовлетворительных результатов необходима более тонкая настройка параметров и некоторые априорные предположения о свойствах оптимизационного пространства.

Для оптимизационного пространства, соответствующего целевой функции «процент прибыльных сделок», эффективность всех четырех методов оптимизации оказалась значительно ниже по сравнению с их эффективностью на пространстве функции «прибыль». Это подтверждает наше предположение о том, что форма оптимизационного пространства оказывает значительное влияние на эффективность оптимизации. По всей видимости, унимодальные пространства с относительно широкой оптимальной зоной легче поддаются оптимизации методами целенаправленного поиска, чем полимодальные пространства с большим количеством раздробленных оптимальных областей.

До сих пор мы рассматривали два подхода к оптимизации – полный перебор, требующий вычисления целевой функции во всех узлах оптимизационного пространства, и целенаправленный поиск. Возможен еще один подход, состоящий в вычислении целевой функции в случайно выбранных узлах оптимизационного пространства. Безусловно, случайный поиск представляет собой самый простой способ оптимизации. Для его реализации достаточно выбрать случайным образом заданное количество узлов и рассчитать значения целевой функции для каждого из них. После этого узел с наибольшим значением выбирается в качестве оптимального решения. Этот метод настолько примитивен, что зачастую вообще не рассматривается в качестве приемлемой методики. Тем не менее во многих случаях (и по многим показателям) случайный поиск может дать достаточно эффективные результаты, не уступающие методам целенаправленного поиска.

Основной и единственный фактор, влияющий на эффективность случайного поиска, – это количество выбираемых ячеек. Чем больше делается попыток, тем выше вероятность того, что оптимальное решение совпадет с глобальным максимумом или будет лежать в непосредственной близости от него. При этом количество попыток должно определяться в зависимости от размеров оптимизационного пространства. В наших примерах это пространство состоит из 3600 ячеек. Если для случайного поиска в таком пространстве использовать 100 попыток, то обследованными окажутся менее 3 % ячеек, что, очевидно, недостаточно для нахождения удовлетворительного оптимального решения. Однако если оптимизационное пространство состоит из 500 ячеек, то 100 попыток составят 20 %, что может оказаться достаточным.

В этом разделе мы проанализируем три аспекта эффективности случайного поиска:

1. Зависимость эффективности поиска от количества случайно выбираемых узлов. Эффективность будет тестироваться для 100, 200, …, 1000 попыток (всего 10 вариантов количества выбираемых узлов).

2. Влияние формы оптимизационного пространства на эффективность случайного поиска. Как и в предыдущем разделе, мы применим метод случайного поиска к оптимизационным пространствам, соответствующим целевым функциям «прибыль» и «процент прибыльных сделок».

3. Сравнение эффективности случайного поиска с двумя методами целенаправленного поиска – покоординатным спуском и методом Хука−Дживса (которые оказались наиболее эффективными среди других методов целенаправленного поиска).

Для анализа эффективности случайного поиска воспользуемся теми же показателями, которые использовались для сравнения четырех методов целенаправленного поиска (таблица 2.7.1).

Как и следовало ожидать, значения всех показателей растут по мере увеличения количества случайно выбранных узлов (рис. 2.7.5 и 2.7.6). Однако темпы этого роста зависят от каждого конкретного показателя. Более того, форма зависимости эффективности поиска от количества попыток различна для разных показателей. Процент оптимальных решений, совпадающих с глобальным максимумом, увеличивается линейно с ростом количества проверенных узлов. С другой стороны, процент оптимальных решений, расположенных в оптимальной области, и среднее значение целевой функции всех оптимальных решений растут нелинейно по мере увеличения количества попыток: в начале рост происходит быстрыми темпами, затем дальнейшее увеличение числа попыток приводит лишь к незначительному росту эффективности поиска.

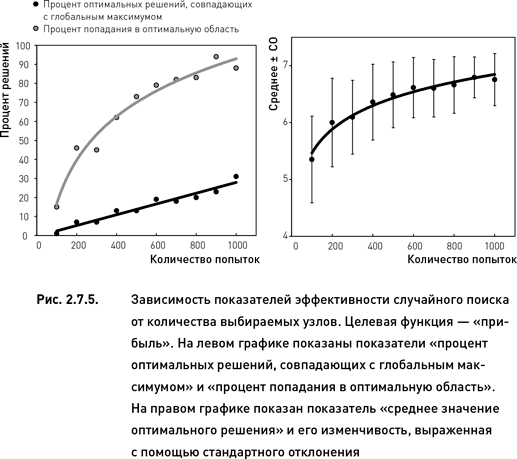
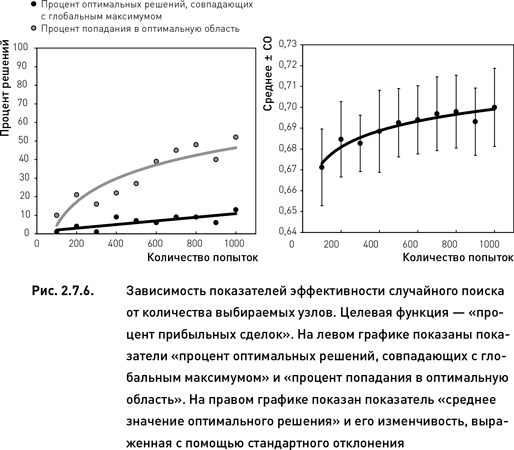
Эффективность случайного поиска выше для оптимизационного пространства, соответствующего целевой функции «прибыль» по сравнению с пространством «процент прибыльных сделок» (сравни левые графики рис. 2.7.5 и 2.7.6). Это полностью совпадает с результатами целенаправленного поиска, полученными в предыдущем разделе. Кроме того, для целевой функции «прибыль» изменчивость показателя «среднее значение оптимального решения» уменьшается при увеличении числа попыток (правый график рис. 2.7.5). В то же время для целевой функции «процент прибыльных торговых циклов» такая зависимость не наблюдается (правый график рис. 2.7.6).

По показателю «процент оптимальных решений, совпадающих с глобальным максимумом» случайный поиск уступает покоординатному подъему и методу Хука−Дживса. Однако при использовании достаточного количества попыток случайный поиск оказывается более эффективным по двум другим показателям. Для целевой функции «прибыль» случайный поиск становится эффективнее покоординатного подъема по показателям «среднее значение оптимального решения» и «процент попадания в оптимальную область» начиная с 400 попыток. При использовании 500 попыток данный метод превосходит и вторую методику, Хука−Дживса (сравни рис. 2.7.5 с данными таблицы 2.7.1). Для целевой функции «процент прибыльных сделок» случайный поиск становится эффективнее покоординатного подъема и метода Хука−Дживса по проценту попаданий в оптимальную область начиная с 600 попыток. По среднему значению оптимального решения случайный поиск превосходит эти две методики начиная с 700 попыток (сравни рис. 2.7.6 с данными таблицы 1).

Проведенный анализ приводит к ряду полезных выводов относительно применимости случайного поиска для оптимизации торговых стратегий. В общем виде можно утверждать, что при увеличении числа попыток до определенного уровня, вероятность того, что наилучшее из полученных решений окажется достаточно близким к глобальному максимуму, может быть удовлетворительно велика. В частности, случайный поиск может использоваться, если (1) размеры оптимизационного пространства позволяют исследовать порядка 20 % его ячеек и (2) имеется предварительная информация об унимодальности оптимизационного пространства. Последнее возможно в тех случаях, когда в процессе построения стратегии уже производилась оптимизация путем полного перебора, в ходе которой форма пространства была установлена. Если пространство оказывается близким по форме к тому, которое было получено нами для целевой функции «прибыль» (рис. 2.2.2), то при дальнейших доработках и модификациях стратегии можно использовать метод случайного поиска.