В предыдущем разделе мы рассмотрели вопрос выбора целевых функций для их дальнейшего использования в системе многокритериальной оптимизации. Данный раздел посвящен поиску оптимальных решений с помощью методов многокритериального анализа. Применительно к параметрической оптимизации задача многокритериального анализа состоит в одновременном использовании многих целевых функций (каждая из которых представляет собой отдельный критерий) для упорядочения узлов оптимизационного пространства (каждый из которых представляет собой определенную уникальную комбинацию параметров) по степени их предпочтительности.

Основная проблема многокритериальной оптимизации состоит в том, что полное упорядочение альтернатив может оказаться невозможным по причине их нетранзитивности. Поясним это на простом примере. Будем считать лучшим тот вариант, который превосходит остальные по большинству критериев. Предположим, что при сравнении трех узлов (А, В и С) по значениям трех целевых функций (критериев) был получен следующий результат: A = (1; 2; 3), B = (2; 3; 1), C = (3; 1; 2) – в скобках указаны значения критериев. Очевидно, что по первому и второму критерию узел B предпочтителен узлу A, а C лучше B по первому и третьему критерию. При соблюдении свойства транзитивности из этого должно следовать, что узел C предпочтителен A. Однако это не так, поскольку A превосходит C по двум критериям, второму и третьему.

Проблема нетранзитивности не имеет универсального решения. Тем не менее существуют два основных подхода, позволяющих получить приемлемое оптимальное решение (или несколько решений), несмотря на несоблюдение свойства транзитивности. Первый подход основывается на приведении всех целевых функций к единому критерию, называемому «свертка», второй подход состоит в применении метода Парето.

Отказ от одновременного использования нескольких критериев путем замены их новым единственным критерием (представляющим собой некую функцию, аргументами которой являются исходные критерии) составляет суть свертки. Преимуществом свертки является простота реализации и возможность регулировать степень влияния различных критериев на результат оптимизации. Это достигается путем умножения значений критериев на выбранные весовые коэффициенты – чем больше вес данного критерия, тем большее влияние он окажет на окончательный результат многокритериальной оптимизации. Основным недостатком свертки является неизбежная потеря информации при переходе от многомерного вектора критериев к единственному показателю.

Наиболее распространенными являются два вида свертки: аддитивная (сумма или среднее арифметическое значений всех критериев) и мультипликативная (произведение или среднее геометрическое значений всех критериев). Применение мультипликативной свертки возможно, только если критерии неотрицательны (поскольку произведение двух отрицательных значений дают положительную величину), либо если только один из критериев может принимать отрицательные значения. Также нужно учитывать, что если один из критериев равен нулю, то и мультипликативная свертка равна нулю (для аддитивной свертки этого не происходит). В мультипликативной свертке по сравнению с аддитивной большее влияние оказывают критерии, имеющие более низкие значения. Аддитивная свертка наиболее приемлема для критериев, представляющих собой однородные по смыслу и близкие по масштабу значений величины.

Кроме аддитивной и мультипликативной, существует также селективная свертка, когда для каждого узла принимается в качестве значения свертки наименьшее (наиболее консервативный вариант свертки) или наибольшее (наиболее агрессивный вариант) значение из всего набора целевых функций. В книге «Опционы: системный подход к инвестициям» мы предложили методику минимаксной свертки, когда в качестве значения свертки используется произведение наибольшего и наименьшего значений критериев.

При расчете свертки необходимо помнить о том, что критерии могут измеряться в разных единицах и иметь различный масштаб величин. Для приведения их к единой шкале с одинаковыми диапазонами значений можно воспользоваться следующей трансформацией:

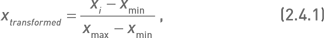
где x_i – значение критерия для i-го узла x, x_min и x_max – минимальное и максимальное значение критерия соответственно. Применение этой формулы позволяет привести значение критерия к интервалу от 0 до 1.

Продемонстрируем применение свертки на примере базовой дельта-нейтральной стратегии. В качестве критериев выберем три из четырех целевых функций, показанных на рис. 2.3.1 – прибыль, максимальную просадку и процент прибыльных сделок (коэффициент Шарпа не будет использоваться в силу его сильной скоррелированности с прибылью). Применив формулу 2.4.1, мы привели значения всех трех целевых функций к интервалу от 0 до 1. Построив три варианта свертки (аддитивную, мультипликативную и минимаксную), мы убедились в том, что в данном случае все они дают весьма близкие результаты.

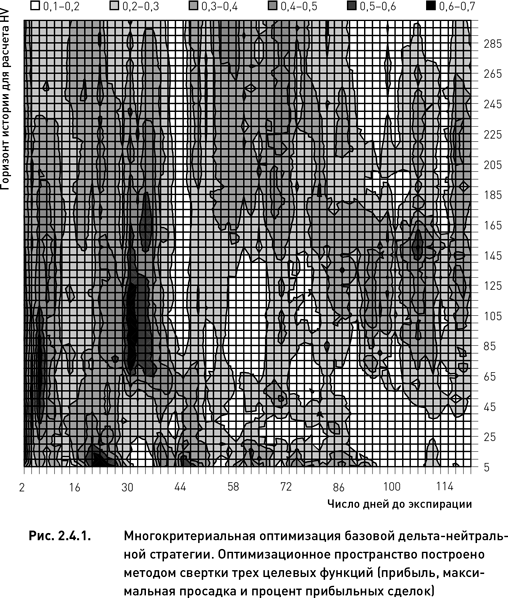
На рис. 2.4.1 показана оптимизационная поверхность минимаксной свертки. Данная поверхность полимодальна и имеет четыре оптимальные области. Три из них имеют относительно обширную площадь, а одна очень мала (поскольку площадь поверхности является одним из важных факторов при выборе оптимального решения, четвертую область можно не рассматривать). Как видим, многокритериальный анализ методом свертки не позволил в данном случае получить единственное оптимальное решение, так как каждая из зон содержит свое оптимальное решение. Следовательно, само по себе построение свертки не решило до конца задачу оптимизации. Необходимо выбрать из трех зон одну. Поскольку все они обладают приблизительно одинаковыми высотными отметками (значение свертки), то выбор должен осуществляться по другому принципу. В следующем разделе мы рассмотрим вопрос выбора оптимальной области на основании характеристик рельефа и количественных оценок робастности потенциальных оптимальных решений.

Применение метода Парето позволяет решить задачу выбора в условиях, когда показатели различных критериев противоречат друг другу. Подобная ситуация, когда некоторые узлы оптимизационного пространства превосходят другие узлы по одной из целевых функций (например, по прибыли), но являются хуже их по другой функции (например, по максимальной просадке), возникает довольно часто. Основным недостатком метода Парето является то, что в результате оптимизации может быть получено множество оптимальных решений вместо одного. Это потребует дальнейшего анализа, и выбор придется делать на основе применения дополнительных методик. Такая же проблема свойственна и методу свертки, но в гораздо меньшей степени.

Формализация задачи многокритериальной оптимизации выглядит следующим образом. Пусть для каждого узла (альтернативы) a из оптимизационного пространства задан n-мерный вектор значений целевых функций (критериев) x(a) = (x₁(a), …, x_n(a)). Используя показатели n критериев, необходимо найти альтернативы с максимальными значениями координат векторов (то есть с максимальными показателями целевых функций). Будем считать, что чем больше значение критерия, тем лучше альтернатива. При сравнении двух альтернатив a и b альтернатива a доминирует над альтернативой b, если выполняется следующая совокупность неравенств: x_i(a) ≥ x_i(b), для всех значений i = 1, …, n, и существует хотя бы один критерий j, для которого выполняется строгое неравенство x_j(a) > x_j(b). Другими словами, узел a предпочтителен узлу b, если a не уступает b по значениям всех целевых функций и хотя бы по одной из них превосходит b.

Очевидно, что наличие доминирования однозначно определяет, какая из двух сравниваемых альтернатив лучше. Если же отношение доминирования установить невозможно, то вопрос о том, какая из них лучше, остается открытым. В этом случае говорят, что ни одна из альтернатив не обладает однозначным превосходством (не доминирует) над другой.

Используя приведенные рассуждения, задачу многокритериальной оптимизации можно сформулировать следующим образом: среди множества всех альтернатив найти такое подмножество, в которое входят только недоминируемые альтернативы, то есть те, для которых не существует доминирующих их альтернатив. Это подмножество и называется множеством Парето. Каждый элемент такого множества можно считать наилучшим в определенном выше смысле. При этом число альтернатив, составляющих это множество, может быть самым различным. Например, это может быть как одна, доминирующая над всеми остальными, альтернатива, так и несколько «лучших» альтернатив или даже все исходное множество.

В нашем примере оптимизации базовой дельта-нейтральной стратегии мы имеем оптимизационное пространство A = (a₁, …, a_m), состоящее из m узлов-альтернатив (в примере m = 3600), оцененных с помощью n функций-критериев (n = 3) со значениями x(a) = (x₁(a₁), …, x_n(a_m)). Для построения множества Парето необходимо попарно сравнить все альтернативы, отбрасывая доминируемые, а недоминируемые добавляя в множество Парето. Очередной элемент ak сравнивается со всеми оставшимися. Если встречается элемент a_l, над которым a_k доминирует, то элемент a_l отбрасывается. Если оказывается, что a_k доминируем каким-либо элементом a_m из оставшихся, то отбрасывается элемент a_k. Если ни один из элементов не доминирует над a_k, то последний включается во множество Парето. Далее переходим к сравнениям элемента, следующего за a_k, со всеми оставшимися элементами. При этом максимальное количество требуемых сравнений составляет порядка 0,5m (m – 1), что вполне приемлемо для большинства случаев. Более быстрые алгоритмы требуются при построении множества Парето для большого числа критериев и альтернатив.

Как было сказано выше, недостатком метода Парето является невозможность повлиять на количество узлов, попадающих в оптимальное множество Парето. Число элементов множества может изменяться от случая к случаю и не зависит от наших пожеланий и предпочтений. Единственное оптимальное решение может быть получено только в том случае, когда оптимизационное пространство имеет узел, для которого показатели всех критериев превосходят соответствующие показатели для других узлов. В большинстве случаев вместо единственного оптимального решения получается множество.

Рассмотрим применение метода Парето на примере базовой дельта-нейтральной стратегии. В качестве критериев будем использовать те же три целевые функций, что использовались в многокритериальной оптимизации методом свертки (прибыль, максимальная просадка и процент прибыльных сделок). В отличие от свертки, метод Парето не позволяет построить полное оптимизационное пространство, аналогичное поверхности, показанной на рис. 2.4.1. Вместо этого мы получаем перечень доминирующих узлов, составляющих оптимальное множество. В результате оптимизационная поверхность превращается в координатную плоскость, обозначающую положение отдельных оптимальных узлов (рис. 2.4.2).

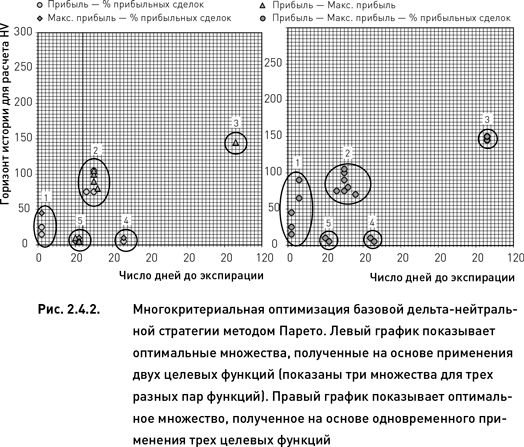
Двигаясь от простого к более сложному, рассмотрим сначала оптимальное множество Парето, полученное путем применения двух критериев. Из трех целевых функций можно составить три пары критериев, что позволяет получить три варианта оптимального множества. Узлы, попавшие в эти оптимальные множества, группируются на координатной плоскости в пяти областях. На левом графике рис. 2.4.2 эти области обозначены условными порядковыми номерами. Интересно отметить, что ни в одну из пяти областей не попали все три варианта оптимального множества. В третью область попал единственный узел множества, полученного в результате применения целевых функций «прибыль» и «максимальная просадка». Узлы, выбранные этой парой функций, попали также во вторую и пятую области. Узлы, соответствующие паре функций «прибыль» и «процент прибыльных сделок», расположены в первой, второй и четвертой областях. И, наконец, узлы, попавшие в оптимальное множество функций «максимальная просадка» и «процент прибыльных сделок», находятся в областях 1, 4 и 5. Такое распределение оптимальных множеств по областям координатной плоскости свидетельствует о том, что каждая из трех целевых функций вносит свой вклад в поиск оптимального решения. Поэтому в данном случае имеет смысл включить все три функции в систему многокритериальной оптимизации по методу Парето.

Множество оптимальных решений, полученное в результате применения трех критериев показано на правом графике рис. 2.4.2. Узлы, попавшие в оптимальное множество Парето, расположены на координатной плоскости приблизительно в тех же пяти областях, что и в предыдущем примере, когда для оптимизации использовались пары критериев. Наибольшее количество узлов (всего семь) попало во вторую область, в первой области оказалось пять узлов, а в третьей, четвертой и пятой областях – всего по два узла.

Следует отметить, что в предыдущем примере, когда использовалось только по два критерия, оптимальные множества состояли из пяти – семи элементов (в зависимости от пары критериев). Использование трех критериев привело к расширению множества до 18 элементов. Это является общим свойством метода Парето – увеличение количества решений. Поскольку задача параметрической оптимизации требует выбора единственного оптимального узла, то включение в оптимизационную схему каждой дополнительной функции полезности усложняет решение этой задачи. Поэтому, принимая решение о выборе тех или иных целевых функций, следует принимать во внимание не только объем новой информации, вносимой в общую систему каждой дополнительной функцией, но и учитывать сложность выбора единственного оптимального решения из большого количества вариантов.

Расположение оптимальных областей, полученных по методу свертки, достаточно близко к расположению аналогичных областей, полученных по методу Парето (сравни рис. 2.4.1 и 2.4.2). Это означает, что применение обеих методик в данном случае приводит к одному и тому же результату (при этом следует учитывать, что в других случаях результаты могут быть разными, и тогда придется делать выбор между двумя методами).

Основной результат многокритериальной оптимизации, продемонстрированной в этом разделе, состоит в том, что обе методики позволили определить несколько оптимальных областей. Однако ни одна из них не привела к выбору единственного оптимального решения. Следовательно, можно сказать, что задача оптимизации решена не до конца. Необходимо в пределах выбранных областей продолжить поиск единственного оптимального решения. Этому вопросу посвящен следующий раздел.