С помощью целевой функции мы оцениваем и сравниваем между собой меру полезности различных комбинаций параметров. Поэтому выбор целевой функции является одним из ключевых элементов, во многом определяющим эффективность оптимизации. Каждая функция создает оптимизационное пространство, имеющее свои характерные особенности. Оптимизационные пространства разных функций полезности могут быть достаточно близкими по своей форме, а могут существенно отличаться друг от друга. В этой главе мы рассмотрим различные функции полезности, создающие как похожие, так и весьма далекие по форме пространства.

В большинстве случаев невозможно ограничиться одной функцией полезности. Обычно приходиться использовать не менее трех-четырех функций одновременно. Иногда их количество бывает гораздо большим (до 10 и даже более). Использование большого количества целевых функций особенно актуально для оптимизации опционных торговых стратегий, поскольку в этом случае приходится оценивать не только стандартные параметры доходности и риска, но также особые характеристики, специфичные для опционов. В главе 1 мы рассматривали множество таких функций, когда говорили о характеристиках опционных портфелей. Увеличение количества целевых функций приводит к необходимости разработки специальных методик многокритериального анализа. Значительная часть материала текущей главы будет посвящена этому непростому вопросу.

При оптимизации большинства автоматизированных торговых систем основной целевой функцией является прибыль (этот показатель может иметь разные формы выражения – в процентах или абсолютных цифрах, в годовом эквиваленте или с привязкой к операционному циклу системы). Все примеры, рассмотренные нами ранее в этой главе, основывались именно на этой целевой функции. Левый верхний график рис. 2.3.1 воспроизводит оптимизационное пространство, построенное на основании этой базовой функции. Теперь мы рассмотрим, насколько выбор других целевых функций влияет на форму оптимизационной поверхности тех же параметров.

При использовании в качестве целевой функции коэффициента Шарпа (правый верхний график рис. 2.3.1) форма поверхности выглядит почти так же, как и для функции «прибыль» (за исключением мелких, незначительных расхождений). Наибольшая по площади оптимальная область располагается приблизительно в одном и том же месте и имеет похожую форму. Глобальный максимум имеет почти те же координаты, что и для целевой функции «прибыль». Единственное отличие состоит в том, что координата по вертикальной оси составляет 100 дней для функции «коэффициент Шарпа» вместо 105 дней для прибыли (это незначительное отличие вряд ли имеет какое-либо принципиальное значение). Следует также отметить, что данная оптимизационная поверхность полимодальна, поскольку имеет еще несколько оптимальных областей, содержащих локальные максимумы. Однако в силу того, что эти области очень невелики по площади, с точки зрения робастности они явно уступают области глобального максимума.

Следующая функция полезности, максимальная просадка – представляет собой общепризнанный показатель риска торговых стратегий. Оптимизационное пространство, соответствующее этой функции, показано на правом нижнем графике рис. 2.3.1. В отличие от других показателей оптимизация максимальной просадки требует нахождения минимума, а не максимума функции полезности. Поэтому оптимальными являются те области поверхности, которые имеют низкие высотные отметки. В отличие от коэффициента Шарпа оптимизационное пространство данного показателя полностью отличается от пространства, соответствующего целевой функции «прибыль». Оптимальные области располагаются в двух направлениях: (1) в первой половине диапазона значений параметра «количество дней до экспирации» при условии, что параметр «горизонт истории для расчета IV» имеет низкие значения (вдоль горизонтальной оси); (2) в широком диапазоне значений параметра «горизонт истории для расчета IV» при условии, что параметр «количество дней до экспирации» имеет низкие значения (вдоль вертикальной оси). В этих же местах были отмечены оптимальные зоны (хоть и значительно меньших размеров) для функции «коэффициента Шарпа». Это объясняется тем, что коэффициент Шарпа «содержит в себе» информацию о риске (стандартное отклонение в знаменателе формулы). Поскольку максимальная просадка является экстремальным «выбросом» доходностей, то она влияет самым непосредственным образом на стандартное отклонение и опосредовано на коэффициент Шарпа.

Показатель «процент прибыльных сделок» также является общепризнанной мерой прибыльности системной торговли. При использовании этого показателя в качестве целевой функции (левый нижний график рис. 2.3.1) получается оптимизационная поверхность принципиально отличная по форме от поверхностей других функций. Во-первых, вместо единственной оптимальной области (полученной для функции «прибыль») или нескольких таких областей (полученных для функций «коэффициент Шарпа» и «максимальная просадка») поверхность функции «процент прибыльных сделок» имеет множество оптимальных областей (она в большой степени полимодальна). Во-вторых, все оптимальные области данной функции представляют собой небольшие островки, в то время как большинство оптимальных областей других целевых функций имеют относительно большие площади поверхности. И, в-третьих, что самое главное, оптимальные области функций «прибыль» и «коэффициент Шарпа» не совпадают с оптимальными областями функции «процент прибыльных сделок».

Изучив оптимизационные пространства четырех функций полезности, мы можем сделать несколько важных выводов. Каждая из функций несет определенный объем информации, часть которой дублируется информацией, содержащейся в других функциях, а часть является уникальной, неповторяющейся информацией. При этом степень совпадения информации может быть разной для разных функций. Например, коэффициент Шарпа не добавляет почти никакой новой информации к информации, содержащейся в функции «прибыль». Поэтому вряд ли будет целесообразным использовать обе этих функции одновременно (объем дополнительных вычислений не оправдывает ту малую долю дополнительной информации, которая может быть получена). В то же время другие функции полезности содержат значительный объем новой недублирующей информации, которая не может быть получена с помощью функции «прибыль». Поэтому включение таких функций в систему многокритериальной оптимизации может быть вполне оправданным.

В этом разделе мы провели визуальный сравнительный анализ различных функций полезности и отметили разную степень дублирования содержащейся в них информации. Для того чтобы придать этим умозрительным заключениям количественное выражение, которое может быть использовано для окончательного выбора целевых функций, необходимо изучить их корреляции. Этому посвящен следующий раздел.

Для того чтобы выразить количественно степень дублирования информации, содержащейся в различных функциях полезности, следует сравнить попарно взаимозависимости этих функций. Чем меньше корреляция между функциями, тем меньше пересечение информации и тем это лучше с точки зрения многокритериальной оптимизации. Коэффициент корреляции выражает степень взаимозависимости функций, а коэффициент детерминации (квадрат коэффициента корреляции) выражает долю изменчивости одной функции полезности, которая объясняется изменчивостью второй функции. Следовательно, показатель, равный разности единицы и коэффициента детерминации, позволяет оценить долю дополнительной, недублирующей информации, которая попадает в систему оптимизации в результате введения в нее дополнительной функции полезности.

Корреляционный анализ показал, что все целевые функции взаимозависимы в большей или меньшей степени (рис. 2.3.2). Как и следовало ожидать, наибольшая корреляция существует между прибылью и коэффициентом Шарпа (внешняя схожесть оптимизационных пространств этих двух функций отмечалась нами в предыдущем разделе). В этом случае коэффициент корреляции очень высок (r = 0,95). Следовательно, доля недублирующейся информации, составляет всего 10 % (1 – 0,952 = 0,10). Поэтому не имеет смысла использовать одновременно и прибыль, и коэффициент Шарпа в рамках одной оптимизационной схемы.

Степень взаимозависимости между прибылью и процентом прибыльных сделок, а также между прибылью и максимальной просадкой гораздо ниже, чем между прибылью и коэффициентом Шарпа (обратная зависимость в случае с максимальной просадкой, по сути, является прямой, поскольку низкие значения просадки являются предпочтительными). В первом случае коэффициент корреляции равен 0,37 (левый средний график рис. 2.3.2), а во втором – 0,35 (правый верхний график рис. 2.3.2). Это означает, что доля недублирующейся информации для этих пар целевых функций составляет 86 и 88 % соответственно. Эти значения достаточно высоки для того, чтобы серьезно рассматривать вопрос о целесообразности их включения в систему многокритериальной оптимизации. Однако, принимая такое решение, необходимо определить, имеет ли смысл использовать обе эти функции или достаточно одной из них.

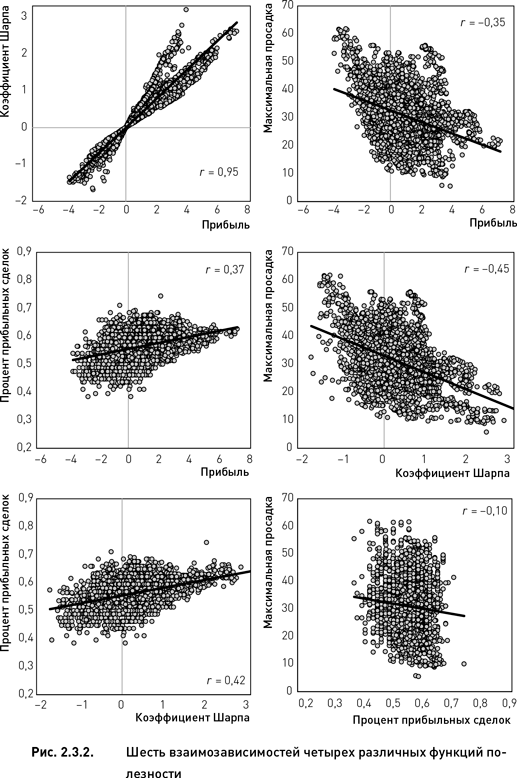
Для того чтобы принять такое решение, необходимо изучить взаимозависимость между этими двумя функциями полезности. Как следует из правого нижнего графика рис. 2.3.2 и низкого коэффициента корреляции (0,10), значения процента прибыльных сделок и максимальной просадки практически не зависят друг от друга. Информация, содержащаяся в этих двух функциях, почти не повторяется (доля не дублируемой информации составляет 99 %). Следовательно, добавление обеих целевых функций в систему многокритериального анализа вполне оправдано.

Таким образом, из четырех рассмотренных нами целевых функций имеет смысл использовать для многокритериальной оптимизации только три (прибыль, процент прибыльных сделок и максимальную просадку). Исключение из многокритериального анализа коэффициента Шарпа оправдывается не только тем, что эта функция почти полностью дублирует функцию прибыли, но еще и тем, что коэффициент Шарпа коррелирует с процентом прибыльных сделок и с максимальной просадкой в гораздо большей степени, чем функция прибыли (средний правый и левый нижний графики рис. 2.3.2).

Описанная выше процедура выбора целевых функций выглядит достаточно просто. Однако необходимо признать, что мы сознательно упростили эту процедуру, для того чтобы излишне не усложнять описание. Теперь мы устраним это упрощение, чтобы продемонстрировать всю сложность и многоплановость процесса выбора подходящих целевых функций.

Дело в том, что взаимозависимости, представленные на рис. 2.3.2, были построены на основании всего набора данных, составляющих оптимизационные пространства целевых функций. Это значит, что данные взаимозависимости строились для полных диапазонов значений двух параметров (2–120 дней для количества дней до экспирации опционов, 5–300 дней для периода истории для расчета HV). Например, для оценки корреляции между прибылью и коэффициентом Шарпа каждому узлу на левом верхнем графике рис. 2.3.1 ставилась в соответствие точка на правом верхнем графике. Полученная в результате такого сопоставления зависимость (верхний левый график рис. 2.3.2) состоит из 3600 точек.

Вместе с тем вполне можно предположить, что степень, и даже направленность, взаимозависимостей между разными целевыми функциями может меняться в зависимости от конкретных значений параметров и, соответственно, от диапазонов их значений. Для того чтобы проверить это предположение, следует рассчитать корреляции для каждого из значений двух параметров по отдельности (то есть нужно проверить, меняются ли корреляции в зависимости от значений параметров).

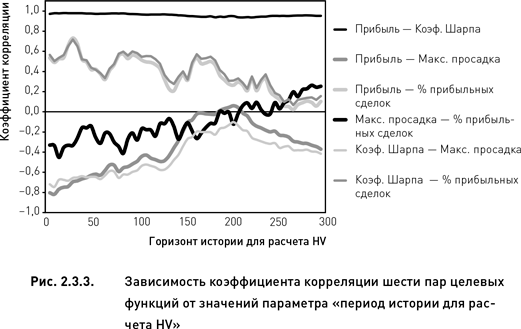
Начнем с параметра «период истории для расчета HV». Корреляции между некоторыми парами целевых функций зависят, а между некоторыми – не зависят от значений этого параметра (рис. 2.3.3). Например, корреляция функций, для которых была отмечена наибольшая степень взаимозависимости (прибыль и коэффициент Шарпа), не меняется на всем диапазоне значений параметра. Все прочие пары функций демонстрируют явно выраженные тренды.

Взаимозависимость пары целевых функций «прибыль» и «процент прибыльных сделок» достаточно высока при низких значениях параметра «период истории для расчета HV». По мере увеличения значений параметра степень скоррелированности двух этих функций снижается и падает до нуля, когда параметр достигает верхней границы диапазона своих допустимых значений. Такой же точно тренд характеризует и взаимозависимость другой пары целевых функций «коэффициент Шарпа» и «процент прибыльных сделок». Такая схожесть трендов не удивительна, принимая во внимание почти абсолютную скоррелированность значений прибыли и коэффициента Шарпа.

Две другие пары целевых функций (прибыль и максимальная просадка, коэффициент Шарпа и максимальная просадка) также демонстрируют почти одинаковый тренд (причина схожести трендов та же, что и в предыдущем случае). Корреляции для этих двух пар при низких значениях параметра достаточно сильны (напомним, что в случае максимальной просадки отрицательный коэффициент корреляции имеет тот же смысл, что и положительная корреляция). По мере увеличения параметра до средних значений корреляция приближается к нулю, а затем вновь уходит в отрицательную область. Когда мы рассматривали те же данные консолидированно (правый верхний и правый средний графики рис. 2.3.2), то могли обнаружить только обратную зависимость для этих пар целевых функций. Детализированный анализ, представленный на рис. 2.3.3, позволяет установить, что в диапазоне средних значений параметра «период истории для расчета HV» корреляции внутри этих двух пар целевых функций отсутствуют вовсе (и, следовательно, содержащаяся в них информация не дублируется).

Взаимозависимость последней пары целевых функций (максимальная просадка и процент прибыльных сделок) демонстрирует повышательный тренд. При низких значениях параметра коэффициент корреляции отрицателен, а, когда параметр достигает своих максимальных значений, корреляция становится положительной (коэффициент корреляции равен нулю, когда «период истории для расчета HV» составляет порядка 200 дней). Вновь заметим, что, когда те же данные рассматривались консолидировано (правый нижний график рис. 2.3.2), то мы не смогли обнаружить какую-либо взаимозависимость между этими целевыми функциями. Из этого можно было сделать не совсем верный вывод о полном отсутствии дублирования информации. Между тем детализированный анализ (рис. 2.3.3) позволяет уточнить, что информация не дублируется только во второй трети диапазона допустимых значений параметра.

Теперь перейдем к рассмотрению влияния второго параметра, «число дней до экспирации опционов» на взаимозависимость целевых функций (рис. 2.3.4). Данный параметр влияет на скоррелированность целевых функций в гораздо большей степени, чем «период истории для расчета HV» (сравни рис. 2.3.3 и 2.3.4). Даже небольшие изменения параметра приводят к весьма существенным изменениям корреляций. Коэффициенты корреляции почти всех пар целевых функций колеблются в очень широком диапазоне (от –0,9 до 0,9). Однако в отличии от предыдущего случая (когда рассматривалось влияние параметра «период истории для расчета HV») влияние количества дней, остающихся до истечения опционов, весьма хаотично. В динамике коэффициентов корреляции отсутствуют всякие признаки трендов.

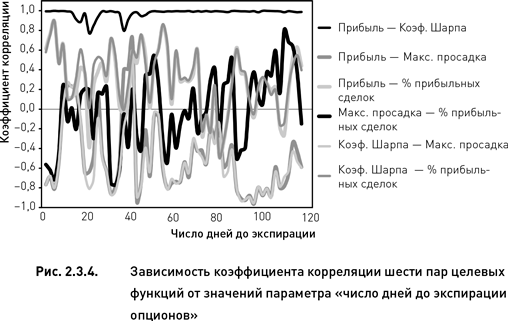
Единственное исключение составляет пара целевых функций «прибыль» и «коэффициент Шарпа». В этом случае коэффициент корреляции не зависит от количества дней до экспирации и сохраняет максимально высокое значение почти на всем диапазоне допустимых значений параметра (рис. 2.3.4). Точно такая же картина наблюдалась для этой пары целевых функций при изучении влияния параметра «период истории для расчета HV» (рис. 2.3.3).

Можно сделать вывод, что, принимая решение о включении той или иной целевой функции в систему многокритериальной оптимизации, следует руководствоваться степенью взаимозависимости рассматриваемых функций. Предпочтение нужно отдавать тем из них, которые коррелируют в наименьшей степени. Это обеспечит внесение в систему максимального количества новой, недублирующейся информации. Определяя степень допустимой взаимозависимости (порог коэффициента корреляции, выше которого целевая функция не принимается), необходимо убедиться в том, что корреляция целевых функций не зависит от значений параметров. В случае если такая зависимость существует (как было показано выше), то для принятия решения нужно использовать такой коэффициент корреляции, который был рассчитан на данных, в наибольшей степени соответствующих логике разрабатываемой торговой стратегии.