Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 4. На плечах гигантов
Дальше: Глава 6. Великое соединение
Глава 5. Дзета-функция Римана
I.
Базельская задача
Выразить в замкнутом виде бесконечный ряд
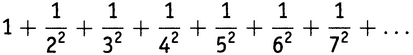
Базельская задача названа в честь швейцарского города, в университете которого профессорами математики один за другим были двое братьев Бернулли — Якоб (с 1687 по 1705 год) и Иоганн (с 1705 по 1748 год). Мы упоминали в главе 1.iii, что оба брата Бернулли нашли доказательства расходимости гармонического ряда. В книге, где он опубликовал сначала доказательство брата, а потом и свое, Якоб Бернулли сформулировал приведенную выше задачу и обратился ко всем, кто знает, как с ней разобраться, с просьбой сообщить ему ответ. (Я очень скоро объясню, что значит «выразить в замкнутом виде».)
Заметим, что ряд, фигурирующий в этой задаче, — будем называть его «базельским рядом» — не слишком далек от гармонического ряда. Каждый член в нем, собственно говоря, равен квадрату соответствующего члена в гармоническом ряде. А возведение в квадрат числа, меньшего единицы, дает число еще меньшее: квадрат одной второй уменьшает ее до одной четвертой. И чем меньшее число возводится в квадрат, тем сильнее выражен этот эффект: одна четвертая лишь немного меньше одной второй, но квадрат одной десятой дает одну сотую, которая намного меньше, чем одна десятая.
Каждый член в базельском ряду, таким образом, меньше соответствующего члена в гармоническом ряду, и по мере продвижения вперед они делаются все меньше и меньше. Поскольку гармонический ряд лишь «едва-едва» расходится, вполне реальны надежды на то, что базельский ряд, составленный из меньших и даже много меньших величин, сойдется. Вычисление подсказывает, что на самом деле так и есть. Сумма первых десяти членов равна 1,5497677…, сумма ста членов составляет 1,6349839…, тысячи — 1,6439345…, а десяти тысяч — 1,6448340…. Действительно, впечатление такое, что ряд сходится к какому-то числу в окрестности 1,644 или 1,645. Но к какому?
В подобных ситуациях математиков не устраивает просто найти приближение, особенно когда рассматриваемый ряд сходится медленно, как в данном случае. (Сумма 10 000 членов все еще на 0,006 процента отличается от значения полной, бесконечной суммы, которая равна 1,6449340668….) Выражается ли ответ дробным числом, скажем, 9108/5537 или 560 837 199/340 948 133? Или он имеет более сложный вид, может быть, в него входят корни, например, √46/17, или же корень пятой степени из 11 983/995, или же корень восемнадцатой степени из 7776? Чему равен ответ? Неспециалист решил бы, что вполне достаточно знать это число с точностью до нескольких знаков после запятой. Но нет, математики желают знать его точно, если только это возможно. Не просто потому, что они одержимы навязчивой идеей, но и потому, что по опыту знают: получение точного ответа нередко открывает ранее запертые двери и проливает свет на более глубокие математические вопросы. Математический профессиональный термин для такого точного представления — это «замкнутый вид». А десятичное приближение, неважно, насколько точное, — «незамкнутый вид». Число 1,6449340668… — это незамкнутый вид. Сами видите, что многоточие сообщает нам, что правая часть не завершена и при желании можно проделать вычисление, чтобы добавить туда еще цифры.
Базельская задача была поставлена так: найти замкнутый вид ряда из обратных квадратов. Задача была в конце концов побеждена в 1735 году, через 46 лет после своей постановки, и сделал это молодой Леонард Эйлер, трудившийся в далеком Санкт-Петербурге. Потрясающий ответ имеет вид π2/6. Да, это «то самое» π, магическое число, равное 3,14159265…, — отношение длины окружности к ее диаметру. Что же оно делает в задаче, которая не имеет ни малейшего отношения не только к окружностям, но и вообще к геометрии?! Современных математиков это не так уж изумляет, они привыкли, что π можно встретить в математике где угодно, но в 1735 году этот ответ произвел сильное впечатление.
Базельская задача подводит нас к дзета-функции — объекту, с которым мы имеем дело в Гипотезе Римана. Но прежде чем мы сможем познакомиться с дзета-функцией, надо вспомнить кое-что из математических основ: степени, корни и логарифмы.
II.
Степени — это прежде всего повторяющееся умножение. Число 123 — это 12×12×12, где перемножаются три сомножителя, а 125 — это 12×12×12×12×12, где сомножителей пять. Что получится, если умножить 123 на 125? Это будет (12×12×12)×(12×12×12×12×12), что, конечно, составляет 128. Надо просто сложить степени: 3 + 5 = 8. В этом и состоит первое великое правило действий со степенями.
1-е правило действий со степенями:
xm×xn = xm + n.
(Давайте я здесь прямо и скажу, что во всем этом разделе мы будем иметь дело только с положительными значениями буквы x. Возводить в степень нуль — пустая трата времени, а возведение в степень отрицательных чисел приводит к занятным проблемам, о которых мы поговорим позднее.)
Что будет, если разделить 125 на 123? То есть вычислить (12×12×12×12×12)/(12×12×12). Можно сократить три множителя 12 сверху и снизу, и в результате останется 12×12, т.е. 122. Как видно, это все равно что вычесть степени.
2-е правило действий со степенями:
xm: xn = xm − n.
А теперь возведем 125 в куб: (12×12×12×12×12)×(12×12×12×12×12)×(12×12×12×12×12) дает 1215. На этот раз степени перемножаются.
3-е правило действий со степенями:
(xn)m = xmn.
Таковы три самых важных правила, которые говорят нам, как обращаться со степенями. В дальнейшем мы будем ссылаться на них как на «правила действий со степенями» без дополнительных объяснений. Однако это пока не все правила. Нам потребуется еще несколько, потому что до сих пор у нас были степени, выражаемые положительными целыми числами. А как обстоит дело с отрицательными и дробными степенями? А со степенью нуль?
Начав с последнего, заметим, что если x0 вообще что-нибудь будет означать, то хорошо бы добиться согласованности с теми правилами, которые у нас уже есть, потому что они являются прямым выражением здравого смысла. Возьмем во 2-м правиле n равным m. Тогда в правой части, как видно, получится x0. А в левой части будет xm: xm. Но когда число делится само на себя, получается единица.
4- e правило действий со степенями:
x0 = 1 для всякого положительного числа x.
2-е правило можно использовать и для того, чтобы придать смысл отрицательным степеням. Разделим 123 на 125. Согласно 2-му правилу, ответ должен быть равен 12−2. Но при этом он равен и (12×12×12)/(12×12×12×12×12), что после сокращения трех множителей 12 в числителе и знаменателе даст 1/122.
5-е правило действий со степенями:
x−n = 1/xn (в частности, x−1 = 1/x).
3-е правило наводит нас на мысль о том, что же должны означать дробные степени. Как можно поступить с величиной x1/3? Например, возвести ее в куб, тогда по 3-му правилу должно получиться просто x. Значит, x1/3 есть просто кубический корень из x. (Определение «кубического корня из x»: это число, куб которого равен x). 3-е правило теперь говорит нам, какой смысл имеет всякая дробная степень; x2/3 — это кубический корень из x, возведенный в квадрат (или, что одно и то же, кубический корень из x2).
6-е правило действий со степенями:
хm/n есть корень n-й степени из хm.
Поскольку 12 — это 3×4, получаем, что 125 равно (3×4)×(3×4)×(3×4)×(3×4)×(3×4). Это можно переписать как (3×3×3×3×3)×(4×4×4×4×4). Короче говоря: 125 = 35×45. Такое верно и в общем случае:
7-е правило действий со степенями:
(x×y)n = xn×yn.
А что насчет возведения x в иррациональную степень? Что могло бы означать 12√2, или 12π, или 12e? Здесь мы снова попадаем в царство анализа. Вспомним про ту последовательность из главы 1.vii, которая сходилась к √2. Она выглядела так: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, … Продолжая эту последовательность достаточно далеко, можно подобраться к √2 сколь угодно близко. А из 6-го правила, которое говорит о значении всякой дробной степени, понятно, что же представляет собой число 12, возведенное в каждую из этих дробных степеней. Разумеется, число 121 равно просто 12, а 123/2 — это квадратный корень из 12 в кубе; 41,569219381…. Далее, 127/5 — это корень пятой степени из 12 в седьмой степени, что равно 32,423040924…. Таким же образом, 1217/12 равно 33,794038815…, 1241/29 равно 33,553590738…, 1299/70 равно 33,594688567… и т.д. Как мы видим, эти дробные степени числа 12 сходятся к некоторому числу — на самом деле к числу 33,588665890…. Поскольку сами дроби при этом сходятся к √2, очень похоже на правду, что 12√2 = 33,588665890….
Итак, задавшись положительным числом x, можно возводить его вообще в любую степень — положительную, отрицательную, дробную или иррациональную. При этом будут выполняться приведенные выше правила действий со степенями, поскольку мы ввели определения таким образом, чтобы именно это и гарантировать! На рисунке 5.1 показаны графики функций xa для различных чисел a в интервале от −2 до 8. Отдельно отметим нулевую степень х0, представляющую собой горизонтальную прямую на высоте 1 над осью x — то, что математики называют «постоянной функцией» (а медсестры в реанимации называют «остановкой»). Для любого аргумента x значение этой функции равно 1. Стоит еще обратить внимание, как быстро возрастают целочисленные степени x2, x3, x8, а также — что имеет более прямую связь с главной темой этой книги — как медленно возрастают дробные положительные степени, такие как x0,5.

Рисунок 5.1. Степенные функции xa для различных чисел a.
III.
Возведение чисел в степени на первый взгляд выглядит похожим на умножение. Умножение сначала представляют как кратное сложение: 12×5 = 12 + 12 + 12 + 12 + 12, затем на следующем уровне сложности объясняется, что такое 12×51/2 где на самом деле содержится кое-что еще, кроме кратного умножения. Похожим образом обстоит дело и с возведением в степень. Определить 125 совсем легко, это кратное умножение: 12×12×12×12×12. Чтобы справиться с 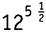 , требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.
, требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.
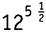 , требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.
, требуются дополнительные объяснения, подобные тем, что предложены в предыдущем разделе.Как я уже говорил, математики обожают обращать выражения. Скажем, пусть задано выражение величины P через Q. Отлично, давайте посмотрим, можно ли выразить Q через P. И здесь аналогия между умножением и возведением в степень нарушается. Обратить умножение легко: если x = a×b, то a = x:b и b = x:a. Деление полностью решает проблему обращения умножения.
Аналогия нарушается, потому что a×b всегда и без единого исключения равно a×b, но, к сожалению, неверно (за исключением случайных совпадений), что ab = ba (единственный случай, когда это так для целочисленных степеней и не совпадающих a и b — это 24 = 42). Например, 102 есть 100, но 210 есть 1024. Поэтому, если мы собираемся обратить x = ab, то нам понадобятся две разные вещи: способ выразить a через x и b и, отдельно, способ выразить b через x и a. Первое — не проблема. Возведем обе части в степень 1/b и в соответствии с 3-м правилом получим a = x1/b (что согласно 6-му правилу означает, что a есть корень b-й степени из x). Но как же выразить b через x и а? Правила действий со степенями не дают здесь никаких подсказок.
Здесь-то и появляются логарифмы. Ответ таков: b есть логарифм x по основанию a. Это просто-напросто определение логарифма. Логарифм числа x по основанию a (обычно записываемый как loga x) определяется как такое число b, для которого верно равенство x = ab. Это дает целое семейство логарифмических функций: логарифм x по основанию 2, логарифм x по основанию 10 (который более старшие читатели могут припомнить в качестве облегчающего вычисления средства, — его проходили в старших классах школы примерно до 1980 года) и т.д. Можно было бы представить их все в виде графиков, как это сделано для графиков функций х0 на рисунке .
Я не буду этого делать, потому что мне глубоко безразличны все члены логарифмического семейства, кроме одного — логарифма по основанию e, где e — необычайно важное, хотя и иррациональное число 2,71828182845…. Логарифм по основанию e — единственный, который меня интересует, и единственный, которым мы будем пользоваться в этой книге. На самом деле я больше не буду говорить «логарифм по основанию e», а буду говорить просто «логарифм». Так что же такое логарифм числа x? По данному выше определению, это такое число b, для которого делается верным равенство x = eb.
Поскольку ln x — это такое число b, для которого верно равенство x = eb, ясно, что x = eln x. Это равенство — просто записанное математически определение того, что такое ln x. Но в дальнейшем оно будет играть такую важную роль, что мы сделаем из него правило.
8-е правило действий со степенями:
x = eln x.
Это верно для любого положительного числах. Например, ln 7 есть 1,945910… по той причине, что (с точностью до шести знаков после запятой) 7 = 2,7182811,945910. Отрицательные числа не имеют логарифмов (хотя это еще одна вещь, по поводу которой я оставляю за собой право потом передумать). И нуль также не имеет логарифма. Не существует такой степени, в которую можно было бы возвести в, чтобы получить отрицательный или нулевой результат. Область определения логарифма составляют все положительные числа.
Логарифмическая функция присутствует повсеместно в рассматриваемой области математики. Мы уже встречали ее в главе 3.viii-ix, где она участвовала в Теореме о распределении простых чисел и в ее эквивалентных формулировках. Она будет появляться снова и снова в этой книге во всем, что имеет отношение к простым числам и дзета-функции.
Раз уж логарифмическая функция будет встречаться на каждом шагу, рассмотрим ее подробнее. На рисунке 5.2 показан график функции ln x для аргументов, простирающихся до 55. В частности, отмечены значения этой функции для аргументов, равных 2, 6, 18 и 54. Эти аргументы растут «по умножению» на тройку, а как видно из графика, соответствующие значения функции растут равными шагами — т.е. «по сложению». Именно это обстоятельство подчеркивалось, когда мы говорили о логарифмической функции в главе 3.viii.
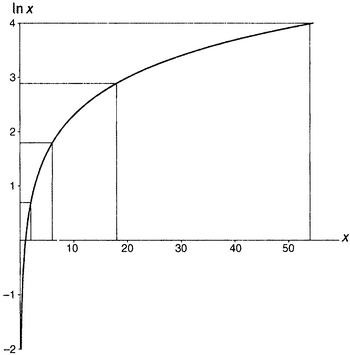
Рисунок 5.2. Логарифмическая функция.
Дело стоит того, чтобы сказать еще несколько слов. Логарифмическая функция хороша тем, что она превращает умножение в сложение. Взглянем на линии, отмеченные на графике. Аргументы равны 2, 6, 18 и 54 — мы начинаем с 2, потом умножаем на 3, потом снова на 3, потом еще раз на 3 и еще раз на 3. Значения функции, если ограничиться четырьмя знаками после запятой, равны 0,6931, 1,7918, 2,8904 и 3,9890 — они начинаются с 0,6931, потом прибавляется 1,0987, затем 1,0986 и еще раз 1,0986. Логарифмическая функция превратила умножение (на 3 в нашем случае) в сложение (прибавление числа ln 3, равного 1,09861228866811…).
Это следует из определения ln x и из правил действий со степенями. Из 8-го правила следует, что если a и b — любые два положительных числа, то a×b = eln a×eln b. Но, заменяя правую часть согласно 1-му правилу, получаем a×b = eln a + ln b. Однако a×b — само по себе некоторое число, и, согласно 8-му правилу, имеем a×b = eln (a×b). Мы получили два различных выражения для a×b. Приравнивая их, получаем новое правило действий со степенями.
9-е правило действий со степенями:
ln (a×b) = ln a + ln b.
Это потрясающая штука. Она означает, что, когда мы сталкиваемся со сложной задачей на умножение, «взятие логарифмов» (т.е. применение того принципа, что из равенства P = Q следует равенство ln P = ln Q) позволяет свести ее к задаче на сложение, которая может оказаться проще. Звучит это почти банально, и тем не менее именно этот нехитрый приемчик понадобится нам в главе 19.v для того, чтобы повернуть Золотой Ключ.
Из того, что ln (a×b) = ln a + ln b, следует, что ln (a×a×a×…) = ln a + ln a + ln a + …. И это дает последнее правило действий со степенями.
10-е правило действий со степенями:
ln (aN) = N×ln a.
Не повторяя необходимую цепь логических рассуждений, просто отметим, что это правило применимо ко всем степеням буквы а, включая и отрицательные. Особо важный частный случай состоит в том, что ln (1/a) = −ln a, поскольку 1/а есть не что иное, как a−1. Так что если нам известно, что ln 3 = 1,09861228866…, то мы немедленно заключаем, что ln 1/3 = −1,09861228866…. Вот почему график функции ln x проваливается вниз к отрицательной бесконечности по мере того, как x делается все ближе и ближе к нулю. Это обстоятельство тоже поможет нам повернуть Золотой Ключ.
IV.
Как мы видим, ln x — медленно возрастающая функция. Неторопливость, с которой ln x возрастает, не только сама по себе обворожительна, но и важна. Главное здесь то, что ln x растет медленнее, чем любая степень буквы x. На первый взгляд это кажется довольно очевидным. Когда я говорю «степень буквы x», вы, должно быть, думаете о квадратах и кубах; а как вы знаете, график функции возведения в квадрат или куб так лихо вылетает за границы рисунка, что его и сравнивать нечего с еле плетущейся логарифмической функцией. Это, конечно, верно, но дело не в этом. Я имею в виду не степени вроде х2 или х3, а степени типа х0,1.
На рисунке 5.3 показаны графики некоторых функций xa для малых значений a. Там выбраны a = 0,5, 0,4, 0,3, 0,2 и 0,1, а пунктиром для сравнения показана логарифмическая функция. Как видно, чем меньше a, тем более плоским делается график функции xa. А кроме того, для тех a, которые меньше определенного значения (на самом деле — значения 1/e, что равно 0,3678794…), кривая, отвечающая функции ln x, пересекает кривую xa до того, как уйти достаточно далеко на восток.
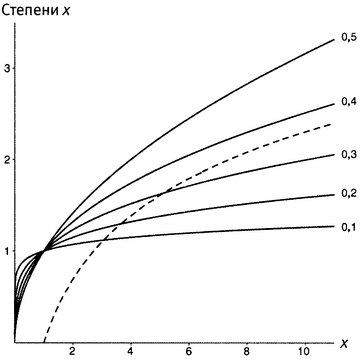
Рисунок 5.3. Функции xa при малых положительных a.
Так вот, неважно, сколь маленьким вы возьмете a, все равно график функции ln x рано или поздно окажется более плоским, чем график xa. Если а больше чем 1/e, то это видно сразу, даже на изображенных графиках. Если же a меньше чем 1/e, то, уйдя достаточно далеко на восток — т.е. взяв достаточно большой аргумент x, мы увидим, как кривая ln x снова пересекает кривую xa, после чего уже навсегда остается ниже нее.
Разумеется, путешествие может оказаться неблизким. Кривая ln x повторно пересекает кривую x0,3 чуть к востоку от точки x = 379; она повторно пересекает кривую x0,1 только после того, как пройдет через точку x = 332 105; и она повторно пересекает кривую x0,001 только после прохождения точки x = 3 430 631 121 407 801. Если бы мы нарисовали график функции x в степени одна триллионная (т.е. x0,000000000001), то она выглядела бы до безобразия плоской. Настолько, что ее нелегко было бы отличить от функции «остановки сердца», которая имеет высоту 1 над осью x, — ничего похожего на изящно восходящую кривую логарифмической функции. Логарифмическая кривая пересекла бы ее на малюсеньком расстоянии к востоку от e. И однако же степенная функция растет, хотя и чрезвычайно медленно, в то время как логарифмическая функция постепенно становится все более пологой. Рано или поздно они снова пересекутся, и тогда уже логарифмическая кривая навеки останется под кривой x0,000000000001. Точка пересечения в этом случае наступит при таком большом аргументе, что я не могу его здесь записать: это число начинается как 44 556 503 846 304 183… и содержит еще 13 492 301 733 606 цифр.
Картина такова, как будто ln x старается быть функцией x0. Конечно, это не x0: для любого положительного числа выражение x0 определяется равным числу 1, согласно 4-му правилу, и соответствующий график, как мы видели, — это «остановка сердца». Но хотя функция ln x и не есть x0, она умудряется при достаточно больших x поднырнуть под функцию xε со сколь угодно малым ε и оставаться там уже навсегда.
В действительности дело обстоит даже еще более странным образом. Рассмотрим утверждение: «функция ln x рано или поздно будет расти медленнее, чем x0,001, и x0,000001, и x0,000000001, и …» Представим себе, что мы возвели все это утверждение в некоторую степень — скажем, в сотую. (Это, надо признать, не очень строгая математическая операция, но она приводит к верному результату.) После применения 3-го правила утверждение будет выглядеть так: «функция (ln x)100 рано или поздно будет расти медленнее, чем x0,1, и x0,0001, и x0,0000001, и …». Другими словами, если логарифм растет медленнее, чем любая степень буквы x, то это же верно и для любой степени функции ln x. Каждая из функций (ln x)2, (ln x)3, (ln x)4, …, (ln x)100, … растет медленнее, чем любая степень x. Независимо оттого, сколь велико N и сколь мало ε, график функции (ln x)N в конце концов поднырнет под график функции xε и останется там, внизу.
Такое нелегко себе представить. Функции (ln x)N растут быстро — и даже очень быстро. И тем не менее, если на рисунке отойти достаточно далеко на восток, то рано или поздно, при некотором впечатляюще большом аргументе, каждая из них опустится ниже кривой x0,3, x0,2, x0,1 и вообще любой кривой из этого семейства, какую вы только потрудитесь нарисовать. Придется отправиться на восток в окрестность точки x = 7,9414×103959, прежде чем (ln x)100 опустится ниже, чем x0,3; и однако же это случится.
V.
Кое-что из сказанного понадобится нам прямо сейчас, а кое-что останется на потом. Но все сказанное важно для понимания Гипотезы Римана, и я призываю вас проконтролировать некоторые основные моменты — проверить, как вы их понимаете, прежде чем двигаться дальше. Для этого сгодится карманный калькулятор. Можете, например, найти ln 2 (он равен 0,693147…) и ln 3 (равный 1,098612…) и удостовериться, что при сложении их действительно получается ln 6 (равный 1,791759…). Но только обратите, пожалуйста, внимание, что (как я уже упоминал) прежде использовались логарифмы по основанию 10, так что клавиша «log» на многих карманных калькуляторах вычисляет именно десятичные логарифмы. Тот единственный логарифм, который нас здесь интересует, — логарифм по основанию e — на калькуляторе, как правило, вычисляется с помощью альтернативной клавиши, помеченной ln x. Вот эта клавиша вам и нужна. (Буква n указывает на «натуральный» логарифм; логарифм по основанию e по всем правилам называется «натуральный логарифм».)
Ну а теперь вернемся к базельской задаче.
VI.
Эйлерово решение базельской задачи прекрасно иллюстрирует сделанное в разделе I этой главы замечание, что поиск решений в замкнутом виде расширяет понимание, позволяя проникнуть в суть вещей. Эйлерово решение дало не только замкнутое выражение для ряда из обратных квадратов, но в качестве побочного продукта еще и замкнутые выражения для рядов 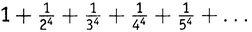 ,
, 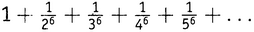 и т.д. Для четных N результат Эйлера дает в замкнутом виде точное значение для следующего бесконечного ряда (5.1):
и т.д. Для четных N результат Эйлера дает в замкнутом виде точное значение для следующего бесконечного ряда (5.1):
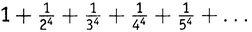 ,
, 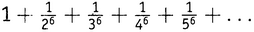 и т.д. Для четных N результат Эйлера дает в замкнутом виде точное значение для следующего бесконечного ряда (5.1):
и т.д. Для четных N результат Эйлера дает в замкнутом виде точное значение для следующего бесконечного ряда (5.1):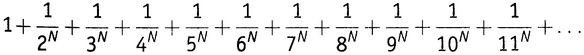
Когда N равно двум, ряд сходится к π2/6, как уже было сказано; когда N равно 4, ряд сходится к π4/90; когда N равно 6, ряд сходится к π6/945 и т.д. Метод Эйлера дает ответ для каждого четного N. В более поздней публикации он сам добрался до N = 26, когда ряд сходится к числу 1 315 862π26/11 094 481 976 030 578 125.
А что, если N нечетное? Полученный Эйлером результат ничего про это не говорит. Как не говорит и ни один другой результат, полученный за последующие 260 лет. Нет никаких идей относительно замкнутого выражения (если таковое вообще существует) ни для 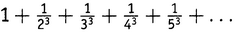 , ни для аналогичного ряда при других нечетных показателях степени. Никто не смог найти замкнутое выражение для этих рядов. Мы знаем, что они сходятся, и можем, конечно, методом грубой силы вычислить их значение с любой требуемой точностью. Мы просто не знаем, что они означают. Только в 1978 году было доказано, что ряд
, ни для аналогичного ряда при других нечетных показателях степени. Никто не смог найти замкнутое выражение для этих рядов. Мы знаем, что они сходятся, и можем, конечно, методом грубой силы вычислить их значение с любой требуемой точностью. Мы просто не знаем, что они означают. Только в 1978 году было доказано, что ряд 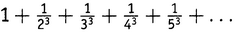 определяет иррациональное число.
определяет иррациональное число.
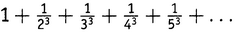 , ни для аналогичного ряда при других нечетных показателях степени. Никто не смог найти замкнутое выражение для этих рядов. Мы знаем, что они сходятся, и можем, конечно, методом грубой силы вычислить их значение с любой требуемой точностью. Мы просто не знаем, что они означают. Только в 1978 году было доказано, что ряд
, ни для аналогичного ряда при других нечетных показателях степени. Никто не смог найти замкнутое выражение для этих рядов. Мы знаем, что они сходятся, и можем, конечно, методом грубой силы вычислить их значение с любой требуемой точностью. Мы просто не знаем, что они означают. Только в 1978 году было доказано, что ряд 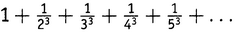 определяет иррациональное число.
определяет иррациональное число.Итак, к середине XVIII века немало математиков задумывались над бесконечным рядом из выражения . Точные значения — замкнутый вид — были известны для всех четных чисел N, тогда как для нечетных можно было получать приближенные значения, беря сумму достаточного числа членов. Не будем забывать, что, когда N равно 1, соответствующий ряд становится просто гармоническим рядом, который расходится. В таблице 5.1 приведены значения выражения (которое, напомним, есть 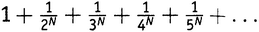 ) с точностью до 12 знаков после запятой.
) с точностью до 12 знаков после запятой.
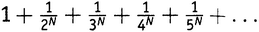 ) с точностью до 12 знаков после запятой.
) с точностью до 12 знаков после запятой.| 1 | (нет значения) |
| 2 | 1,644934066848 |
| 3 | 1,202056903159 |
| 4 | 1,082323233711 |
| 5 | 1,036927755143 |
| 6 | 1,017343061984 |
Таблица 5.1.
Эта таблица похожа на один из тех «мгновенных снимков» некоторой функции, которые мы рассматривали в главе 3.iv. Так примерно дело и обстоит. Вспомним утверждение Гипотезы Римана, приведенное во вступлении.
Гипотеза Римана
Все нетривиальные нули дзета-функции имеют вещественную часть, равную одной второй.
Таблица 5.1 дает нам первое представление о дзета-функции Римана и тем самым представляет собой первый шаг к пониманию Гипотезы Римана.
VII.
Коль скоро в предшествующих разделах данной главы мы потрудились придать смысл степенной функции xa для любого числа a, а не просто для целых чисел, сейчас нет причины ограничивать букву N в выражении целыми числами. Можно представить себе, как это число свободно парит, принимая различные значения — дробные, отрицательные и иррациональные. Нет, правда, гарантии, что ряд будет сходиться для всех чисел — как мы уже знаем из главы 1.iii, он не сходится при N = 1. Но можно, по крайней мере, попытать счастья, исследуя разные возможности.
В связи с осознанием этой новой мысли, сменим обозначение N на другую букву, которая имеет меньше традиционных ассоциаций с целыми числами. Очевидным выбором, конечно, была бы буква x. Но Риман в своей работе 1859 года не использовал икса. Подобные вопросы в его время не были урегулированы. Вместо этого он пользовался буквой s; а его работа 1859 года приобрела такое значение, что все математики, жившие после Римана, вслед за ним использовали ту же букву. В исследованиях, посвященных дзета-функции, аргумент всегда обозначается буквой s.
И вот наконец перед нами дзета-функция Римана (дзета, которая пишется как ζ, — это шестая буква греческого алфавита) (5.2):
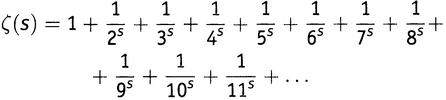
VIII.
Прежде чем двигаться дальше, давайте введем полезные математические обозначения, которые сократят работу по набору формул. (Думаете, легко вставить штуки, подобные выражению , в Microsoft Word?)
Если математики хотят сложить некоторое множество членов, которые все построены по общему закону, то они используют знак ∑. Это заглавная буква «сигма», восемнадцатая буква греческого алфавита, обозначающая греческую «с» (первую букву в слове «сумма»). Применяется она следующим образом. Суммируемый член, записанный с помощью данного правила, помещается «под» (на самом деле имеется в виду — справа, хотя вопреки логике говорится «под») знаком сигмы. А снизу и сверху от сигмы указывается, где сумма начинается и где заканчивается. Например, выражение
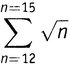
представляет собой математическую «стенографию» — краткую запись выражения √12 + √13 + √14 + √15. Сигма говорит нам: «Сложить их!»; выражения сверху и снизу от сигмы показывают, где начать сложение и где его закончить; и наконец, выражение под знаком сигмы говорит, что, собственно, надо складывать — в данном случае √n.
Математики не особенно педантичны по поводу стиля таких выражений. Приведенную выше сумму часто записывают как

поскольку ясно, что именно n пробегает значения от 12 до 15. Теперь, вовсю используя знак сигмы, мы можем не тратить силы на лишние символы, а записать выражение в виде
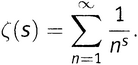
А с учетом 5-го правила действий со степенями это же можно записать как
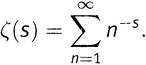
И более того, поскольку n с очевидностью (и часто) используется для обозначения положительных целых чисел 1, 2, 3, 4, …, математики сокращают запись еще сильнее и просто пишут
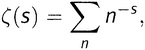
что выражает ту же самую дзета-функцию Римана. Читается это так: «дзета от s определена как взятая по всем n сумма от n в степени минус s». Здесь «по всем n» понимается как «по всем целым положительным п».
IX.
Получив дзета-функцию в виде изящного выражения, посмотрим повнимательнее на ее аргумент s. Из главы 1.iii мы уже знаем, что при s, равном единице, ряд расходится, и, следовательно, у дзета-функции нет значения. При s, равном 2, 3, 4, …, он всегда сходится и тем самым дает значения дзета-функции (см. таблицу ). На самом деле можно показать, что ряд сходится при любом s, большем единицы. При s, равном 1,5, ряд сходится к 2,612375…. При s, равном 1,1, он сходится к 10,584448…. А при s, равном 1,0001, он сходится к 10000,577222…. Может показаться странным, что ряд расходится при s = 1, но при этом умудряется сходиться при s = 1,0001. Это, однако, нормальная ситуация в математике. На самом деле, когда s очень близко к 1, дзета-функция замечательным образом ведет себя подобно функции 1/(s − 1). Эта функция также имеет значения при всех s, кроме того случая, когда s в точности равняется 1, поскольку знаменатель тогда равен нулю, а на нуль делить нельзя.
Некоторую ясность может внести график. На рисунке 5.4 показан график дзета-функции. Как видно, когда аргумент s приближается к 1 справа, значения функции убегают на бесконечность, а когда s само уходит на бесконечность далеко справа, функция все более и более приближается к 1. (Я пририсовал еще два пунктира: линию s = 1 и график постоянной функции.)
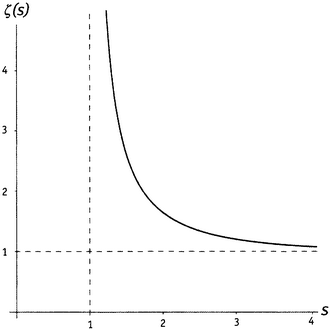
Рисунок 5.4. Дзета-функция для аргументов, превышающих 1.
На графике не показано ничего про дзета-функцию слева от линии s = 1. Это потому, что до сих пор мы предполагали, что s больше единицы. А если меньше? Если, скажем, s равно нулю? Ну, тогда выражение примет вид
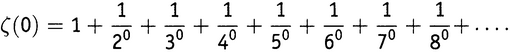
Но согласно 4-му правилу эта сумма равна 1 + 1 + 1 + 1 + 1 + 1 + …, что довольно очевидным образом расходится. Возьмем сумму ста членов: она будет равна 100; тысячи — 1000. Сложение миллиона слагаемых дает значение 1000 000. Да, ряд расходится.
С отрицательными числами дело обстоит еще хуже. Каково значение выражения , если s равно −1? Из 5-го правила следует, что 2−1 — это просто 1/2, 3−1 — просто 1/3 и т.д. Поскольку 1:1/2 есть просто 2, 1:1/3 — просто 3 и т.д., наш ряд принимает вид 1 + 2 + 3 + 4 + 5 + …, что определенно расходится. А как насчет s = 1/2? Поскольку 21/2 — это просто √2 и т.д., ряд принимает вид
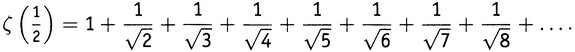
Поскольку квадратный корень из любого целого числа меньше самого числа, каждый член этого ряда больше, чем соответствующий член ряда 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + …. (Элементарная алгебра: если a меньше, чем b, то 1/a больше, чем 1/b. Например, 2 меньше, чем 4, но 1/2 больше, чем 1/4). Указанный ряд расходится, а значит, интересующий нас ряд также расходится. Ну и правда, если вы потрудитесь вычислить суммы, то окажется, что первые десять членов суммируются к 5,020997899…, первые сто — к 18,589603824…, первые тысяча — к 61,801008765…, а первые десять тысяч — к 198,544645449… и т.д.
Похоже, что на графике изображено все, что можно показать про дзета-функцию Римана. Кроме этого, ничего больше нет. Функция имеет значения, только когда s больше единицы. Или, как мы теперь можем сказать с использованием должного профессионального термина, область определения дзета-функции составляют все числа, большие единицы. Верно? Нет!
Назад: Глава 4. На плечах гигантов
Дальше: Глава 6. Великое соединение

