Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 3. Теорема о распределении простых чисел
Дальше: Глава 5. Дзета-функция Римана
Глава 4. На плечах гигантов
Первым человеком, которому открылась истина, содержащаяся в Теореме о распределении простых чисел (ТРПЧ), был Карл Фридрих Гаусс, живший с 1777 по 1855 год. Гаусс, как уже говорилось в главе 2.v, вполне может претендовать на звание величайшего математика из всех вообще когда-либо живших. В течение своей жизни он был известен как Princeps Mathematicorum — Князь Математиков, а после его смерти король Ганновера Георг V распорядился о выпуске памятной медали в его честь, с указанием этого титула.
Гаусс был чрезвычайно невысокого происхождения. Его дед был безземельным крестьянином, а отец — перебивавшимся с места на место садовником и каменщиком. Гаусс ходил в самую скромную местную школу. Знаменитый эпизод, который, как рассказывают, произошел в этой школе, имеет гораздо больше шансов оказаться правдой, чем большинство обычных историй такого рода. Однажды учитель, желая устроить себе получасовой перерыв, дал классу задание сложить друг с другом первые 100 чисел. Почти мгновенно Гаусс бросил грифельную доску на учительский стол со словами «Ligget se!», что на местном крестьянском диалекте того времени означало: «Вот он [ответ]!» Карл мысленно расположил числа горизонтально в порядке (1, 2, 3, …, 100), затем в обратном порядке (100, 99, 98, …, 1), а после этого сложил два списка вертикально: (101, 101, 101, …, 101). Получилось 100 раз число 101, а поскольку числа были выписаны дважды, ответ равен половине этой суммы, т.е. 50 умножить на 101, что равно 5050. Совсем просто, когда вам об этом рассказали, но все же это не тот способ, который сам собой придет в голову обычному десятилетнему мальчику; да и обычному взрослому лет в тридцать тоже, если уж на то пошло.
Гауссу повезло в том, что учителя разглядели его способности и готовы были предпринять некоторые усилия, чтобы их развить. Еще большее везение состояло в том, что ему случилось жить в маленьком германском герцогстве Брауншвейг — в пределах той самой кляксы, что разделяет на две части королевство Ганновер на карте из главы . В Брауншвейге в то время правил Карл-Вильгельм-Фердинанд, носивший полный титул герцог Брауншвейга-Вольфенбюттеля-Беверна. Мы уже встречались с ним, хотя в тот момент этого и не подозревали: известный как отважный воин, он носил чин генерал-фельдмаршала прусской армии и командовал теми самыми соединенными прусско-австрийскими силами, которые французы остановили у Вальми 20 сентября 1792 года.
Карл-Вильгельм поступил воистину благородно. Если существует Рай для математиков, то для герцога там должны быть зарезервированы роскошные апартаменты, чтобы он мог останавливаться в них всякий раз, как соберется заехать. Услыхав о таланте мальчика Гаусса, герцог распорядился, чтобы его привели к нему. Молодой Гаусс в тот момент не мог похвастаться значительными успехами на ниве светского этикета. Позднее, в течение своей жизни, после длительного знакомства с дворами и университетами, он производил впечатление человека мягкого и приветливого, но это не могло скрыть грубоватые черты лица и коренастую фигуру, изобличавшие крестьянское происхождение. Однако герцог оказался достаточно проницательным, чтобы с первого же взгляда не ошибиться в мальчике; впоследствии он оставался его другом, пока смерть не разлучила их, и обеспечивал постоянную финансовую поддержку, позволившую молодому Гауссу сделать блестящую карьеру в качестве математика, физика и астронома.
Возможности герцога по поддержке Гаусса подошли к концу довольно плачевным образом. В 1806 году Наполеон был в зените своего могущества. В кампании предыдущего года он в битве при Аустерлице разбил соединенные войска России и Австрии, предварительно откупившись от пруссаков тем, что предложил им Ганновер. Затем он основал Рейнский союз, поставив под французское влияние всю западную часть современной Германии, и взял обратно свое обещание по сделке с Ганновером, на этот раз предложив его Британии. Против него держались только Пруссия и Саксония, а их единственным союзником была Россия, впрочем, боявшаяся пушек после поражения под Аустерлицем.
Чтобы помешать Саксонии стать французским сателлитом, пруссаки оккупировали ее, снова призвав в строй герцога Брауншвейгского — ему в то время был 71 год — и предложив ему возглавить их силы. Наполеон объявил войну, и его армия ударила на северо-запад через Саксонию по направлению к Берлину. Пруссаки пытались сконцентрировать силы, но французы, действуя очень быстро, не позволили им этого сделать и разгромили основные прусские силы под Йеной. Герцог находился с подразделением в Ауэрштедте в нескольких милях к северу; одна из фланговых частей Наполеона захватила его и рассеяла его войска.
Разбитый и смертельно раненный, герцог через эмиссара испросил у Наполеона разрешения удалиться домой, дабы там умереть. Император — вполне современный диктатор, не слишком приверженный правилам рыцарства — рассмеялся посланнику в лицо. Несчастного герцога, ослепшего и находящегося при смерти, поспешили на телеге перевезти на свободные территории за Эльбой. Секретарь Наполеона Луи де Бурьен в своих мемуарах так описывает печальный конец этой истории:
Герцог Брауншвейгский, тяжело раненный в битве при Ауэрштедте, прибыл в Альтону [на другом берегу Эльбы, прямо к западу от Гамбурга] 29 октября. Его въезд в этот город явил собой еще один яркий пример переменчивости судьбы. Люди взирали на суверенного принца, пользовавшегося, заслуженно или нет, репутацией великого воина и до недавнего времени могущественного и никем не тревожимого в своей столице; теперь же его, смертельно раненного, вносила в Альтону на жалких носилках лишь горстка людей, при нем не было адъютантов и слуг, а сопровождала его лишь ватага ребятишек. Пока герцог оставался жив, он не желал видеть никого, кроме своей жены, которая прибыла к нему 1 ноября. Он продолжал упорствовать в своем отказе принимать визитеров и умер 10 ноября.
Последний путь герцога пролегал через Брауншвейг, и говорят, что Гаусс видел повозку из окна своей комнаты, выходящего на крепостные ворота. Герцогство Брауншвейгское после этого прекратило свое существование и стало частью наполеоновского марионеточного «королевства Вестфалия». Наследник герцога Фридрих-Вильгельм был лишен трона и бежал в Англию. Он также погиб, сражаясь с Наполеоном в битве при Катр-Бра в 1815 году, за несколько дней до Ватерлоо, но, правда, уже после того, как получил обратно свое герцогство.
(Чтобы отдать должное Наполеону, следует заметить, что некоторое время спустя, во время другого похода в западную Германию, когда Гаусс уже обосновался в Геттингене, Император пощадил этот город — потому, что «там живет величайший математик всех времен».)
II.
После потери своего покровителя Гауссу пришлось искать работу. Ему предложили стать директором обсерватории в Геттингене, он согласился и приехал в Геттинген в конце 1807 года. Геттинген уже пользовался достаточной известностью за то, что был оснащен лучше других провинциальных немецких университетов. Гаусс и сам учился здесь с 1795 по 1798 год; во время учебы его, судя по всему, привлекала великолепная университетская библиотека, в которой он и проводил большую часть времени. Теперь же он стал главным университетским астрономом и оставался в Геттингене до своей смерти в феврале 1855 года, последовавшей за несколько недель до его 78-летия. В течение последних 27 лет жизни он выбирался из любимой обсерватории лишь единожды — ради поездки на конференцию в Берлин.
Чтобы рассказать об отношениях, в каких состояли между собой Гаусс и ТРПЧ, надо объяснить главную особенность Гаусса как математика. Он опубликовал намного меньше, чем написал. Из его переписки, сохранившихся неопубликованных статей и различного рода указаний, которые можно найти в опубликованных работах, видно, что он представил миру лишь часть всех сделанных им открытий. Теоремы и доказательства, которые прославили бы кого-нибудь другого, Гаусс оставлял заброшенными в своих личных дневниках.
Есть, наверное, две причины, объясняющие столь вопиющее небрежение. Одна — отсутствие честолюбия. Уравновешенный, самодостаточный и экономный человек, лишенный материальных благ в детстве и юности и так, по-видимому, и не приобретший к ним вкуса в зрелом возрасте, Гаусс не сильно нуждался в чьем бы то ни было одобрении и не стремился к продвижению по социальной лестнице. Другая причина — намного более распространенная среди математиков во все времена — состояла в перфекционизме. Гаусс не мог заставить себя представить свои результаты на суд других, пока эти результаты не окажутся отшлифованы до блеска и расставлены в безупречном логическом порядке. На его личной печати было изображено дерево с редко висящими плодами и девизом «Pauca sed matura» — «Немного, но спелые».
Как я сказал, перфекционизм — частая проблема среди математиков, из-за которой чтение опубликованных математических статей нередко превращается в очень тяжелое занятие. В одной из книг, получивших некоторую известность в современной психологической литературе, «Представление себя в повседневной жизни», Эрвинг Гоффман развивает теорию «социальной драматургии», согласно которой каждый результат деятельности, создаваемый «для внутреннего пользования» в беспорядке и не без вмешательства случайности, представляется «для внешней аудитории» в виде законченного и совершенного творения. Эту мысль хорошо иллюстрируют рестораны. Блюда, приготовленные среди стука и звона посуды, криков поваров в раскаленной кухне, предстают перед публикой как творения безупречно сервированные, на сверкающих тарелках, подаваемые проворными мурлыкающими официантами. В значительной своей части так же устроен и интеллектуальный труд. Вот что пишет Гоффман:
В тех взаимодействиях, где индивид представляет результат своей деятельности другим людям, он склонен обнародовать только конечный продукт; они же судят о нем на основе вещей законченных, отполированных и расфасованных. В ряде случаев, если для завершения деятельности было достаточно лишь очень небольшого усилия, этот факт будет скрыт. В других случаях сокрытию подлежат долгие, изнурительные часы одинокого труда…
Опубликованные математические статьи нередко содержат слегка раздражающие высказывания типа «Отсюда следует, что…» или же «Ясно, что…», тогда как в действительности совершенно не следует и абсолютно не ясно, пока вы не потратите те же шесть часов, что потратил автор, на прописывание промежуточных шагов и проверку их правильности. Об английском математике Г.X. Харди, с которым мы еще встретимся ниже, рассказывают такую историю. Дойдя на лекции до определенного места в своих рассуждениях, он сказал: «Теперь очевидно, что…» Тут он остановился, замолчал и несколько секунд простоял без движения с нахмуренными бровями. Потом вышел из аудитории. Минут через двадцать он вернулся, улыбаясь, и продолжил: «Да, действительно, очевидно, что…»
Но кроме отсутствия амбиций Гаусс демонстрировал и отсутствие такта. Он нажил массу неприятностей в общении с коллегами-математиками из-за того, что ссылался на открытия, которые он сделал, но не опубликовал за годы до того, как другие открывали то же самое, однако публиковали свои результаты. Дело было не в тщеславии — Гауссу не было свойственно тщеславие, — а в том, что доктор Джонсон называл «грубой бесчувственностью». Например, в опубликованной в 1809 году книге Гаусс ссылается на метод наименьших квадратов, придуманный им в 1794 году (способ найти наилучшую «подгонку» для некоторого количества экспериментальных данных). В момент, когда он сделал это открытие, он его, разумеется, не опубликовал. Принадлежащий к чуть более старшему поколению французский математик Адриен-Мари Лежандр открыл и опубликовал этот метод в 1806 году; он был разъярен, когда Гаусс приписал приоритет открытия себе. У нас нет сомнений в правоте Гаусса — тому имеются документальные подтверждения, — но если Гаусс желал, чтобы его имя ассоциировалось с этим результатом, ему надо было его опубликовать. Он, однако, не беспокоился, будет ли увековечено его имя, и не намеревался публиковать свои результаты, если ему не хватало времени отполировать их до полного совершенства.
III.
В декабре 1849 года Гаусс вел переписку с немецким астрономом Йоханом Францем Энке (именем которого названа знаменитая комета) Энке высказал кое-какие комментарии по поводу частоты появления простых чисел. Ответное письмо Гаусса начиналось так:
Любезное сообщение о ваших наблюдениях по поводу частоты появления простых чисел заинтересовало меня более, чем просто упоминание. Оно напомнило мне мои собственные изыскания по тому же предмету, начало которым было положено в далеком прошлом, в 1792 или 1793 году. <…> Одна из первых вещей, которые я сделал, состояла в том, что, обратив внимание на уменьшающуюся частоту, с которой появляются простые числа, я их вычислил в нескольких группах из тысячи чисел и бегло набросал результаты, листок с которыми прилагаю к письму. Я вскоре осознал, что при всех своих флуктуациях эта частота в среднем близка к величине, обратно пропорциональной логарифму… (Курсив мой. — Дж. Д.) С тех пор я время от времени (поскольку мне недостает терпения, чтобы последовательно посчитать весь интервал) уделяю свободные четверть часа, чтобы то тут, то там пересчитать еще один отрезок длиной в тысячу; но в конце концов я забросил это дело, не добравшись толком и до миллиона.
Итак, начиная с 1792 года — когда ему было лишь 15 лет! — Гаусс забавлялся пересчетом всех простых чисел в интервале из 1000 чисел за раз и довел эти вычисления до сотен тысяч («не добравшись толком и до миллиона»). Чтобы представить себе, усилия какого порядка здесь требуются, я задался целью извлечь все простые числа из отрезка в тысячу чисел от 700 001 до 701 000, пользуясь при этом лишь теми средствами, которые могли быть доступны Гауссу, — карандашом, несколькими листами бумаги и списком простых чисел до 829 — именно такие простые требуются в процессе поиска простых среди чисел до 701 000. Сознаюсь, что я бросил это занятие через час, когда я провел вычисления с простыми делителями до 47 — что означает, что мне оставалось еще 130 простых делителей. Я приглашаю вас самостоятельно попробовать такое упражнение. Это и были гауссовы «свободные четверть часа» (unbeschäftigte Viertelstunde).
Предложение, выделенное курсивом в отрывке из письма, которое Гаусс написал Энке, и составляет один из двух связанных с ТРПЧ результатов, обсуждавшихся в главе 3.ix. Как там было замечено, это утверждение эквивалентно самой ТРПЧ. Нет никаких сомнений в том, что Гаусс действительно работал над этим в начале 1790-х годов. Его заявлениям было найдено документальное подтверждение, так же как и другим заявлениям того же типа. Он просто не трудился публиковать свои результаты.
IV.
Любопытно, что первая опубликованная работа, относящаяся к ТРПЧ, принадлежит тому самому Адриену-Мари Лежандру, которого так возмутило заявление Гаусса об открытии им метода наименьших квадратов. В 1798 году — через пять или шесть лет после того, как Гаусс докопался до формулировки ТРПЧ, но не предоставил свои результаты в распоряжение человечества, — Лежандр опубликовал книгу, озаглавленную «Очерки о теории чисел», в которой он на основе своих собственных подсчетов числа простых чисел высказал предположение, что
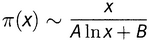
для некоторых чисел A и B, которые «подлежат определению». В более позднем издании своей книги он уточнил это предположение (доказать которое он не смог) таким образом:
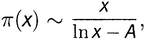
где A при больших значениях x стремится к некоторому числу, близкому к 1,08366. Гаусс обсуждает предположения Лежандра в своем письме к Энке в 1849 году он отвергает значение 1,08366, но не приходит ни к каким другим определенным выводам.
Нет сомнений, что если бы несчастный Лежандр прочитал письмо Гаусса к Энке, то оно вызвало бы у него еще один приступ гнева. По счастью, он скончался за несколько лет до того, как это письмо было написано.
V.
Раз уж эта глава посвящена обзору важных открытий и предположений, сделанных до 1800 года, и поскольку именно этот человек был создателем Золотого Ключа, о котором мы так много всего будем говорить в последующих главах, сейчас самое время представить вам другого математического гения высшей пробы, родившегося в XVIII столетии, — Леонарда Эйлера. Эйлер (1707-1783), как пишет Э.Т. Белл в своей книге «Творцы математики», был, «вероятно, величайшим из всех ученых, которых породила Швейцария»; насколько мне известно, он остается единственным математиком, именем которого названы два числа: уже упоминавшееся число e, равное 2,71828…, и число Эйлера-Маскерони, для внятного описания которого в этой книге недостаточно места, равное 0,57721… Чтобы познакомить вас с Эйлером, мне придется сначала представить вам новый географический регион, сыгравший важную роль в истории нашей темы.
Россия, как, я думаю, хорошо известно, вступила в современную эпоху несколько позднее остальной Европы, причем это вступление свершилось главным образом благодаря энергии и силе воображения Петра Великого, взошедшего на трон десятилетним мальчиком в 1682 году. Годами правления Петра обычно считаются 1682-1725, но в течение первых семи лет он правил совместно со своим подслеповатым, хромым и плохо выговаривающим слова сводным братом Иваном, а реальное управление находилось в руках сестры Ивана Софьи. Петр добился единоличного правления лишь в 1689 году в возрасте 17 лет. Но он и тогда не выказал большого интереса к государственным делам и провел следующие пять лет в забавах. По счастью, он был человеком острого ума и неуемной любознательности, и многие из его забав оказывались весьма полезными. Ему особенно нравилось общество иностранцев, которые к тому времени в значительном числе расселились в пригороде Москвы, в так называемой Немецкой слободе. Здесь, среди шотландских наемников, голландских купцов и немецких и швейцарских инженеров, Петр мог познакомиться с европейской наукой и культурой, а заодно удовлетворить свою страсть к фейерверкам и кораблям (в перерывах между бурными застольями и кутежами ночи напролет). В 1692-1693 годах на Плещеевом озере Петр сам построил военный корабль, от киля до мачт. В следующем 1694 году умерла его мать, и Петр стал полновластным государем.
В 1695-1696 годах этот необычный и необычной внешности человек — вдобавок к росту в 6 футов 7 дюймов он страдал нечастыми, но устрашающими лицевыми судорогами — напал на порт Азов на Черном море и отобрал его у турок-оттоманов. В 1697-1698 годах он инкогнито отправился во Францию, Британию и Голландию, став первым российским самодержцем, вообще выехавшим за границу; в ходе своего путешествия он учился. (По поводу его странствий в Британии хорошо известна — хотя и является, скорее всего, апокрифом — следующая история. Остановившись в сельском доме Джона Ивлина в пригороде Лондона, Петр однажды вошел в гостиную с мушкетом в руках и заявил на своем ломаном английском: «Я только что стрелял пейзан». — «Нет, нет, мой добрый друг, — со смехом ответил хозяин, — вы имеете в виду фазана». — «Nyet, — ответил Петр, качая головой, — Это быфф пейзан. Он быфф дерзкий, унт я стрелял его».) Вернувшись в Россию, Петр приступил к осуществлению целого ряда невиданных реформ, повелев боярам сбрить бороды, усмирив церковь и уничтожив старую московскую царскую гвардию — стрельцов, которые терроризировали его в детстве. В 1700 году он начал двадцатилетнюю войну со шведским королем Карлом; в 1703 году Петр вторгся на шведские земли и занял области вдоль Невы, от Ладожского озера до берегов Балтики. Там, на земле, которая все еще формально принадлежала могущественному и непобежденному врагу, в болотистой дельте Невы, он основал новую столицу, Санкт-Петербург.
Будучи одной из тех потрясающих личностей, существование которых опровергает взгляд на ход истории как на театр теней — бездушную пьесу, разыгрываемую обезличенными силами, — Петр продолжил реформы в сфере управления, дворянства, торговли, образования и даже повседневного одеяния своих подданных. Не все из этого заработало — другими словами, не все закрепилось; и не все достигло сумрачных, скрытых в лесах глубин этой обширной и древней страны; но нет сомнения, что положение, в котором Петр оставил Россию, было совсем не похоже на то, в котором он ее принял.
И, что имеет прямое отношение к теме данной книги, он превратил ее в место, гостеприимное для математиков и математики!
VI.
В январе 1724 года Петр издал указ об основании Академии наук в Санкт-Петербурге. В указе объяснялось, что в обычной ситуации академия наук, где ученые занимаются исследованиями и изобретениями для блага государства, отличается от университета, предназначение которого состоит в обучении молодых людей. Однако из-за острого недостатка образованных людей в России под управлением Санкт-Петербургской академии будут находиться еще университет и гимназия (т.е. учреждение для среднего образования). Предполагалось, что академия будет иметь также свои собственные обсерватории, лаборатории, мастерские, издательство, печатный цех и библиотеку. Петр ничего не делал наполовину.
Нехватка образования в России была и правда столь высока, что попросту не существовало россиян, способных стать членами академии. Более того, поскольку в России отсутствовало достаточное число начальных и средних школ, не было даже молодых россиян, в достаточной степени подготовленных для того, чтобы стать студентами в университете. Эти проблемы были решены путем импорта требуемого персонала. В Европе подобная практика была вполне распространенной. Первым директором Парижской академии наук, основанной за 60 лет до того, был голландский физик Кристиан Гюйгенс. Правда, Санкт-Петербург находился далеко от главных центров европейской культуры, а западноевропейцы все еще воспринимали Россию как страну темную и варварскую, и поэтому им следовало предложить очень привлекательные условия. Как бы то ни было, в конце концов колеса механизма закрутились, нехватка университетских студентов была компенсирована за счет импорта восьми немецких юношей. Санкт-Петербургская академия распахнула свои двери в августе 1725 года — слишком поздно для того, чтобы царь Петр мог председательствовать на церемонии: он умер за шесть месяцев до этого.
Среди иностранных ученых, присутствовавших на первом заседании Санкт-Петербургской академии наук, были два брата, Николай и Даниил Бернулли. Им было соответственно 30 и 25 лет — то были сыновья Иоганна Бернулли из швейцарского Базеля, того самого господина, с которым мы уже встречались в главе 1.iii в связи с гармоническим рядом. (Имелась целая династия математиков Бернулли; в описываемом поколении был и третий брат, который последовал примеру отца и стал профессором математики в Базельском университете и который «воплощал в себе математический гений своего родного города во второй половине XVIII столетия», как написано в «Словаре научных биографий».)
К несчастью, проведя менее года в Санкт-Петербурге, Николай Бернулли умер («от чахоточной лихорадки»), в результате чего в академии образовалась вакансия. Даниил Бернулли еще в Базеле был знаком с Леонардом Эйлером и сейчас же рекомендовал его. Эйлер был рад возможности занять академический пост в столь молодом возрасте и прибыл в Санкт-Петербург 17 мая 1727 года, через месяц после своего двадцатилетия.
По несчастливому стечению обстоятельств это произошло спустя десять дней после смерти императрицы Екатерины, жены Петра, которая наследовала ему на троне и которая продолжала воплощать в жизнь его план устройства академии. Для России наступали не лучшие времена. Пятнадцатилетний период между смертью Петра и воцарением его дочери Елизаветы был временем слабого, безвольного руководства, политики временщиков и периодических приступов ксенофобии. Все враждующие кланы содержали сети шпионов и доносчиков, и атмосфера в столице (каковой теперь являлся Санкт-Петербург) менялась с «плохо» на «очень плохо». В правление жестокой, коварной и сумасбродной императрицы Анны Иоанновны (1730–1740) Россия скатилась к одному из периодов государственного террора, к которому сама императрица испытывала особую склонность: в течение этого времени не прекращались суды по обвинению в измене, массовые казни и другие зверства. Этот период получил печальную известность под названием бироновщины, по имени фаворита Анны Иоанновны немца Эрнста Иоганна Бирона, на которого простые россияне возлагали всю вину.
Эйлер стойко выносил все это в течение 13 лет, с головой погрузившись в работу и твердо держась подальше от двора с его интригами. «Общая осмотрительность привила ему неистребимую привычку к работе», — пишет Э.Т. Белл, и это кажется разумным объяснением невероятной продуктивности Эйлера. Даже сейчас еще не закончено полное издание собрания его трудов. К настоящему моменту оно состоит из 29 томов по математике, 31 по механике и астрономии, 13 по физике и 8 томов переписки.
Но для друга Эйлера Даниила Бернулли, с которым они вместе поселились в первые годы жизни в Санкт-Петербурге, удушливая политическая атмосфера в послепетровской России оказалась слишком тяжелой. В 1733 году Даниил уехал обратно в Базель, а Эйлер возглавил кафедру математики в академии. Это позволило ему получать доход, достаточный для женитьбы. Его избранницей стала швейцарская девушка Екатерина Гзель, дочь художника, жившего в то время в Санкт-Петербурге.
В такой обстановке в 1735 году Эйлер и решил базельскую задачу, которую мы рассмотрим в следующей главе. Двумя годами позже в небольшом меморандуме о бесконечных рядах Эйлер получил результат, который я назвал Золотым Ключом и которому будет посвящена первая половина главы 7. Коротко говоря, Эйлер — одно из главных действующих лиц в нашем повествовании, однако это станет понятно немного позднее, по мере развертывания математической части истории.
VII.
К 1741 году Эйлер устал от окружавших его доносов и публичных экзекуций «изменников». На прусский трон к этому моменту взошел Фридрих Великий, уже приступивший к своему плану превращения прусского королевства (до 1700 года — всего лишь герцогства) в одно из наиболее могущественных государств в Европе. Он запланировал создание Академии наук в Берлине с целью заменить ею или с ее помощью вдохнуть новую жизнь в находившееся при смерти Научное общество этого города; он пригласил Эйлера — к этому моменту знаменитого по всей Европе — в качестве директора математического класса академии. Эйлер прибыл в Берлин 25 июля 1741 года, после месячного путешествия по морю и суше из Санкт-Петербурга. Мать Фридриха София-Доротея Английская (приходившаяся сестрой Георгу II) понравилась молодому Эйлеру (ему было всего 34 года), но не могла толком его разговорить. «Почему бы вам не побеседовать со мной?» — спросила она, на что Эйлер ответил: «Потому, мадам, что я приехал из страны, где тех, кто много говорит, отправляют на виселицу».
Но вообще-то Эйлеру полагалось заговорить. Это было частью плана по переселению его в Берлин. Фридрих желал видеть свой двор своего рода салоном, где блестящие люди обмениваются блестящими речами. Эйлер в самом деле был блестящим человеком, но, к сожалению, только в математике. Его высказывания на темы философии, литературы, религии, а также о событиях в мире, хотя и демонстрировали его хорошую информированность и здравый смысл, оставались довольно общими и невыразительными. Фридрих, кроме того, был эгоистом, любившим манипулировать людьми и хотя в принципе желал бы окружить себя гениями, в реальности же предпочитал посредственностей, которые ему льстили. Если не считать нескольких светил, таких как Вольтер и Эйлер, общий интеллектуальный уровень при дворе Фридриха, судя по всему, несколько недотягивал до выдающегося. В 1745-1747 годах Фридрих построил для себя летний дворец Сан-Суси в Потсдаме, в 20 милях от Берлина. (Эйлер помогал разработать систему водяных насосов для дворца.) Кто-то из гостей Сан-Суси спросил одного из наследных принцев: «Чем вы здесь занимаетесь?» Принц ответил: «Мы спрягаем глагол s'ennuyer». «S'ennuyer» означает «скучать». Языком двора Фридриха был французский — язык высшего общества по всей Европе.
Эйлер задержался в Берлине на 25 лет, пережив там все ужасы Семилетней войны, когда иностранные армии дважды занимали Берлин, а каждый десятый подданный Фридриха умер от голода, болезни или пули. К тому времени на российском престоле воцарилась вторая Екатерина — Екатерина Великая. (Занятно, что на протяжении двух третей XVIII века — 67 лет из 100 — Россия, одна из наиболее трудных в управлении стран, управлялась женщинами, и в целом весьма успешно). Екатерина выказывала все признаки просвещенного монарха, при этом твердо удерживая трон. Более того, она была немецкой принцессой, и не исключено, что Эйлер каким-то образом свел с ней знакомство при дворе Фридриха еще до того, как ее отправили в Санкт-Петербург, чтобы выдать замуж за внука Петра Великого. Так или иначе, Эйлер оставил жеманство и интриги Сан-Суси и снова занял свою должность в Санкт-Петербурге — должность, которая невероятным образом ждала его, оставаясь незанятой. Последние 17 лет своей жизни он провел в России, до конца сохраняя работоспособность, и умер в возрасте 76 лет, полный сил и энергии (если не считать оставившего его зрения), в одно мгновение, держа внука на коленях.
VIII.
В этом очерке о Леонарде Эйлере мне пришлось серьезно себя сдерживать, потому что по ряду причин Эйлер вводит в число наиболее любимых мною личностей в истории математики. Одна из причин — чтение его работ доставляет большое удовольствие. Эйлер всегда выражается коротко и ясно, без лишней суеты и без излишнего лоска, свойственного Гауссу. Эйлер писал преимущественно по-латыни, но это не препятствие для понимания его текстов, поскольку ему был присущ сдержанный и утилитарный стиль.
Кристально ясная латынь Эйлера позволяет осознать, чего же лишилась западная цивилизация, когда ученые перестали писать на этом языке. Гаусс был последним из крупных математиков, кто придерживался латыни; ее забвение было одним из тех сдвигов, что принесли с собой Наполеоновские войны. Любопытно, что, хотя Венский конгресс, которым было отмечено окончание этих войн, представлял собой собрание реакционеров, намеревающихся восстановить в Европе status quo ante («как было прежде»), на самом деле эти войны до такой степени изменили все, что ничто после них не могло уже оставаться прежним. Историк Пол Джонсон написал об этом хорошую книгу «Рождение современности».
Другая причина, по которой меня привлекает фигура Эйлера, состоит в том, что он не гонялся за внешним блеском, не обладал какой-либо эксцентричной или курьезной чертой, а просто являл собой пример превосходного человека. Читая о его жизни, проникаешься его спокойной уверенностью в себе и внутренней силой. Эйлер ослеп на правый глаз, когда ему едва было 30 лет (бессердечный Фридрих называл его «мой Циклоп») и окончательно лишился зрения после шестидесяти. Похоже, что ни частичная, ни полная инвалидность не согнули его ни на йоту. Из его тринадцати детей лишь пятеро дожили до взрослого возраста и только трое пережили его. Его жена Екатерина умерла, когда Эйлеру было 69 лет; через год он женился во второй раз — тоже на девице по фамилии Гзель, сводной сестре Екатерины.
Он любил детей и, говорят, мог заниматься серьезными вычислениями в то время, как дети играли у его ног. (На меня как писателя, работающего дома в окружении двух маленьких детей, это производит действительно немалое впечатление.) По-видимому, он был не способен к интригам, никогда не терял друзей иначе как по причине смерти и был честен во всех своих начинаниях — хотя, если верить Стрэчи, готов был слегка поступиться принципами ради спокойной жизни! Он написал один из первых научно-популярных бестселлеров «Письма к немецкой принцессе», где объяснял обычным читателям, почему небо голубое, почему луна кажется больше, когда она восходит, а также рассматривал другие подобные вопросы, занимающие умы.
В основе всего этого лежала твердая как гранит религиозная вера. Эйлер рос кальвинистом и всегда был привержен этой вере. Его отец, как и отец Римана, был пастором в деревенской церкви, и Эйлеру, как и Риману, изначально предназначалась церковная карьера. Сообщают, что во время жизни в Берлине «он каждый вечер собирал всю семью целиком и читал главу из Библии, сопровождая чтение проповедью». И это происходило ровно тогда, когда при дворе, согласно Маколею, «главнейшие темы разговоров вертелись вокруг нелепости религиозных убеждений любого толка». Трудолюбивый, благочестивый, стоический, преданный своей семье, живущий в простоте и просто изъясняющийся — неудивительно, что Фридрих его недолюбливал. Но настало время перейти от дней к трудам и взглянуть на первый великий триумф Эйлера — базельскую задачу.

