Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 13. Муравей Арг и муравей Знач
Дальше: Глава 15. О большое и мебиусово мю
Глава 14. Во власти одержимости
I.
Геттинген, конечно, был не единственным местом на земле, где в первые годы XX века создавалась первоклассная математика. Взглянем на английского математика Джона Идензора Литлвуда за шестьдесят с чем-то лет до того, как он предлагал «понюхать пороху» Хью Монтгомери. В 1907 году, будучи молодым математиком в Тринити-колледже в Кембридже, Литлвуд был занят поиском содержательной задачи, из которой удалось бы вырвать хороший «кусок мяса» для диссертации.
Барнс решился предложить такую новую задачу: «Доказать Гипотезу Римана». В конце концов оказалось, что это героическое предложение привело к некоторым результатам; но сначала надо сказать о ситуации с ζ(s) и с простыми числами на 1907 год, в особенности в том плане, как я ее воспринимал. Я впервые познакомился с ζ(s) у Линделёфа, но там вообще ничего не говорится о простых числах, а я и не догадывался о существовании какой бы то ни было связи между ними. Я знал, что ГР — знаменитая гипотеза, но полагал, что это просто проблема из теории целых функций. А все это происходило в течение долгих каникул, когда у меня не было доступа к литературе (даже если бы мне пришло в голову заняться какими-нибудь поисками). (Что касается людей образованных лучше меня, то лишь некоторые слышали о работе Адамара и лишь совсем немногие — о статье де ля Валле Пуссена в каком-то бельгийском журнале. Во всяком случае, та деятельность воспринималась как очень сложная и проходящая в стороне от основного течения математики. Знаменитая статья Римана была включена в собрание его трудов; в ней утверждается ГР и потрясающая, но не доказанная формула для π(x). Сама Теорема о распределении простых чисел не упоминается, хотя ее ничего не стоит получить, если принять приведенную там формулу. Что же касается Харди, то, как он впоследствии сказал мне, он знал, что ТРПЧ была доказана, но, правда, думал, что это сделал Риман. Все изменилось в мгновение ока с выходом в свет книги Ландау в 1909 году.)
Это отрывок из «Математической смеси» Литлвуда — причудливого собрания мемуарных фрагментов, шуток и математических головоломок, впервые опубликованного в 1953 году. Кроме самого Литлвуда, действующие лица в приведенном отрывке — это английский математик Годфри Хэролд Харди (1877-1947) и немец Эдмунд Ландау (1877-1938). Эти трое — Ландау, Харди, Литлвуд — через полпоколения после Гильберта были пионерами в ранних попытках одолеть Гипотезу Римана.
II.
Британская математика в XIX столетии демонстрировала странную асимметрию в своем развитии и достижениях. Британские ученые добились значительных успехов в наименее абстрактных областях математики — тех, которые ближе всего связаны с физикой. Такое наблюдение — результат моего высшего математического образования, полученного в Лондоне. Когда у нас были занятия по вещественному анализу, теории функций комплексной переменной, теории чисел и алгебре, фамилии ученых в названиях теорем сыпались на нас с той стороны Ла-Манша: Коши, Адамар, Якоби, Чебышев, Риман, Эрмит, Банах, Гильберт… А потом мы шли на лекции по ММФ (т.е. по методам математической физики) и внезапно снова оказывались на Британских островах викторианской эпохи: теорема Грина (1828), формула Стокса (1842), число Рейнольдса (1883), уравнения Максвелла (1855), оператор Гамильтона (1834)…
Кроме того, заметной активностью отличались британские ученые, занятые в наиболее абстрактных областях математики: Артур Кэли и Дж. Дж. Сильвестр изобрели матрицы (о них мы еще поговорим ниже) и теорию алгебраических инвариантов. Джордж Буль открыл целый новый материк «оснований» — математической логики, которую он называл «законами мышления». (Можно поспорить по поводу того, действительно ли этот предмет находится так уж далеко по шкале абстракции; сам Буль заявлял, что его намерением было сделать логику частью прикладной математики. Однако мне кажется, что математическая логика достаточно абстрактна для большинства из нас, простых смертных.) Любопытно отметить, что за неделю до того, как Гильберт выступил на Парижском конгрессе, тот же актовый зал Сорбонны был зарезервирован для Международного философского конгресса. Один из прочитанных там докладов назывался «Представления о порядке и абсолютном положении в пространстве и времени». Докладчиком был молодой английский логик, также из Тринити-колледжа, по имени Бертран Рассел, который спустя 10 лет вместе с Элфредом Нортом Уайтхедом стал автором классического трактата по математической логике (точнее, логифицированной математике) — Principia Mathematica.
Таким образом, в Британии полным ходом развивалась наименее абстрактная и наиболее абстрактная математика, а огромное количество всего, требующего среднего уровня абстракции, — теория функций, теория чисел, большая часть алгебры — было оставлено для континентальной Европы. В анализе — наиболее плодородном разделе математики XIX века — присутствие британцев практически незаметно. К концу столетия они фактически исчезли даже из тех областей, где традиционно были сильно представлены. Лишь семь британских математиков присутствовали на Парижском конгрессе; по этому показателю Британия стояла ниже Франции (90), Германии (25), США (17), Италии (15), Бельгии (13), России (9), Австрии и Швейцарии (по 8 каждая). В плане математики Британия в 1900-х годах была тихой заводью.
Но и в тихой заводи, как известно, черти водятся. Тринити-колледж в Кембридже, где обитал Литлвуд, поддерживал сильную математическую традицию. Некогда здесь работал сэр Исаак Ньютон (1661-1693), и колледж мог похвастаться тем, что в течение XIX столетия выпустил из своих стен нескольких гениев от математики и физики: это Чарльз Бэббидж, которого обычно считают изобретателем компьютера; астроном Джордж Эйри, именем которого названо семейство математических функций; логик Огастес де Морган; алгебраист Артур Кэли; Джеймс Клерк Максвелл и другие, несколько менее известные имена. Бертран Рассел защитил диссертацию в Тринити-колледже в 1893 году, стал сотрудником в 1895-м и продолжал преподавать там в то время, когда сотрудником стал и Харди. История Тринити-колледжа в XX столетии оказалась несколько менее однородной. Отсюда происходили основные участники кембриджской шпионской сети а также несколько блумсберийцев. Однако в том, что касается математики в первые годы столетия, Тринити-колледж был прежде всего местом, где работал Г.X. Харди — тот самый Харди из воспоминаний Литлвуда. Именно Харди, как никто другой, пробудил английскую чистую математику от долгого сна.
Когда в 1897 году Харди трудился в Тринити-колледже над диссертацией, на глаза ему попался знаменитый в то время учебник Cours d'Analyse написанный французским математиком Камилем Жорданом. Жордан известен тем, кто изучает теорию функций комплексной переменной, поскольку в ней есть теорема Жордана, утверждающая примерно следующее: несамопересекающаяся замкнутая плоская кривая (например, окружность) разбивает плоскость на две части: внутреннюю и внешнюю. Эту теорему необычайно трудно доказать — Эстерман говорит о собственном доказательстве Жордана как об «интеллектуальном подвиге». По-видимому, Cours d'Analyse произвел на Харди примерно такое же впечатление, какое Гомер в переводе Чапмена произвел на Китса.
После того как Харди приняли в Тринити-колледж (в то самое лето, когда Гильберт выступал со своей речью), он посвятил несколько последующих годов написанию работ по анализу.
Одним из плодов раннего увлечения Харди анализом стал учебник для студентов, называвшийся «Курс чистой математики», впервые вышедший в 1908 году и с тех пор никогда не перестававший издаваться. Как и большинство британских студентов XX века, я учил анализ по этой книге. Мы называли ее просто «Харди». Заглавие книги в сильной степени вводит в заблуждение, потому что там на самом деле нет ничего, кроме анализа, — никакой алгебры, никакой теории чисел, никакой геометрии, никакой топологии. Правда, никто не обращал на это внимания. В качестве введения в классический (т.е. в рамках XIX века) анализ этот учебник близок к идеалу настолько, насколько это вообще возможно для учебника. Его влияние на мой собственный подход к математике оказалось огромным. Когда я смотрю на то, что уже написано в этой книге, я явственно вижу Харди.
III.
Г.X. Харди был чудаком такого рода, который только Англия XIX века могла породить. В старости он написал довольно занятную книгу под названием «Апология математика» (1940), в которой описал свою жизнь как математика. В некоторых отношениях это печальная, точнее, элегическая книга. Причину этого прекрасно выразил Ч.П. Сноу в своем предисловии к последующим изданиям. Харди был Питером Пэном — мальчиком, который так и не вырос. По словам Сноу, «до старости жизнь его оставалась жизнью блестящего молодого человека. Таким же оставался и его дух — его игры, его интересы поддерживали легкость молодого дона. И, как и у многих людей, которые сохраняют интересы своей молодости до седьмого десятка, его последние годы были из-за этого не очень веселыми». А вот что пишет Литлвуд: «До тридцатилетнего возраста он выглядел невероятно молодым». Харди играл в крикет, к которому питал настоящую страсть, а также в теннис на закрытом корте (известный также как real (royal) tennis или jeu de paume) — игру более трудную, требующую большего интеллекта, чем обычный теннис.
В течение 12 лет, с 1919 по 1931 год, Харди возглавлял кафедру в Оксфорде. На 1928-29 академический год он уезжал в Принстон, а остальную часть своей жизни провел в Тринити-колледже в Кембридже. Приятный и обходительный, он никогда не был женат и, насколько известно, не имел никаких близких привязанностей какого бы то ни было сорта. Следует помнить, что в те времена колледжи в Оксфорде и Кембридже были учреждениями только для мужчин, с сильным оттенком женоненавистничества. До 1882 года сотрудникам Тринити-колледжа не разрешалось жениться. Недавно, вполне в духе нашего времени, высказывались предположения о гомосексуальности Харди. Я отошлю любознательного читателя к написанной Робертом Канигелом биографии Сринивасы Рамануджана, которому Харди оказывал поддержку, — «Человек, который знал, что такое бесконечность»; там эта тема обсуждается более подробно. Ответ представляется таким: скорее всего нет, разве только в самых сокровенных мыслях.
Историй о Харди даже больше, чем историй о Гильберте — одну из них, как я понимаю, я уже рассказал. Вот две другие, причем в каждой из них присутствует Гипотеза Римана. Первая взята из его некролога в британском научном журнале Nature.
У Харди была одна главенствующая страсть — математика. Помимо этого его основными интересами были игры в мяч, в которых он был опытным игроком и искушенным экспертом. Его пристрастия и антипатии иллюстрируются списком из «шести новогодних пожеланий», который он открыткой отправил другу (в 1920-х годах):1) доказать Гипотезу Римана;2) в четвертом иннинге последнего Тест-матча на «Овале» сделать 211 пробежек, пока не выбит никто из игроков своей команды.3) найти доказательство несуществования Бога, способное убедить широкую общественность;4) оказаться первым человеком на вершине Эвереста;5) быть провозглашенным первым президентом Союза Советских Социалистических Республик Великобритании и Германии;6) убить Муссолини.
Третий пункт иллюстрирует другую сторону присущей Харди эксцентричности. Хотя он и утверждал, что не верит в Бога, он вечно состязался с Ним в остроумии. В 1930-х годах Харди часто ездил к своему другу Харальду Бору (младшему брату физика Нильса Бора), который был профессором математики в Копенгагенском университете. Про одно из таких путешествий Джордж Пойа рассказывает следующую историю.
Харди оставался в Дании у Боров до самого конца летних каникул, а когда ему наконец пришлось возвращаться в Англию и приступать там к чтению лекций, для путешествия нашлось лишь одно довольно утлое судно <…> Северное море может быть достаточно суровым, и вероятность того, что такое маленькое судно потонет, не была строго равной нулю. Как бы то ни было, Харди сел на этот корабль, но послал Бору открытку: «Я доказал Гипотезу Римана. Г.X. Харди». Если корабль потерпит бедствие и Харди утонет, то все будут думать, что он сумел доказать Гипотезу Римана. Однако Господь не допустит, чтобы Харди досталась такая слава, а потому Он сделает так, чтобы корабль не затонул.
Помимо своего замечательного учебника Харди знаменит более всего благодаря своему участию в двух прославленных научных тандемах. Широкую известность получила его совместная работа с Рамануджаном, что и справедливо, поскольку эта фабула — одна из наиболее любопытных и волнующих во всей истории математики. Она полностью изложена в упоминавшейся уже книге Роберта Канигела. Однако сотрудничество Харди и Рамануджана имеет только очень косвенное отношение к истории Гипотезы Римана, так что ничего больше говорить о нем я не буду.
Другим знаменитым научным тандемом, в котором участвовал Харди, была совместная работа с Литлвудом, с воспоминаний которого о его собственных аспирантских исследованиях и начинается данная глава. Литлвуда приняли в число преподавателей Тринити-колледжа в 1910 году. Его сотрудничество с Харди началось в том же году и продолжалось до 1946 года. В те годы, когда Харди был в Оксфорде и Принстоне, а также во время Первой мировой войны, когда Литлвуд выполнял работы для нужд британской артиллерии, их совместная работа в основном проходила по переписке. Однако такой способ общения нисколько их не затруднял: они нередко обменивались письмами и в то время, когда оба проживали в своих квартирах в Тринити-колледже.
И Харди, и Литлвуд были великими математиками; оба были сыновьями школьных учителей и оба на всю жизнь остались холостяками. Практически во всем остальном они были совершенно не похожи. Харди обладал определенными странностями. Например, он ненавидел, когда его фотографируют, — сохранилось не больше десятка его фотографий, а когда он останавливался в гостинице или в квартирах для приезжих профессоров, завешивал там все зеркала. Литлвуд же был человеком куда менее притязательным. Харди был стройного и худощавого телосложения, а Литлвуд — крепким и коренастым и при этом прекрасным спортсменом во всех дисциплинах — в плавании, гребле, скалолазании, крикете. До 39 лет он продолжал кататься на лыжах и добился в этом занятии высокой степени профессионализма, что для англичанина в то время было весьма необычным. Литлвуд любил музыку и танцы.
Несмотря на свое соответствие традиционному представлению о сотруднике колледжа — он не был женат и жил в одной и той же квартире в Тринити-колледже в течение 65 лет, с 1912 по 1977 год, — у Литлвуда было по крайней мере двое детей. Как рассказывает его коллега Бела Боллобаш, в свои молодые годы Литлвуд обычно раз в год ездил в отпуск в Корнуолл, где останавливался в семье доктора. Дети в этой семье выросли, называя его «дядя Джон». Об одной из девочек — ее звали Энн — Литлвуд говорил как о своей племяннице. Но когда Литлвуд сделался близким другом семьи Боллобаш, он признался, что Энн была на самом деле его дочерью. Боллобаш с женой стали убеждать его, чтобы он перестал называть ее племянницей и начал говорить «моя дочь». Однажды вечером в профессорской он так и сделал — и испытал немалое разочарование, когда никто из его коллег не выказал ни малейшего удивления. Позднее, после смерти Литлвуда в 1977 году, в Тринити-колледже появился мужчина средних лет, интересовавшийся личными вещами покойного, объясняя при этом, что он его сын.
IV.
В 1910-х и и 1920-х годах сочетание «Харди и Литлвуд» стало настолько часто встречаться в качестве авторов математических статей, что ходили шутки, будто Литлвуд был вымышленной фигурой, которую придумал Харди, чтобы сваливать на него все ошибки. Говорят, что один немецкий математик пересек Ла-Манш только лишь для того, чтобы утвердиться в своем убеждении, что Литлвуда не существует.
Этим математиком был Эдмунд Ландау; он был на семь дней младше Харди. Ландау был феноменом, который встречается не так часто: выходец из богатой семьи, он тем не менее выбрал совершенно не прибыльную сферу деятельности и добился в ней больших успехов — придерживаясь при этом высочайших стандартов трудовой этики. Его мать Йоханна, урожденная Якоби, происходила из богатой семьи банкиров, а отец был успешным профессором гинекологии в Берлине, имевшим прекрасную практику. Кроме того, Ландау-старший активно поддерживал идеи еврейского движения. Их дом располагался в наиболее фешенебельном берлинском квартале по адресу Pariser Platz 6а, недалеко от Бранденбургских ворот. Эдмунд Ландау стал профессором в Геттингене в 1909 году. Когда люди спрашивали, как найти дорогу к его дому, он отвечал: «Вы его не пропустите. Это самый элегантный дом в городе». Как и отец (и как Жак Адамар), он проявлял интерес к сионизму, способствовал организации Еврейского университета в Иерусалиме и прочитал там (на иврите) первую лекцию по математике вскоре после открытия университета в апреле 1925 года.
Ландау был незаурядной личностью — а это было великое время для незаурядных личностей от математики, — и апокрифов о нем имеется не меньше, чем о Гильберте и Харди. Наверное, самый известный анекдот — его замечание об Эмми Нетер, которая была его коллегой по Геттингену. Нетер была мужеподобна манерами и фигурой. Когда Ландау спросили, не являет ли она собой пример великого математика-женщины, он ответил: «Я твердо заявляю, что Эмми — великий математик; но насчет женственности не поручусь». Его трудовая дисциплина вошла в легенду. Рассказывают, что, когда один из его ассистентов лежал в больнице, поправляясь после серьезной болезни, Ландау забрался по лестнице к окну, которое вело к несчастному, и пропихнул через него толстенную папку с работой. Литлвуд говорил о нем: «Он просто не знал, что такое чувствовать себя усталым». Харди добавляет, что Ландау работал каждый день с семи утра до полуночи.
Ландау был одаренным и увлеченным преподавателем и необычайно продуктивным математиком. Он написал более 250 статей и 7 книг. Его роль в нашей истории определяется первой из них — классическим трудом по теории чисел, опубликованным в 1909 году. Это та книга, о которой говорит Литлвуд в отрывке, приведенном в самом начале этой главы: «Все изменилось в мгновение ока с выходом в свет книги Ландау…» Полное название книги было Handbuch der Lehre van der Verteilung der Primzahlen — «Учебник по теории распределения простых чисел». Теоретико-числовики обычно называют ее просто Handbuch. В двух томах этой книги, каждый из которых состоит более чем из 500 страниц, собрано все, что было в тот момент известно о распределении простых чисел; изложение построено с сильным акцентом в сторону аналитической теории чисел. Гипотеза Римана сформулирована на странице 33. Handbuch была не первой книгой по аналитической теории чисел — Пауль Бахманн опубликовал такую книгу в 1894 году, — однако очень подробное и систематическое изложение в книге Ландау сделало весь предмет более ясным и привлекательным, и эта книга немедленно стала стандартом в этой области.
Мне кажется, что Handbuch Ландау не переводился на английский. Специалист по теории чисел Хью Монтгомери (он будет главным действующим лицом в главе 18) выучил немецкий по мере того, как трудился над чтением Handbuch, держа один палец на раскрытом словаре. Он рассказывает следующее. Первые 50 с чем-то страниц посвящены историческому обзору, разбитому на разделы, каждый из которых озаглавлен по имени великого математика, внесшего главный вклад в данную область: Эвклид, Лежандр, Дирихле и т.д. Последние четыре раздела озаглавлены Hadamard, Von Mangoldt, De la Vallée Poussin, Verfasser. На Хью произвел большое впечатление вклад, который внес в науку Verfasser, но он недоумевал, почему же раньше ему не приходились слышать об этом замечательном математике. Лишь некоторое время спустя он узнал, что Verfasser по-немецки означает «автор» (обычные существительные в немецком пишутся с заглавной буквы).
V.
«Все изменилось в мгновение ока с выходом в свет книги Ландау…» И Харди, и Литлвуд наверняка прочитали ее, как только она вышла. Вот слова Харди из некролога Ландау, написанного им (совместно с Хансом Хайльбронном) для Лондонского математического общества:
Handbuch, вероятно, была самой важной из написанных им книг. В ней аналитическая теория чисел впервые представлена не как собрание нескольких прекрасных разрозненных теорем, а как систематическая наука. Появление этой книги изменило сам предмет, до того представлявший собой нетронутый уголок для нескольких безрассудных смельчаков, превратив его в плодороднейшее поле для исследований, каким он и оставался в течение прошедших с тех пор трех десятилетий. Почти по всем рассматриваемым там вопросам сейчас получено новое знание, в силу чего написанное в книге устарело, и в этом-то и состоит ее величайшая роль.
Без сомнения, именно из Handbuch и Харди, и Литлвуд заразились навязчивой идеей Гипотезы Римана. Первые плоды последовали в 1914 году, но не в виде совместной работы, хотя они и сотрудничали в то время, а в виде двух отдельных статей, каждая из которых сыграла значительную роль.
Статья Харди под названием Sur lez zéros de la fonction ζ(s) de Riemann вышла в Comptes Rendus Парижской академии наук. В ней он доказал первый важный результат о распределении нетривиальных нулей.
Результат Харди 1914 года
Бесконечно много нетривиальных нулей дзета-функции удовлетворяют Гипотезе Римана (т.е. имеют вещественную часть одна вторая).
Хотя это и был значительный шаг вперед, для читателя важно понимать, что это не решило вопроса с Гипотезой. Имеется бесконечно много нетривиальных нулей; Харди доказал, что бесконечно много из них имеют вещественную часть одна вторая. Тем самым остаются открытыми три возможности.
• Бесконечно много нулей не имеют вещественную часть одна вторая.
• Лишь конечное число нулей не имеет вещественной части одна вторая.
• Нет нулей, вещественная часть которых не равна одной второй, — утверждение Гипотезы!
Чтобы провести аналогию, рассмотрим следующие утверждения о четных числах, превосходящих двойку, т.е. 4, 6, 8, 10, 12, …
• Бесконечно много этих чисел делится на 3; бесконечно много не делится.
• Бесконечно много из них больше чем 11; только четыре числа не больше.
• Бесконечно много из них представимы в виде суммы двух простых; нет таких, которые не представимы — гипотеза Гольдбаха (которая все еще не доказана на момент написания книги).
Статья Литлвуда, также опубликованная в Comptes Rendus Парижской академии наук в том же году, называлась Sur la distribution des nombres premiers. В ней доказан результат столь же тонкий и столь же замечательный, как результат Харди, хотя и относящийся к несколько другому направлению исследований в данной области. Обсуждение этого результата требует небольшой преамбулы.
VI.
Мы уже отмечали, что в начале XX века наблюдалось следующее общее направление мыслей по поводу Гипотезы Римана. Теорема о распределении простых чисел (ТРПЧ) была доказана. С математической точностью было установлено, что действительно π(x) ~ Li(x) — или, словами, что относительная разность между π(x) и Li(x) уменьшается до нуля по мере того, как x делается все больше и больше. Так что же тогда можно утверждать об этой разности — т.е. об остаточном члене? Именно при внимательном рассмотрении остаточного члена математики обратили свои взоры к Гипотезе Римана, поскольку в работе Римана 1859 года для остаточного члена было приведено точное выражение. Как будет показано в должном месте, это выражение включает в себя все нетривиальные нули дзета-функции, так что ключ к пониманию остаточного члена каким-то образом скрыт среди этих нулей.
Чтобы говорить более конкретно, я приведу некоторые реальные значения остаточного члена. В таблице 14.1 «абсолютн.» означает разность Li(x) − π(x), а «относит.» означает это же число, отнесенное к (т.е. деленное на) π(x).
Таблица 14.1.
Мы видим, что относительная ошибка, без сомнения, уменьшается, стремясь к нулю, как ей и предписывает ТРПЧ. Это происходит потому что, хотя абсолютная ошибка тоже растет, она делает это далеко не так быстро, как π(x).
Пытливый математический ум сейчас спросит: «А как именно ведут себя эти два числа?» Имеются ли правила, описывающие медленный рост абсолютной ошибки или стремление относительной ошибки к нулю? Другими словами, если выкинуть из таблицы вторую и четвертую колонки и рассмотреть получившуюся двухколоночную таблицу как «моментальный снимок» некоторой функции (колонки аргумент-значение), то что это будет за функция? Можно ли для нее получить формулу с волнами, как это было сделано для π(x)?
Здесь-то на сцене и появляются нетривиальные нули дзета-функции. Они тесно связаны (способом, который мы рассмотрим ниже во всех математических подробностях) с остаточным членом.
Хотя в ТРПЧ говорится об относительной ошибке, исследования в этой области в большей степени имеют дело с абсолютной ошибкой. На самом деле неважно, какую из них рассматривать. Относительная ошибка есть просто абсолютная ошибка, деленная на π(x), так что в любой момент несложно перейти от одной к другой. Итак, можно ли получить какие-нибудь результаты об абсолютном остаточном члене Li(x) − π(x)?
VII.
Взглянув на рисунок и таблицу , можно с достаточной уверенностью заключить, что абсолютная разность Li(x) − π(x) положительна и возрастает. Численные свидетельства в пользу этого так убедительны, что Гаусс в своих собственных исследованиях полагал, что всегда так и происходит. Весьма вероятно, что исследователи поначалу соглашались с тем, или, по крайней мере, чувствовали уверенность в том, что π(x) всегда меньше чем Li(x). (Относительно мнения Римана по этому поводу ясности нет.) Поэтому статья Литлвуда 1914 года оказалась сенсацией, ибо в ней было установлено, что, напротив, существуют такие числа x, что π(x) больше чем Li(x). На самом деле доказано было гораздо большее.
Результат Литлвуда 1914 года
Разность Li(x) − π(x) изменяется от положительной к отрицательной и обратно бесконечно много раз.
Если учесть, что π(x) меньше, чем Li(x), для всех x, до которых смогли добраться даже самые мощные компьютеры, то где же находится первая точка перехода, первое «литлвудово нарушение», когда π(x) становится равной, а затем и превосходит Li(x)?
В подобных ситуациях математики отправляются на поиски того, что они называют верхней границей, — такого числа N, для которого можно доказать, что, каким бы ни был точный ответ на данный вопрос, он во всяком случае будет меньше, чем N. Установленные верхние границы такого рода нередко оказываются много больше, чем реальный ответ.
Так и обстояло дело с первой установленной верхней границей литлвудова нарушения. В 1933 году студент Литлвуда Сэмюель Скьюз показал, что если Гипотеза Римана верна, то переход должен наступать раньше, чем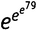 
, что представляет собой число из примерно 10десять миллиардов триллионов триллионов цифр. Это не само число — это число цифр в том числе. (Для сравнения заметим, что общее количество всех атомов во Вселенной оценивается числом из примерно восьмидесяти цифр.) Этот монстр получил известность как «число Скьюза» — самое большое число, которое когда-либо до того следовало из математического доказательства.
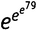, что представляет собой число из примерно 10десять миллиардов триллионов триллионов цифр. Это не само число — это число цифр в том числе. (Для сравнения заметим, что общее количество всех атомов во Вселенной оценивается числом из примерно восьмидесяти цифр.) Этот монстр получил известность как «число Скьюза» — самое большое число, которое когда-либо до того следовало из математического доказательства.В 1955 году Скьюз улучшил свой результат, на этот раз даже не предполагая справедливости Гипотезы Римана, и оказалось, что новое число содержит 10одна тысяча цифр. В 1966 году Шерман Леман сумел понизить верхнюю границу до куда более разумного (по крайней мере, позволяющего себя записать) числа 1,165×101165 (числа, другими словами, из каких-то 1166 цифр), а потом еще сильнее, до 6,658×10370.
На момент написания книги (середина 2002 года) лучшее достижение принадлежит Картеру Бейсу и Ричарду Хадсону, которые также исходили из теоремы Лемана. Они показали, что имеются литлвудовы нарушения в окрестности числа 1,39822×10316, а также привели некоторые аргументы в пользу того, что это нарушение может оказаться первым. (Статья Бейса и Хадсона оставляет открытой маленькую лазейку для существования нарушений на более малых высотах, возможно, даже на столь низкой высоте, как 10176. Они также установили существование грандиозной зоны нарушений вблизи числа 1,617×109608.)
VIII.
Колебания остаточного члена Li(x) − π(x) от положительных к отрицательным значениям и затем обратно происходящем не менее в пределах вполне определенных ограничений. Иначе не выполнялась бы ТРПЧ. Некоторые соображения по поводу природы этих ограничений возникли еще в результате усилий, направленных на доказательство ТРПЧ. Де ля Валле Пуссен включил в свое доказательство ТРПЧ некоторую оценку для функции, выражающей это ограничение. Пять лет спустя шведский математик Хельге фон Кох доказал следующий ключевой результат, который я сформулирую в его современной записи.
Результат фон Коха 1901 года
Если Гипотеза Римана верна, тоπ(x) = Li(x) + Ο(√x∙ln x).
Уравнение здесь читается так: «Пи от икс равно интегральному логарифму от икс плюс Ο большое от корня из икс, умноженного на логарифм икс». Теперь надо объяснить, что же такое «О большое».
