Книга: Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
Назад: Глава 14. Во власти одержимости
Дальше: Глава 16. Вверх по критической прямой
Глава 15. О большое и мебиусово мю
I.
Эта глава посвящена двум математическим темам, которые связаны с Гипотезой Римана, но помимо этого друг с другом никак не связаны. Эти темы — «Ο большое» и мю-функция Мебиуса. Рассмотрим сначала Ο большое.
II.
Когда Пауль Туран — великий венгерский математик, занимавшийся теорией чисел, — умирал от рака в 1976 году, его жена находилась у его постели. Она сообщила, что его последние слова были «Ο большое от единицы». Математики передают эту историю с благоговением: «Заниматься теорией чисел до самого конца! Истинный математик!»
Ο большое пришло в математику из книги Ландау 1909 года, влияние которой, как я уже рассказывал, было поистине огромным. Ландау на самом деле не изобрел Ο большое. Он чистосердечно признается на странице 883 своего Handbuch, что позаимствовал его из трактата Пауля Бахманна 1894 года. Поэтому довольно несправедливо называть его «ландаувским О большим» равно как несправедливо и то, что многие математики, по-видимому, полагают, что именно Ландау его изобрел. Ο большое присутствует повсеместно в аналитической теории чисел и даже просочилось оттуда в другие области математики.
Ο большое — это способ наложить ограничение на величину функции, когда аргумент устремляется к (как правило) бесконечности.
Определение Ο большого
Функция A есть Ο большое от функции B, если для достаточно больших аргументов величина A никогда не превосходит некоторого фиксированного кратного величины B.
Вслед за Паулем Тураном рассмотрим Ο большое от единицы. «Единица» здесь понимается как функция, причем функция простейшего вида. Ее график — горизонтальная прямая, проходящая на высоте 1 над горизонтальной осью. Для вообще любых аргументов значение этой функции равно… просто 1. Ну и что же тогда означает, что функция f(x) есть Ο большое от единицы? По только что данному определению это означает, что, когда аргумент x уходит на бесконечность, f(x) никогда не превзойдет некоторого фиксированного кратного 1 — другими словами, график функции f(x) навсегда останется ниже некоторой горизонтальной прямой. Это полезная информация о данной нам функции f(x). Существует множество функций, для которых это не так. Это не так, например, для x2 и для x в любой положительной степени, ни для ex ни даже для ln x.
На самом деле Ο большое означает еще кое-что, кроме этого. Заметим, что в определении сказано «величина A». Это означает «значение A без учета знака». Величина числа 100 есть 100; величина числа −100 есть также 100. Ο большое не принимает в расчет знак минус. Сказать, что некоторая функция f(x) есть Ο большое от единицы, означает сказать, что f(x) навсегда заключена между двумя горизонтальными прямыми, одна из которых проходит выше горизонтальной оси, а другая проходит на таком же расстоянии ниже.
Как уже говорилось, очень многие функции не являются Ο большим от единицы. Простейшая из них — это функция x, то есть функция, значения которой всегда равны ее аргументу. Ее график — диагональная прямая, покидающая рисунок в верхнем правом углу. Ясно, что она не заключена между какими бы то ни было горизонтальными прямыми. Вне зависимости оттого, сколь широко вы расположите эти горизонтальные прямые, функциях рано или поздно вырвется за их пределы. Это останется верным, если уменьшить наклон. Функции 0,1x (показана на рисунке 15.1), 0,01x, 0,001x и 0,0001x все в конце концов прорвутся через любые горизонтальные прямые, которые вы установите в качестве ограничения. Ни одна из них не является Ο большим от единицы.
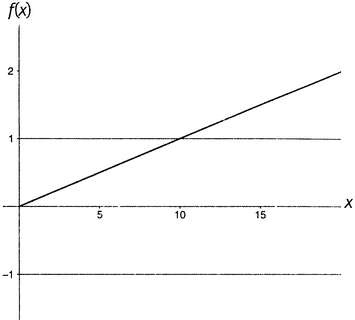
Рисунок 15.1. Функция 0,1x не есть Ο большое от единицы.
Этим иллюстрируется и еще один аспект Ο большого. Ο большое игнорирует не только знаки, но и множители. Если A есть Ο большое от B, то таковыми же будут 10A, 100A и 1000 000A; таковыми будут и одна десятая A одна сотая A одна миллионная A. Ο большое не сообщает нам о точном темпе роста — для этого у нас есть производные. Она сообщает о типе роста. Функция «единица» вообще не имеет никакого темпа роста — она намертво постоянная. Функция, являющаяся Ο большим от единицы, никогда не возрастет быстрее этого. Она может выделывать всякое другое: прижиматься к нулю, колебаться без конца внутри ограничивающих ее прямых или же подходить к одной из ограничительных линий все ближе и ближе, но она никогда не взовьется внезапно вверх и не нырнет внезапно вниз, прорываясь через эти линии и оставаясь после этого снаружи.
Приведенные функции 0,1x, 0,01x, 0,001x и 0,0001x — не Ο большое от единицы; все они — Ο большое от x. Такова же и любая другая функция, которая остается навсегда заключенной в «куске пиццы» между прямой ax и ее зеркальным отражением −ax. На рисунке 15.2 приведен пример функции, которая не остается в таких пределах. Это 0,1x2 — квадратичная функция. Не важно, сколь широким вы сделаете этот кусок пиццы — т.е. не важно, сколь велико значение a, — график функции 0,1x2 рано или поздно прорвется через верхнюю границу.
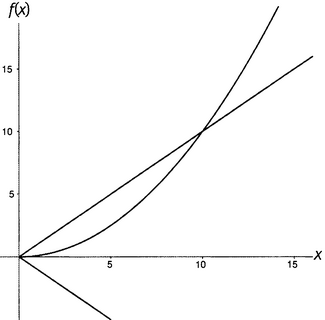
Рисунок 15.2. Функция 0,1x2 не есть Ο(х).
Теперь мы можем оценить значение результата фон Коха 1901 года. Если Гипотеза Римана верна, то при x, стремящемся к бесконечности, абсолютная разность между π(x) и Li(x) — т.е. или Li(x) − π(x), или π(x) − Li(x), что не важно, потому что Ο большому нет дела до знаков, — остается заключенной между двумя ограничивающими кривыми. Ограничивающие кривые — это C√x∙ln x и ее зеркальное отражение, где C — некоторое число. Остаточный член может делать что хочет между этими двумя кривыми, но он никогда не выберется наружу и никогда не вырвется внезапно из-под их контроля. Разность между π(x) и Li(x) есть Ο большое от √x∙ln x.
На рисунке приведен пример функции, которая есть Ο(√x∙ln x). Там показаны: 1) кривая √x∙ln x (верхняя половина отдаленно напоминающей параболу кривой), 2) зеркально отраженная кривая −√x∙ln x (нижняя половина) и 3) придуманная для иллюстрации и ничего особенно не выражающая функция, которая есть Ο(√x∙ln x). Буква m обозначает миллион, ведь вещи подобного рода интересны только для больших аргументов. Стоит отметить, что "функция Дербишира" в действительности на некоторое время вырывается за пределы ограничивающих ее кривых при аргументах, равных примерно 200 миллионам. Это не страшно, поскольку больше она никогда такого не делает. Начиная с некоторой точки — и навсегда после нее — функция остается в пределах границ. Верьте мне, что она там остается, хотя по понятным причинам я и не могу показать вам всю функцию до бесконечности. Ο большое принимает во внимание исключения из правил при малых аргументах (а такие исключения — общее место в теории чисел, взять хотя бы утверждение «все простые числа нечетные… кроме самого первого»).
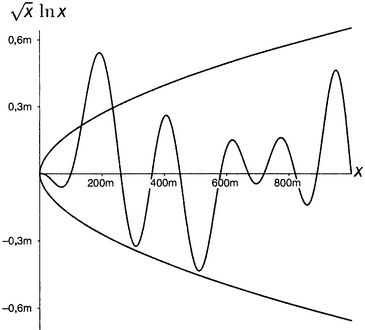
Рисунок 15.3. Функция Дербишира есть Ο(√x∙ln x).
Можно заметить еще, что, поскольку Ο большое не принимает во внимание множители, масштаб по вертикали совершенно произволен. Важны лишь конфигурация — форма ограничивающих кривых — и тот факт, что начиная с какого-то места наша функция навсегда заключена между ними.
III.
Результат фон Коха 1901 года — а именно утверждение, что, если Гипотеза Римана верна, то π(x) = Li(x) + Ο(√x∙ln x), — один из первых примеров определенного типа результатов, которыми сейчас полна теория чисел, — результатов, которые начинаются словами «Если Гипотеза Римана верна, то…». Если окажется, что Гипотеза Римана не верна, то немалую часть теории чисел придется переписывать.
А есть ли какой-нибудь результат типа Ο большого для остаточного члена Li(x) − π(x), который не зависел бы от справедливости Гипотезы Римана? О да. Среди специалистов по аналитической теории чисел долгие годы любимым спортом был поиск все лучших и лучших формул типа Ο большого для остаточного члена. Но ни один не может сравниться с Ο(√x∙ln x). Это абсолютно лучшее, наиболее точное ограничение на остаточный член, известное к настоящему моменту. Правда, раз оно зависит от справедливости Гипотезы, мы не можем быть полностью уверены, что оно верно. Все те оценки остаточного члена, в справедливости которых мы уверены, менее точны, чем эта. Соответствующая параболическая кривая на рисунке несколько шире, причем различие делается все более заметным по мере того, как x уходит на бесконечность. Если же Гипотеза Римана верна, то среди всех известных оценок остаточного члена выражение Ο(√x∙ln x) является наилучшим возможным — наиболее точной формулой типа Ο большого. Оно же и простейшее. При этом все формулы, которые были доказаны без предположения о справедливости Гипотезы, выглядят достаточно уродливо. Вот наилучшая из тех, что известны мне на данный момент:
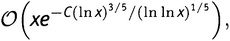
где С — некоторое постоянное число. Ни одна из других подобных формул на вид не проще этой.
Сравним результат фон Коха 1901 года с выделенными курсивом словами в восьмой проблеме Гильберта, приведенной в главе 12.ii. Гильберт перекликался с Риманом, написавшим в своей работе 1859 года, что приближение функции π(x) функцией Li(x) «верно только по порядку величины x1/2». Ну а √x есть, конечно, попросту x1/2. Более того, в главе 5.iv мы видели, что ln x растет медленнее, чем любая положительная степень x, даже самая ничтожно малая. Это можно выразить в терминах Ο большого таким образом: для любого сколь угодно малого числа ε выполнено ln x = Ο(xε). А следовательно (это, правда, не сразу очевидно, но в действительности несложно доказать), можно подставить xε вместо ln x в выражение Ο(√x∙ln x); а поскольку √x — это просто x1/2, можно сложить степени и получить Ο(x1/2+ε). Таким путем получается довольно распространенный вид результата фон Коха: π(x) = Li(x) + Ο(x1/2+ε). Символ ε настолько часто используется для исчезающе малых чисел, что слова «… для любого сколь угодно малого ε» здесь подразумеваются.
Заметим, однако, что, делая эту подстановку, мы слегка ослабили результат фон Коха. Из того, что «остаточный член есть Ο(√x∙ln x)», следует, что «остаточный член есть Ο(x1/2+ε)», но обратное неверно. Эти два утверждения не являются точно эквивалентными. Такое происходит, потому что, как мы видели в главе 5.iv, не только ln x растет медленнее, чем любая степень x, но (ln x)N обладает тем же свойством при любом положительном N. Так что если бы результат фон Коха утверждал, что остаточный член есть Ο(√x∙(ln x)100), то мы все равно в качестве альтернативного вида вывели бы Ο(x1/2+ε)!
Однако запись результата фон Коха в этом слегка ослабленном виде Ο(x1/2+ε) хороша тем, что наводит на размышления. Риман был почти прав в том же смысле, в каком логарифмическая функция есть почти x0; порядок величины есть не х1/2, а x1/2+ε. Если учесть, какие средства имелись у него в наличии, каким было общее состояние знания в данной области и какие численные данные были доступны в то время, то риманово x1/2 все равно должно считаться прозрением потрясающей глубины.
Вводя Ο большое, я начал с истории, так что сейчас, прощаясь с ним, расскажу еще одну. Суть ее в том, что математики, как и другие специалисты, иногда любят напустить туману, чтобы отпугнуть и смутить профанов.
На конференции в Курантовском институте летом 2002 года (см. главу 22) я разговаривал по поводу своей книги с Питером Сарнаком. Питер — профессор математики в Принстонском университете и специалист по теории чисел. Я упомянул, что пытаюсь придумать, как объяснить Ο большое тем читателям, кто с ним незнаком. «О, — сказал Питер, — вам надо бы поговорить с моим коллегой Ником (т.е. Николасом Кацем — он тоже профессор в Принстоне, но занимается в основном алгебраической геометрией). Ник ненавидит Ο большое. Никогда его не использует». Я это проглотил, но взял на заметку, рассчитывая, что смогу придумать, как это использовать в книге. В тот же вечер мне случилось разговаривать с Эндрю Уайлсом, который очень хорошо знает и Сарнака, и Каца. Я упомянул нелюбовь Каца к Ο большому. «Чепуха, — сказал Уайлс, — они просто над вами потешаются. Да Ник все время его использует». И будьте уверены, Кац использовал его в лекции на следующий же день. Своеобразное чувство юмора у математиков.
IV.
Оставим Ο большое. Теперь перед нами функция Мебиуса. Есть несколько способов ввести функцию Мебиуса. Подойдем к ней со стороны Золотого Ключа.
Возьмем Золотой Ключ и перевернем его вверх ногами, т.е. возьмем обратную величину к каждой стороне равенства в выражении . Очевидно, если A = B и при этом ни A, ни B не равны нулю, то 1/A = 1/B. Получаем (15.1)
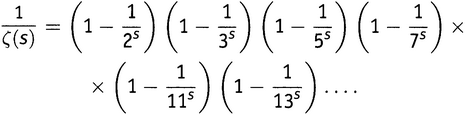
Теперь раскроем скобки в правой части. На первый взгляд, это сильно сказано: как-никак, сомножителей в скобках бесконечно много. На самом деле процедура требует несколько большего внимания и обоснования, чем мы можем здесь ей уделить, но в конце концов мы получим полезный и верный результат, так что в данном случае цель оправдывает средства.
Раскрытие скобок все мы изучали в курсе элементарной алгебры. Чтобы перемножить (а + b)(p + q), сначала умножаем a на (p + q), что дает ар + aq. Затем умножаем b на (p + q), что дает bp + bq. А потом, поскольку в скобках у нас a плюс b, мы складываем вместе то, что получилось, и окончательный ответ имеет вид ap + aq + bp + bq. Если надо перемножить три скобки (а + b)(p + q)(u + v), то повторение этих действий дает apu +aqu + bpu + bqu + apv + aqv + bpv + bqv. Перемножение четырех скобок (а + b)(p + q)(u + v)(x + у) дает
apux + aqux + bpux + bqux + apvx + aqvx + bpvx + bqvx + apuy + aquy + bpuy + bquy + apvy + aqvy + bpvy + bqvy. (15.2)
Грандиозность того, что получается, начинает внушать некоторые опасения. А ведь нам предстоит перемножить бесконечное число скобок! Фокус состоит в том, чтобы посмотреть на это дело глазами математика. Из чего составлено выражение ? Ну, это сумма некоторого числа членов. Как эти члены выглядят? Выберем наугад какой-нибудь один из них, скажем aqvy. Сюда входит a из первой скобки, q из второй, v из третьей и y из четвертой. Это произведение, составленное из чисел, выбранных по одному из каждой скобки. И все выражение целиком получается в результате всех возможных комбинаций того, как мы выбираем эти числа из скобок.
Как только вы смогли это увидеть, перемножение бесконечного числа скобок больше не проблема. В ответе будет сумма — разумеется, бесконечная — членов, каждый из которых получен путем выбора одного числа из каждой скобки и перемножения всего, что выбрали. Если сложить результаты всех таких возможных выборов, то и получится ответ. Однако в том виде, как эта процедура описана, она все еще выглядит несколько устрашающей. Согласно сказанному, каждый член в нашей бесконечной сумме есть бесконечное произведение. Да, так оно и есть, но, поскольку каждая скобка в правой части выражения содержит 1, наша жизнь делается приятнее за счет того, что мы будем выбирать бесконечное число единиц и лишь конечное число не-единиц. В конце концов, поскольку каждый не-единичный член в каждой скобке есть число между −1/2 и 0, перемножение бесконечно большого числа таких членов дает результат, величина которого (я имею в виду — без учета знака) заведомо не больше, чем (1/2)∞, а это равно нулю! Теперь смотрите, как я построю бесконечную сумму.
Первый член в бесконечной сумме: берем 1 из каждой скобки. Это даст бесконечное произведение 1×1×1×1×1×…, значение которого есть, конечно, просто 1.
Второй член: берем 1 из всех скобок, кроме первой. Из первой же возьмем 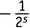 . Это даст бесконечное произведение
. Это даст бесконечное произведение 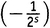 ×1×1×1×1×…, которое равно просто
×1×1×1×1×…, которое равно просто 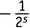 .
.
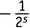 . Это даст бесконечное произведение
. Это даст бесконечное произведение 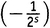 ×1×1×1×1×…, которое равно просто
×1×1×1×1×…, которое равно просто 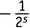 .
.Третий член: берем 1 из каждой скобки, кроме второй. А из второй возьмем 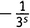 . Это даст бесконечное произведение 1×
. Это даст бесконечное произведение 1×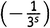 ×1×1×1×…, что равно просто
×1×1×1×…, что равно просто 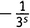 .
.
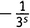 . Это даст бесконечное произведение 1×
. Это даст бесконечное произведение 1×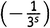 ×1×1×1×…, что равно просто
×1×1×1×…, что равно просто 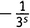 .
.Четвертый член… Я думаю, понятно, что, если брать 1 из каждой скобки, кроме n-й, мы получим слагаемое равное 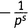 , где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):
, где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):
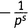 , где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):
, где p — n-е простое число. Итак, получилась бесконечная сумма вида (15.3):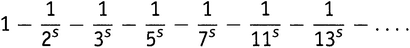
Но это еще не конец. При перемножении скобок возникает сумма всех возможных членов, получаемых взятием одного числа из каждой скобки. Предположим, мы выбрали 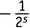 из первой скобки,
из первой скобки, 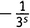 из второй и 1 из всех остальных. Это дает
из второй и 1 из всех остальных. Это дает 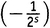 ×
×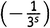 ×1×1×1×…, что равно
×1×1×1×…, что равно 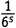 . Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки
. Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки 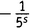 и
и 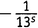 из шестой, а единицы из всех остальных, получаем член, равный
из шестой, а единицы из всех остальных, получаем член, равный 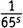 .
.
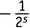 из первой скобки,
из первой скобки, 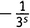 из второй и 1 из всех остальных. Это дает
из второй и 1 из всех остальных. Это дает 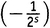 ×
×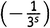 ×1×1×1×…, что равно
×1×1×1×…, что равно 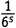 . Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки
. Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобки 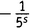 и
и 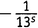 из шестой, а единицы из всех остальных, получаем член, равный
из шестой, а единицы из всех остальных, получаем член, равный 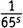 .
.(Заметим, что здесь работают два простых правила арифметики. Одно — это правило знаков, гласящее, что минус умножить на минус дает плюс, а другое — 7-е правило действий со степенями, согласно которому (x×y)n = xn×yn.)
Так что наряду с членами, уже собранными в выражении , имеется новый набор, каждый член в котором происходит из каждой пары простых чисел, как 5 и 13, и которые все входят со знаком плюс. Таким образом, выражение разрослось до такого:
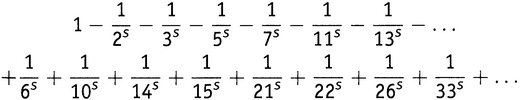
где каждое число во второй строке есть произведение двух различных простых.
А ведь мы едва начали нашу деятельность по перемножению бесконечного числа скобок. Следующий шаг состоит в том, чтобы перебрать все возможные способы выбрать три не-единицы (при всех остальных единицах). Например, 1×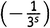 ×1×1×
×1×1×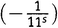 ×
×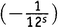 ×1×1×…, из чего возникает
×1×1×…, из чего возникает 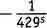 .Теперь результат разрастается до
.Теперь результат разрастается до
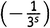 ×1×1×
×1×1×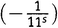 ×
×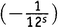 ×1×1×…, из чего возникает
×1×1×…, из чего возникает 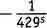 .Теперь результат разрастается до
.Теперь результат разрастается до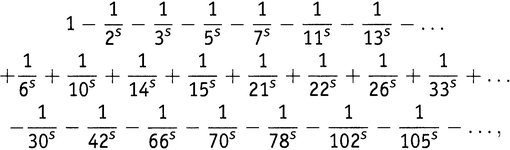
где каждое число в третьей строке есть произведение трех различных простых.
В предположении, что мы продолжаем так поступать, а также в предположении, что получающиеся члены можно переставлять, как мы пожелаем, выражение превращается в следующее (15.4):

Натуральные числа в правой части — это… что? Это заведомо не все натуральные числа: 4, 8, 9 и 12 там отсутствуют. Но и не простые: присутствующие там 6, 10, 14 и 15 не являются простыми. Если оглянуться на процесс перемножения этого бесконечного количества скобок, то станет ясно, что ответ такой: каждое натуральное число, которое равно произведению нечетного числа (включая 1) различных простых, взятое со знаком минус, и, кроме того, каждое натуральное число, которое равно произведению четного числа различных простых, взятое со знаком плюс. Отсутствуют такие числа, как 4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, … — т.е. числа, которые делятся на квадрат некоторого простого.
Поприветствуем функцию Мебиуса! Она названа по имени немецкого математика и астронома Августа Фердинанда Мебиуса (1790–1868).

Рисунок 15.4. Лента Мебиуса и муравей на ней.
В наше время ее общепринято обозначать греческой буквой μ, что произносится как «мю» — греческий эквивалент буквы «м». Приведем полное определение функции Мебиуса.
• Ее область определения есть N, то есть все натуральные числа 1, 2, 3, 4, 5, ….
• μ(1) = 1.
• μ(n) = 0, если среди делителей числа n есть квадрат.
• μ(n) = −1, если число n простое или является произведением нечетного числа различных простых чисел.
• μ(n) = 1, если число n является произведением четного числа различных простых чисел.
Такое определение функции может показаться вам страшно громоздким. Однако функция Мебиуса приносит колоссальную пользу в теории чисел и далее в этой книге будет играть ведущую роль. В качестве примера приносимой ею пользы заметим, что все трудоемкие алгебраические действия, через которые нам пришлось продираться, сводятся к изящному выражению (15.5):
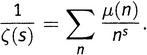
V.
B истории Гипотезы Римана наряду с самой функцией μ(n) не меньшую роль играет ее нарастающее значение, т.е. результат сложения μ(1) + μ(2) + μ(3) + … + μ(k) для некоторого числа k. Так определяется «функция Мертенса» М(k). Ее первые 10 значений (т.е. значения при k = 1, 2, 3, …, 10) равны 1, 0, −1, −1, −2, −1, −2, −2, −2, −1. Функция M(k) весьма нерегулярна — она совершает колебания в обе стороны вокруг нулевого значения в стиле, который математики называют «случайными блужданиями». Для аргументов, равных 1000, 2000, …, 10 000, ее значения равны 2, 5, −6, −9, 2, 0, −25, −1, 1, −23. Для аргументов миллион, 2 миллиона, …, 10 миллионов ее значения равны 212, −247, 107, 192, −709, 257, −184, −189, −340, 1037. Если не обращать внимания на знаки, то видно, что величина функции M(k) возрастает, но помимо этого никакой ясной картины не просматривается.
Из выражения видно, что поведение функций μ и M (накапливающейся μ) жестко привязано к дзета-функции, а тем самым и к Гипотезе Римана. На самом деле если вам удастся доказать приведенную ниже теорему 15.1, то вы сможете заключить, что Гипотеза Римана верна!
Теорема 15.1
M(k) = Ο(k1/2).
Однако если теорема 15.1 не верна, то отсюда еще не следует, что не верна Гипотеза. Математики говорят, что теорема 15.1 сильнее Гипотезы. Слегка ослабленный вариант, сформулированный как теорема 15.2, в точности равносилен Гипотезе:
Теорема 15.2
M(k) = Ο(k1/2+ε) для любого сколь угодно малого числа ε.
Если теорема 15.2 верна, то верна и Гипотеза; а если она не верна, то не верна и Гипотеза. Это в точности эквивалентные теоремы. Мы еще вернемся к этому в главе 20.vi.

