Вся эта несусветица с инвариантами, симметрией и законами сохранения на первый взгляд оторвана от жизни. Перейдем к конкретике.

Представьте себе относительно простую систему – например, рогатку, при помощи которой вы запускаете злых птичек в воздух, чтобы сшибать простенькие заслонки, где прячутся зеленые свинки. В любой момент вы можете определить силу, с которой рогатка действует на птичку, сопротивление воздуха, силу гравитации и тому подобные взаимодействия со всеми твердыми телами в окружающей среде. После чего можно вычислить скорость птички. Повторяйте эти вычисления – и дело в шляпе, вы можете предсказать движение птички!

Так работает физика в игре «Angry Birds», и если это вполне устраивает птичек, а также Ньютона и Галилея, значит, и нас устраивает.

Однако ньютонов подход к физике иногда оказывает нам медвежью услугу. Прежде всего, из него не сразу понятно, почему, собственно, определенные системы ведут себя так, а не иначе.

Позвольте задать простой вопрос: почему свет распространяется по прямой? Ньютон знал, что на это ответить. В нормальной обстановке свет распространяется по прямой, потому что на него не действуют никакие силы. Это и есть краеугольный камень Первого закона Ньютона.

В I в. до н. э. Герон Александрийский, математик и инженер, предложил иную точку зрения на движение света. Свет знает, куда хочет попасть. И выбирает кратчайший путь. Герон играл в эту игру с зеркалами и показал, что если отразить луч при помощи зеркала и направить его в определенную точку, то какую точку ни выберешь, кратчайшим путем окажется тот самый, по какому протянется луч света.

Так вышло, что решение Герона независимо формулирует закон отражения: угол падения равен углу отражения. Хотите проверить закон сами – возьмите вместо фотона теннисный мячик и бросайте его в стенку под каким-нибудь углом.

Шестнадцать веков спустя Пьер де Ферма обобщил этот закон на движение света при любых обстоятельствах.

На первый взгляд это упрощенческое заявление, но на самом деле оно очень лукавое. Откуда свет, собственно, знает, как выбрать самый быстрый маршрут? Если хотите пример из реальной жизни, подойдите к бассейну с мелкого конца и суньте в воду ногу под углом. Обратите внимание, что нога словно бы сломается под поверхностью.

Голландский физик Христиан Гюйгенс дал этому феномену абсолютно ньютонианское объяснение. В воздухе свет распространяется быстрее, чем в воде. Если вы сядете и подумаете об этом, то, вероятно, даже удивитесь. Разве свет не всегда распространяется со скоростью с? На самом деле скорость света – это скорость света в вакууме. А когда начинаешь распространять волны в воде, все замедляется. Грубо говоря, чем плотнее среда, тем медленнее распространяется свет.

Гюйгенс считал, что свет – это последовательность распространяющихся волн. Так и есть. Принцип Гюйгенса гласит, что на каждом шаге распространения свет можно представлять себе как череду расходящихся круглых волн. По ту сторону от поверхности, где вода, волны распространяются медленнее и в результате интерферируют в точности так, что нам кажется, будто свет сгибается вниз.

Представить себе свет как волну почему-то труднее, чем, скажем, звук. Звуковые волны преспокойно забираются за углы, а вот видеть, что за углом, невозможно.

Чем мучиться и воображать картину интерференции бесчисленных круглых волн, распространяющихся на стыке двух сред, давайте лучше представим это себе на наглядной аналогии – куда проще и куда сентиментальнее.

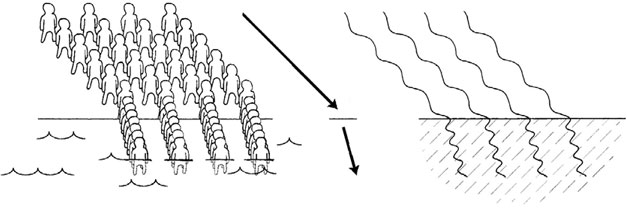
Представьте себе эскадрон солдат, которые идеальным строем шагают по пляжу к океану. Передний ряд расположен под углом к кромке воды, поэтому один из солдат вступит в воду первым, за ним второй, третий – и в конце концов в воду войдет последний в ряду. Естественно, такое же повторится и со всеми остальными рядами. Идти по воде получается гораздо медленнее, чем по пляжу, поэтому те солдаты, которые ступят в воду первыми, заметно затормозятся. Те, кто войдет в воду сразу после этого, едва не налетят на них. В процессе угол, под которым ряды расположены к кромке воды, станет гораздо острее.

Принцип Ферма дает нам другой подход, который не требует рассуждений о том, что происходит в каждый отдельно взятый миг как с лучом света, так и с солдатами, представьте себе, что на берегу сидит мускулистый красавец – прямо как Дэвид Хассельхофф в «Спасателях Малибу». Он видит пловца, который борется с волнами. Какой маршрут ему выбрать? Опять же по берегу он может бежать гораздо быстрее, чем в воде. Значит, ему нужно покрыть как можно больше горизонтального расстояния по берегу, а потом поплыть перпендикулярно кромке воды, чтобы добраться до утопающего как можно скорее.

Но вот что поразительно: стоит пробиться через математические выкладки, и выяснится, что у Гюйгенса и у Ферма получаются одинаковые пути. Вычисления Гюйгенса ничего не говорят о глобальных свойствах системы. Каждый солдат изо всех сил старается шагать по прямой, но сопротивление воды искривляет картину переднего ряда.

Эмпирические отношения, описывающие преломление света на стыке двух сред, известны уже довольно давно. Это называется закон Снеллиуса, и открыл его в 1621 году голландский математик с потрясающим именем Виллеброрд Снеллиус.

Закон Снеллиуса – это простое соотношение между углом, под которым свет попадает на поверхность, где ему предстоит преломиться, относительной скоростью света в разных средах и углом, под которым свет выйдет с другой стороны. С практической точки зрения, если вы хотите делать линзы или любую другую оптику, больше вам ничего знать и не требуется. Вся эта интерференция волн и минимизация пути света даже и не нужны!

Чем же так полезен подход Ферма при всей своей извилистости? В лучшем случае просто получишь тот же результат, что и при применении принципа Гюйгенса. Дело в том, что принцип Ферма придуман не для того, чтобы получить правильный ответ: он призван объяснить, что происходит на самом деле.

Принцип Ферма оказался на удивление полезен для современных открытий. Один из поразительных прогнозов, которые дала общая теория относительности, – время возле массивного тела, например, звезды или черной дыры, течет медленнее, чем вдали от него. Поскольку свет по-прежнему хочет пробежать по самому быстрому маршруту, он отклонится от прямой линии, чтобы объехать вызванные гравитацией пробки поблизости от черной дыры. Проще говоря, тот самый принцип, который предсказывает поведение призм, предсказывает и то, что массивные тела искривляют свет.

Часто бывает, что самый короткий путь – не прямой. Вот, например, вам нужно добраться из Филадельфии в Пекин. Какой маршрут выбрать? Если вам случалось летать трансокеанским рейсом и, чтобы не свихнуться от скуки, наблюдать за перемещением самолета по компьютерной карте, возможно, вы заметили, что самолет летит не по той линии, которая вам по наивности представлялась прямой. Пекин с Филадельфией находятся примерно на одной широте – около 40 градусов. И все же путь, по которому полетит ваш самолет, пройдет севернее Аляски.

Этот путь по большой дуге проделывает именно то, что предлагает Ферма. Это тот маршрут между Филадельфией и Пекином, который минимизирует дистанцию. Примерно то же самое у вас получится, если вы возьмете глобус, воткнете булавки в точки старта и финиша и туго-туго натянете между ними резинку. На карте большая дуга выглядит странно, однако это самый естественный маршрут в мире. Если вы полетите по прямой и нанесете свой маршрут на карту, как в кино про Индиану Джонса, путь по большой дуге получится сам собой.

Однако Ферма, как вы вскоре убедитесь, не просто подсказывает ближайший путь до Пекина – он еще и закладывает фундамент для формулирования всех физических законов, основанных на симметрии, а это возвращает нас прямиком к Эмми Нётер.