Принцип Ферма очень хорош и правилен, если нас интересует исключительно распространение света, но если мы пытаемся разобраться в устройстве мироздания, придется копнуть поглубже. Принцип Ферма не объясняет создание частиц и античастиц, существование сил, полей, расширение вселенной и примерно миллион прочих явлений, наблюдаемых во вселенной, где мы живем.

У физиков и математиков – а в XVII веке разница между ними совсем не была колоссальной – подобные задачи на минимизацию нашли выражение в попытках найти новые интересные способы приложения только что открытых законов Ньютона. Одна из самых известных задач того времени – поиск кривой под названием «брахистохрона».

Представьте себе, что вы хотите построить самые-самые распрекрасные американские горки – ну чтобы уж точно все ахнули. Вы можете предельно минимизировать силу трения, но при попытках построить идеальную форму непременно наткнетесь на маленькую математическую тайну. Проектировать американские горки надо так, чтобы вагонетка, стартующая из состояния покоя в точке А, как можно быстрее очутилась внизу, в точке В.

Загадка брахистохроны не теряла актуальности некоторое время, а потом, в 1696 году, Иоганн Бернулли – представитель очень знаменитой семьи, где было много выдающихся математиков – заявил, что решил задачу, и не без самодовольства поставил ее перед другими математиками: потягайтесь, мол, со мной.

Сам Бернулли придумал очень хитроумное решение задачи, так что похвалялся он, наверное, не зря. Вагонетка американских горок едет чем ближе к земле, тем быстрее – а Бернулли представил себе очень сложную линзу, материал которой чем выше, тем плотнее, так что свет, проходя сквозь нее сверху вниз, будет бежать чем ближе к земле, тем быстрее. Потом Бернулли применил принцип Ферма – и потребовал, чтобы луч прошел заданное расстояние за минимальное время.

Полученная кривая получила название перевернутой циклоиды и очень похожа на обычную миску, только очень точную, математически выведенную.

Все это стало возможным в основном благодаря тому, что лет за десять до этого Исаак Ньютон опубликовал свой трактат «Principia Mathematica». К тому времени, как Бернулли опубликовал свой вызов, Ньютон уже работал управляющим Королевского монетного двора, однако же нашел время подумать над задачей о брахистохроне. Решил он ее за один вечер перед сном – совсем иначе, чем Бернулли, геометрическим методом. Был он таким математическим врединой, что даже не стал подписываться. Но Бернулли все равно понял, кто это, отметив: «По когтю опознаю льва».

Находить форму кривых в XVII веке было очень модно. Другая знаменитая задача касалась поиска кривой с названием «таутохрона». Если сделать американские горки такой формы, то откуда бы вы ни пустили вагонетку, она доберется до низу за одно и то же время. Эту задачу решил в 1659 году Христиан Гюйгенс – тот самый, что описал свет как волну. Почему это такое большое достижение, становится понятно, если учесть, что до публикации «Principia Mathematica» оставалось еще почти 30 лет.

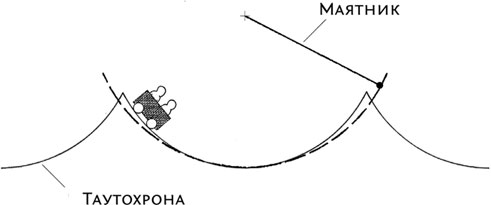
Я заговорил о таутохроне, поскольку выясняется, что она представляет собой точно такую же кривую, что и брахистохрона – циклоиду. Помимо того, что таутохрона – ответ на математическую задачу, она приносит много пользы, поскольку на тех же принципах можно построить и точные часы. На протяжении почти всей мировой истории единственными точными часами на свете было Солнце, а поскольку XVII век был периодом географических открытий и мореплавания, солнечные часы, конечно, уже не годились.

Обратите внимание, что в самом низу таутохрона очень похожа на кривую, которую описывает маятник. И не случайно. Маятники потому и позволяют часам так точно отмерять время, что при условии, что отклонение будет относительно малым, колебания занимают в точности одно и то же время – вот почему дуга маятника так хорошо вписывается в донышко циклоиды. Галилей еще в юности отметил этот факт экспериментально. Ему было скучно, он наблюдал за колебаниями люстры в соборе в Пизе и отметил, что размах колебаний уменьшается, однако время (в ударах сердца) остается постоянным.

Итак, перед нами интересный вопрос: судя по всему, движение частиц, волн и света определяется решениями одних и тех же задач на минимизацию. Найди путь, по которому луч света попадет из точки А в точку В за минимальное время – и надо же, найдешь ту линию, которую он опишет в реальной жизни!

Задачи о брахистохроне и таутохроне показывают, что точно так же можно рассуждать и о движении частиц, обладающих массой. Похоже, минимизация времени в пути – это нечто глубинное и важное.

Ньютон и Бернулли потому-то (отчасти) и были гениями, что сумели решить эти задачи, не располагая никаким общим руководством к решению. В сущности, им пришлось угадывать и перебирать возможные решения, пока они не пришли к идее самого короткого времени.

Все изменилось в XVIII веке, когда Леонард Эйлер и его ученик Жозеф Луи Лагранж обнаружили общее правило, которое позволило им минимизировать по траектории любую величину – хоть время, хоть расстояние.

Не хотелось бы погрязнуть в математике, поэтому давайте вспомним знакомый пример: полет из Филадельфии в Пекин. Возможных путей из одной точки в другую буквально бесконечное множество, хотя большинство из них предполагает извивы и зигзаги. А мы хотим найти простое соотношение, связывающее путь, который нам нужен – то есть тот, который окажется короче всего – с реальностью, в которой нам надо двигаться по выгнутой поверхности Земли.

Эйлер и Лагранж описали способ вычислить кратчайший путь, и неудивительно, что их метод в значительной степени опирался на недавно разработанные Ньютоном методы математического анализа.