Всего через год после выхода книги Льюиса и независимо от него Дональд Рубин начал работать над серией статей, в которой представлены потенциальные результаты как язык для постановки вопросов о причинности. Рубин, в то время статистик службы тестирования в образовании, в одиночку нарушил молчание о причинно-следственных связях, которое сохранялось в статистике на протяжении 75 лет, и легитимировал концепцию контрфактивности в глазах многих ученых-медиков. Важность этого достижения нельзя переоценить. Исследователи получили гибкий язык для выражения почти любых каузальных вопросов, которые они могли бы задать и о группе людей, и об отдельных индивидах.

В каузальной модели Рубина потенциальный результат для переменной Y — это просто «значение, которое Y принял бы для отдельного u, если бы X было присвоено значение x». Здесь очень много слов, поэтому часто удобнее записать эту величину более компактно: Y_X = _X (u). Нередко мы сокращаем это до Y_X (u), если из контекста очевидно, какой переменной присваивается значение X.

Чтобы оценить смелость такого рода записи, стоит отвлечься от символов и подумать о том, что за ними стоит. Записывая символ Y_X, Рубин утверждал, что Y определенно приобрел бы какое-то значение, если бы X был равен x, и этот факт объективно реален в той же степени, что и значение, которое Y получил на самом деле. Если вы не согласны с этим допущением (а я уверен, что Гейзенберг с ним не согласился бы), то не сможете использовать потенциальные результаты. Также обратите внимание, что потенциальный, или контрфактивный, результат определяется на уровне отдельного человека, а не группы.

Впервые потенциальные результаты появились в магистерской диссертации Ежи Неймана, написанной в 1923 году. Нейман, потомок польских аристократов, вырос в изгнании в России, где получил очень сильное математическое образование, и оказался на родине только в 1921 году, когда ему было 27 лет. Он хотел продолжить исследования в области чистой математики, но ему было легче найти работу статистика. Как и Р. Э. Фишер в Англии, он провел первое статистическое исследование в сельскохозяйственном институте и оказался слишком высококвалифицированным для этой работы. Он был не только единственным статистиком в институте, но и единственным человеком в стране, который думал о статистике как о научной дисциплине.

Первое упоминание о потенциальных результатах Нейман сделал в контексте сельскохозяйственного эксперимента, где нижний индекс представляет «неизвестный потенциальный урожай i-й разновидности [данного семени] на соответствующем участке». Тезис оставался неизвестным и не переводился на английский до 1990 года. Однако сам Нейман неизвестным не остался. Он договорился провести год в статистической лаборатории Карла Пирсона в Университетском колледже Лондона, где подружился с сыном Пирсона Эгоном. Эти двое поддерживали связь в течение следующих семи лет, и их сотрудничество принесло большие плоды: подход Неймана — Пирсона к статистической проверке гипотез стал важной вехой, о которой узнает каждый начинающий студент-статистик.

В 1933 году длительное автократическое правление Карла Пирсона наконец подошло к концу с его уходом на пенсию, и Эгон стал его естественным преемником или оказался бы таковым, если бы не единственная проблема в виде Р. Э. Фишера, к тому времени самого известного статистика в Англии. Университет предложил уникальное и катастрофическое решение, разделив территорию Пирсона на кафедру статистики (Эгон Пирсон) и кафедру евгеники (Фишер). Эгон, не теряя времени, нанял своего польского друга. Нейман прибыл в 1934 году и почти сразу же схлестнулся с Фишером.

Фишер уже рвался в бой. Он знал, что является ведущим статистиком мира и во многом практически изобрел этот предмет, однако ему было запрещено преподавать на отделении статистики. Отношения были необычайно напряженными. «Комнату преподавателей тщательно делили, — пишет Констанс Рид в своей биографии Неймана. — Группа Пирсона пила чай в 4 часа; в 4:30, когда они благополучно удалялись, десантировалась группа Фишера».

В 1935 году Нейман прочитал в Королевском статистическом обществе лекцию под названием «Статистические проблемы сельскохозяйственных экспериментов», в которой подверг сомнению некоторые методы Фишера, а также между прочим обсудил идею потенциальных результатов. Когда Нейман закончил, Фишер встал и заявил, что «надеялся, что статья доктора Неймана будет посвящена теме, с которой автор полностью знаком».

«[Нейман] утверждал, что Фишер был неправ, — писал Оскар Кемпторн много лет спустя об этом инциденте. — Это было непростительное преступление — Фишер никогда не ошибался, и предположение о том, что это, возможно, расценивалось как вооруженное нападение. Всякий, кто не принимал писания Фишера как данную Богом истину, был в лучшем случае глупцом, а в худшем — злодеем». Несколько дней спустя Нейман и Пирсон увидели всю силу его гнева, когда вечером пришли на факультет и обнаружили разбросанные по полу деревянные модели Неймана, которыми он иллюстрировал свою лекцию. Они пришли к выводу, что только Фишер мог устроить эти разрушения.

Хотя сейчас этот приступ ярости покажется забавным, позиция Фишера имела серьезные последствия. Конечно, он не был способен обуздать свою гордость и использовать запись потенциального результата, предложенную Нейманом, хотя это помогло бы ему позже с проблемами медиации. Отсутствие языка потенциальных результатов привело его и многих других к так называемой ошибке посредничества, которую мы обсудим в главе 9.

На этом этапе некоторые читатели, вероятно, все еще считают концепцию контрфактивности несколько мистической, поэтому я хотел бы показать, как некоторые последователи Рубина делают выводы о потенциальных результатах, и противопоставить этот безмодельный подход структурной причинно-следственной модели.

Представим, что мы изучаем конкретную компанию, пытаясь понять, что сильнее влияет на зарплату сотрудника — образование или многолетний стаж. Мы собрали данные о существующих зарплатах в этой компании и записали их в табл. 12. Условимся, что EX — стаж, ED — образование, S — зарплата. Также для простоты предположим, что существуют три уровня: 0 = средняя школа, 1 = высшее образование, 2 = ученая степень. Таким образом, S_ЕD = 0(u) или S₀(u) представляет собой зарплату человека u, если u окончил среднюю школу, но не университет, а S₁(u) представляет зарплату u, если бы тот окончил университет. Типичный контрфактивный вопрос, который можно было бы задать, звучит так: какой была бы зарплата Элис, если бы у нее было высшее образование? Другими словами, чему равна S₁ (Элис)?

Первое, на что следует обратить внимание в табл. 12, — это отсутствующие данные, отмеченные вопросительными знаками. Для одного и того же человека нельзя увидеть более одного потенциального результата. Несмотря на всю очевидность, это важное утверждение. Статистик Пол Холланд однажды назвал его фундаментальной проблемой причинного вывода, и название прижилось. Если бы мы могли заполнить клетки с вопросительными знаками, то ответили бы на все наши вопросы о причинности.

Я никогда не был согласен с представлением Холланда об отсутствующих данных в табл. 12 как о «фундаментальной проблеме», возможно, потому, что я редко представлял проблемы причинности в виде таблицы. Но если подойти к делу фундаментально, становится понятно, что его подход чреват огромными заблуждениями, что мы вскоре увидим. Обратите внимание, что, помимо декоративных заголовков последних трех столбцов, табл. 12 полностью лишена каузальной информации о ED, EX и S, например о том, влияет образование на заработную плату или наоборот. Хуже того, она не позволяет нам представлять такую информацию, даже когда она доступна. Но статистикам, которые видят фундаментальную проблему в отсутствии данных, такая таблица, кажется, открывает безграничные возможности. Действительно, если смотреть на S₀, S₁ и S₂ не как на потенциальные результаты, а как на обычные переменные, у нас есть десятки методов интерполяции для заполнения пробелов или, как сказали бы статистики, условного расчета недостающих данных некоторым оптимальным образом.

Таблица 12. Вымышленные данные для примера с потенциальными результатами

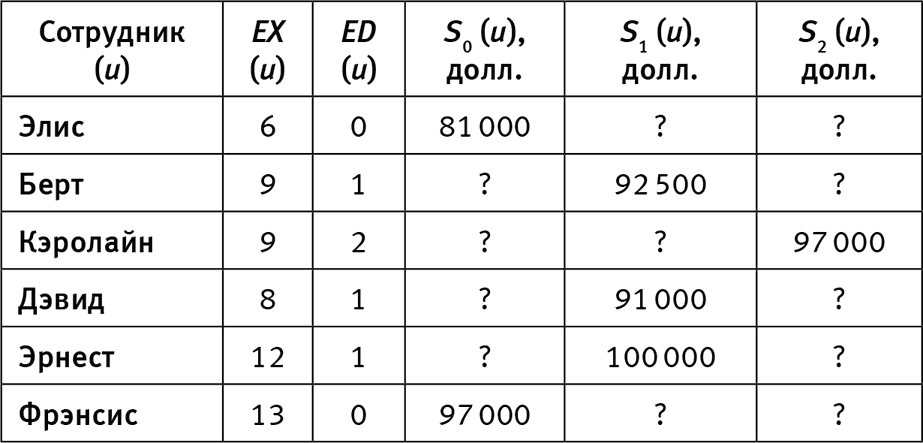
Один из распространенных подходов — сопоставление. Мы ищем пары людей, которые хорошо совпадают по всем переменным, кроме интересующей нас, а затем заполняем их строки, чтобы они соответствовали друг другу. Явный пример здесь — случай Берта и Кэролайн, которые идеально совпадают по стажу. Мы предполагаем, что, если бы у Берта была магистерская степень, он получал бы столько же, сколько Кэролайн (97,0 тысяч долларов), а если бы у Кэролайн была только степень бакалавра, она получал бы, как Берт (92,5 тысяч долларов). Обратите внимание, что сопоставление подразумевает ту же идею, что и ограничение по какому-то фактору (или расслоение): мы выбираем для группы, которые разделяют наблюдаемую характеристику, и используем сравнение, чтобы сделать вывод о характеристиках, которые у них, похоже, не совпадают.

Зарплату Элис трудно оценить таким образом, потому что в данных, которые я привел, для нее нет совпадения. Тем не менее статистики разработали весьма тонкие методы, чтобы сделать условный расчет на основе приблизительных совпадений, и Рубин был одним из пионеров этого подхода. К сожалению, даже самые одаренные его представители не могут превратить данные в потенциальные результаты — даже приблизительно. Ниже я покажу, что правильный ответ принципиально зависит от того, влияет образование на опыт или наоборот, о чем в таблице нет никакой информации.

Второй возможный метод — это линейная регрессия (не путать со структурными уравнениями). В этом подходе мы делаем вид, что данные пришли из какого-то неизвестного случайного источника, и используем стандартные статистические методы, чтобы найти линию (или в данном случае плоскость), которая наилучшим образом соответствует данным. Результатом такого подхода выступает уравнение, которое выглядит следующим образом:

Уравнение (4) говорит нам, что базовая зарплата сотрудника без опыта и только с аттестатом об окончании средней школы составляет (в среднем) 65,0 тысяч долларов. За каждый год опыта заработная плата увеличивается на 2,5 тысяч, а за каждую дополнительную образовательную ступень (до двух) зарплата увеличивается на 5,0 тысяч долларов. Соответственно, аналитик регрессии заявил бы, что наша оценка заработной платы Элис, если бы та имела высшее образование, составляла $65 000 + $2 500 ¥ 6 + $5 000 ¥ 1 = $85 000.

Простота и привычность таких методов объясняет, почему представление Рубина о причинном выводе как о проблеме отсутствия данных пользуется популярностью. Увы, какими бы безобидными ни казались эти методы интерполяции, они в корне ошибочны. Они основаны на данных, а не на модели. Все недостающие сведения заполняются путем изучения других значений в таблице. Как мы узнали благодаря Лестнице Причинности, любой такой метод обречен с самого начала; никакие методы, основанные лишь на данных (первый уровень), не могут ответить на контрфактивные вопросы (третий уровень).

Прежде чем сравнить эти методы со структурной каузальной моделью, давайте исследуем, почему условный расчет без учета модели не работает. В частности, объясним, почему Берт и Кэролайн, которые идеально соответствуют друг другу в плане опыта, на самом деле могут быть совершенно несравнимы, когда дело дойдет до потенциальных результатов. Еще удивительнее, что рациональная причинно-следственная история (подходящая для табл. 12) показала бы: наибольшее соответствие по зарплате у Кэролайн будет с тем, кто не соответствует ей по стажу.

Для начала нужно понять, что стаж, скорее всего, будет зависеть от образования. В конце концов, сотрудникам, получившим диплом, потребовалось для этого четыре года жизни. Таким образом, если бы у Кэролайн была только одна ступень образования (как у Берта), она могла бы использовать это дополнительное время, чтобы получить больший стаж. В этом случае у нее было бы такое же образование, но стаж солиднее, чем у Берта. Таким образом, мы можем заключить, что S₁ (Кэролайн) > S₁ (Берт) вопреки тому, что предсказывало бы наивное сопоставление. Мы видим, что, если у нас есть причинно-следственная история, в которой образование влияет на стаж, сопоставление на основе последнего приведет к несоответствию в потенциальной зарплате.

Удивительно, но равный стаж, который вначале выглядел как приглашение к поиску соответствий, теперь превратился в громкое предупреждение против него. Табл. 12, конечно же, продолжит молчать о таких опасностях. По этой причине я не разделяю стремление Холланда рассматривать причинный вывод как проблему отсутствия данных. Наоборот. Недавняя работа Картики Мохан, моей бывшей студентки, показывает, что даже стандартные задачи с отсутствующими данными нуждаются в причинно-следственном моделировании для их решения.

Теперь давайте посмотрим, как те же данные будут обработаны с помощью структурной причинно-следственной модели. В первую очередь, прежде чем даже посмотрим на данные, нарисуем диаграмму причинности (рис. 53). На ней представим причинно-следственную историю, стоящую за данными, согласно ей стаж «слушает» образование, а зарплата — и то и другое. Фактически мы определили важные вещи, просто взглянув на диаграмму. Если бы наша модель была неправильной и EX было бы причиной ED, а не наоборот, то стаж был бы конфаундером и подбор сотрудников с аналогичным опытом был бы полностью уместным. С ED как причиной EX стаж выступает в роли посредника. Как вы уже наверняка знаете, если перепутать медиатор с конфаундером, мы совершим один из самых страшных грехов в области причинного вывода, что приведет к вопиющим ошибкам. Конфаундер нуждается в поправке, медиатор ее не допускает.

До этого момента в книге я использовал весьма неформальное слово «слушание», чтобы показать, что я имею в виду под стрелками на диаграмме причинности. Но теперь пришло время добавить немного математической плоти к этой концепции. Именно здесь структурные причинно-следственные модели отличаются от байесовских сетей или регрессионных моделей. Когда я говорю, что зарплата слушает образование и стаж, я имею в виду, что такова математическая функция этих переменных: S = f_S (EX, ED). Но нам нужно учитывать индивидуальные вариации, поэтому мы расширяем эту функцию и записываем ее как S = f_S (EX, ED, U_S), где U_S означает ненаблюдаемые переменные, которые влияют на заработную плату. Мы знаем, что эти переменные существуют (например, Элис дружит с президентом компании), но они слишком разнообразны и многочисленны, чтобы явно включить их в нашу модель.

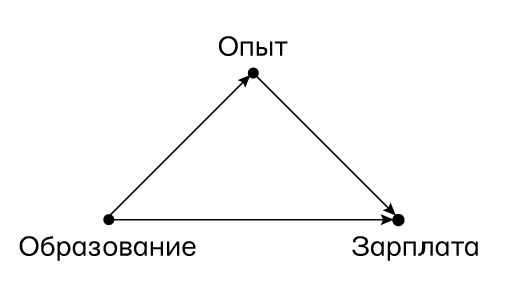
Рис. 53. Диаграмма причинности, показывающая эффект воздействия образования (ED) и стажа (EX) на зарплату (S)

Давайте посмотрим, как это отразится на нашем примере образования / стажа / заработной платы, предполагая во всем линейные функции. Мы используем те же статистические методы, что и раньше, с целью найти наиболее подходящее линейное уравнение. Результат будет выглядеть так же, как уравнение (4), но с одним небольшим отличием:

Однако формальное сходство между уравнениями (4) и (5) глубоко обманчиво; их интерпретации различаются как день и ночь. Тот факт, что мы решили регрессировать S по ED и EX в уравнении (4), никоим образом не означает, что S слушает ED и EX в реальном мире. Это был исключительно наш выбор, и наши данные никак не помешали бы нам регрессировать EX по ED и S или следовать любому другому порядку. (вспомните открытие Фрэнсиса Гальтона, описанное в главе 2, о том, что регрессия не видит причины). Мы теряем эту свободу, когда объявляем уравнение структурным. Другими словами, автор уравнения (5) должен взять на себя обязательство составлять выражения, отражающие его представления о том, кто кого слушает в реальном мире. В нашем случае он считает, что S действительно слушает EX и ED. Что еще более важно, отсутствие уравнения ED = f_ED (EX, S, U_ED) в модели означает, что ED предположительно не учитывает изменения в EX или S. Это различие в обязательствах дает структурным уравнениям возможность поддерживать контрфактивность, что нереально для уравнений регрессии.

В соответствии с рис. 53 у нас также должно быть структурное уравнение для EX, но теперь мы установим коэффициент при S как равный нулю, чтобы отразить отсутствие стрелки от S к EX. После того как мы оценим коэффициенты на основе имеющихся данных, уравнение будет выглядеть примерно так:

Это уравнение говорит о том, что средний стаж для людей без степени магистра составляет десять лет и что каждая ступень образования (до двух) снижает EX в среднем на четыре года. Кроме того, обратите внимание на ключевое различие между структурными уравнениями и уравнениями регрессии: переменная S не входит в уравнение (6), несмотря на то, что S и EX, вероятно, сильно коррелированы. Это отражает уверенность аналитика в том, что на стаж EX, приобретенный любым человеком, никак не влияет его текущая зарплата.

Теперь давайте продемонстрируем, как выводить контрфактивные суждения из структурной модели. Чтобы оценить зарплату Элис, если бы у нее было высшее образование, мы сделаем три шага.

1. Абдукция: используйте данные об Элис и других сотрудниках, чтобы оценить ее специфические факторы: U_S (Элис) и U_EX (Элис).

2. Действие: используйте оператор do, меняя модель так, чтобы она отражала контрфактивное допущение — в данном случае о наличии у нее высшего образования: ED (Элис) = 1.

3. Прогноз: рассчитайте новую зарплату Элис, используя модифицированную модель и обновленную информацию об экзогенных переменных: U_S (Элис), U_EX (Элис) и ED (Элис). Эта рассчитанная заново зарплата равна S_ED = 1 (Элис).

Для шага 1 мы извлекаем из наших данных сведения, что EX (Элис) = 6 и ED (Элис) = 0. Мы подставляем эти значения в уравнения (5) и (6). Затем уравнения сообщают нам специфические для Элис факторы: U_S (Элис) = $1 000 и U_EX (Элис) = –4. Они представляют все уникальное, особенное и чудесное, что есть в Элис. Что бы это ни было, оно добавляет 1 000 долларов к ее прогнозируемой зарплате.

Шаг 2 велит нам использовать do-оператор, чтобы стереть стрелки, указывающие на переменную, для которой установлено контрфактивное значение (образование), и присвоить Элис диплом бакалавра (образование = 1). В этом примере шаг 2 тривиален, потому что нет стрелок, указывающих на образование, и, следовательно, нет стрелок, которые нужно стереть. Однако в более сложных моделях удаление стрелок нельзя пропустить, потому что оно влияет на вычисления в шаге 3. Переменным, которые могли повлиять на результат через промежуточную переменную, больше не разрешается это делать.

Наконец, шаг 3 предполагает обновление модели с целью отразить новую информацию: U_S = $1 000, U_EX = –4 и ED = 1. Сначала мы используем уравнение (6), чтобы пересчитать, каким был бы стаж Элис, если бы она училась в колледже: EX_ED = 1 (Элис) = 10 — 4–4 = 2 года. Затем мы используем уравнение (5), чтобы пересчитать ее потенциальную зарплату:

Наш результат S₁ (Элис) = $76 000 — это действительная оценка потенциальной зарплаты Элис; т. е. совпадение возможно, если допущения модели верны. Поскольку в примере используется очень простая причинно-следственная модель и элементарные (линейные) функции, различия между ней и методом регрессии на основе данных могут показаться незначительными. Но незначительные различия на поверхности отражают огромные различия в глубине. Какой бы контрфактивный (потенциальный) результат мы ни получили от структурного метода, он логически следует из допущений, отраженных в модели. В то же время результат, полученный с помощью метода, основанного на данных, будет так же своеобразен, как и ложные корреляции, поскольку он оставляет эти допущения неучтенными.

Этот пример заставил нас углубиться в тонкости причинно-следственных моделей, сильнее, чем где-либо выше в этой книге. Но позвольте мне сделать небольшое отступление и порадоваться чуду, которое стало возможным благодаря случаю с Элис. Используя комбинацию данных и модели, мы смогли предсказать поведение индивида (Элис) в полностью гипотетических условиях. Конечно, бесплатного сыра не бывает: мы получили такие веские результаты, потому что сделали веские допущения. Мы не только утвердили причинно-следственные связи между наблюдаемыми переменными, но и предположили, что функциональные связи были линейными. Но линейность здесь не так важна, как знание этих конкретных функций. Они позволили нам вычислить специфические особенности Элис по ее наблюдаемым характеристикам и обновить модель, как того требует трехэтапная процедура.

Рискуя несколько омрачить нашу радость, я должен сказать, что эта функциональная информация не всегда будет доступна на практике. В целом мы называем модель полностью заданной, если функции, выраженные стрелками, известны, и частично заданной — в иных случаях. Например, как и в байесовских сетях, мы можем знать только вероятностные отношения между родителями и детьми. Если модель задана частично, мы не оценим точно зарплату Элис; вместо этого нам, скорее всего, придется сделать утверждение с вероятностным интервалом, предположим: «Вероятность того, что ее зарплата составит 76 000 долларов, составляет 10–20 %». Но даже таких вероятностных ответов достаточно для многих случаев. Более того, действительно поражает, сколько информации мы в состоянии извлечь из диаграммы причинности, даже если у нас нет сведений о конкретных функциях, скрытых за стрелками, или есть лишь очень общие данные, скажем предположение о монотонности, с которым мы столкнулись в последней главе.

Шаги с 1 по 3, описанные выше, можно суммировать в первом законе причинного вывода, как я его называю: Y_X (u) = Y_MX (u). Это то же самое правило, которое мы использовали в примере с расстрельной командой в главе 1, только функции здесь другие. Первый закон гласит, что потенциальный результат Y_X (u) можно условно исчислить, перейдя к модели M_X (с удаленными стрелками к X) и вычислив в ней результат Y (u). Отсюда следуют все оцениваемые величины на второй и третьей ступенях Лестницы Причинности. Короче говоря, сведение контрфактивных суждений к алгоритму позволяет нам завоевать столько территории на третьем уровне, сколько позволит математика, но, конечно, ни на йоту не больше.