Дебаты о каузальном воздействии курения происходили по крайней мере за два поколения до того, как каузальные диаграммы могли бы в них поучаствовать. Мы уже рассмотрели, как неравенство Корнфилда помогло уверить исследователей, что ген курильщика, или конституциональная гипотеза, — очень неправдоподобное предположение. Однако более радикальный подход с использованием каузальных диаграмм пролил бы больше света на гипотетический ген и, вероятно, полностью исключил его из дальнейшего обсуждения.

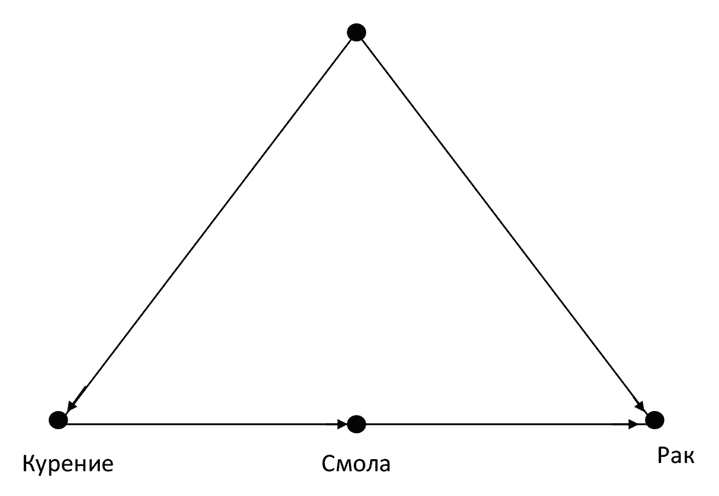
Рис. 41. Гипотетическая каузальная диаграмма для связи курения и рака легких, подходящая для поправок парадного входа

Предположим, что исследователи прошлого смогли измерить отложения смол в легких курильщиков. Еще в 1950-х это называлось в качестве одной из промежуточных стадий в развитии рака легких. Предположим также, что мы, совсем как министр здравоохранения, хотим исключить гипотезу Р. Э. Фишера о том, что ген курильщика является конфаундером по отношению к привычке курить и раку легких. Тогда ситуацию выше описывает каузальная диаграмма на рис. 41.

Рисунок 41 включает два очень важных допущения, которые будут важны для целей нашего примера. Первое: ген курильщика не оказывает никакого воздействия на формирование отложений смол, которые зависят исключительно от физического действия сигаретного дыма (это допущение отражено на схеме отсутствием стрелки между геном курильщика и смолой; оно, однако, не исключает случайные факторы, не имеющие отношения к гену курильщика). Второе значительное допущение состоит в том, что курение ведет к раку только через накопления отложений смол. Таким образом, на схеме нет прямой стрелки от курения к раку и нет также других непрямых путей.

Допустим, что мы выполняем исследование на основе наблюдаемых данных и собрали информацию по курению, смоле и раку для каждого из участников. Нам, к сожалению, недоступны данные по гену курильщика, потому что неизвестно, существует ли такой ген. Поскольку таким образом у нас отсутствуют сведения по переменной-конфаундеру, мы не в состоянии заблокировать путь через черный ход курение ← ген курильщика → рак. Таким образом, мы не можем и использовать поправки черного хода для устранения воздействия конфаундера. Поэтому нам придется искать другие способы. Вместо перемещения черным ходом мы пойдем через парадный вход! В приведенном случае это прямой каузальный путь курение → смола → рак, для которого у нас есть данные по всем трем переменным. Интуитивно мы рассуждаем следующим образом. Прежде всего, мы в состоянии оценить средний каузальный эффект влияния курения на смолу, потому что на схеме нет незаблокированных путей через черный ход от курения к раку — путь курение ← ген курильщика → рак ← смола уже заблокирован схождением у переменной рак. Поскольку этот путь уже заблокирован, нам даже не нужна поправка черного хода. Мы просто наблюдаем вероятности P (смола | привычка курить) и P (смола | отсутствие привычки курить), а разница между ними и будет средним каузальным воздействием курения на смолу. Аналогично диаграмма позволяет нам оценить среднее каузальное воздействие смолы на рак. Чтобы сделать это, мы заблокируем путь черного хода от смолы к раку: смола ← курение ← ген курильщика → рак, введя поправки по курению. Здесь пригодятся уроки главы 4: нам нужны только данные по минимальному достаточному набору переменных, снимающих осложнения (здесь — курение). Тогда формула поправки черного хода даст нам вероятности P (рак | do (смола)) и P (рак | do (отсутствие смолы)). Разница между этими двумя вероятностями и будет средним каузальным воздействием смолы на рак.

Теперь нам известно среднее увеличение вероятности отложения смол благодаря курению и среднее увеличение вероятности заболеть раком из-за отложения смол. Можем ли мы как-либо объединить эти вероятности, чтобы получить средний рост заболеваемости раком из-за курения? Да, можем. Рассуждаем мы при этом таким образом: рак возникает двумя путями: при отложении смол и без отложения смол. Если мы заставим кого-либо курить, вероятности этих двух состояний будут соответственно P (смола | do (курение)) и P (отсутствие смолы | do (отсутствие курения)). Однако, если возникнет состояние отсутствия смолы, вероятность рака будет P (рак | do (отсутствие смолы)). Оценив оба сценария по их относительным вероятностям при do (курение), получится рассчитать общую вероятность возникновения рака по причине курения. Те же аргументы действуют, если мы не даем кому-либо курить, — do (отсутствие курения). Разница между результатами дает нам среднее каузальное воздействие курения по сравнению с воздержанием от него на возникновение рака. Как я только что объяснил, мы оцениваем каждую из двух do-вероятностей, обсужденных выше, прямо из данных, т. е. записываем их математически в терминах вероятностей, не использующих оператор do. Таким образом, математика делает для нас то, чего не могли добиться десятилетия споров и свидетельств конгрессов, — количественно оценить каузальное воздействие курения на рак, конечно, при условии, что наши предположения верны.

Процесс, который я только что представил, описывающий вероятность P (рак | (курение)) в терминах вероятностей, исключающих оператор do, называется поправкой парадного входа. От поправки черного хода он отличается тем, что мы вносим поправки для двух переменных (курение и смола) вместо одной, и эти переменные лежат на прямом пути от курения к раку, а не на пути через черный ход. Для читателей, знакомых с математическим языком, я покажу эту формулу, которой нет в обычных учебниках статистики. Здесь X — это курение, Y — рак, Z — смола, а U (которое подозрительно отсутствует в формуле) — это ненаблюдаемая переменная, ген курильщика:

Читателям со вкусом к математике будет интересно сравнить эту формулу с формулой для поправки черного хода, которая записывается так:

Даже для читателей, совсем не владеющих математическим языком, можно сделать несколько интересных замечаний об уравнении (2). Первое и самое важное: в нем нигде нет переменной U (ген курильщика). Весь ее смысл как раз в этом. Мы успешно сняли осложнения по U, не обладая никакими данными по ней. Для любого статистика поколения Фишера это выглядело бы как самое настоящее чудо. Во-вторых, в самом начале, во введении, я рассказывал про эстиманд как способ вычислить интересующую нас величину в рамках данного вопроса. Уравнения (2) и (3) — самые сложные и интересные эстиманды в этой книге. Левая сторона представляет вопрос «Каково воздействие X на Y?» Правая сторона — это эстиманд, способ ответа на заданный вопрос. Обратите внимание, что эстиманд не содержит никаких do, только see, представленные вертикальными чертами, и это означает, что его можно рассчитать по имеющимся данным.

К этому моменту, я уверен, многие читатели гадают, насколько этот вымышленный сценарий близок к реальности. Неужели жаркий спор о курении и раке разрешился благодаря одной работе на основе наблюдений и одной каузальной диаграмме? Если мы предположим, что рис. 41 точно отражает причинностный механизм возникновения рака, ответом будет абсолютное «да». Однако то, насколько наши допущения справедливы для реального мира, требует дополнительного обсуждения.

Дэвид Фридман, мой старый друг, занимающийся статистикой в Калифорнийском университете в Беркли, серьезно раскритиковал меня по этому вопросу. Он утверждает, что модель на рис. 41 нереалистична по трем причинам. Во-первых, если ген курильщика» существует, он должен влиять и на то, как тело избавляется от чужеродных веществ в легких, и, таким образом, люди с этим геном будут более склонны к возникновению отложений смол, а люди, лишенные его, — более устойчивы к нему. Поэтому он бы нарисовал стрелку от гена курильщика к смоле, и в этом случае формула парадного входа окажется непригодной. Фридман считает также маловероятным, чтобы курение влияло на возникновение рака только через отложения смол. С уверенностью можно предположить и другие механизмы: не исключено, что курение ведет к хроническому воспалению, которое, в свою очередь, способствует развитию рака. Наконец, говорит он, отложения смол в легких живого человека все равно нельзя измерить со сколь-либо приемлемой точностью, поэтому предложенную мной работу на основе наблюдений не провести в реальном мире.

Я не возражаю против критики Фридмана в этом конкретном примере. Я не специалист по раку, и мне всегда придется оставлять на усмотрение эксперта в данном вопросе, насколько подобная диаграмма адекватно отражает процессы, происходящие в реальном мире. На самом деле одно из самых значительных достижений метода каузальных диаграмм в том, что они делают допущения прозрачными и открытыми для обсуждения экспертами и политиками.

Тем не менее цель моего примера была не в том, чтобы предложить новый механизм для воздействия курения на организм, а в том, чтобы продемонстрировать, как математика в определенной ситуации способна устранить воздействие конфаундеров, даже если данных по самому конфаундеру нет. Подобную ситуацию легко распознать. В ситуациях, когда каузальное воздействие X на Y осложняется одним набором переменных (С) и опосредуется другим (М) (рис. 42) и, более того, опосредующие переменные защищены, как щитом, от воздействий C, вы всегда можете оценить воздействие X, пользуясь наблюдаемыми данными. Узнав об этом факте, ученым было бы разумно, столкнувшись с неустранимыми конфаундерами, искать защищенные медиаторы. Как говорил Луи Пастер, «удача сопутствует подготовленному уму».

К счастью, достоинства поправок парадного входа не остались не оцененными. В 2014 году Адам Глинн и Константин Кашин, оба политологи из Гарварда (Глинн впоследствии перешел в Университет Эмори), написали получившую премию работу, которую следовало бы сделать обязательным чтением для всех ученых, занимающихся исчислениями в области общественных наук. Они применили новый метод к массиву данных, ранее тщательно изученных представителями общественных наук, — исследованию по Закону о партнерстве в области профессиональной подготовки (Job Training Partnership Act; JTPA), которое проводилось с 1987 по 1989 год. По результатам JTPA 1982 года, Департамент труда создал программу профессиональной подготовки, которая, помимо других целей, снабжала участников профессиональными навыками, навыками поиска работы и опытом работы. Она собирала данные о людях, подававших заявки для участия в этой программе, тех, кто реально пользовались ее услугами, и об их доходах за последующие 18 месяцев. Следует обратить внимание, что в исследование входили и РКИ, и данные, полученные в результате наблюдений, в которых люди делали выбор самостоятельно.

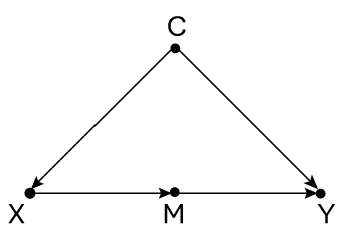
Рис. 42. Базовые условия для применения критерия парадного входа

Глинн и Кашин не рисовали каузальных диаграмм, но, судя по описанию их исследования, я бы нарисовал ее так, как на рис. 43. Переменная записавшиеся сообщает, зарегистрировался ли испытуемый для участия в программе или нет; переменная посещавшие сообщает, посещали ли записавшиеся занятия на самом деле. Очевидно, что программа могла повлиять на доходы только в том случае, если пользователь действительно посещал занятия, поэтому отсутствие прямой стрелки от записавшихся к доходам легко понять.

Глинн и Кашин не стали вдаваться в природу осложнителей, но я просуммировал их в переменной мотивация. Ясно, что человек, испытывающий сильную мотивацию увеличить свои доходы, с большей вероятностью запишется на курсы. Этот же человек с большей вероятностью увеличит свой заработок через 18 месяцев, вне зависимости от того, посещал ли он курсы. Цель исследования, конечно, — отделить влияние этого осложняющего фактора и найти, насколько велика помощь непосредственно от курсов.

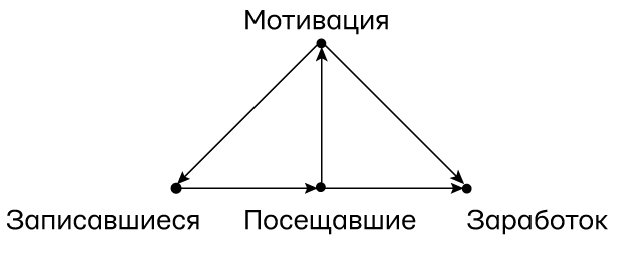
Рис. 43. Каузальная диаграмма для исследования JTPA

Сравнивая рис. 42 и 43, мы увидим, что критерий парадного входа был бы здесь применим, если бы не было стрелки от мотивации к посещавшим — щита, упомянутого выше. Во многих случаях мы оправдываем отсутствие такой стрелки. Например, если бы услуги программы осуществлялись только в назначенное время и люди не укладывались в него только по уважительным причинам, не связанным с мотивацией (скажем, забастовка водителей общественного транспорта или сломанная нога), мы могли бы стереть эту стрелку и воспользоваться критерием парадного входа.

В реальных условиях исследования, когда услуги программы доступны в любое время, подобный аргумент не годится. Тем не менее — и это особенно интересно — Глинн и Кашин протестировали критерий парадного входа. Отнесемся к этому как к тесту на сенситивность. Если мы подозреваем, что средняя стрелка обозначает очень слабое воздействие, искажение, возникающее, если считать ее отсутствующей, совсем незначительно. Судя по их результатам, именно так дело и обстояло. Приняв определенные разумные допущения, Глинн и Кашин получили неравенства, по которым определили, была ли поправка чрезмерной или недостаточной и насколько. Наконец, они сравнили предсказания черного хода и парадного входа с результатами рандомизированного контролируемого исследования, которое проводилось в то же самое время. Результаты впечатлили. Оценки с помощью критерия черного хода (с поправками по таким известным конфаундерам, как возраст, раса и регион) оказались совершенно неверны, они отличались от экспериментальных результатов на сотни тысяч долларов. Это именно та картина, которая наблюдается, если имеется нераспознанный конфаундер. Критерий черного хода не способен внести по нему поправки. Тем не менее оценки парадного входа убрали почти все воздействия со стороны переменной мотивация. Для мужчин оценки по критерию парадного входа оказались в пределах экспериментальной ошибки РКИ, даже с небольшой положительной ошибкой, предсказанной Глинном и Кашиным. Для женщин результаты былиь еще точнее. Оценки парадного входа совпали с экспериментальными данными почти идеально, без сколько-нибудь заметной ошибки. Работа Глинна и Кашина подтверждает как эмпирически, так и экспериментально, что, если только воздействие С на М (на рис. 42) незначительно, поправки парадного входа могут дать разумно точную оценку воздействия X на Y. Результат при этом значительно лучше, чем если вовсе не вводить поправок по С.

Изыскания Глинна и Кашина показывают, почему поправки парадного входа оказываются столь мощным инструментом: он позволяет нам снимать осложнения по таким переменным, по которым мы не можем получить наблюдений (например, в случае мотивации), включая те, которые даже не можем никак назвать. Рандомизированные контролируемые исследования считаются золотым стандартом оценок каузального воздействия ровно по тем же причинам. Поскольку оценки парадного входа равноценны, к тому же обладают дополнительным преимуществом, позволяя наблюдать поведение людей в их привычной обстановке, а не в условиях лаборатории, я не удивлюсь, если когда-нибудь этот метод составит серьезную конкуренцию РКИ.