Теперь, когда мы показали, что телепродюсеры не обладают навыками телепатии и монеты не могут общаться друг с другом, мы можем развенчать еще несколько мифов. Давайте начнем с мифа о «плохом / плохом / хорошем» лекарстве.

Представим себе доктора (назовем его «доктор Симпсон»), который сидит в кабинете и читает о многообещающем новом препарате (лекарстве D), который вроде бы сокращает риск сердечного приступа. С радостным предвкушением он изучает данные исследователей в Интернете. Однако радость убавляется, когда он смотрит на данные о пациентах-мужчинах и замечает, что, если они принимают препарат, риск получить сердечный приступ, вообще-то, повышается. «Ага, — говорит он, — вероятно, лекарство D очень эффективно для женщин».

Но потом он переходит к следующей таблице, и разочарование сменяется изумлением. «Что это? — восклицает доктор Симпсон. — Тут значится, что у женщин, которые принимали лекарство D, тоже повысился риск сердечного приступа. Кажется, у меня едет крыша! Получается, лекарство вредно для женщин и вредно для мужчин, но полезно людям в целом».

Вы тоже пришли в недоумение? Если так, вы в хорошей компании. Этот парадокс, который впервые описал реальный статистик по имени Эдвард Симпсон в 1951 году, не давал покоя ученым более 60 лет и продолжает тревожить их до сих пор. Даже в 2016 году, когда я писал эту книгу, вышло четыре новые работы (включая диссертацию), в которых парадокс Симпсона пытались объяснить с четырех разных точек зрения.

В 1983 году Мелвин Новик написал: «Напрашивается вот такой ответ: если мы знаем, что пациент — мужчина или что пациент — женщина, нам не стоит использовать этот препарат. Но если пол неизвестен, препарат лучше использовать! Очевидно, что подобный вывод смехотворен». Я полностью согласен. Считать, что лекарство вредно для мужчин и вредно для женщин, но при этом полезно для людей, было бы действительно смехотворно. Итак, одно из этих трех утверждений должно быть неверным. Но какое? И почему? И как вообще возможна эта путаница?

Чтобы ответить на эти вопросы, нам, конечно, нужно взглянуть на (вымышленные) данные, которые так сильно озадачили нашего доктора Симпсона. Исследование было наблюдательным, а не рандомизированным, с участием 60 мужчин и 60 женщин. Это означает, что пациенты сами решали, принимать препарат или нет. В табл. 8 показано, сколько представителей каждого пола получали препарат D и у скольких впоследствии был диагностирован сердечный приступ.

Позвольте мне подчеркнуть, в чем именно заключается парадокс. Как вы можете видеть, 5,0 % (1 из 20) женщин в контрольной группе пережила сердечный приступ, в то время как в группе женщин, принявших лекарство, этот показатель составил 7,5 %, т. е. лекарство связано с риском сердечного приступа у женщин. У мужчин сердечный приступ случился у 30 % в контрольной группе и у 40 % в группе принявших лекарство. Значит, лекарство связано с риском сердечного приступа у мужчин. Доктор Симпсон был прав.

Таблица 8. Вымышленные данные, иллюстрирующие парадокс Симпсона

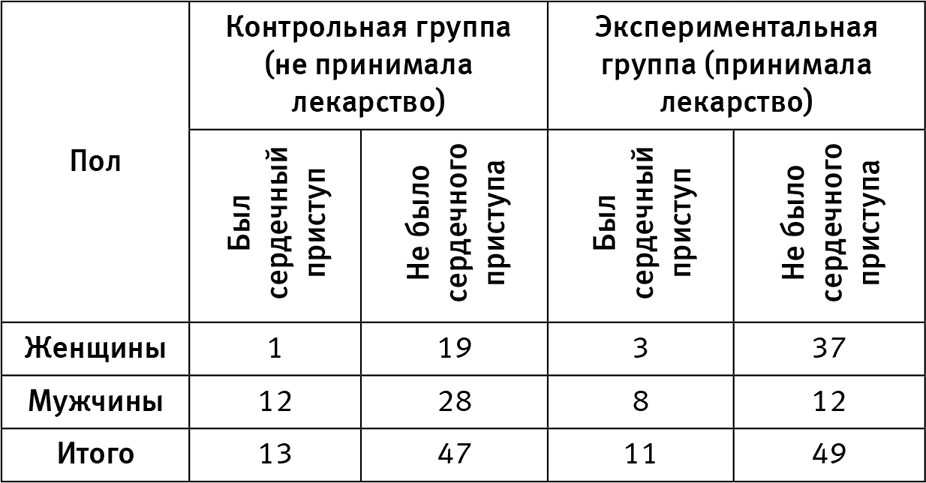
Но теперь посмотрите на третью строку таблицы. В контрольной группе сердечный приступ был у 22 %, а в группе принявших лекарства — у 18 %. Итак, если судить по итогам эксперимента, препарат D, похоже, снижает риск сердечного приступа у населения в целом. Добро пожаловать в загадочный мир парадокса Симпсона!

Почти 20 лет я пытаюсь убедить научное сообщество в том, что парадокс Симпсона ставит нас в тупик из-за неправильного применения законов причинности к статистическим соотношениям. Если использовать причинно-следственные обозначения и диаграммы, то можно четко и однозначно решить, предотвращает ли препарат D сердечные приступы или вызывает их. По сути, парадокс Симпсона — это загадка, связанная с конфаундерами, и ее реально решить теми же методами, которые мы уже использовали в похожем случае. Любопытно, что авторы трех из четырех работ 2016 года, о которых я упомянул, продолжают сопротивляться этому решению.

Любая попытка разрешить парадокс (особенно если ему уже несколько десятилетий) должна соответствовать базовым критериям. Во-первых, как я сказал выше в связи с парадоксом Монти Холла, ей следует объяснить, почему люди находят парадокс удивительным или невероятным. Во-вторых, ей нужно показать тип сценариев, в которых возможно его появление. В-третьих, когда парадокс все-таки возникает, и нам надо сделать выбор между двумя правдоподобными, но противоречивыми утверждениями, важно указать, какое из утверждений является правильным.

Давайте начнем с вопроса, почему парадокс Симпсона вызывает удивление. Чтобы ответить на него, надо провести различие между двумя вещами — инверсией Симпсона и парадоксом Симпсона.

Инверсия Симпсона — это чисто числовое явление: как видно из табл. 7, это изменение относительной частоты какого-то события в двух или более различных выборках при объединении выборок. В нашем примере мы увидели, что 3/40 > 1/20 (частота сердечных приступов среди женщин, принимавших и не принимавших лекарство D) и 8/20 > 12/40 (частота среди мужчин). Тем не менее, когда мы объединили показатели женщин и мужчин, неравенство изменило направление на противоположное: (3 + 8) / (40 + 20) < (1 + 12) / (20 + 40). Если вы считали такой поворот математически невозможным, то, скорее всего, неверно применяли или неверно запомнили свойства дробей. Многие люди, кажется, считают, что если A/B > a/b и C/D > c/d, то (A + C) / (B + D) > (a + c) / (b + d). Но это общее представление ошибочно. Только что приведенный нами пример его опровергает.

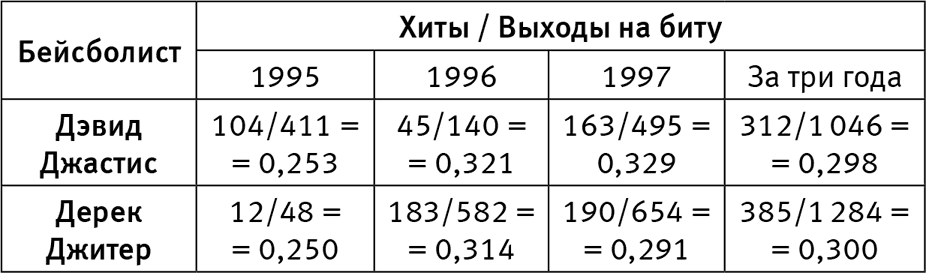
Инверсию Симпсона можно обнаружить в наборах данных из реальной жизни. Вот прекрасный образец для фанатов бейсбола, касающийся двух звездных бейсболистов — Дэвида Джастиса и Дерека Джитера. В 1995 году у Джастиса был более высокий средний показатель: 0,253 против 0,250. В 1996 году у Джастиса снова был более высокий средний показатель 0,321 против 0,314. А в 1997 году он набрал больше очков, чем Баттер, третий сезон подряд: 0,329 против 0,291. Тем не менее за три сезона вместе взятых больше очков оказалось у Джитера! Табл. 8 демонстрирует расчеты для читателей, которые хотели бы их проверить.

Как один игрок может быть хуже, чем другой, в 1995, 1996 и 1997 годах, но лучше в течение трехлетнего периода? Эта инверсия напоминает о лекарстве из нашего примера. На самом деле это невозможно; все дело в том, что мы использовали слишком простое слово («лучше») для описания сложного процесса усреднения по разным сезонам. Обратите внимание, что выходы на биту (знаменатели) не распределяются равномерно по годам. В 1995 году у Джитера было их очень мало, поэтому его довольно низкий средний показатель в этом году мало повлиял на общий средний показатель. Однако у Джастиса было намного больше выходов на биту в его наименее продуктивном году, 1995-м, и это привело к снижению общего среднего показателя. Как только вы поймете, что «лучший нападающий» определяется соперничеством лицом к лицу, а средневзвешенным значением, которое учитывает, как часто играл каждый из них, думаю, все это будет уже не так удивительно.

Таблица 8. Данные (невымышленные), иллюстрирующие инверсию Симпсона

Инверсия Симпсона, конечно же, удивляет некоторых людей и даже фанатов бейсбола. Каждый год у меня появляются студенты, которые сначала не могут поверить в такие вещи. Но потом они идут домой, работают над подобными примерами и утрачивают сомнения. Просто они начинают по-новому, немного глубже понимать, как работают числа (и особенно агрегированные показатели). Я не называю инверсию Симпсона парадоксом, потому что это по большому счету вопрос исправления ошибочных представлений о том, как ведут себя средние значения. Парадокс — нечто большее: он должен повлечь за собой конфликт между двумя глубоко укоренившимися убеждениями.

У профессиональных статистиков, которые работают с числами каждый день своей жизни, еще меньше оснований считать инверсию Симпсона парадоксом. Простое арифметическое неравенство не могло бы озадачить и увлечь их до такой степени, чтобы они продолжали писать о нем статьи 60 лет спустя.

Вернемся теперь к нашему основному примеру — парадоксу с лекарством. Я объяснил, почему три утверждения («вредно для мужчин», «вредно для женщин» и «полезно для людей), интерпретируемые как увеличение и уменьшение пропорций, не противоречат друг другу математически. И все же вам может показаться, что это физически невозможно. Странно, что лекарство способно вызвать одновременно у меня и у вас сердечный приступ, но в то же время предотвратить сердечный приступ у нас обоих. Это интуитивное чувство универсально; оно появляется у нас в двухлетнем возрасте, задолго до того, как мы начинаем изучать числа и дроби. Поэтому я думаю, вы испытаете облегчение, узнав, что не нужно отказываться от интуиции. Лекарства с такими свойствами пока не изобрели и не изобретут никогда, что мы можем доказать математически.

Первым внимание к этому интуитивно очевидному принципу привлек статистик Леонард Сэвидж. В работе 1954 года он назвал его «верное дело». Он писал: «Бизнесмен задумывается о покупке определенного объекта недвижимости. При этом он учитывает исход следующих президентских выборов. Чтобы прояснить этот вопрос, он спрашивает себя, купил бы он этот объект, если бы знал, что выиграет кандидат-демократ, и приходит к выводу, что да. Потом он задает тот же вопрос о кандидате-республиканце и приходит к такому же выводу. Осознав, что покупка состоялась бы в любом случае, он решается на нее, несмотря на то, что не знает, кто победит. Очень редко решение может быть принято на основе этого принципа, но… Я не знаю другого экстралогического принципа, управляющего решениями, который было бы так легко принять».

Замечание Сэвиджа в конце цитаты особенно проницательно: он понимает, что принцип верного дела экстралогический. Более того, если интерпретировать его верно, окажется, что он основан на причинно-следственной, а не классической логике. Кроме того, он говорит, что «не знает иного… принципа, который». Очевидно, что он говорил о нем со многими людьми, и они нашли подобное рассуждение очень убедительным.

Чтобы связать принцип верного дела у Сэвиджа с обсуждением выше, предположим, что на самом деле выбор стоит между двумя объектами недвижимости — A и B. Если победит демократ, у бизнесмена есть 5 %-ный шанс заработать доллар на объекте A и 8 %-ный шанс заработать доллар на объекте B. Таким образом, B предпочтительнее A. Если выиграет республиканец, у него есть 30 %-ный шанс заработать доллар на объекте A и 40 %-ный шанс заработать доллар на объекте B. И снова В оказывается предпочтительнее А. Согласно принципу верного дела, ему точно нужно купить объект B. Но наблюдательные читатели заметят, что числовые величины здесь такие же, как и в истории Симпсона, а значит, покупка объекта B может оказаться поспешным решением.

Более того, аргумент, приведенный выше, содержит очевидный недостаток. Если решение бизнесмена купить недвижимость способно повлиять на исход выборов (например, если за его действиями следили СМИ), то покупка недвижимости А окажется в его интересах. А вред от избрания не того президента перевесит любую финансовую выгоду от сделки, когда президент уже будет выбран.

Чтобы принцип верного дела проявил себя, мы должны утвердиться в том, что решение бизнесмена не повлияет на исход выборов. Если бизнесмен уверен, что его решение не окажет воздействия на вероятность победы демократов или республиканцев, он может спокойно покупать недвижимость В.

Обратите внимание, что отсутствующий ингредиент (который Сэвидж не указал явно) — предположение о причине. Правильная версия его принципа будет выглядеть так: действие, которое, по нашему предположению, повышает вероятность некоего результата и в том случае, если событие С произошло, и в том случае, если оно не произошло, повысит его вероятность также и в случае, когда мы не знаем, произошло ли С… при условии, что само действие не изменит вероятность C. В частности, не существует такого понятия, как «хорошее / хорошее / плохое» лекарство. Этот исправленный вариант принципа Сэвиджа не вытекает из классической логики: чтобы доказать его, понадобится причинное исчисление с привлечением оператора do. Наша сильная интуитивная убежденность в невероятности такого лекарства предполагает, что люди (а также машины, запрограммированные на подражание человеческим мыслям) используют что-то вроде do-исчисления для направления интуиции.

В соответствии с исправленным принципом, одно из следующих трех утверждений должно быть ложным: препарат D повышает вероятность сердечного приступа у мужчин и женщин; препарат D снижает вероятность сердечного приступа у населения в целом; препарат не меняет количество мужчин и женщин. Поскольку крайне маловероятно, что лекарство может изменить пол пациента, одно из первых двух утверждений должно быть ложным.

Какое же? Не стоит искать подсказок в табл. 7. Чтобы ответить на этот вопрос, нужно рассмотреть не только данные, но и как они были получены. Как всегда, обсудить этот процесс без диаграммы причинности просто невозможно.

Диаграмма на рис. 44 учитывает важную информацию: препарат не влияет на пол пациента; пол влияет на риск сердечного приступа (у мужчин риск выше); пациент решил принять лекарство D или отказался от него. В этом эксперименте женщины явно предпочитали принимать D, а мужчины чаще от него отказывались. Таким образом, пол — осложняющая переменная, влияющая и на лекарство, и на сердечный приступ. Чтобы объективно оценить, как лекарство влияет на сердечный приступ, нужно сделать поправку на конфаундер. Для этого надо рассмотреть данные по мужчинам и женщинам отдельно, а затем — взяв среднее значение:

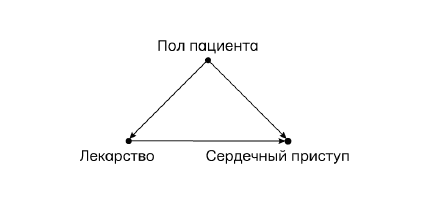
Рис. 42. Диаграмма причинности для примера с парадоксом Симпсона

В группе женщин сердечный приступ случился у 5,0 % не принимавших лекарство D и у 7,5 % принимавших лекарство.

В группе мужчин сердечный приступ случился у 30 % принимавших лекарство D и у 40 % принимавших лекарство.

В среднем (поскольку мужчины и женщины встречаются одинаково часто) сердечный приступ случился у 17,50 % не принимавших лекарство D (среднее между 5 и 30) и у 23,75 % принимавших лекарство (среднее между 7,5 и 40).

Это четкий и недвусмысленный ответ, который мы искали. Лекарство D нельзя назвать «плохим / плохим / хорошим» — оно «плохое / плохое / плохое» — для мужчин, женщин и людей в целом.

Я не хочу, чтобы из этого примера у вас создалось впечатление, что агрегировать данные всегда неверно, а разделять их всегда верно. Все зависит от процесса, который произвел данные. В парадоксе Монти Холла мы увидели, что, изменив правила игры, мы также изменили ее исход. Тот же принцип работает и здесь. Я использую другую историю, чтобы продемонстрировать, когда объединение данных окажется уместным. Хотя данные будут абсолютно такими же, роль скрытой третьей переменной изменится, и то же произойдет с результатом.

Давайте начнем с предположения о том, что лекарство В снижает артериальное давление (АД), повышение которого, как известно, может привести к сердечному приступу. Естественно, исследователи лекарства В хотели увидеть, не понизит ли оно риск сердечного приступа, поэтому они измеряли артериальное давление пациентов после приема лекарства, а не только фиксировали, был ли у них сердечный приступ.

Табл. 9 показывает данные из исследования лекарства В. Она вам знакома: в ней те же показатели, что и в табл. 7. Тем не менее вывод будет абсолютно противоположным.

Таблица 9. Вымышленные данные для примера с артериальным давлением

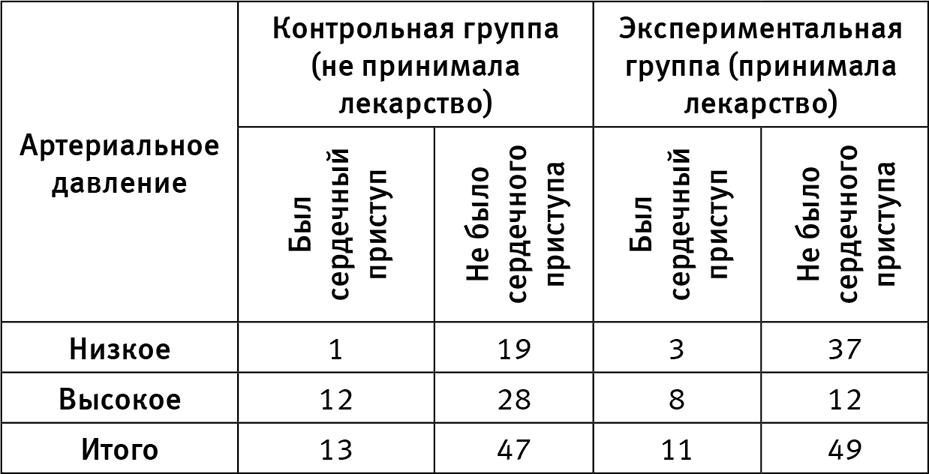
Как видите, прием лекарства В оказал эффект: в экспериментальной группе давление понизилось у вдвое большего числа человек (у 40 из 60 по сравнению с 20 из 60 в контрольной группе). Другими словами, оно сделало в точности то, что должно делать лекарство против сердечного приступа. Оно вывело людей из категории высокого риска в категорию более низкого риска. Этот фактор перевешивает все остальное, и мы можем прийти к обоснованному выводу о том, что часть табл. 9 с агрегированной информацией дает нам верный результат.

Как обычно, диаграмма причинности все прояснит и позволит нам вывести результат механически, даже не думая о данных и о том, понижает или повышает это лекарство наше кровяное давление. В этом случае скрытая третья переменная — артериальное давление, и диаграмма выглядит, как показано на рис. 43. Здесь артериальное давление — скорее посредник, чем вмешивающийся фактор. Один взгляд на диаграмму показывает, что на взаимосвязь лекарства и сердечного приступа не действует конфаундер (т. е. нет черного хода), поэтому стратификация данных не требуется. Более того, если учитывать только артериальное давление, мы исключим один из каузальных путей (возможно, основной) для действия лекарства. По обеим этим причинам наш вывод прямо противоположен выводу для препарата D: препарат B работает и совокупные данные подтверждают этот факт.

С исторической точки зрения примечательно, что Симпсон в статье 1951 года, которая вызвала всю эту шумиху, сделал то же самое, что и я. Он представил две истории с абсолютно одинаковыми данными. В одном примере было интуитивно понятно, что агрегирование данных оказалось, как он выразился, «разумной интерпретацией»; в другом более разумным стало разделение данных. Итак, Симпсон понял, что это парадокс, а не просто инверсия. Однако он не предложил никакого решения, кроме как использовать здравый смысл. И самое важное: он не предположил, что, если история содержит дополнительную информацию, которая позволяет различить «разумное» и «неразумное», возможно, статистикам стоит учесть ее при анализе.

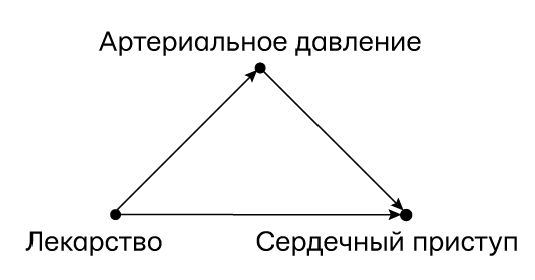
Рис. 43. Диаграмма причинности для примера с парадоксом Симпсона (второй вариант)

Деннис Линдли и Мелвин Новик рассмотрели это предположение в 1981 году, но не смогли примириться с гипотезой, что правильное решение зависит от причинной истории, а не от данных. Они признали: «Мы могли бы использовать язык причинно-следственных связей… Мы решили этого не делать и вообще не обсуждать причинность, потому что, хотя это понятие широко используется, у него как будто нет четкого определения». Так они обобщили фрустрацию пяти поколений статистиков, которые понимали, что информация о причинно-следственных связях чрезвычайно необходима, но язык для ее выражения безнадежно отсутствует. В 2009 году, за четыре года до смерти в возрасте 90 лет, Линдли признался мне, что он не написал бы приведенные выше слова, если бы моя книга была доступна в 1981 году.

Некоторые читатели моих книг и статей предположили, что правило, регулирующее агрегирование и разделение данных, основывается на временном приоритете в обработке и скрытой третьей переменной. Они утверждают, что в случае с артериальным давлением данные необходимо агрегировать, потому что измерение давления происходит после того, как пациент принимает лекарство, но в случае с полом данные нужно стратифицировать, потому что пол пациента определен заранее. Хотя это правило работает во многих случаях, его нельзя считать универсальным. Простой случай — M-тип (игра 4 в главе 4). Здесь B может предшествовать A; тем не менее мы все равно не должны ставить условие на B, потому что это нарушит критерий черного хода. Мы должны обратиться к причинно-следственной структуре рассказа, а не к временной информации.

Наконец, вы можете задаться вопросом, возможен ли парадокс Симпсона в реальном мире. Ответ будет положительным. Конечно, он встречается недостаточно часто, чтобы статистики наблюдали его ежедневно, однако он не совсем неизвестен и, вероятно, происходит чаще, чем об этом сообщают статьи в научных журналах. Вот два задокументированных случая.

Наблюдательное исследование, опубликованное в 1996 году, показало, что открытая операция по удалению камней в почках чаще завершалась успехом, чем эндоскопическая операция, которую, делали при небольших камнях. Кроме того, оно продемонстрировало, что, если камни в почках были больше, повышался и процент успеха. Но в целом для открытой операции он был ниже. Как и в нашем первом примере, выбор метода лечения зависел от состояния пациента: если камни были крупнее, открытая хирургическая операция была вероятнее, но прогноз оказывался хуже.

В исследовании заболеваний щитовидной железы, опубликованном в 1995 году, курильщики продемонстрировали более высокий коэффициент выживания (76 %) в течение 20 лет, чем некурящие участники (69 %). Но у некурящих этот показатель был выше в шести из семи возрастных групп, а в седьмой разница оказалось минимальной. Фактор возраста явно повлиял и на курение, и на выживание: средний курильщик был моложе среднего некурящего (возможно, потому что курильщики старшего возраста уже умерли). Разделив данные по возрастным группам, мы пришли к выводу, что курение отрицательно влияет на выживание.

Поскольку парадокс Симпсона настолько плохо поняли, некоторые статистики специально стараются его избежать. Слишком часто они пытаются бороться с симптомом, инверсией Симпсона, ничего не делая с болезнью — конфаундерами. Вместо того чтобы подавлять симптомы, необходимо обращать на них внимание. Парадокс Симпсона предупреждает нас о случаях, когда по крайней мере один из статистических трендов (в агрегированных данных, разделенных или в тех и других) не может отражать причинно-следственное влияние. Есть, конечно, и другие тревожные знаки. Если оценить причинно-следственный эффект в совокупности, получившаяся величина, к примеру, может оказаться выше, чем каждая аналогичная величина в каждой страте. И снова приходится повторять: этого не должно произойти, если мы должным образом учли вмешивающиеся факторы. Однако по сравнению с такими признаками инверсию Симпсона труднее игнорировать именно потому, что это разворот, качественное изменение знака. Идея вредного / вредного / полезного препарата вызовет недоверие даже у трехлетнего ребенка — и совершенно справедливо.