В 1946 году Джозеф Берксон, биостатистик из клиники Мэйо, указал на интересную особенность, которую выявили наблюдения в условиях больницы: даже если два заболевания не связаны друг с другом у населения в целом, они могут показаться связанными у пациентов.

Чтобы понять суть этого наблюдения, давайте начнем с диаграммы причинности (рис. 34). Также полезно подумать об экстремальном варианте: ни болезнь 1, ни болезнь 2 обычно недостаточно серьезны, чтобы привести к госпитализации, но их сочетания достаточно. В этом случае мы ожидаем, что болезнь 1 будет сильно коррелировать с болезнью 2 у госпитализированных людей.

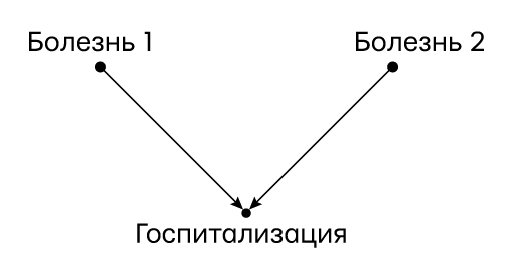
Рис. 34. Диаграмма причинности для парадокса Берксона

Исследуя пациентов в больнице, мы учитываем только госпитализированных людей. Как мы знаем, ограничив себя коллайдером, мы создаем ложную связь между болезнью 1 и болезнью 2. Во многих предыдущих примерах ассоциация была отрицательной из-за эффекта поверхностного объяснения, но здесь она положительна, потому что для госпитализации требуются оба заболевания (не только одно).

Однако эпидемиологи долгое время отказывались верить в такую возможность. Они игнорировали ее до 1979 года, когда Дэвид Сакетт из Университета Макмастера, эксперт по всевозможным статистическим ошибкам, представил убедительные доказательства того, что парадокс Берксона реален. В одном примере (табл. 7) он изучил две группы заболеваний: респираторные и костные. Около 7,5 % людей в общей популяции страдают заболеваниями костей, и этот процент не зависит от того, есть ли у них респираторные заболевания. Но для госпитализированных людей с респираторными заболеваниями частота заболеваний костей возрастает до 25 %! Сакетт назвал это явление систематической ошибкой при поступлении в больницу, или систематической ошибкой Берксона.

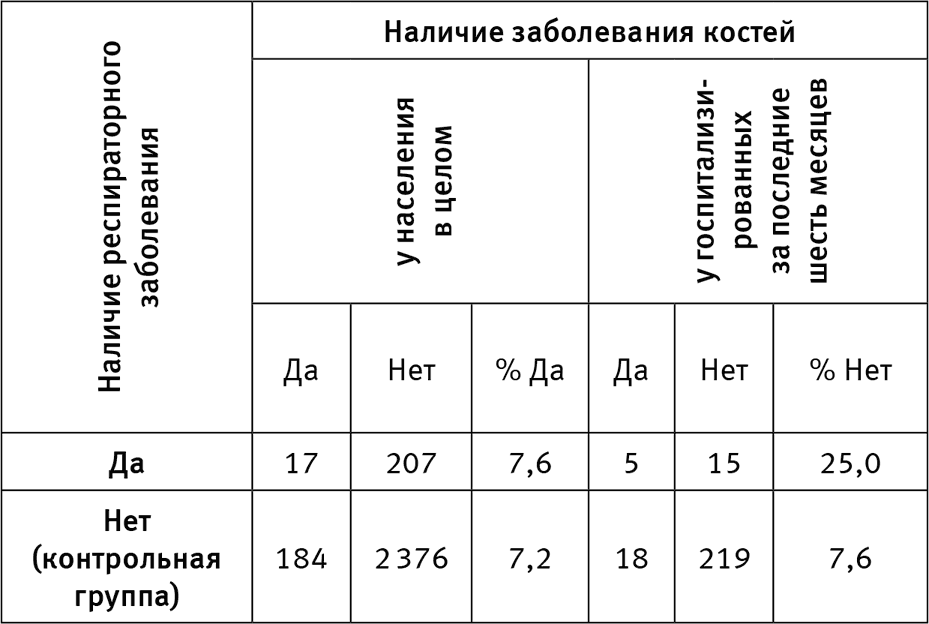
Таблица 7. Данные Сакетта, иллюстрирующие парадокс Берксона

Сакетт признает, что мы не вправе окончательно приписать этот эффект систематической ошибке Берксона, потому что возможны вмешивающиеся факторы. Споры в том или ином виде продолжаются до сих пор. Однако, в отличие от 1946 и 1979 годов, сегодня эпидемиологи понимают причинно-следственные диаграммы и знают, какие систематические ошибки они демонстрируют. Сегодня обсуждаются более тонкие моменты: насколько велика может быть ошибка и достаточно ли она масштабна, чтобы быть замеченной на диаграммах причинности с большим количеством переменных. Это прогресс!

Корреляции, вызванные коллайдером, не новы. Они обнаружились в исследовании, проведенном в 1911 году английским экономистом Артуром Сесилом Пигу, который сравнивал детей, родившихся у алкоголиков и неалкоголиков. Также они встречаются, хотя под другими названиями, в работах Барбары Бёркс (1926), Герберта Саймона (1954) и, конечно же, Берксона. Кроме того, они вовсе не такие эзотерические, как может показаться на моих примерах. Попробуйте такой эксперимент: подбросьте две монеты одновременно 100 раз, но записывайте результаты только тогда, когда хотя бы одна из них выпадет орлом. Посмотрев на таблицу, в который, вероятно, будет около 75 записей, вы обнаружите, что результаты двух одновременных подбрасываний не окажутся независимыми. Каждый раз, когда первая монета выпадала решкой, вторая выпадала орлом. Как это получилось? Неужели монеты общались друг с другом со скоростью света? Конечно нет. На самом деле вы ограничили себя коллайдером, отбросив все результаты «решка — решка».

В книге «Направление времени», опубликованной посмертно в 1956 году, философ Ханс Райхенбах высказал смелую гипотезу, названную принципом общего дела. Опровергая утверждение «Корреляция не подразумевает причинно-следственной связи», Райхенбах выдвинул далеко идущую идею: «Нет корреляции без причинно-следственной связи». Он имел в виду, что корреляция между двумя переменными, X и Y, не может возникнуть случайно. Либо одна из переменных вызывает другую, либо третья переменная, например Z, предшествует и вызывает их обе.

Наш простой эксперимент с подбрасыванием монеты доказывает, что утверждение Райхенбаха пошло слишком далеко, потому что в нем не учитывается процесс отбора наблюдений. У результата для двух монет не было общей причины, и ни одна не сообщала другой, что получилось у нее. Тем не менее между результатами в нашем списке возникла корреляция. Ошибка Райхенбаха заключалась в том, что он не учел структуру коллайдера, на основе которой отбирались данные. Ошибка оказалась особенно показательной, потому что она указывает на конкретный изъян в принципах работы нашего мозга. Мы живем так, как если бы принцип общей причины соблюдался. Когда мы видим такие закономерности, мы ищем причинное объяснение. Более того, мы жаждем объяснений, которые показали бы нам стабильные механизмы за рамками данных. Больше всего нам подходит объяснение через прямую причинность: X вызывает Y. Когда оно не подходит, обычно нас удовлетворяет общая причина для X и Y. Коллайдеры слишком призрачны, чтобы удовлетворить эти причинные аппетиты. Мы все еще хотим узнать механизм, как две монеты координируют свое поведение. Ответ вызывает у нас полное разочарование: они вообще не общаются.

Наблюдаемая нами корреляция — иллюзия в чистейшем и буквальнейшем смысле. Или даже заблуждение, т. е. иллюзия, которую мы сами вызвали у себя, выбирая, какие события включить в отобранные данные, а какие проигнорировать. Важно понимать, что мы не всегда осознаем, что сделали этот выбор, и поэтому часто попадаем в ловушку, созданную ошибкой коллайдера. В эксперименте с двумя монетами выбор был осознанным: я просил не записывать результаты с двумя решками. Но во многих случаях мы не осознаем, что делаем выбор, или же выбор делается за нас. В парадоксе Монти Холла ведущий открывает нам дверь. В парадоксе Берксона неосторожный исследователь берет госпитализированных пациентов из соображений удобства, не осознавая, что таким образом искажает результаты исследования.

Искажающая призма коллайдера не менее распространена в повседневной жизни. Джордан Элленберг в книге «Как никогда не ошибаться» спрашивает: вы когда-нибудь замечали, что среди людей, с которыми вы встречались, привлекательные часто оказывались неприятными личностями? Вместо того чтобы строить сложные психосоциальные теории, рассмотрите простое объяснение. Ваш выбор партнеров все это время зависел от двух факторов: их привлекательности и личных качеств. Вы были готовы завязать отношения с неприятным, но привлекательным человеком или с приятным, но непривлекательным, и, конечно, с приятным и привлекательным. Но только не с неприятным и непривлекательным! То же явление мы наблюдали в примере с двумя монетами, когда вы подвергали цензуре результаты «орел или решка». Это явление создает ложную отрицательную корреляцию между привлекательностью и личностью. Но печальная правда заключается в том, что непривлекательные люди бывают неприятными так же часто, как привлекательные, однако вы никогда этого не узнаете, потому что никогда не станете встречаться с плохим и некрасивым человеком.