Глава 5. Уравнение влияния

Вы когда-нибудь задумывались о вероятности того, что вы – именно вы, а не кто-то еще? Я не имею в виду кого-то слегка другого – скажем, человека, который был (или не был) в Диснейленде или видел все (или не все) фильмы «Звездных войн». Нет, кто-то совсем другой: родившийся в другой стране или даже в другое время.

Население нашей планеты составляет примерно 8 миллиардов человек. Это означает, что вероятность оказаться конкретным человеком – примерно 1 к 8 миллиардам. Шансы угадать все номера в лотерее 6 из 49, которая проводится в Великобритании, равны примерно 1 к 14 миллионам, поэтому вероятность выиграть в такой лотерее по единственному билету в 570 раз выше, чем вероятность того, что вы – это вы.

Иногда я представляю себе Вселенную, в которой каждый день просыпаюсь случайным человеком. Вышеприведенные вычисления говорят: мы можем почти забыть о том, что дважды подряд проснемся собой (шансы на это тоже равны 1 на 8 миллиардов), но чему равна вероятность, что мы проснемся в том же городе, где заснули? В шведском Уппсале, где я живу, примерно 200 тысяч жителей. Значит, вероятность того, что я проснусь завтра здесь же, составляет всего около 1 / 40 000. Если я продолжу свое путешествие в течение пятидесяти лет, каждое утро просыпаясь случайным человеком, то шансы, что однажды снова окажусь в Уппсале, составляют примерно 50 %. Можно сказать, что подбрасывание монетки определит, увижу ли я снова восход в моем родном городе.

В своем случайном путешествии каждые два года я проводил бы день в Лондоне и день в Лос-Анджелесе. Нью-Йорк, Каир и Мумбаи посещал бы почти раз в год. Большой Токио с его населением 38 миллионов был бы моим домом почти дважды в год. Хотя вероятность проснуться в любом конкретном населенном пункте мала, у меня будет гораздо больше шансов оказаться в густонаселенных городских районах, чем в сельской местности. Больше всего шансов проснуться в Китае, затем в Индии. Если и можно найти какую-то стабильность во всей этой суматохе обитания в случайных телах, то она в этих двух странах. В совокупности в них проживает 2,8 миллиарда человек, поэтому примерно 2,5 дня в неделю я жил бы в одном из этих государств. В Африке окажусь примерно раз в неделю, а в США – чуть чаще раза в месяц. Мое путешествие, которое, вероятно, никогда не вернет меня в исходную точку, напоминает мне, что я одновременно и исключительно маловероятен, и до невозможности незначителен.

А теперь представьте, что я просыпаюсь не как человек, выбираемый наугад из всего населения планеты, а как один из тех, на кого подписан в Instagram. Я не активный пользователь этой социальной сети для фотографий и поэтому подписан только на нескольких френдов, которые нашли время, чтобы отыскать меня. Так что я проснусь одним из них: возможно, это будет школьный приятель или коллега-ученый из другого университета. Я получу на день их тело, узнаю, каково быть ими (возможно, даже отправлю какое-нибудь сообщение старому себе), а затем отправлюсь в постель и проснусь снова другим случайным человеком – одним из тех, на которых подписаны уже они.

Я могу даже снова проснуться Дэвидом Самптером. Типичные пользователи Instagram имеют 100–300 подписчиков, поэтому с учетом симметричных отношений (я подписан / на меня подписаны) есть вполне разумный шанс (примерно 1 / 200), что я проснусь собой. В любом случае крайне вероятно, что проведу несколько дней, путешествуя по своей социальной группе (мои френды, френды френдов и в целом люди, которые близки мне по культуре и происхождению).

Затем происходит то, что навсегда меняет мою жизнь. Я просыпаюсь Криштиану Роналду. Ну, не обязательно КриРо. Может, это будет Кайли Дженнер, Дуэйн «Скала» Джонсон или Ариана Гранде. Знаменитости могут быть разными, но само превращение в звезду гарантировано. Примерно через неделю после начала путешествия я стану одним из самых известных людей в Instagram. У этих знаменитостей сотни миллионов подписчиков, среди них есть люди из моей социальной группы, и вскоре я прыгну в их тела.

Я вполне могу оставаться в мире знаменитостей неделю или даже больше. Криштиану Роналду подписан на Дрейка, Новака Джоковича, Снуп Догга и Стефена Карри, так что мне предстоит перемещаться между спортивными звездами и рэперами. Из Дрейка я прыгаю в Фаррелла Уильямса, а затем в Майли Сайрус; она же ведет меня к Уиллоу Смит и Зендае. Теперь я свободно перемещаюсь по миру музыкантов и кинозвезд.

Затем после двух недель славы происходит еще одна трансформация – даже более драматичная, чем пробуждение в теле Снуп Догга. Однажды утром, проведя весь прошлый день на съемках боевика, я просыпаюсь школьным другом Дуэйна «Скалы» Джонсона. В этот момент осознаю ужасную истину. Я потерялся. Сейчас почти нет шансов, что я когда-нибудь снова стану Дэвидом Самптером. Совсем скоро я опять вернусь в круг знаменитостей, буду тусоваться со звездами и вывешивать фотографии своего полуобнаженного тела. Иногда эти периоды будут прерываться путешествиями по списку звезд рангом ниже, а изредка – кратковременным пребыванием в телах обычных людей; но после этого я снова вернусь в сияющий мир звездной жизни.

Вероятность того, что я стану собой завтра, становится крайне мала – возможно, один на триллион, а то и меньше. Все случайные путешествия по Instagram сходятся к знаменитостям и остаются там.

Одно важное уравнение XXI века выглядит так:

Забудьте о миллиардных заработках при использовании логистической регрессии в азартных играх. Это уравнение – основа индустрии с триллионами долларов. Это Google. Это Amazon. Это Facebook. Это Instagram. Это суть любого интернет-бизнеса. Оно создает суперзвезд и подавляет повседневное и обыденное. Оно создает авторитетов и возводит на престол королей и королев социальных сетей. Оно причина нашей непрерывной потребности во внимании, одержимости восприятием себя, разочарования и увлечения модой и побудительными мотивами знаменитостей. Из-за него мы ощущаем себя потерянными в море рекламы и продакт-плейсмента. Оно сформировало все аспекты нашей онлайн-жизни.

Это уравнение влияния.

Вы можете подумать, что такое важное уравнение очень трудно объяснить или понять. Это не так. Фактически я уже объяснил его, когда представил, как стал Криштиану Роналду, Дуэйном Джонсоном или Уиллоу Смит. Достаточно связать символы A (обозначает переходную матрицу) и p_t (вектор, определяющий вероятность оказаться тем или иным человеком в какой-то социальной группе в момент времени t) с тем путешествием, которое мы только что совершили по населению всего мира.

Чтобы наглядно представить переходную матрицу, вообразите себе электронную таблицу, в которой и строки, и столбцы подписаны именами людей. На пересечении стоит вероятность проснуться завтра другим человеком. Вообразите, что в мире живет всего пять человек: я, Дуэйн «Скала» Джонсон, певица Селена Гомес и еще двое, о ком я никогда не слышал: назову их Ван Фан и Ли Вэй. Если я предположу (как в своем первом мысленном эксперименте), что каждое утро просыпаюсь случайным человеком, то матрица A будет выглядеть так:

Столбцы и строки матрицы помечены инициалами пяти обитателей мира. Каждый день я смотрю на столбец того, кем сегодня оказался, а затем число в каждой строке сообщает мне вероятность того, что завтра я стану тем, с кем связана эта строка. Поскольку все числа равны 1/5, то это означает, что завтра я с равной вероятностью стану одним из пяти людей (включая меня самого).

Если я предположу (как во втором мысленном эксперименте), что буду просыпаться в теле того человека, на кого подписан в Instagram, то матрица A будет выглядеть иначе. Чтобы было интереснее, пусть Скала застрял на какой-то математической задачке и решил подписаться на меня в Instagram. Предположим, Селена Гомес познакомилась с Ван Фан и Ли Вэем на одном из своих концертов, подумав, что они здорово смотрятся вместе (я забыл упомянуть, что они пара), и подписалась на них. Разумеется, все подписаны на Селену и на Дуэйна. Тогда мы имеем:

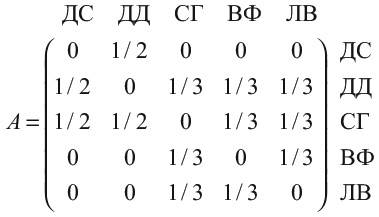
Когда я Дэвид Самптер, для меня есть только два возможных варианта на завтрашний день: Селена или Скала. Поэтому в каждой из соответствующих клеток в моем столбце стоит 1/2. То же верно и для Скалы Джонсона. Остальные жители планеты могут перейти в трех других людей. Нули по диагонали матрицы отражают тот факт, что мы не можем остаться собой второй день подряд, потому что не подписаны на себя.

Теперь обратите внимание, что для создания моей модели я использовал марковское свойство (): предположил, что то, кем я был два дня назад, никак не влияет на то, кем оказался сегодня. По сути, матрица A определяет цепь Маркова: она дает нам переходные вероятности для перемещения из одного состояния в другое, при этом следующее состояние зависит только от нынешнего, но не более ранних.

Будем постепенно двигаться по дням с помощью нашей матрицы A. Предположим, в первое утро я проснулся Дэвидом Самптером. Теперь вычислим вероятности того, кем я стану завтра.

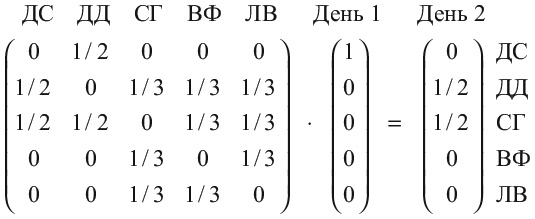
Я объясню, как умножаются матрицы, в примечаниях, но важнее всего обратить внимание на два столбца чисел в скобках по обеим сторонам от знака равенства. Они называются векторами, и каждый элемент вектора – число от 0 до 1, которое определяет вероятность того, что я окажусь определенным человеком в определенный день. В день 1 я Дэвид Самптер, так что число в моей строке равно 1, а остальные элементы вектора – 0. В день 2 я могу оказаться либо Селеной Гомес, либо Дуэйном Джонсоном (поскольку Дэвид Самптер подписан только на них), и в этом векторе есть два числа 1/2 для них, а остальные равны 0.

В день 3 все становится интереснее. Мы имеем:

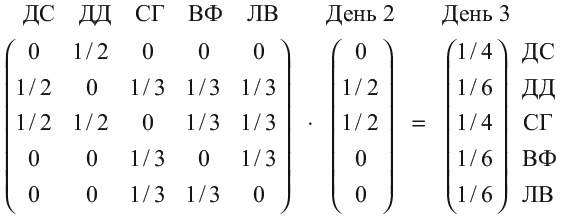
Я могу оказаться кем угодно из пяти человек. Скорее всего, я буду Дэвидом Самптером или Селеной Гомес, но с вероятностью 1/6 могу оказаться также и Джонсоном, и одним из китайских френдов Селены. Давайте произведем умножение еще раз, чтобы найти, кем я могу оказаться в день 4.

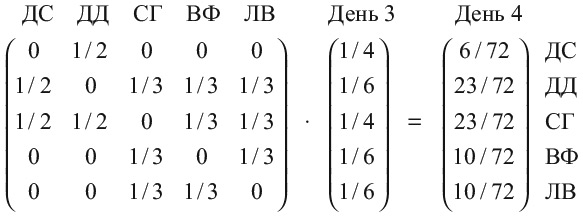
Теперь мы видим, как знаменитости выходят на центральные роли. Глядя на вектор вероятностей, вычисленный для дня 4, мы обнаруживаем, что вероятность оказаться Скалой или Селеной Гомес – 23/72 – почти вчетверо выше, чем вероятность оказаться Дэвидом Самптером (всего 6/72).

Каждый раз, умножая нашу матрицу с переходными вероятностями на вектор очередного дня, мы переходим на один день в будущее. А теперь вопрос, который стал движущей силой для всех моих путешествий по населению мира: насколько часто я буду одним из этих пяти людей через очень большой промежуток времени?

Именно на этот вопрос и отвечает уравнение 5. Чтобы увидеть как, заменим матрицу и векторы символами. Матрицу мы уже назвали A, а вектор назовем p_t и p_t+1. Тогда наше умножение матриц примет сжатую форму:

где p_t – вектор, определяющий вероятность быть тем или иным человеком в нашей социальной группе в момент t. Мы станем использовать индекс t, чтобы обозначать время, как в предыдущей главе. Мы уже видели, что

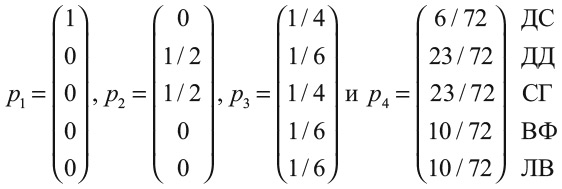
Переходим к уравнению 5, которое я повторю здесь:

Мы считаем, что прошло бесконечно много времени, поэтому разницы между t и t + 1 нет. Можем заменить эти индексы значком бесконечности ∞. Задумайтесь об этом. Отсюда следует, что если мы прыгали между телами достаточно много дней, то не имеет значения, прыгнем ли мы еще один раз: вероятность оказаться в некотором теле будет постоянной и определяться вектором p_∞. Назовем его стационарным распределением. Оно дает нам неизменное распределение вероятностей нахождения в том или ином состоянии (в теле того или иного человека) через очень большое время, когда то, кем мы были изначально, уже забылось.

Уравнение 5 определяет вероятность того, что я буду определенным человеком в какой-то день в отдаленном будущем. Осталось решить уравнение. Для вселенной из пяти человек, в которой я сейчас обитаю, мы находим, что:

Обратите внимание, что два вектора слева и справа от знака равенства одинаковы. Это значит, что, сколько бы раз я ни умножал на этот вектор переходную матрицу A, результат не изменится. Именно таковы в отдаленной перспективе мои вероятности оказаться тем или иным человеком.

Вывод? У меня вдвое больше шансов проснуться Дуэйном Джонсоном, чем Дэвидом Самптером, и еще больше – Селеной Гомес. Больше даже шансов стать Ван Фан и Ли Вэем, чем Дэвидом. Если перевернуть вероятности, можно узнать, сколько времени мы проведем в телах всех жителей нашего мира. Шестьдесят дней – примерно два месяца, и стационарное распределение говорит нам, что в среднем 8 дней из них я буду Дэвидом, 16 – Джонсоном, 18 – Гомес, по 9 – Ван Фан и Ли Вэем. Когда время сдвигается к бесконечности, более половины жизни я проведу как знаменитость.

Ясно, что мы не просыпаемся каждое утро разными людьми, но Instagram дает нам возможность заглянуть в чужую жизнь. Каждая увиденная фотография – момент, когда подписчик несколько секунд ощущает, каково быть кем-то еще.

Twitter, Facebook и Snapchat тоже дают возможность распространять информацию и влиять на чувства и мысли подписчиков. Стационарное распределение p_∞ измеряет такое влияние; и не только с точки зрения того, кто на кого подписан, но и с точки зрения скорости, с которой тот или иной мем или идея распространяется среди пользователей. Люди с большими вероятностями в векторе p_∞ влиятельнее и распространяют мемы быстрее. Люди с маленькими вероятностями в векторе p_∞ менее влиятельны.

Вот почему уравнение 5 – уравнение влияния – так ценно для сетевых гигантов. Оно говорит им, кто в их соцсети самые важные люди, и при этом компании ничего не знают о том, кто они в реальности и чем занимаются. Измерение влиятельности – всего лишь вопрос матричной алгебры, и этим бездумно и некритично занимается компьютер.

Изначально уравнение влияния применила Google при разработке своего алгоритма ранжирования страниц PageRank – незадолго до рубежа веков. Компания вычисляла стационарные распределения для сайтов в предположении, что пользователи случайным образом щелкают по ссылкам на посещенных сайтах, чтобы выбрать следующий, на который перейдут. По этой причине в результатах поиска они выше ставили сайты с более высокими значениями p_∞. Примерно в то же время Amazon стала создавать матрицу смежности A для своего бизнеса. В ней связывались те книги, а позже игрушки, фильмы, электроника и другие товары, которые люди покупали вместе. Определив тесные связи в матрице, компания смогла давать рекомендации для клиентов под заголовком вроде «Вам также может понравиться». Twitter использует стационарное распределение в своей соцсети, чтобы найти и предложить вам людей, на которых можно подписаться. Facebook применяет те же идеи при обмене новостями, а YouTube – чтобы рекомендовать видеоролики. Со временем подход развивался, появлялись дополнительные детали, но базовым инструментом для нахождения влиятельных лиц в соцсети остается матрица смежности A и ее стационарное распределение p_∞.

За последние два десятилетия это привело к неожиданному результату. Система, которая первоначально создавалась для измерения влияния, превратилась в его создателя. Алгоритмы на базе уравнения влияния определяют, какие публикации должны занимать видное место в социальных сетях. Идея в том, что если некто популярен, то этого человека желают выслушать больше людей. Результатом становится цикл обратной связи: чем влиятельнее человек, тем большую заметность дает ему алгоритм, а от этого его влияние еще больше растет.

Один бывший сотрудник Instagram рассказал мне, что изначально основатели компании очень неохотно применяли в бизнесе алгоритмы и математику. «Они видели в Instagram нечто очень нишевое, артистичное и считали алгоритмы негодными», – говорил он. Эта платформа предназначалась для обмена фотографиями между близкими друзьями. Все изменилось после успеха Facebook. «За последние пару лет платформа стала совершенно иной. Один процент ее пользователей имеет более 90 % подписчиков», – заметил мой собеседник.

Вместо того чтобы побуждать пользователей подписываться только на друзей, компания применила к своей сети уравнение влияния. Оно еще сильнее раскручивало самые популярные аккаунты. Возникала обратная связь, и аккаунты знаменитостей росли всё сильнее. Едва Instagram стал использовать уравнение влияния, как и все платформы социальных сетей до него, его популярность резко возросла – в нем более миллиарда пользователей.

Математические методы, используемые при конструировании соцсетей, появились задолго до возможности создания таких приложений. Вовсе не Google изобрела уравнение влияния: его происхождение восходит к Маркову, который предложил свойство, получившее его имя, для рассмотрения цепей состояний, где каждое новое состояние зависит только от предыдущего. Именно это и происходит при моем случайном путешествии по Instagram.

Решая уравнение 5 для моего мира из пяти человек, я слегка поленился. Я нашел ответ – вероятность, с которой буду тем или иным человеком в отдаленном будущем, – многократно перемножая матрицу A и вектор p_t, пока тот не перестал меняться. Сделав это, я нашел p_∞.

Такой метод в итоге приводит к правильному ответу, но он не особо изящен. И Google им не пользуется. Свыше ста лет назад математики Оскар Перрон и Георг Фробениус показали, что для любой цепи Маркова с матрицей A существует единственное стационарное распределение p_∞. Итак, независимо от структуры социальной группы мы всегда можем вычислить, сколько времени будем проводить тем или иным человеком, если станем случайным образом перемещаться между людьми. Это стационарное распределение можно найти с помощью метода Гаусса, который, как и нормальная функция, связан с именем Карла Фридриха Гаусса, однако восходит к более древним временам: китайские математики решали системы линейных уравнений с помощью этого метода больше двух тысяч лет назад. К матрице A применяются так называемые элементарные преобразования, чтобы привести ее к более удобному виду и найти в итоге p_∞. Это дает возможность быстро и эффективно находить влиятельных людей даже для сетей с миллионами участников.

На протяжении XX века «Десятка» изучала свойства сетей; соответствующая область математики называется теорией графов. Еще в 1922 году Джордж Удни Юл описал математику, стоящую за ростом популярности в Instagram, в терминах процесса, который позже был назван «предпочтительным присоединением»: чем больше у человека подписчиков, тем больше он привлекает к себе внимания, и его известность растет. Затем, в начале XXI века, всего за несколько лет до появления Facebook, эта область исследований расширилась и стала именоваться наукой о сетях: сейчас она описывает распространение мемов и фейковых новостей, изучает, как соцсети создают маленький мир, в котором все соединены через шесть рукопожатий, и потенциальную возможность поляризации.

«Десятка» была готова. Ее участники оказались среди основателей и первых работников будущих гигантских соцсетей. В основе их бизнеса лежит уравнение влияния. Зарплата, предложенная людям с нужными умениями, была достаточно соблазнительной даже для самых идеалистичных участников общества. И что еще важнее, эта работа давала им свободу для творческого мышления, создания новых моделей и их практического применения.

Вскоре перед участниками «Десятки» поставили задачу установить, как мы реагируем на соцсети. Они управляли лентой новостей Facebook, чтобы посмотреть, как пользователи реагируют, получая только негативные новости; они создавали кампании в сетях, чтобы побудить людей голосовать на выборах; конструировали фильтры, чтобы пользователи читали больше тех новостей, которые им интересны. Они контролировали то, что мы видели, определяя, видим ли мы публикации друзей, новости (фейковые и реальные), знаменитостей или рекламу. Именно участники «Десятки» стали влиятельными – не из-за сказанного ими, а благодаря их решениям о том, как нам связываться друг с другом. Они знали о нас даже то, чего мы не знали сами…

Вероятно, ваши друзья намного популярнее вас. Я ничего не хочу сказать о вас как о человеке, не желаю быть к вам несправедливым, но могу утверждать это с определенной уверенностью.

Математическая теорема, известная как парадокс дружбы, утверждает, что большинство людей в любой социальной сети, включая Facebook, Twitter и Instagram, менее популярны, чем их друзья. Начнем с примера. Представьте, что мы убрали Дуэйна Джонсона из той социальной сети, которую описывали ранее. Теперь нас четверо – я, Селена Гомес, Ван Фан и Ли Вэй, и они имеют, соответственно, 0, 3, 2 и 2 подписчика. Вероятно, китайская пара чувствует себя довольно популярной за счет компании Гомес, но у меня есть для нее сюрприз. Я прошу каждого участника сети посчитать среднее число подписчиков у их друзей. Я подписан только на Селену Гомес, у нее три подписчика, поэтому среднее число подписчиков у моих друзей равно 3. Гомес подписана на двух людей, у каждого по 2 подписчика, так что среднее число подписчиков у ее друзей равно 2. Ван Фан и Ли Вэй подписаны друг на друга и на Гомес, поэтому их друзья в среднем имеют 2,5 подписчика. Таким образом, среднее число подписчиков у друзей в этой сети равно (3 + 2 + 2,5 + 2,5) / 4 = 2,5. Только Селена Гомес имеет больше друзей, чем ее подписчики. У Ван Фан, Ли Вэя и у меня число подписчиков ниже среднего.

Причина парадокса дружбы заключается в разнице между случайным выбором человека и случайным выбором отношения дружбы (см. рис. 5). Для начала выберем наугад одного человека. Ожидаемое (среднее) количество подписчиков у него – сумма числа подписчиков у всех пользователей, поделенная на общее число пользователей платформы. Для Facebook это число составляет около 200. Для нашей сети из четырех человек это (0 + 3 + 2 + 2) / 4 = 1,75. В теории графов это называется средним числом ребер, входящих в узел. Выше мы показали, что среднее число подписчиков у друзей в этой сети равно 2,5, что больше, чем 1,75 – среднее число подписчиков.

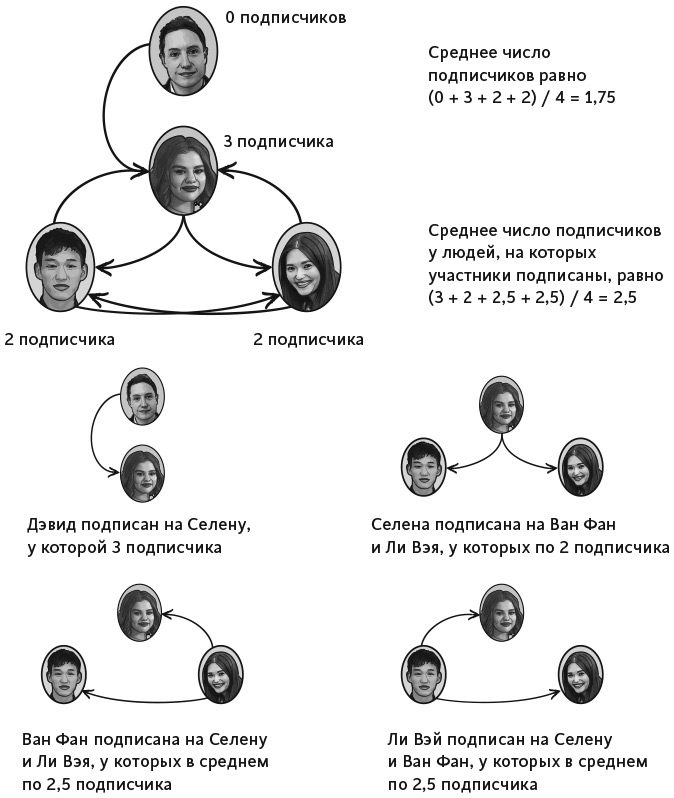
Рис. 5. Парадокс дружбы для четырех участников

То же произойдет, если мы снова вернем в нашу сеть Дуэйна Джонсона. Результат сохранится, даже если Селена Гомес подпишется на меня. Парадокс дружбы можно доказать для любой соцсети, в которой каждый подписан на одно и то же количество людей. Доказательство таково. Сначала выберите наугад одного человека во всей сети; затем – кого-нибудь, на кого этот человек подписан. Если представить ситуацию иначе, то мы, выбрав двух связанных людей, взяли какую-то случайную связь среди всех изображающих отношения «подписанности» людей в соцсетях. В теории графов такие связи называются ребрами графа. Теперь, поскольку популярные люди имеют (по определению) больше входящих ребер, на конце любого данного ребра мы с большей вероятностью найдем популярного человека, чем если бы выбирали человека наугад. Таким образом, случайно выбранный друг случайно выбранного человека (человек на конце ребра), вероятно, имеет больше друзей, чем случайно выбранный человек. Это и показывает, что парадокс дружбы справедлив.

Такова математическая теория. Как все это работает на практике? Кристина Лерман, исследователь из Университета Южной Калифорнии, решила выяснить это. Она и ее коллеги взяли социальную сеть пользователей Twitter в 2009 году (на такой ранней стадии развития соцсети в ней было всего 5,8 миллиона пользователей) и рассмотрели отношения «подписанности». Ученые обнаружили, что люди, на которых был подписан типичный пользователь Twitter, имели примерно вдесятеро больше подписчиков, чем он. Только 2 % пользователей были популярнее своих подписчиков.

Лерман и ее коллеги пришли еще к одному выводу, который полностью противоречит интуиции. Оказалось, что подписчики случайно выбранного пользователя Twitter были в среднем в двадцать раз лучше связаны! Хотя кажется разумным, что люди, на которых мы подписаны, популярны (в конце концов, многие из них – знаменитости), гораздо труднее понять, почему люди, подписанные на нас, оказываются намного популярнее нас. Если они подписаны на вас, как они могут быть популярнее? Это не выглядит справедливо.

Ответ – в нашей склонности создавать взаимные отношения. Когда кто-то подписывается на вас, появляется определенное социальное давление, заставляющее сделать то же в ответ. Отказ выглядит грубостью. В среднем люди, подписанные на вас в Instagram или отправившие вам запрос в друзья в Facebook, также с большой вероятностью отправят аналогичные запросы другим людям. В результате они составят большую часть нашей социальной группы. И это еще не всё. Исследователи также обнаружили, что ваши друзья выкладывают посты чаще, получают больше лайков, репостов и охватывают больше людей, чем вы.

Как только вы примете математическую неизбежность непопулярности, ваши отношения с соцсетями начнут улучшаться. Вы не одиноки. По оценке Кристины Лерман и ее коллег, 99 % пользователей Twitter в том же положении. В самом деле, у популярных людей положение может оказаться еще хуже. Подумайте об этом. В нескончаемом поиске лучшего социального положения «крутые ребята» пытаются добиться взаимных отношений с теми, кто успешнее их. Чем чаще они это делают, тем скорее оказываются в окружении людей, которые популярнее, чем они сами. Это слабое утешение, но приятно осознавать, что те, кто кажется успешным, вероятно, ощущают то же, что и вы. Возможно, за исключением Пирса Моргана и Джоан Роулинг, оставшийся 1 % пользователей Twitter – либо аккаунты знаменитостей, которыми управляют пиар-службы, либо, весьма вероятно, люди, которые почти обезумели от стремления постоянно находиться в соцсетях.

Я не собираюсь присоединяться к тем, кто предлагает вам уйти из соцсетей. Мантра математика – не сдаваться. Нужно разделить все на три составные части: данные, модель и бессмыслицу.

Рекомендую начать сегодня. Прежде всего посмотрите на данные. Проверьте сами, сколько подписчиков или взаимных друзей имеют ваши друзья в Facebook или Instagram. Я только что сделал это для Facebook и обнаружил, что 64 % моих друзей популярнее меня. Затем вспомните модель. Популярность в соцсетях создается с помощью обратной связи, благодаря которой люди привлекают больше подписчиков. Это статистическая иллюзия, порожденная парадоксом дружбы. Затем убирайте бессмыслицу. Не жалейте себя и не ревнуйте к другим: просто осознайте, что мы часть Сети, которая искажает нашу самооценку самыми разными способами.

Психологи пишут и говорят о наших когнитивных искажениях, при которых отдельные люди или общество в целом воспринимают субъективную реальность, не совпадающую с реальным миром. Список таких искажений растет: «горячая рука», эффект присоединения к большинству, ошибка выжившего, предвзятость подтверждения, эффект фрейминга. Участники «Десятки», разумеется, не отрицают существования таких искажений, но для них важнее не ограничения человеческой психологии. Вопрос в том, как убрать фильтр и увидеть мир четче. Для этого они придумывают сценарии «Что, если?». Что, если я буду просыпаться каждый день другим человеком? Что, если я путешествую по Snapchat как интернет-мем? Что, если буду читать только те новости, которые мне предлагает Facebook, и смотреть только фильмы, рекомендованные Netflix? Как тогда будет выглядеть для меня мир? И как это отличается от «более справедливого» мира, в котором я уделяю равное внимание всей доступной мне информации?

«Десятка» предлагает вам представить себе невероятные, фантастические сценарии. Затем они становятся математическими моделями. После этого можно начинать цикл. Модель сравнивается с данными, а те используются для совершенствования модели. Медленно, но верно участники «Десятки» могут убрать фильтр и раскрыть нашу социальную реальность.

Лина и Микаэла открывают свои аккаунты в Instagram и показывают мне свои телефоны. «Это реклама или селфи?» – спрашиваю я Лину.

Лина показывает фотографию местного пекаря, который демонстрирует на камеру поднос, полный пирожных в виде сердечек. Фотография выглядит настоящей, но идея здесь в приглашении подписчиков в магазин. Лина отвечает, что это селфи, но она классифицирует аккаунт как компанию.

Лина и Микаэла работают над своей дипломной работой по математике. Они изучают, как Instagram представляет им мир. Незадолго до того, как они начали свой проект, Instagram снова обновил алгоритм, который определяет порядок показа фотографий. Компания заявила, что акценты сместились в сторону приоритетов снимков от друзей и семьи.

В результате многие популярные люди ощутили угрозу. Шведская блогерша и гуру соцсетей Анита Клеменс (65 тысяч подписчиков) сказала: «Психологически трудно видеть, как мои подписчики исчезают. Мне почти сорок, интересно, каково это для всех молодых авторитетов?»

Клеменс ощущала, что она активно работала «для своих подписчиков», а новый алгоритм не доносил до них ее сообщения. Чтобы проверить ограничения, она опубликовала свою фотографию с новым партнером: легко было ошибочно решить, что на снимке она беременна.

Эта фотография широко разошлась по платформе, а затем Клеменс раскрыла, что ее основной целью была проверка того, какие снимки срабатывают, а какие нет. Заявление о своей беременности в Instagram, похоже, работает, если вы желаете привлечь больше внимания.

Хотя реакция на один снимок с ложной беременностью дает очень мало информации, можно сказать, что Клеменс проводит своего рода эксперимент. Келли Коттер из Университета штата Мичиган обнаружила, что многие популярные люди в Instagram пытаются понять алгоритм и манипулировать им. Они открыто обсуждают расходы и выгоды от лайков и комментирования максимально возможного количества постов, проводя A/B тестирование для разных стратегий (вспомните уравнение ставок). Часто такие люди пытаются определить, не «затеняет» ли их сайт, опуская их посты ниже в ленте подписчиков. Когда Instagram изменил свои алгоритмы, многие из этих людей поспешили написать в социальных сетях заявления с хештегом .

Теперь Лина и Микаэла планировали тщательнее изучить алгоритм Instagram исходя из собственной позиции типичных пользователей. В течение месяца они будут открывать свои аккаунты только один раз в день в 10 утра, смотреть на порядок показываемых фотографий и отмечать тип каждого поста и сообщения. Так они могут проверить гипотезу популярных лиц, что алгоритм затеняет их и снижает их приоритет.

«Я думаю, что более редкое появление в аккаунте пойдет нам на пользу», – говорит Микаэла, имея в виду то, что они собирают данные всего один раз в день. Как и многие из нас, эти молодые женщины проверяют свои соцсети чаще, чем на самом деле хотят.

Задача в том, чтобы провести обратную разработку (реверс-инжиниринг) алгоритма, который использует Instagram: выяснить, что сеть от них скрывает (если она это делает). В математике это называется обратной задачей, и один из примеров использования – современная компьютерная томография. Когда пациент лежит в аппарате, во всех направлениях производятся снимки с помощью рентгеновских лучей. Материалы разной плотности в нашем теле поглощают рентгеновские лучи по-разному, что позволяет видеть скелет, легкие, мозг и другие системы нашего тела. Обратная задача в этом случае – собрать все снимки воедино, чтобы получить полное изображение наших внутренних органов. Математический метод, лежащий в основе этого процесса, – преобразование Радона (названное в честь предложившего его австрийского математика Иоганна Радона), которое дает возможность восстановить точную трехмерную картину по отдельным двумерным изображениям.

У нас нет преобразования Радона для социальных сетей, но имеется – в форме уравнения 5 – ясное понимание того, как они поглощают и изменяют социальную информацию. Чтобы провести обратную разработку процесса деформации данных, который применяет Instagram, Лина и Микаэла использовали статистический метод под названием бутстрэппинг. Каждый день они брали первые 100 сообщений в своей ленте и случайным образом перемешивали их, создавая новый порядок. Они повторяли этот процесс 10 000 раз, получая распределение перестановок, которое имело бы место, если бы Instagram просто показывал посты случайно, не устанавливая для них какие-то приоритеты. Сравнивая положение популярных людей в реальной ленте Instagram с таким рандомизированным ранжированием, они смогли определить, сдвигаются ли такие люди в их ленте вверх или вниз.

Результаты резко противоречили мнениям, вызвавшим появление хештега . Не нашлось подтверждений тому, что каких-то популярных людей угнетали: их положение в лентах Лины и Микаэлы статистически не отличалось от того, каким оно было бы при случайном порядке. Оказалось, что Instagram нейтрально относится к таким лицам. Однако некоторые аккаунты получили существенный приоритет: друзья и семья поднимались на верх ленты. Это происходило в основном за счет новостных сайтов, политиков, журналистов и организаций. Instagram не столько снижал влияние популярных людей в ленте, сколько увеличивал влияние друзей и семьи и затенял аккаунты, которые не платили за рекламу.

Самым показательным в кампании было ощущение незащищенности популярных людей. Они внезапно осознали, что у них не так много контроля над социальным положением, как они думали. Их позиции определялись алгоритмом, который способствовал популярности, а теперь они беспокоились, что ее отнимет другой алгоритм, ориентированный на друзей.

Это исследование показало, что настоящие влиятельные лица в сети не те, кто публикует снимки своей еды и моментов жизни. Скорее, это программисты Google, Facebook и Instagram, конструирующие фильтры, через которые мы смотрим на мир. Они решают, кто популярен и что популярно.

Для Лины и Микаэлы эксперимент оказался терапевтическим. Лина сказала мне, что изменился ее взгляд на Instagram. Она ощутила, что теперь лучше использует свое время в этом приложении. «Вместо того чтобы прокручивать ленту в поисках интересного, я останавливаюсь, увидев посты друзей. Я знаю, что дальше будет просто скукота», – говорит она.

Уравнение влияния справедливо не для одной социальной сети; оно относится ко всем. Его сила – способность показать, как структура онлайн-сетей формирует ваш взгляд на мир. Когда вы ищете товары на Amazon, то попадаете в систему «вам также может понравиться», поскольку самые популярные продукты показываются первыми. Twitter сочетает полярные мнения с возможностью оспаривания ваших взглядов людьми со всего мира. В Instagram вас окружают друзья и семья, вы ограждены от новостей и мнений. Используйте уравнение 5, чтобы честно рассмотреть, кто и что на вас влияет. Напишите матрицу смежности для вашей социальной сети и посмотрите, кто находится в вашем онлайн-мире, а кто вне его. Подумайте о том, как эта соцсеть влияет на вашу самооценку и как контролирует информацию, к которой вы имеете доступ. Подвигайтесь в ней и посмотрите, как это затрагивает других людей, с которыми вы связаны.

Через несколько лет Лина и Микаэла, которые планируют стать преподавателями математики, будут объяснять подросткам, как алгоритмы телефонов фильтруют взгляды на мир. Большинству детей этот урок поможет разобраться в сложной социальной группе, в которую они встроены. А некоторые увидят другую возможность – карьерную. Они станут серьезно учиться, глубже понимать математику и узнавать, как применять алгоритмы, используемые Google, Instagram и прочими компаниями. Некоторые из них могут пойти дальше и стать частью богатой и влиятельной элиты, которая контролирует, как нам подается информация.

В 2001 году сооснователь Google Ларри Пейдж получил патент на использование уравнения 5 при поиске в интернете. Изначально тот принадлежал Стэнфордскому университету, в котором тогда работал Пейдж, и Google приобрел его за 1,8 миллиона акций компании. В 2005 году Стэнфорд продал эти акции за 336 миллионов долларов. Сегодня они стоили бы в десять раз больше. Применение уравнения 5 – это лишь один из многих патентов Google или Facebook, где к интернету применяют математику XXI века. Теория графов стоит миллиарды для технических гигантов, ее применяющих.

Тот факт, что математические формулы, созданные почти за сто лет до подачи патента, могут принадлежать какому-нибудь университету или компании, похоже, противоречит духу «Десятки». У участников всегда были секреты, однако ими обычно делились, их использовали все желающие. Должны ли у общества быть принципы, которые не позволяют его участникам ограждать свои открытия или получать сверхприбыль от своих тщательно собранных знаний?

Оказывается, ответ на этот вопрос далеко не очевиден…