Книга: Десять уравнений, которые правят миром. И как их можете использовать вы
Назад: Глава 2. Уравнение суждений
Дальше: Глава 4. Уравнение умений
Глава 3. Уравнение уверенности
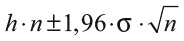
Не вся «Десятка» родилась из христианской морали. Если бы нас попросили отправиться в ту точку пространства и времени, где ей было положено начало, то это оказалось бы не смертное ложе Томаса Байеса. Мы очутились бы в Лондоне, но почти на тридцать лет раньше – на собрании друзей 12 ноября 1733 года, где слушали бы, как Абрахам де Муавр раскрывает секреты азартных игр.
Де Муавр был «нестандартным» математиком. Его изгнали из Франции как протестанта, а в Лондоне к нему относились с подозрением из-за его национальности. Его современники – Исаак Ньютон и Даниил Бернулли – стали профессорами в своих областях, а де Муавру приходилось зарабатывать другими способами. Он давал частные уроки для детей среднего класса в Лондоне (предполагается, хотя это и не доказано, что одним из его учеников был юный Томас Байес), занимался «консультациями». Его можно было найти в кофейне Old Slaughter’s на Сент-Мартинс-Лейн, где он давал советы всем – от игроков и финансистов до самого сэра Исаака Ньютона.
Работа де Муавра, появившаяся в 1733 году, была более изощренной по сравнению с его ранними трудами. Он показал, как новая математика – анализ, недавно разработанный Исааком Ньютоном, – помогает определить уровень уверенности в долгосрочной прибыльности в играх, опирающихся на случай. В итоге представленное им уравнение станет основой того, как специалисты в естественных и социальных науках определяют уровень доверия к их исследовательским результатам. Но чтобы понять, откуда взялось уравнение уверенности, нужно начать оттуда же, что и де Муавр. Нужно войти в сомнительный мир азартных игр.
* * *
Сегодня требуется всего несколько минут, чтобы открыть счет для ставок в онлайн-казино. Имя, адрес и (главное) данные карточки – и готово. Игры разные. Есть онлайн-покер, где вы играете против других, а казино получает свою долю. Есть игровые автоматы, похожие на те, что когда-то ставили в пабах; у них свои имена – например, Cleopatra’s Tomb, Fruit vs Candy и Age of the Gods, а также торговые марки вроде Batman v Superman и Top Trumps Football Stars. Вы нажимаете на кнопку, вращаете колесо и, если боги выстраиваются в ряд или в ряду достаточно Бэтменов, выигрываете. Наконец, есть традиционные для казино игры – например, блек-джек и рулетка, – которые транслируются в прямом эфире: элегантно одетые юноши раздают карты, а женщины в вечерних платьях с низким вырезом крутят колесо рулетки.
Я открыл счет на одном популярном сайте онлайн-игр. Положил 10 фунтов стерлингов и получил бонус в 10 фунтов за новый счет, что дало мне стартовый капитал в 20 фунтов. Я решил начать с «Века богов» – только по той причине, что там разрешались самые маленькие ставки. Соответственно, при цене 10 пенсов за вращение у меня было больше попыток.
Через двенадцать попыток у меня оказалось на 70 пенсов меньше и не было ощущения, что что-то происходит. Боги мне наскучили, и я отправился на Top Trumps крутить Криштиану Роналду, Месси и Неймара. Это было дороже, по 20 пенсов за вращение, но через шесть попыток я выиграл (1,5 фунта!) и почти вернулся к своему начальному капиталу. Я попробовал «Бэтмен против Супермена» и несколько других игр. Затем нашел кнопку автоматического запуска и теперь мог крутить постоянно без необходимости нажимать на кнопку. Впрочем, это была плохая идея. Спустя двести попыток у меня осталось 13 фунтов.
Мне показалось, что игровые автоматы не оптимальны по соотношению цены и качества, и я решил попробовать живое казино. За столом распоряжалась Керри, женщина двадцати с небольшим в черном платье. Она приветствовала меня и заговорила с другим клиентом. Это был странный опыт. Я мог набирать сообщения, а она отвечала.
– Как погода у вас? – спросил я.
– Хорошая, – ответила она, посмотрев прямо на меня. – Кажется, весна на подходе. Сейчас последние ставки. Удачи!
Она жила в Латвии и уже четыре раза бывала в Швеции. Немного поболтав, я спросил ее, были ли сегодня крупные выигрыши.
– Мы не видим, сколько вы ставите, – сообщила она.
Я чувствовал себя несколько глупо; старался ставить 1 фунт при каждом вращении колеса, так что она не думала, будто я дешевка.
Керри мне нравилась, но я ощущал, что мне нужно лучше осмотреться. Не знаю, как это выразить, но была какая-то причина, по которой она и большинство ее коллег-мужчин работали в зале с низкими ставками. Керри было слегка неловко и некомфортно в обтягивающем платье, и она не казалась сексуальной.
Залы с более высокими ставками выглядели иначе. Вырез на платьях был глубже, а улыбки завлекательнее. Перед каждым вращением Люси, работавшая в помещении, где я находился, осознанно смотрела в камеру, словно говоря, что мой выбор верный. Мне пришлось заставить себя вспомнить, что она смотрела не только на меня, но и на 163 других игроков со всего мира.
Люси отвечала на вопросы клиентов.
– Да, у меня есть партнер. Но все сложно, – говорила она одному.
– О, я люблю путешествовать, – сообщала другому. – Я бы с радостью поехала в Париж, Мадрид, Лондон…
Камера переключилась на вид сверху, давая возможность увидеть ее ноги перед тем, как колесо пришло во вращение.
Мне стало очень некомфортно. Приходилось напоминать себе, зачем я здесь в первую очередь. Вернулся в помещение с более низкими ставками – там работал Макс, вежливый молодой человек, который давал статистические советы по выигрышным цветам и номерам. Похоже, на его рулетке хорошо шли большие числа.
Посмотрел на свой баланс. Я наугад ставил на красное и черное, особо не раздумывая, и с удивлением увидел, что после нескольких часов в казино у меня имелось 28 фунтов. Прибыль 8 фунтов за вечер. Дела шли хорошо.
* * *
Как узнать, почему мы выигрываем: потому что умело играем или потому что нам повезло? Я знал, что в онлайн-казино шансы против меня, пусть даже я после двух-трех часов и пополнил немного свой счет.
В других играх я не знаю, есть у меня преимущество или нет. Если я играю в покер с друзьями, то вижу, как моя стопка фишек растет и уменьшается. Но сколько времени пройдет, прежде чем я смогу сказать: я – лучший игрок? Если я установил стратегию спортивных ставок, как для чемпионата мира, – когда я узнаю, что она окупается?
Такие вопросы не ограничиваются азартными играми и спортом; они могут быть и политическими. Сколько избирателей нужно опросить, чтобы надежно оценить, кто выиграет президентские выборы в США? Они могут быть связаны с обществом: как узнать, проявляет ли компания расовую дискриминацию при найме людей? И даже личными: сколько времени вы должны отдать работе или отношениям с другим человеком, прежде чем решиться что-то поменять?
Удивительно, но существует формула, которая отвечает на все эти вопросы: назовем ее уравнением уверенности. Вот оно:

Понятие степени уверенности отражается центральным символом ± (плюс-минус). Представьте, что вы спрашиваете меня, сколько чашек кофе в день я выпиваю. Я не знаю наверняка, поэтому могу сказать что-то вроде «четыре плюс-минус парочка», или 4 ± 2. Это – доверительный интервал, удобное обозначение и среднего значения, и отклонения от него. Это не значит, что я никогда не могу выпить 7 чашек (или только одну), но я вполне уверен, что в большинстве случаев выпиваю от 2 до 6 чашек.
Уравнение 3 позволяет нам делать более точные утверждения о нашей уверенности в каком-либо событии. Представьте, что я прошу всех читателей этой книги запустить 400 раз колесо рулетки, ставя по 1 фунту на красное или черное. На рулетке 37 номеров: от 1 до 36, раскрашенные поочередно в красный и черный цвета, и особый зеленый 0 (зеро). Он обеспечивает преимущество казино. Например, если какой-то игрок ставит на красное, то вероятность попадания шарика на красный номер составляет 18/37, и в случае этого события игрок возвращает свою ставку и получает еще такую же сумму. Вероятность потери денег (непопадания шарика на красный цвет) составляет 1 – 18/37 = 19/37. Ожидаемый (средний) выигрыш игрока при ставке в 1 фунт составляет 1 ∙ 18/37 – 1 ∙ 19/37 = –1/37; поэтому при каждом повороте колеса игрок в среднем проигрывает 2,7 пенса. В уравнении 3 средний проигрыш обозначен буквой h, и в нашем случае h = –0,027 (фунтов). За 400 попыток каждый из читателей проиграет в среднем h ∙ n = 0,027 ∙ 400 = 10,8 фунта.
Следующий шаг – определить степень отклонения от среднего. Не каждый читатель проиграет (или выиграет) одну и ту же сумму. Даже без арифметических подсчетов понятно, что при одном обороте рулетки можно наблюдать большую разницу в результатах: если я ставлю 1 фунт, то либо удвою свои деньги, либо потеряю их. Отклонение имеет такую же величину, как инвестируемая сумма, и гораздо больше, чем средняя потеря в 2,7 пенса.
Определим отклонение количественно. Для этого найдем средний квадрат разности между результатом одного вращения и средним значением. Среднее значение равно –0,027 фунта, и если мы выиграли фунт, то квадрат разности равен (1 – (–0,027))2 = 1,0547, а если проиграли 1 фунт, то (–1 – (–0,027))2 = 0,9467. Всего есть 18 удачных исходов и 19 неудачных, поэтому средний квадрат разности, который обозначают σ2, равен:
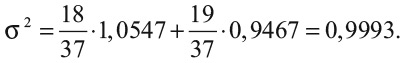
Такой средний квадрат разности σ2 называют дисперсией. У рулетки она очень близка к единице, но не равна ей. Если бы на рулетке было только 36 номеров, половина красных и половина черных, дисперсия была бы в точности единица.
Дисперсия увеличивается пропорционально количеству вращений колеса. Если я запускаю колесо рулетки дважды, она удваивается; если три раза – утраивается и т. д. Дисперсия при n попытках равна n ∙ σ2.
Обратите внимание, что при вычислении дисперсии мы возводим разность в квадрат, поэтому ее размерность – фунты в квадрате, а не фунты. Чтобы получить снова фунты, можно извлечь из дисперсии квадратный корень и получить так называемое среднеквадратичное (стандартное) отклонение σ; в нашем случае σ = 0,9996. Соответственно, за 400 оборотов мы получим среднеквадратичное отклонение
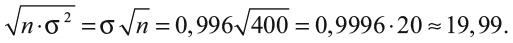
Теперь у нас есть большая часть компонентов для уравнения уверенности. Единственный элемент, который мы еще не объяснили, – число 1,96. Оно появляется из математической формулы, которая описывает кривую нормального (гауссовского) распределения; эта колоколообразная кривая используется для представления роста людей или их IQ. Вы можете вообразить нормальное распределение в виде колокола с точкой максимума в среднем значении (например, при запуске рулетки 400 раз средний выигрыш будет 10,8 фунта; если мы станем измерять рост мужчин в Великобритании, то среднее значение будет 175 сантиметров). На рисунке 3 показана кривая нормального распределения для 400 запусков рулетки и ставок по 1 фунту.
Теперь представьте, что мы хотим найти интервал, который содержит 95 % площади этой колоколообразной фигуры.
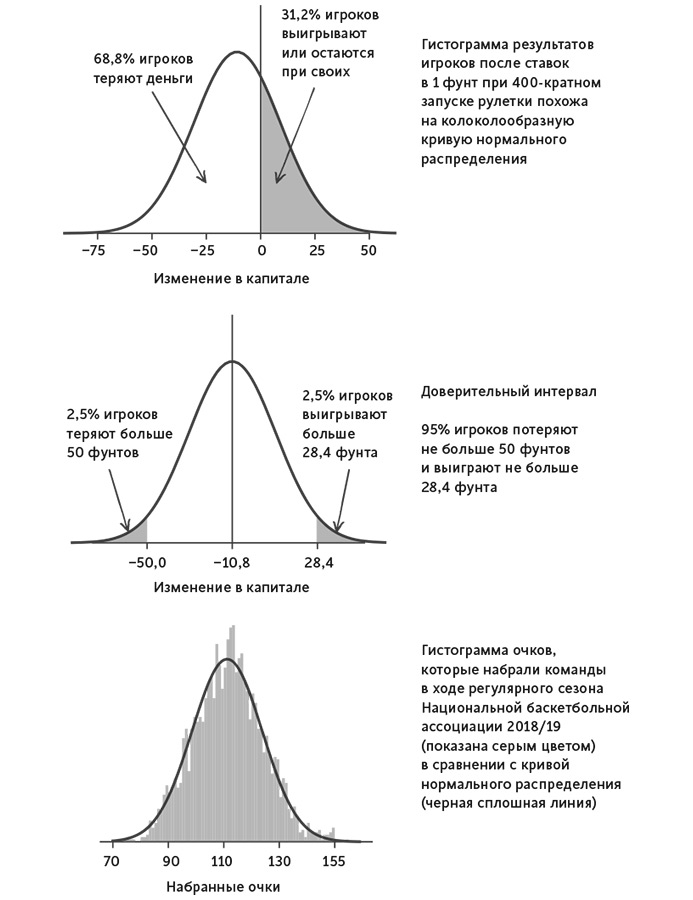
Рис. 3. Нормальное распределение
Для 400 запусков рулетки это интервал, куда попадут 95 % прибылей или убытков читателей. Величина 1,96 берется именно отсюда. Чтобы интервал содержал 95 % наблюдений, его граничные значения должны в 1,96 раза превосходить среднеквадратичное отклонение. Иными словами, в нашем случае 95 %-й доверительный интервал для нашей прибыли после 400 запусков рулетки определяется уравнением 3:
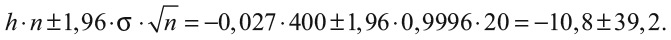
После 400 запусков рулетки читатель в среднем потеряет 10,8 фунта. Печально. С другой стороны, ±39,2 определяет довольно широкий доверительный интервал, поэтому некоторые читатели преуспеют. Получившие прибыль игроки будут в явном меньшинстве – их всего 31,2 % от общего количества тех, кто крутил рулетку 400 раз. Я обращал на это внимание, когда ходил в казино или на скачки с небольшой группой людей. Обычно находится один человек, который выигрывает и остается в плюсе. Это ощущается как общая победа, особенно когда он покупает всем выпивку.
Итак, вот первый урок из уравнения уверенности. Победитель может считать, что у него была умная стратегия, а в реальности почти треть людей покидают казино победителями. Но случайность не должна их одурачивать. Они счастливчики, а не умельцы.
* * *
Я упустил важную деталь: сказал вам, что распределение результатов игры соответствует нормальному закону, но не объяснил почему. Объяснение восходит к работе Абрахама де Муавра 1733 года.
В своей первой книге «Доктрина шансов», посвященной азартным играм и опубликованной в 1718 году, де Муавр определял вероятность получения конкретных рук в карточных играх и выигрышных исходов при бросании костей – например, прихода двух тузов в пятикарточной руке или выпадения двух шестерок при бросании двух костей. Он вел читателя через вычисления, предлагая упражнения для улучшения понимания. Советы именно такого рода просили у него игроки, искавшие его в кофейне Old Slaughter’s.
В работе 1733 года де Муавр спрашивал своих читателей, как вычислить результат подбрасывания симметричной монеты 3600 раз. Для двух бросков монеты вероятность получить подряд два орла нетрудно найти прямым умножением: 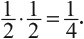 Вероятность получить три орла при пяти бросках можно найти, если выписать все возможные варианты, когда выпадает три орла (и, соответственно, две решки):
Вероятность получить три орла при пяти бросках можно найти, если выписать все возможные варианты, когда выпадает три орла (и, соответственно, две решки):
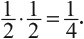 Вероятность получить три орла при пяти бросках можно найти, если выписать все возможные варианты, когда выпадает три орла (и, соответственно, две решки):
Вероятность получить три орла при пяти бросках можно найти, если выписать все возможные варианты, когда выпадает три орла (и, соответственно, две решки):ГГГРР, ГГРГР, ГГРРГ, ГРГРГ, ГРГГР, ГРРГГ, РГРГГ, РГГРГ, РГГГР, РРГГГ,
что дает нам 10 различных вариантов. Еще в 1653 году Блез Паскаль показал, что число способов взять k предметов из n (которое обозначается Cnk) определяется формулой:
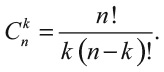
Выражение k! которое называют факториалом, определяется так: k! = k ∙ (k – 1) ∙ (k – 2) ∙ … ∙ 2 ∙ 1. В нашем примере n = 5 (пять бросков монеты и их результатов), а k = 3 (три орла, которые должны оказаться среди этих результатов). Следовательно,
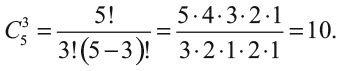
Получился тот же результат, что и при прямом переборе всех возможных вариантов. Поскольку вероятность выпадения орла на симметричной монете равна 1/2, то вероятность получить k орлов при n бросаниях монеты равна
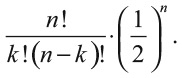
Для n = 5 и k = 3 получаем
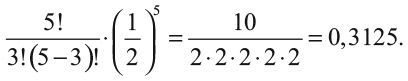
Следовательно, шансы на выпадение трех орлов при пяти бросках монеты равны 31,25 %.
Де Муавр знал о таком распределении вероятностей (сейчас оно называется биномиальным распределением), но он также понимал, насколько непрактично применять этот способ, когда n – большое число. Чтобы решить аналогичную задачу для n = 3600 подбрасываний монеты, понадобится возвести двойку в степень 3600 и вычислить 3600 ∙ 3599 ∙ … ∙ 2 ∙ 1. Попробуйте это посчитать. Такое невозможно осуществить вручную и трудно даже на компьютере.
Трюк, который проделал де Муавр, – отказ от непосредственного умножения и изучение математической формы биномиального распределения. Он вывел формулу для приближения факториалов больших чисел, а его друг, шотландский математик Джеймс Стирлинг, нашел точное значение константы в ней, и де Муавр доказал, что при достаточно больших n вышеприведенное выражение для вероятности получить k орлов при n бросках монеты приблизительно равно
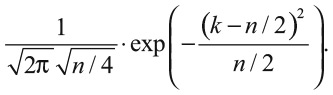
На первый взгляд кажется, что это выражение сложнее, чем исходная формула вероятности для биномиального распределения, поскольку тут есть квадратные корни, константа π = 3,14… и экспонента. Но здесь нет многочисленных умножений, необходимых для вычисления факториалов, и это главное в результате де Муавра. Можно вычислять значения для 3600 или даже миллиона бросаний, просто подставляя нужные значения k и n. Теперь де Муавр мог для вычисления использовать таблицы логарифмов или логарифмическую линейку. Технологии XVIII века способны были вести расчеты для миллиона бросаний.
Де Муавр построил первый доверительный интервал для такого события. Он показал, что шансы получить при 3600 бросаниях меньше 1740 или больше 1860 орлов составляют примерно 21 к 1, то есть вероятность получить от 1740 до 1860 орлов примерно равна 95,4 %.
В общем случае функция
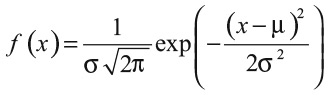
с параметрами μ и σ2 называется плотностью нормального (гауссовского) распределения, и это одна из самых важных функций в математике. Де Муавр, видимо, не осознавал всей важности своей формулы, и только в 1810-х Пьер-Симон, маркиз де Лаплас, понял весь ее потенциал. Лаплас изучал так называемую производящую функцию моментов, которая позволяет однозначно определить распределение через его моменты. Производящие функции моментов позволили Лапласу исследовать, как меняется форма распределения при сложении множества случайных результатов (например, выпадения чисел на колесе рулетки или бросания костей). Лаплас продемонстрировал замечательную вещь: независимо от того, что суммировать, по мере увеличения числа слагаемых моменты суммы всегда становятся всё ближе к моментам нормального распределения.
Потребовалось несколько лет, чтобы справиться с некоторыми хитрыми исключениями в результате Лапласа (к некоторым из них мы вернемся в ). Над теми же вопросами работали в XX веке русский математик Александр Ляпунов и финский математик Ярл Вальдемар Линдеберг. Результат, доказанный Линдебергом в 1920 году, известен сегодня под названием «центральная предельная теорема». Она говорит, что если мы складываем много независимых случайных величин (например, измерений) со средним значением h и среднеквадратичным отклонением σ, то распределение суммы этих величин будет близко к нормальному со средним значением h ∙ n и среднеквадратичным отклонением σ√n.
Чтобы оценить масштабность этого результата, рассмотрим несколько примеров. Суммируя результаты бросания игральной кости, мы получим нормальное распределение. Суммируя результаты последовательных результатов в карточных играх, рулетке или онлайн-казино, – получим также нормальное распределение. И общее количество очков в играх сезона Национальной баскетбольной ассоциации имеет нормальное распределение (см. ). И урожайность имеет нормальное распределение. Скорость движения по автостраде тоже. Как и рост людей, их IQ и результаты личностных тестов.
Везде, где результат обусловлен различными случайными факторами, можно найти нормальное распределение, поэтому уравнение 3 используют для построения доверительного интервала в любой области, где раз за разом происходит повторение одного типа действий или наблюдений.
* * *
В я показал, как игрок с преимуществом в 3 % может всего за один год превратить стартовый капитал в 1000 фунтов в сумму 57 миллионов. Если делать ставки и использовать выигрыши в дальнейшей игре, то капитал растет экспоненциально. И здесь я подошел к неизбежной ловушке для моего гипотетического игрока. Я назову этого человека Лизой. Как Лиза узнает, что ее преимущество составляет 3 %?
Нейт Сильвер, создатель и редактор сайта спортивных и политических прогнозов FiveThirtyEight, для объяснения таких ситуаций использует термины «сигнал» и «шум». В спортивных ставках значение средней прибыли (или потери) при одной ставке (величина h в уравнении 3) – это сигнал. Если у Лизы есть преимущество в 3 %, то в среднем на каждую ставку в 1 фунт она выиграет 3 пенса. Шум при ставке измеряется величиной среднеквадратичного (стандартного) отклонения σ. Как и в случае рулетки, шум в спортивных ставках гораздо больше, чем сигнал. Например, если Лиза ставит 1 фунт на какую-то команду с шансами 1/2, то она либо проиграет 1 фунт, либо выиграет 50 пенсов. С помощью можно показать, что стандартное отклонение в этом случае равно 0,71. Таким образом, шум, измеряемый стандартным отклонением (σ = 0,71), при одной ставке гораздо больше, чем сигнал (h = 0,03). Мы скажем, что отношение сигнала к шуму в нашем случае h/σ = 0,03/0,71 ≈ 1/24.
Казино знает, что у него есть преимущество, поскольку поставило рулетки, его обеспечивающие, и отношение сигнала к шуму равно 1/37. Лиза вынуждена при определении того, есть ли у нее преимущество, опираться на свой прошлый опыт. Именно здесь уравнение уверенности важнее всего для профессионального игрока. Если Лиза получила прибыль в h фунтов на ставку, а стандартное отклонение для ставки равно σ, то доверительный интервал для оценки преимущества h можно найти, поделив части уравнения 3 на n:
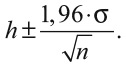
Например, если Лиза сделала 100 ставок и получила в среднем 3 пенса на каждую, этот доверительный интервал выглядит так:
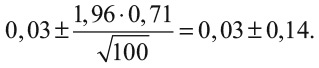
Ее преимущество может составлять 17 пенсов (0,03 + 0,14 = 0,17), но оно иногда оборачивается потерей 11 пенсов в среднем. Все возможные величины для преимущества между –0,11 и +0,17 лежат в этом 95 %-м интервале. Сделанные ею 100 ставок говорят слишком мало о том, работает ее стратегия или нет.
Поскольку доверительный интервал содержит 0, Лиза не может быть вполне уверена, что ее сигнал h положителен и ее игровая стратегия работает. Есть простое эмпирическое правило, которое она может использовать, чтобы узнать, сколько наблюдений нужно, чтобы надежно определить сигнал. Прежде всего округлим 1,96 до 2: для эмпирического правила разница между этими числами мала. Перепишем уравнение уверенности, чтобы определить условие, при котором доверительный интервал не включает ноль:
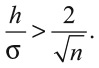
Таким образом, если мы возьмем n наблюдений, то сможем обнаружить отношение сигнала к шуму, превосходящее 2/√n.
Ниже дана таблица некоторых значений, чтобы вы представляли, как работает это правило.

Преимущество на ставках или в финансовой сфере, как правило, имеет отношение сигнала к шуму примерно 1/20 или даже 1/50; поэтому, чтобы его обнаружить, нужны тысячи и даже десятки тысяч наблюдений. Для отношения сигнала к шуму h/σ = 1/24, как на спортивных ставках у Лизы, потребуется n > 2304 наблюдений. Больше двух тысяч наблюдений – это очень много футбольных матчей. Если Лиза считает, что ее преимущество на рынке английской Премьер-лиги составляет 3 %, то ей придется для уверенности прождать шесть сезонов.
За эти шесть лет другие игроки могут наткнуться на такое преимущество и нивелировать его. Обширные операции Мэттью Бенхэма и Тони Блума постоянно направлены на поиск возможностей. Как только два этих больших Б оказываются в игре, букмекеры корректируют свои коэффициенты и преимущество исчезает. Лиза рискует, поскольку не осознает, что ее преимущество исчезло. Чтобы убедиться, что преимущество существует, требуется больше 1000 матчей. Чтобы понять, что оно исчезло, может потребоваться столько же больших убытков. Прибыль, которая экспоненциально росла, превратилась в такой же экспоненциальный ущерб.
Большинство инвесторов-любителей представляют, что им нужно отделить сигнал от шума, но мало кто понимает важность извлечения квадратного корня в полученном нами правиле. Например, для обнаружения сигнала вдвое меньшей мощности требуется вчетверо больше наблюдений, и, наоборот, увеличив число наблюдений с 400 до 1600, вы сможете заметить всего вдвое большее преимущество. Очень легко недооценить объем данных, необходимых для обнаружения крошечных преимуществ на рынках.
* * *
Я позвонил Яну в Берлин, чтобы спросить, как дела у него с Мариусом. Все шло хорошо – Мариус даже предупреждал Яна, что мне следует говорить. Однако Ян, как обычно, хотел беседовать о цифрах.
– Что я не могу тебе сказать, пока ты не поговоришь снова с Мариусом и не проверишь, что все в порядке? То, что наш оборот составляет 70 миллионов фунтов. За последний месяц мы сделали 50 000 ставок со средним преимуществом 1,5–2 %.
По сравнению с этим те 50 фунтов, которые мы ставили на чемпионате мира, были мелочью. Когда я сказал Яну, что сейчас пишу про доверительные интервалы, он вспомнил ту игровую модель, что мы построили вместе.
– Да, мы на этом заработали, – сказал он. – Однако, если честно, это не то, что мы станем использовать в будущем.
Он оказался прав: наша модель для чемпионата мира была построена на 283 наблюдениях от предыдущих турниров. Теперь же Ян создал базу данных по 15 миллиардам позиций для ставок, охватывавших многие виды спорта за последние девять лет.
– Мы сосредоточиваемся на стратегиях, где у нас есть больше 10 тысяч подтверждающих наблюдений, – сказал он.
Это давало им уверенность, что их стратегия действительно обладает долгосрочным преимуществом.
Главное преимущество Яна и Мариуса основывалось на национальных различиях. Бразильцы ожидают больше голов в своих матчах, чем забивают на самом деле. Немцы – пессимисты и предпочитают ставить на скучные 0:0.
– Норвежцы отличаются точностью, – смеется Ян. – Идеально рациональные скандинавы.
Я вспомнил свой разговор с Мариусом – как раз рациональным норвежцем – во время чемпионата мира, когда мы обсуждали, как забраться в голову игрока. Он всегда считал, что важно иметь базовое объяснение для любой стратегии ставок. Теперь у него есть одно такое объяснение: применение национальных стереотипов.
* * *
Вы ищете гостиницу на сайте TripAdvisor. Вы желаете остановиться в месте, которое получило оценки в 4 звезды или больше, и скептически относитесь ко всему, что оценено в 3,5 звезды и ниже. Сигнал, который вы здесь ищете, – разница в ползвезды. Принципы присвоения звезд на сайте TripAdvisor различны: одни с энтузиазмом раздают пятерки, а несколько недовольных вечно ставят единицы. Однако в целом шум при оценке составляет около одной звезды: большинство людей ставят 3, 4 или 5 звездочек при среднем значении, слегка превышающем 4.
Мы можем ответить на вопрос, сколько обзоров нам нужно прочитать, чтобы надежно выявить отношение сигнала к шуму, равное 1/2: либо используя , либо решив уравнение 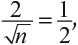 где 1/2 – отношение сигнала к шуму. Это дает нам √n = 4, что эквивалентно n = 16 оценкам на сайте. Вместо того чтобы искать среднее значение по всем сотням оценок для данной гостиницы, возьмите последние 16 и посчитайте среднее. Это даст вам одновременно и свежую, и надежную информацию.
где 1/2 – отношение сигнала к шуму. Это дает нам √n = 4, что эквивалентно n = 16 оценкам на сайте. Вместо того чтобы искать среднее значение по всем сотням оценок для данной гостиницы, возьмите последние 16 и посчитайте среднее. Это даст вам одновременно и свежую, и надежную информацию.
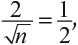 где 1/2 – отношение сигнала к шуму. Это дает нам √n = 4, что эквивалентно n = 16 оценкам на сайте. Вместо того чтобы искать среднее значение по всем сотням оценок для данной гостиницы, возьмите последние 16 и посчитайте среднее. Это даст вам одновременно и свежую, и надежную информацию.
где 1/2 – отношение сигнала к шуму. Это дает нам √n = 4, что эквивалентно n = 16 оценкам на сайте. Вместо того чтобы искать среднее значение по всем сотням оценок для данной гостиницы, возьмите последние 16 и посчитайте среднее. Это даст вам одновременно и свежую, и надежную информацию.Звездами можно оценивать не только гостиницы. Джесс не уверена в том, что правильно выбрала работу для карьеры. Она трудится в организации, занимающейся защитой прав человека. Это однозначно хорошее дело, однако руководительница просто несносна. Она целый день названивает Джесс и предъявляет непомерные требования. Ее знакомый Стив шесть месяцев встречается с Анной. Их отношения непостоянны: сейчас горячие, а в следующую минуту уже холодные. Они ужасно ссорятся, но когда разборок нет, то все замечательно.
Уравнение уверенности дает определенные указания и для Джесс – сколько ей оставаться на работе, и для Стива – сколько ему продолжать отношения с Анной, прежде чем расстаться. Сначала им нужно установить подходящие интервалы времени. Стив и Джесс решают оценивать каждый день по шкале от 0 до 5 звезд. Затем они планируют регулярно встречаться и оценивать складывающиеся ситуации.
Вечером в пятницу первой недели у Стива происходит страшная ссора с Анной, потому что она отказывается пойти с ним в компанию друзей. Стив звонит Джесс и жалуется: в результате три дня в его неделе получают по 1 звезде. Джесс напоминает ему, что не надо делать выводы слишком быстро. В конце концов, n = 7, и сигнала в шуме пока не найти. У Джесс на работе все хорошо – в основном потому, что ее проблемная начальница была в командировке, так что все дни получили по 3 и 4 звезды.
Через месяц (n = 30) они встречаются за обедом и начинают лучше понимать, как идут дела. Стив провел с Анной несколько хороших недель. В прошлый уик-энд они ездили в Брайтон, плюс к этому было несколько приятных обедов, где они отлично провели время. У Стива были целые полосы 5-звездочных дней. У Джесс все наоборот: когда ее начальница вернулась, то постоянно сердилась, кричала и теряла терпение по малейшему поводу. Дни у Джесс – это 1–2 звезды и даже найдется несколько 0-звездочных.
Прошло немногим более двух месяцев: n = 64, а 2/√n = 1/4. Теперь степень уверенности втрое выше, чем после первой недели. У Стива хорошие дни перевешивают плохие, но всё равно идут постоянные ссоры: оценки – по 3 и 4 звезды. Босс Джесс – реальная проблема, зато она работает над ценным проектом, на котором всегда хотела сосредоточиться. В лучшем случае она ставит 3 и 4 звезды, но в основном оценки – 1 и 2.
Хотя каждая неделя дает новые наблюдения, правило извлечения квадратного корня означает, что скорость получения Стивом и Джесс новой информации не пропорциональна времени, а ниже. Польза от новых наблюдений уменьшается, поэтому они решают ограничить свои обсуждения и установить срок в 100 дней (три месяца с небольшим), после чего с достаточной уверенностью окончательно решить вопрос о своем будущем.
Итак, этот день настал: n = 100, а 2/√n = 1/5. Они оглядываются не только на последние несколько недель, но и на всё, что происходило за это время. У Стива с Анной ссоры происходят реже. Они вместе стали ходить на уроки кулинарии, по вечерам с радостью готовят и приглашают к себе друзей. Жизнь хороша. Стив определяет доверительный интервал. У него получается средняя оценка h = 4,3 звезды, а стандартное отклонение σ = 1,0. Доверительный интервал для его отношений с Анной: 4,3 ± 0,2. Солидное среднее, уверенно выше четырех звезд. Стив решает прекратить жаловаться на Анну; он убежден, что нашел партнера на всю жизнь.
У Джесс ситуация не так благоприятна. Ее среднее h = 2,1 звезды. По-настоящему хороших дней было очень мало, поэтому стандартное отклонение меньше, чем у Стива: σ = 0,5. Ее доверительный интервал: 2,1 ± 0,1. По сути, у Джесс работа на две звезды. Она уже начала искать новую должность и в понедельник собирается подать заявление об уходе.
* * *
В 1964 году Малькольм Икс сказал: «Неважно, насколько сильно белые уважают и признают меня; пока такое же уважение и признание не проявляется ко всему нашему народу, его для меня не существует».
Идея, выраженная в этих словах, рождается из математики. Опыт одного человека – будь то Малькольм Икс или кто-то еще – дает нам очень мало информации. Это все равно что один раз дернуть ручку игрового автомата. Тот факт, что у Джесс был один хороший день на работе, ничего не говорит о ее карьере за долгий промежуток времени. Когда люди стали прислушиваться к Малькольму Иксу, это не значило ничего, пока они не прислушались к афроамериканцам в целом. Борьба цветных в США против дискриминации во всех формах, рассказанная через истории Малькольма Икса, Мартина Лютера Кинга и других, была и остается борьбой десятков миллионов людей.
Джоанна слышит о вакансии на своей работе. Вечером она встречает на вечеринке Джеймса и рассказывает ему об этом. Тот воодушевляется, говорит, что мечтал о такой работе, и в понедельник подает заявление о приеме. Через несколько дней Джеймс уже приступил к новой работе, а Джоанна вдруг у магазинчика с выпечкой сталкивается с Джамалом. Он спрашивает, как у нее дела, и Джоанна рассказывает, что у них только что начал работать Джеймс. Джамал воодушевляется, говорит, что мечтал о такой работе, и спрашивает Джоанну, нет ли других вакансий…
Джоанна белая. Джеймс тоже. Джамал – нет. Джоанна расистка? Нет. Она действовала бы точно так же, если бы первым встретила Джамала. Просто так случилось, что с Джеймсом она столкнулась раньше.
Однако можно еще поразмышлять о том, почему так вышло. Поскольку Джоанна и Джеймс принадлежат к одной социальной группе, они чаще встречаются и делятся информацией о возможностях. Их взаимная помощь может косвенно дискриминировать Джамала. Он не имеет доступа к тем же социальным возможностям, что Джеймс и Джоанна.
Здесь нужно быть осторожными. Мы не можем делать какие-либо выводы из истории Джоанны. У нас всего одно наблюдение, один случай ее взаимодействия с Джеймсом и Джамалом. По одному событию доверительный интервал не построить. Именно поэтому порой трудно обнаружить расовую дискриминацию. Каждый отдельный случай – всего одно наблюдение, из которого мы узнаем очень мало. Единственный способ понять роль расы в обществе – изучить множество наблюдений и построить доверительный интервал.
* * *
Моа Бёрселл, исследователь и преподаватель кафедры социологии в Стокгольмском университете, два года писала резюме и отправляла заявки на работу в Швеции. Всего она подала заявления больше чем на две тысячи разных должностей в сферах информатики, бухгалтерии, преподавания, в качестве водителя и медсестры. Однако Моа вовсе не искала работу. Она проверяла предвзятость работодателей, которым писала.
Для каждого заявления Моа создавала два отдельных резюме и сопроводительных письма, в которых описывала близкую квалификацию и опыт работы. Затем случайным образом придумывала имена для каждой пары. Одно имя звучало по-шведски, например Йонас Сёдерстрём или Сара Андерссон; второе было не шведским – скажем, Камаль Ахмади или Фатима Ахмед, указывавшие на арабское мусульманское происхождение, или Мтупу Хандуле либо Уасила Балагве, говорившие об африканском не мусульманском происхождении. Схема эксперимента Моа была эквивалентна подбрасыванию монеты. Если работодатели будут беспристрастными, они с равной вероятностью позвонят человеку со шведским и иностранным именем.
Однако этого не происходило. Например, в одном исследовании с n = 187 заявками от шведских и арабских мужчин мужчинам с арабскими именами позвонили вдвое реже, чем шведам. Такие результаты нельзя объяснить случайностью. Мы можем увидеть это, построив доверительный интервал. Арабским мужчинам позвонили 43 раза, вероятность такого звонка (сигнал) h = 43/187 = 23 %. Чтобы оценить дисперсию, будем использовать 1 для человека, которому позвонили, и 0 для того, кому не звонили. Теперь, как и в случае рулетки, вычисляем среднеквадратичное расстояние между этими величинами и h и получаем стандартное отклонение σ = 0,649. Если мы подставим эти величины в уравнение 3, то получим доверительный интервал для звонков претендентам с арабскими именами 43 ± 17,3, который содержит значительно меньшие числа, чем 79 звонков, полученных шведами.
Более того, Моа улучшила резюме арабских мужчин, добавив им от одного до трех лет опыта по сравнению со шведскими конкурентами. Это не помогало им найти работу. Более опытному арабу звонили только в 26 случаях – по сравнению с 69 звонками менее квалифицированным шведам; и это значение снова не попадает в доверительный интервал 26 ± 15,9.
«В моих результатах важнее всего то, – сказала она мне, – что их очень просто понять. С цифрами не поспоришь».
Когда Моа читает лекции по этой теме в Стокгольмском университете, она может увидеть реакцию студентов по их лицам. «Когда я смотрю на голубоглазых блондинов, они внимательно слушают. Они не думают, что это честно, но это их не трогает. Зато у людей с карими глазами, темными волосами и темной кожей я вижу другую реакцию, – продолжает она. – Это про них, их друзей, братьев и сестер. Для некоторых это означает окончательное признание. И это может быть облегчением. Они видят, что они не сумасшедшие. Их восприятие реальности подтверждается».
Эти учащиеся часто рассказывают ей о своем опыте, но другие по-прежнему молчат. «Знание о моем расследовании может травмировать, – сказала она мне. – Я вижу, что они расстроены. У них ощущение, словно им сказали: от вас мало толку, вам тут не место».
Моа аккуратно указывает, что из ее работы не следует, будто найти работу невозможно. Смысл исследования – выявить масштабы несправедливости; это не означает, что все в Швеции расисты. Оно показывает, что Камаль Ахмади и Йонас Сёдерстрём должны потратить разное количество времени, если хотят выиграть в этой лотерее вакансий.
Когда реальный Камаль Ахмади подает заявление о работе в Швеции, он не знает наверняка, с каким игровым автоматом имеет дело. Если он подал заявление, а его не вызвали на собеседование, то он не может утверждать, что его дискриминируют. Точно так же реальный Йонас Сёдерстрём не может увидеть преимущество, которое отдает ему этот игровой автомат. Он имеет квалификацию для работы; он подал заявление; ему позвонили и пригласили на собеседование. С его точки зрения, ничего неправильного не произошло.
Я изложил Моа это соображение о Камале и Йонасе, и она сказала: «Это верно, но некоторые люди иногда сами ставят эксперименты. Приехавшие из-за границы рассказывали мне, как искали работу в местном супермаркете и им сообщали, что вакансия уже закрыта. Но когда они потом просили шведского приятеля позвонить по телефону в магазин и узнать, открыта ли еще вакансия, тому сообщали, что можно прийти на собеседование».
Моа и ее коллеги разослали уже свыше 10 000 резюме, чтобы проверить различные гипотезы о шведском рынке труда. Некоторые результаты удручают: дискриминация мужчин арабского происхождения сильнее всего проявляется в ситуациях с низкоквалифицированной работой. Другие результаты вдохновляют больше: дискриминация арабских женщин выражена слабее и исчезает, если у этих женщин больше опыта работы.
Подобные исследования повторялись по всему миру со схожими результатами. Работа Моа показывает пример структурного расизма, дискриминации, которую часто трудно увидеть на индивидуальном уровне, но легко обнаружить с помощью уравнения уверенности. Недавно ведущий медицинский журнал The Lancet опубликовал доверительные интервалы для измерения социального неравенства в США – от бедности, безработицы и лишения свободы до заболеваемости диабетом и сердечными недугами. Чернокожие американцы статистически отличались от белых по всем параметрам. Свалки токсичных отходов строятся близко к районам, выделенным по расовому признаку; правительство не может предотвратить попадание свинца в питьевую воду; мелкие оскорбления на расовой почве; пониженная зарплата за одинаковую работу; целевой маркетинг сигарет и содержащих сахар продуктов; принудительная реконструкция и снос жилья; ограничения для избирателей; здравоохранение по сниженным стандартам вследствие явных или неявных предубеждений; исключение из социальных связей, которые могли бы помочь при поиске работы, – список можно продолжать. Психологическое и физическое здоровье отдельных афроамериканцев и коренных американцев ежедневно подвергается мелкой дискриминации, при этом никакого открытого расизма может и не быть.
Вернемся к Джоанне. Сталкивается ли она чаще с Джеймсами, чем с Джамалами? Чтобы это выяснить, она решает прибегнуть к уравнению уверенности. Она вспоминает всех, кому было бы интересно работать в издательстве, где она трудится: талантливых людей, затем собственных друзей, с которыми постоянно общается. Из 100 друзей Джоанны 93 белые; однако доля белых в населении США 72 %: 93–72 = 21. Ее дружеские отношения имеют перекос в расовом плане. Джоанна проверила свою привилегированность. Она пробудилась и осознала, что люди, с которыми она знакома, не отражают населения в целом и принадлежат к привилегированной группе, которая делится информацией о наличии работы в своей среде. Что Джоанне делать с этим – трудный вопрос.
Вот что я думаю. Не математический ответ на вопрос, а просто мои размышления. Джоанне не надо менять друзей. Она должна дружить с тем, с кем хочет. Но ей нужно подумать, что она может сделать в такой ситуации. Это просто. Она может написать Джамалу и другим семи приятелям из меньшинства, когда слышит о вакансии на работе, или просто поговорить с ними. У Джамала группа общения еще более перекошена: 85 из 100 черные – по сравнению с долей 12,6 % в общем населении США и 25 % в Нью-Йорке, где он живет. Одним быстрым сообщением Джоанна полностью меняет демографию людей, которые знают о вакансии.
Мои взгляды часто именуют политкорректностью. Я предпочитаю называть это статистической корректностью. Речь о статистическом осознании следующего факта: то, что мы ощущаем индивидуально, часто не отражает мир в целом. Каждый из нас как личность должен сам решить, насколько статистически правильны наши жизни и что нам с этим делать.
* * *
Уравнение уверенности, возможно, и было создано для азартных игр, но изменили его именно естественные и в итоге социальные науки. Первым участником «Десятки», осознавшим научную мощь нормальной кривой, был Карл Фридрих Гаусс, который использовал ее свойства в 1809 году, чтобы оценить ошибки в определении местоположения астероида Церера. Сегодня нормальное распределение часто называют гауссовским, что несколько несправедливо, поскольку оно описано уже во втором издании (1738) работы де Муавра «Доктрина шансов».
Статистика интегрируется в науку благодаря крупным достижениям XIX и начала XX века. После Второй мировой войны доверительные интервалы стали неотъемлемой частью научных работ, что заставило исследователей демонстрировать, почему их результаты не чистая случайность. Последняя моя научная статья содержала более пятидесяти расчетов различных доверительных интервалов. Существование бозона Хиггса было подтверждено только тогда, когда уровень статистической значимости достиг 5σ; это означает, что вероятность получить такие результаты эксперимента при отсутствии бозона Хиггса составляет 1 к 3,5 миллиона.
Изначально прогресс «Десятки» в социальных науках шел медленнее, чем в естественных. До недавнего времени карикатурное изображение кафедры социологии могло изображать мужчин в потрепанной одежде, поклоняющихся умершим немецким мыслителям, и женщин с волосами пурпурного цвета, что появились в 1970-е, чтобы встряхнуть мир постмодернистскими идеями. Они спорят и дискутируют, но никогда не приходят к согласию. Они создают определения и рамки для обсуждения и спорят дальше. Сторонние наблюдатели понятия не имеют, о чем речь. Вплоть до начала нового тысячелетия эта карикатура во многом была правдива. Статистику и количественные методы применяли, однако способом изучения общества считались социологическая теория и идеологическое обсуждение. За несколько быстро пролетевших лет «Десятка» разрушила этот старый мир. Внезапно с помощью Facebook и Instagram исследователи смогли измерить наши социальные связи. Они учли все блоги с мнениями и поняли наши методы коммуникации. Они смогли использовать государственные базы данных, чтобы определить факторы, которые заставляют нас переходить с одной работы на другую и менять место жительства. Благодаря доступности данных и статистических тестов, определивших доверительный уровень для каждого случая, раскрылась структура нашего общества.
Идеологические споры и теоретические рассуждения оказались вытесненными за пределы социальных наук. Теория ничего не стоит без данных, ее подтверждающих. Некоторые социологи старой гвардии присоединились к этой революции данных, другие же отстали, однако любой человек из университета не смог бы отрицать, что общественные науки навсегда изменились.
* * *
Не все заметили эту трансформацию социальных наук вследствие использования данных. Иногда я читаю сетевой журнал Quillette. Он гордится тем, что продолжает традиции научного диалога, восходящие к Ричарду Докинзу в 1980-е и 1990-е. Его заявленная цель – давать платформу для свободного мышления, даже для опасных идей; это означает, что он с радостью публикует мнения о гендере, расе и IQ, которые обязательно «политически корректны».
Статьи в Quillette регулярно нападают на работы в области социальных наук. Одна из любимых мишеней – политика идентичности. Недавно я закончил читать одну статью, написанную ушедшим на пенсию профессором социологии, который заявил, что общественные науки превращаются в «сумятицу и бессмыслицу». Он возражал против книги Тукуфу Зубери и Эдуардо Бонилья-Сильвы «Белая логика, белые методы: расизм и идеология». В ней исследовалось, насколько методы в социальных науках определяются «белой» культурой. Основываясь на своих сомнениях в утверждениях о «белых методах», профессор выступил со встречным заявлением, что он не смог нигде в обществе найти систематических признаков расизма. Он предположил, что наблюдаемые нами различия лучше объясняются «способностями и интересами афроамериканцев».
Авторы многих других статей в Quillette вместо рассмотрения данных стараются разжечь дискуссию с учеными-социологами и левыми активистами. Меньше внимания обращено на цифры, больше – на войну идей. Как я покажу в , внутренняя разница между биологическими расами мала (фактически такого понятия, как биологическая раса, вообще не существует), но есть множество доказательств структурного расизма в США – например, в вышеупомянутой статье в The Lancet.
Я отправил по электронной почте автору публикации в Quillette копию статьи из The Lancet с предложением ознакомиться с ее содержанием. Мы обменялись несколькими дружескими электронными письмами. Оказалось, что в сфере изучения поведения животных у нас довольно много общих интересов.
Спустя несколько недель он прислал мне свой новый труд – нападение на саму идею структурного расизма. Среди прочего он заявлял, что доказать расизм невозможно, поскольку необходимо исключить слишком много других факторов. Профессор на пенсии, похоже, упустил из виду весь смысл сбора статистических данных – выявления дискриминации по большому числу повторяющихся наблюдений. Он повторил свои утверждения о значительной разнице в биологии рас.
В ответ на американский вариант исследования резюме, проведенного Моа Бёрселл, в котором продемонстрировали предубеждение против афроамериканских имен, профессор написал: «Это расизм? Мы не знаем предыдущего опыта нанимателя. Возможно, у него есть опыт неудачного найма темнокожих».
Это расизм? Да. Здесь не нужны доверительные интервалы. К моему крайнему удивлению, через несколько месяцев Quillette опубликовал эти его размышления. К счастью, фраза «прошлый опыт неудачного найма темнокожих» была убрана. Однако статья выдерживала тот же тон, бездоказательно отрицая факты из статьи в журнале The Lancet.
Не только Quillette использует такой подход к социальным наукам. Британское интернет-издание Spiked, сетевая реинкарнация бумажного журнала Living Marxism («Живой марксизм»), регулярно нападает на гендерную политику и идею существования структурного расизма. Раздел «Культурная волна» на сайте Reddit позволяет всем желающим присоединиться к дебатам. Те же понятия пронизывают The intellectual dark web («Темная сеть интеллектуалов») – самопровозглашенное движение за свободные идеи, высказывающееся на YouTube и в подкастах за право всех быть услышанными. Участники этой группы не просто пишут о гендере и расе, а оспаривают политкорректность; и обычно дискуссия быстро переходит к этим двум «табу», как они это называют.
Король «Темной сети интеллектуалов» – Джордан Питерсон. Как и Quillette, он ведет войну против того, что считает политкорректностью, захватившей общественные науки. Питерсон утверждает, что левая идеология заставила ученых сосредоточиться на вопросах пола и расовой идентичности. Он описывает университеты как места, где боятся сказать что-то не то. В итоге это оказывает негативное воздействие на общество в целом. Белые подвергаются несправедливым нападкам за их привилегированность, а женщинам предоставляются несправедливые преимущества при приеме на работу.
Когда я летел последний раз в бизнес-классе (иногда мне это приходится делать), два парня, сидевших за мной, весь полет обсуждали, насколько хорошо одет Питерсон и как он себя ведет в споре. Я хотел обернуться и возразить, но не смог точно сказать, что неверно в их разговоре. Он хорошо одет, может аргументированно спорить и даже плакать в нужные моменты во время интервью.
Я прочитал книгу Питерсона «12 правил жизни». Она мне понравилась. Книга полна интересных историй из его жизни. Несколько хороших советов о том, как быть человеком. Приятное название. Но это не современная социальная наука. Даже близко такого нет. Это привилегированный белый мужчина, крутящий свое колесо рулетки и рассказывающий, как ему повезло.
Современное научное сообщество сильно отличается от того, как его рисует Питерсон. Я работаю со многими социологами и не думаю, что встречал хотя бы одного, кто боялся сказать то, что он думает. Наоборот. Наличие противоречивых идей, размышления о различных моделях – важная часть нашей работы.
Уравнение уверенности сдерживает современных ученых. Если мы хотим проверить нашу модель, нам надо собрать данные. Социальные науки – это уже не анекдоты или абстрактные теории. Они занимаются обнаружением структурного расизма – путем создания и рассылки тысяч резюме или тщательного изучения литературы. Это тяжелая работа, а не вопрос о том, как хорошо смотреться в костюме и изображать тщательные раздумья перед ответом на вопрос.
Левые взгляды у Моа Бёрселл проявились еще в подростковом возрасте. «Многие мои лучшие друзья того времени [начала 1990-х] имели иностранное происхождение, – говорила она мне. – Когда мы выходили по вечерам, они боялись, а некоторых преследовали неонацисты. Приходилось бегать с ними от неприятностей. Этот опыт привел меня в политику».
Когда Моа говорит о годах своего становления, она открыта и эмоциональна – при этом бесстрастна, когда рассказывает о своих научных результатах. Она также говорила мне о том, как спустя много лет один молодой борец за равенство привел к ней в университет группу иммигрантов-тинейджеров. Он хотел, чтобы Моа рассказала подросткам о своих исследованиях в области поиска работы; однако Моа боялась, что это будет неправильно воспринято. И оказалась права: когда она объяснила свои результаты, дети разозлились. «Если у нас нет будущего, зачем вообще ходить в школу?» – спросили они.
Моа была глубоко потрясена и разочаровалась в себе. «Я знаю, что многие иммигранты чувствуют себя чужаками начиная со школы, – говорила она, – и все выглядело так, будто мы привели их в университет, чтобы сказать, что и на работе их будут дискриминировать». Сообщить людям о проблеме не всегда часть ее решения.
Как и у всех социологов, у Моа есть идеалы, мечты и политические взгляды. Это ее модели мира. Когда мы находим мотивацию в наших убеждениях и опыте, в этом нет ничего ненаучного, если мы затем проверяем эти модели на соответствие данным. Когда я спросил Моа, как она начинала свою исследовательскую карьеру, она ответила: «[Социолог] Макс Вебер (если не ошибаюсь) как-то сказал – и я с ним согласна, – что вы должны выбирать тему для исследований сердцем, но затем подходить к ней максимально объективно».
Она продолжала: «Эксперименты с резюме заинтересовали меня, поскольку с результатами не поспоришь. Я изучала реальных людей, а не работала в лаборатории. В ходе этого эксперимента все контролируется, а результаты просты и понятны». Модель проверяется на данных. Моа сказала мне, что она была удивлена, когда не обнаружила гендерной дискриминации при оценке резюме работодателями, даже наоборот: женщинам звонили чаще в профессиях, связанных с компьютерами, где они представлены реже. Это шло вразрез с ее взглядами. «Но таковы факты, – заметила она. – С ними я тоже не могу спорить».
Один из вопросов, где Джордан Питерсон заметнее всего, – обсуждение гендерной разницы при оплате труда. Он правильно указывал: сам по себе тот факт, что в США на каждый доллар, выплачиваемый мужчинам, женщинам платят 77 центов, еще не свидетельствует о дискриминации. Он проводит полезное различие между равенством результатов и возможностей. Женщинам платят меньше, чем мужчинам, потому что они трудятся на более низкооплачиваемых работах – например, медсестрами. Вполне вероятно, что они могли бы найти более высокооплачиваемую работу, но они предпочли карьерный путь, отличный от мужского. Питерсон также утверждает, что женщины могут быть биологически менее приспособлены к определенным типам лучше оплачиваемой работы. В общем, по его мнению, мы не можем использовать разрыв в зарплате для заявления о наличии дискриминации; нам нужно проверять, были ли у женщин те же возможности, что и у мужчин.
Равенство возможностей – ровно то, что Моа проверяет своими экспериментами с резюме. Когда мусульмане подают заявления на работу, им звонят реже, чем шведам, и поэтому они подвергаются дискриминации по возможностям. Точно так же результаты Моа показывают равенство в возможностях для шведок при рассылке резюме. В этом случае утверждение Питерсона об отсутствии дискриминации по возможностям справедливо.
Но равенство по результатам можно измерить одним числом (например, гендерный разрыв в оплате труда), а вот с равенством по возможностям так не получится. Есть много способов помешать женщинам полностью реализовать свой потенциал, и нужно исследовать много возможных препятствий.
К счастью, социологи стремятся определить их. В 2017 году Катрин Ауспург и ее коллеги опросили 1600 жителей Германии, предоставив им краткое описание возраста, пола, стажа и роли на работе гипотетической личности, а затем спросив, насколько указанная зарплата справедлива. Оказалось, респонденты склонны думать, что женщинам переплачивают, а мужчинам недоплачивают. В среднем они (как мужчины, так и женщины) считали, что женщинам нужно платить 92 цента на каждый доллар, выплачиваемый за ту же работу мужчинам. В то же время на прямой вопрос, следует ли мужчинам и женщинам платить одинаково, подавляющее большинство ответило утвердительно. Так что есть большая разница между тем, что мы говорим, и тем, как действуем на практике. Респонденты в этом эксперименте даже не осознавали, что фактически рекомендуют, чтобы женщинам платили меньше мужчин за одинаковую работу.
В одном исследовании 2012 года выявлено предвзятое отношение ученых к женщинам при оценке резюме на должность лаборанта. Снова оказалось, что и мужчины, и женщины при рассмотрении резюме от соискательниц-женщин считают их менее компетентными. Женщины, которым преподают только профессора-мужчины, с меньшей вероятностью продолжат изучать предмет, чем если бы у них были профессора-женщины. Один эксперимент со старшеклассниками показал, что девочки, занимающиеся наукой в классах, где имеются такие стандартные вещи, как предметы из вселенной «Звездных войн», технические журналы, видеоигры, научно-фантастические книги и т. д., гораздо реже продолжают проявлять интерес к преподаваемому предмету, чем в случае занятий в классах с менее стандартной обстановкой (изображения природы, картины, ручки, кофеварка, журнал общего содержания и т. д.). В канадских средних школах девочки, как правило, считают себя слабее в математике, чем мальчики, хотя на экзаменах демонстрируют такие же результаты. В ходе эксперимента с переговорами, проведенного в одном американском университете, оказалось, что женщины настолько же эффективны в этом деле, как и мужчины, когда действуют от имени другого лица, но менее эффективны, когда говорят от собственного имени. Эти различия объясняются страхом отрицательной реакции, если они победят в споре, – тем страхом, который мужчины так остро не ощущают.
Это всего лишь некоторые из многочисленных исследований, которые рассматривали Сапна Черян и ее коллеги – с целью установить препятствия, относящиеся к гендеру. Женщинам и девушкам труднее свободно выражать свое мнение; их недооценивают и мужчины, и другие женщины; им предлагают меньше ролевых моделей; они неявно подвергаются дискриминации, когда подают заявки на определенную работу: это статистически верный способ оценить наши школы и рабочие места. Поскольку большинство, включая Джордана Питерсона, согласны с тем, что нужно стремиться к равенству возможностей, ответ прост: нам нужно информировать людей о результатах тех работ, которые выявляют предрассудки в нашем обществе.
Как ни странно, Питерсон делает противоположный вывод. Он нападает на научные исследования по вопросам меньшинств и гендера, заявляя, что те левые и что их проводят марксисты. Здесь он неправ. Социологи – например, Моа Бёрселл, Катрин Ауспург и Сапна Черян – осознанно изучают возможности, а не результаты. Возможно, их мотивация – желание добиться справедливости для всех, но именно поэтому очень важно, чтобы на их работу не влияли политические взгляды, которых они придерживаются. Цель всех вышеупомянутых и многих других работ – выяснить, где нет равенства возможностей, чтобы решить проблему. Нет никаких свидетельств идеологической предвзятости этих исследователей.
Питерсон никогда не упоминает об этих работах. Он сосредоточивается на психологических различиях между мужчинами и женщинами. В январе 2018 года в интервью Кэти Ньюман в новостях британского канала Channel 4, которое позже стало вирусным на YouTube, он утверждал: «Покладистые доброжелательные люди вежливы и проявляют сочувствие. Им меньше платят, чем неприятным людям, за ту же работу. Женщины более покладисты, чем мужчины».
Есть несколько причин, почему подобные психологические объяснения не так убедительны, как проверка конкретных моделей с доверительными интервалами. Рациональные основания, стоящие за прямыми и зависящими от контекста вопросами вроде «Как бы вы оценили это резюме?» или за наблюдением, как мужчины и женщины ведут переговоры, заключаются в том, что, понимая действия отдельных людей, мы можем объяснить, как возникает неравенство. А вот покладистость и доброжелательность определяются через тесты самооценки, когда люди отвечают на общие вопросы вроде «Я проявляю сочувствие к эмоциям других людей». Сказать, что кто-то «доброжелателен» и «покладист», – всего лишь способ суммировать ответы из таких анкет. Вовсе не очевидно, почему покладистость – препятствие для повышенной зарплаты. Это работает в обе стороны. Может быть, покладистые люди получают вознаграждение за свое дружелюбие или они плохие переговорщики? Покладистость может оказывать разное влияние в зависимости от карьеры, навыков, необходимых для работы, и стажа.
Сами по себе личностные тесты не дают никакого объяснения, поэтому для проверки связи покладистости и зарплаты требуются дополнительные изыскания. Одно исследование 59 недавних выпускников в США показало, что на ранних этапах карьеры покладистые люди действительно получают пониженную зарплату. Но оно также установило, что женщинам платили значительно меньше, чем мужчинам. Даже с учетом всех остальных черт характера, общих умственных способностей, эмоционального интеллекта и успехов покладистость была единственным фактором, который помогал объяснить разрыв в зарплате, и то лишь отчасти. Неприятным женщинам платили все равно меньше, чем неприятным мужчинам, а покладистым мужчинам – больше, чем покладистым женщинам. Это исследование показало, что – вопреки тому, что Питерсон говорил в интервью Channel 4, – не связанные с гендером факторы не могут объяснить разрыв в зарплате.
Отсутствие четкой модели того, как личность влияет на зарплату, очень затрудняет конкретный разговор о том, как личность влияет на возможности. Даже если мы установили, что существует дискриминация покладистых людей в отношении зарплаты, а не прямая дискриминация женщин, нам все равно нужно искать ответ на вопрос, справедливо это или нет. Какие-то соображения (например, что покладистые люди недостаточно эффективно действуют в интересах своей компании) можно счесть справедливыми, а другие (руководство извлекает выгоду из покладистости сотрудников, платя им меньше) – нет. Разговор о личных качествах в общих чертах не помогает нам понять реальные проблемы.
Также важно ближе присмотреться к тому, что на самом деле подразумевает Питерсон, когда говорит, что женщины покладистее мужчин. Здесь мы можем применить уравнение уверенности. Психологи проводили личностные исследования на сотнях тысяч людей. Как мы видели раньше в этой главе, чем больше наблюдений, тем лучше мы можем обнаружить сигнал, скрытый в шуме. Например, если мы провели n = 400 анализов людей, то обнаружим разницу даже при отношении сигнала к шуму 1/10. Имея много данных, мы способны использовать уравнение уверенности для определения даже очень малых различий в покладистости мужчин и женщин. И ровно их мы обнаруживаем, когда дело касается личных качеств. Отношение сигнала к шуму для покладистости – той черты, которая сильнее всего отличает мужчин от женщин, – составляет примерно 1/3. На каждые три единицы шума приходится одна единица сигнала.
Чтобы понять, насколько слаб сигнал, представьте, что из популяции выбираются наугад одна женщина и один мужчина. Вероятность того, что женщина более покладиста, составляет всего 63 %. Подумайте, что это означает на практике. Вы стоите перед закрытой дверью и собираетесь познакомиться с Джейн и Джеком. Разумно ли для вас войти в комнату и сказать: «Джейн, я думаю, что ты больше склонна соглашаться со мной, чем Джек, потому что ты женщина», а Джеку сказать: «Ну а с тобой мы, видимо, поспорим»?
Нет. Это статистически неверно. Вероятность ошибки составляет 37 %.
Питерсон утверждает (например, в скандинавском ток-шоу Skavlan), что психологи «усовершенствовали, по крайней мере отчасти, измерение личностных качеств с помощью улучшенных статистических моделей». Затем он упоминает огромное количество анкет по личностным характеристикам, которые применялись к сотням тысяч людей. Потом он справедливо признаёт, что женщины и мужчины больше схожи, чем различны. Потом просит нас подумать, «в чем главные различия», и говорит, что «мужчины менее покладисты… а женщины больше склонны к негативным эмоциям или невротизму».
Хотя это не совсем неверно, рассуждение несколько обманчиво. Подразумевается, что ученые выявили масштабные гендерные различия специфичного рода, использовав большие объемы данных. Правильная интерпретация такова: исследователи придумали сотни различных способов опрашивать мужчин и женщин, как они себя видят, и опросили сотни тысяч людей, но почти все исследования не выявили никаких гендерных различий в личностных качествах. По сути, самый примечательный результат последних тридцати лет личностных исследований – гипотеза о гендерном сходстве. Эта гипотеза, впервые высказанная в 2005 году в журнале American Psychologist профессором психологии Висконсинского университета в Мадисоне Джанет Хайд, которая занимается исследованиями гендера и женщин, не утверждает, что мужчины и женщины одинаковы. Она говорит, что между личностными качествами есть очень мало статистических различий, зависящих от гендера. Хайд рассмотрела 124 теста личностных различий и установила, что в 78 % из них обнаружены несущественные или небольшие различия между гендерами (отношение сигнала к шуму меньше 0,35). Эта гипотеза выдержала проверку временем: спустя десять лет новый независимый обзор установил, что только 15 % тестов дали для связи между гендером и личностью отношение сигнала к шуму больше 0,35.
В плане невротизма, экстраверсии, открытости, позитивных эмоций, грусти, гнева и многих других черт мужчины и женщины различаются очень слабо или не различаются вообще. В более позднем обзоре Хайд обнаружила, что гендерные различия также малы в математических способностях, навыках устной речи, добросовестности, реакции на вознаграждение, непрямой агрессии, использовании предположительных слов, отношении к мастурбации и внебрачным связям, эффективности руководства, самоуважении и самооценке. Сильнее всего полы различаются по интересу к вещам и людям, физической агрессии, использованию порнографии и отношению к случайному сексу. Оказывается, некоторые предрассудки всё же верны. Наши личностные характеристики сильно разнятся. Мужчины отличаются друг от друга. Женщины тоже. Но в целом статистически неверно утверждать, что личностные характеристики мужчин и женщин очень разные.
Опасность заявлений Джордана Питерсона в том, что исследования гендера каким-то образом извращены «левыми» или «марксистскими» силами. Всё наоборот. Джанет Хайд, имеющая диплом бакалавра по математике, – часть статистической революции, измеряющей равенство возможностей и изгоняющей идеологическое мышление из психологии и социальных наук. За свои работы она получила несколько наград, включая три от Американской психологической ассоциации – крупнейшей научной и профессиональной организации психологов в США. Гендерные различия изучены так подробно, что документировано даже мельчайшее различие. Аналогичные результаты были получены в нейробиологии: различия среди представителей каждого пола гораздо больше, чем различия между женским и мужским мозгом. Ирония в том, что Питерсон для поддержки своей точки зрения с идеологической мотивацией может выковыривать подходящие ему результаты только из этого обширного массива строгих исследований.
Уравнение уверенности учит нас заменять байки наблюдениями. Никогда не полагайтесь на историю одного человека – даже собственную. Когда вы побеждаете, тщательно поразмыслите, длилась ли полоса успехов достаточно долго, чтобы вы могли ее приписать своему умению. Всегда есть тот, кому везет, и, возможно, на этот раз этим человеком были вы. Ищите другие истории и собирайте статистику. По мере того как вы изучаете информацию, рассуждайте в рамках правила о квадратном корне из n: чтобы обнаружить сигнал вдвое слабее, нужно вчетверо больше наблюдений. Если вы «вверху» и это статистически лучше, чем у окружающих, проверьте свое привилегированное положение с помощью статистического интервала. Будьте корректными: осознавайте плюсы и минусы того, что у вас есть. Будьте уверенными, не обманывая себя, а понимая, как именно общество формирует вашу жизнь. Только тогда вы сможете найти преимущество и заявить о нем.
Назад: Глава 2. Уравнение суждений
Дальше: Глава 4. Уравнение умений

