Глава 2. Уравнение суждений

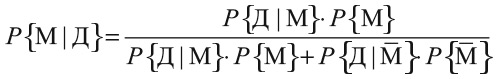
Мой друг Марк руководит командой финансовых трейдеров, и все они владеют математическими методами. Марк заметил, что у лучших из них есть общая черта – способность реагировать на новую информацию и обрабатывать ее. Когда происходят какие-то события, они быстро подстраиваются к новой реальности.

Эти люди рассуждают не в абсолютных характеристиках – «та компания получит прибыль в следующем квартале» или «тот стартап провалится», – а в терминах вероятностей: «компания получит прибыль с вероятностью 34 %» или «для этого стартапа риск неудачи составляет 90 %». Когда поступает новая информация – например, CEO вынужден уйти в отставку или бета-версия, выпущенная стартапом, пользуется успехом, – они корректируют эти вероятности: 34 % превращаются в 21 %, а 90 % – в 80 %.

Аналогичные истории я слышал и от Джеймса, знакомого из индустрии азартных игр. Там в ходу варианты уравнения ставок, но при таком количестве денег на кону приходится принимать быстрые решения о том, годится ли их модель для предстоящих футбольных матчей. Что делать, если за час до игры стартовый состав команды меняется и предположения, лежащие в основе модели, становятся недействительными?

– Именно в такие моменты вы узнаете, кто действительно хороший специалист, – говорил Джеймс. – Он не реагирует резко. При одном изменении в стартовом составе ставка не меняется; при двух – четырех специалист оценивает разные возможности; при пяти или больше все ставки снимаются.

Чтобы научиться думать как эти аналитики, вам нужно ставить себя в эмоционально напряженную ситуацию. К примеру, на земле большинство из нас понимают, что полеты не опасны: вероятность попасть в авиакатастрофу со смертельным исходом не превосходит 1 на 10 миллионов. Но в воздухе все ощущается иначе.

Представьте, что вы опытный путешественник, уже летавший сотню раз. Однако этот рейс иной. При снижении самолет начинает грохотать и трястись – такой болтанки вы еще не ощущали. Женщина рядом хватает воздух ртом; мужчина, сидящий через проход, стискивает колени. Все вокруг явно напуганы. Что это? Может ли разворачиваться наихудший сценарий?

В подобных ситуациях математик глубоко вдохнет и соберет всю доступную информацию. Назовем катастрофой худший сценарий – крушение со смертельным (для вас) исходом. Обозначим его вероятность как P{катастрофа}. По статистике, P{катастрофа} = 1/10 000 000, или 1 на 10 миллионов.

Чтобы понять, как события зависят друг от друга, обозначим P{тряска|катастрофа} – вероятность, что самолет трясется, при условии, что произойдет катастрофа: «тряска» означает «самолет трясется», а вертикальная линия – «при условии». Сделаем разумное предположение, что P{тряска|катастрофа} = 1, то есть перед любой катастрофой самолет трясет.

Нам также необходимо знать P{тряска|не катастрофа} – вероятность болтанки при безопасном приземлении. Здесь вам придется опираться на свои ощущения. Раз это самый страшный рейс из сотни ваших полетов, то лучшей оценкой будет P{тряска|не катастрофа} = 1/100.

Эти вероятности полезны, но вы желаете знать не их. Вам нужна величина P{катастрофа|тряска}, или вероятность того, что произойдет крушение, при условии, что самолет так трясется. Эту величину можно найти с помощью теоремы Байеса.

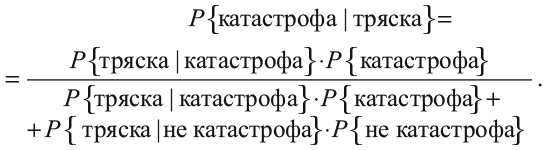
Символ ∙ означает умножение. Вскоре я объясню, откуда появляется это уравнение, а пока просто примем его. Оно было рассмотрено преподобным Томасом Байесом в середине XVIII века и с тех пор используется математиками. Подставив все нужные числа в наше уравнение, мы получаем:

Даже если это самая сильная болтанка, которую вы когда-либо испытывали, шансы погибнуть составляют 0,00001. Вы благополучно приземлитесь с вероятностью 99,99999 %.

То же рассуждение применимо к целому ряду различных, казалось бы, опасных ситуаций. Даже если во время купания на австралийском побережье вам кажется, что вы видите в воде нечто пугающее, вероятность того, что это акула, крохотная. Вы можете волноваться, когда ваши близкие возвращаются поздно домой, а вам не удается с ними связаться, но вероятнее всего, что они просто забыли зарядить телефон. Многое из того, что мы считаем новой информацией – тряска самолета, неясные фигуры в воде или отсутствие звонков, – не так уж страшно, если подходить к проблеме правильно.

Теорема Байеса позволяет вам верно оценивать важность информации и сохранять спокойствие, когда все вокруг паникуют.

Я смотрю на мир способом, который именую кинематографическим: часто (и один, и даже в компании) прокручиваю в голове фильмы о своем будущем. Это не один фильм или одно будущее; это много фильмов с разными поворотами сюжета и концовками. Объясню на примере самолета.

Когда я взлетаю и приземляюсь на самолете, то вижу катастрофу, которую описал выше. Если лечу с семьей, то представляю, как держу руки детей, говорю, что люблю их, чтобы они не беспокоились. Я воображаю, как мы держимся вместе, когда падаем навстречу смерти. Когда я лечу один, а вокруг только незнакомцы, то смотрю другой фильм: наблюдаю целые годы, которые моя семья проведет без меня. Похороны проходят быстро, и я вижу, как моя жена в одиночку справляется с детьми и рассказывает им истории о нашей совместной жизни. Этот фильм неописуемо печален.

Подобные картины крутятся непрерывно и параллельно в какой-то области мозга выше левого глаза. По крайней мере, я так ощущаю. Большинство фильмов не настолько драматичны. У меня встреча с редактором книги, и в голове проигрывается дискуссия: я обдумываю, что ей скажу. Провожу какой-нибудь семинар и вижу, как излагаю материал, представляя сложные вопросы. Многие такие фильмы абстрактны: я прохожусь по научной статье, которую пишу; смотрю на структуру диссертации одного из моих аспирантов; работаю над какой-то математической задачей. Кинокартины такого рода не будут смотреться на большом экране. Они набиты цифрами, техническими терминами и научными ссылками. Мне они нравятся, но я очень специфическая аудитория.

Хочу убедиться, что у вас не сложилось впечатления, будто я воображаю себя всевидящим оракулом. Вовсе нет. Фильмы, которые я создаю, фрагментированы. Нет деталей, нет наполненности реальностью. И, что крайне важно, почти все они не соответствуют действительности. Редактор книги ведет дискуссию в другом направлении, и я забываю все свои вопросы. В цепочке рассуждений в научной статье возникает дыра, и я не могу ее исправить. В первой строке моих математических выкладок обнаруживается ошибка в вычислениях, и результаты оказываются неверными.

Психологи изучали методы, с помощью которых люди смотрят на мир и конструируют повествования о будущем, однако научное описание процесса здесь не главное. Важно ваше представление о том, как вы видите будущее. В форме текстов, фильмов или компьютерных игр? Фотографий, звуков или запахов? Это абстрактное ощущение или вы визуализируете реальные события? Постарайтесь определить метод своих размышлений о вещах. Ваш взгляд на мир должен оставаться вашим личным – я не хочу его менять. Я бы не вынес, если бы кто-нибудь предложил мне отключить мои фильмы. Мой «кинематограф» – часть меня.

Математика участвует в моем мышлении, помогая мне организовать мою коллекцию фильмов. Авиакатастрофа – хороший пример. Когда прокручиваю фильм с катастрофой, я также оцениваю вероятность того, что такое событие произойдет, и считаю ее обнадеживающе низкой. Это не останавливает прокрутку фильма. Я по-прежнему боюсь летать или плавать в океане, но это помогает мне сосредоточиться. Вместо того чтобы бояться, думаю о том, как много значит для меня семья и почему мне нужно меньше путешествовать, а больше плавать в океане.

Научный термин для фильмов, которые я проигрываю в голове, – «модель». Крушение самолета – модель, нападение акулы – модель и план исследовательской работы – тоже. Модели могут быть чем угодно – от смутных мыслей до более формально определенных уравнений, подобных тому, что я создал для ставок на чемпионате мира. Первый шаг к математическому подходу к миру – понять, как мы используем модели.

У Эми начался новый курс в колледже, и она задается вопросом, с кем стоит дружить, а от кого держаться подальше. Она доверчивый человек, и ее «фильм» в голове – о людях, которые рады ей и ведут себя мило. Но Эми не совсем наивна. Она уже знает, что не все люди приятны, и «стервозный» фильм в ее голове тоже есть. Не судите Эми за термины – в конце концов, она держит мысли при себе. Именно поэтому, когда Эми знакомится с Рэйчел – девушкой, сидящей рядом, – она полагает, будто шансы на то, что Рэйчел окажется стервой, довольно малы: скажем, примерно 1 из 20.

Я не думаю, что Эми при встрече с другими определяет вероятность «стервозности». Я определяю это число, чтобы вы лучше понимали ситуацию. Можете на секунду задуматься и решить, какая доля окружающих стервозна. Надеюсь, она меньше 1/20, но вы можете выбрать свои числа.

В первое утро Рэйчел и Эми вместе разбирают лекцию. Эми плохо разбирается в деталях, потому что в ее школе не давали знаний, необходимых для понимания концепций, о которых говорит преподаватель. Рэйчел выглядит терпеливой, но Эми осознаёт, что та несколько раздосадована. Почему Эми не может учиться быстрее? Затем, после обеда, происходит ужасное. Эми сидит в одной из кабинок в туалете, рыщет по интернету с помощью смартфона и думает о своих делах. Она слышит, как входят Рэйчел и еще одна девушка.

– Эта новая девица тупа, – говорит Рэйчел. – Я пыталась ей объяснить «культурную апроприацию», а она ничего об этом не знала. Она думала, что это когда белые люди учатся играть на бонго!

Эми сидит неподвижно, не издает ни звука и ждет, пока девушки уйдут. Что она должна думать?

Большинство из нас на месте Эми огорчились бы, разозлились, а может, и то и другое. Но стоит ли? Да, Рэйчел явно поступила неправильно. У Эми первый день учебы, и лить грязь на человека нехорошо. Но вопрос в другом: должна ли Эми, несмотря на этот проступок Рэйчел, простить ее и дать ей еще один шанс?

Да. Да. Да. Должна! Обязана! Мы должны прощать такое. И не раз, а много. Нужно прощать людей за глупые комментарии, за то, что они обзываются за нашей спиной и не замечают нашего присутствия.

Но почему? Потому что мы хорошие? Потому что всегда позволяем наступать на себя? Потому что слабы и не можем за себя постоять?

Нет. Нет. Нет. Вовсе не поэтому. Нам нужно прощать их, потому что мы рациональны и верим в логику и разум. Мы хотим быть справедливыми. Мы знаем теорему преподобного Байеса. А второе уравнение говорит нам, что это – единственно верное действие.

И вот почему. Теорема Байеса – связь, которую нам нужно установить между моделью и данными. Она позволяет нам проверить, насколько хорошо наши картинки соотносятся с реальностью. В примере, который мы разбирали в начале главы, мы рассматривали вероятность P{катастрофа|тряска} того, что самолет разобьется, при условии, что он попал в болтанку. Эми желает знать P{стерва|грубость}, и логика здесь та же.

Катастрофа и стерва – модели в наших головах. Это наши представления о мире, которые принимают форму мыслей или (в моем случае) фильмов. Тряска и грубость – данные, которые есть в нашем распоряжении. Это нечто осязаемое, то, что происходит, что мы можем ощущать. Значительная часть прикладной математики включает сопоставление моделей с данными, столкновение наших мечтаний с суровой реальностью.

Будем использовать букву M для модели и Д для данных. Мы хотим знать сейчас вероятность того, что модель верна (Рэйчел – стерва), при условии истинности данных (грубый комментарий в туалете). Имеем:

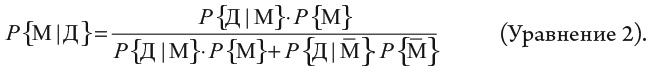
Чтобы понять уравнение (формулу Байеса), лучше всего рассмотреть по отдельности компоненты правой части.

Числитель (часть над дробной чертой) – произведение двух вероятностей, P{М} и P{Д|М}. Множитель P{М} – вероятность того, что модель истинна, до того, как произошло некое событие (статистическая вероятность крушения самолета или оценка Эми, что встреченный ею человек стервозен; в последнем случае – 1/20). Эту величину Эми знала прежде, чем отправилась в туалет. Второй множитель, P{Д|М}, касается того, что произошло в санузле. Это вероятность, что Рэйчел оскорбит Эми, если она в самом деле стерва, или – в общем случае – того, что мы наблюдаем некоторые конкретные данные, если наша модель верна. Трудно оценить это число количественно, поэтому будем считать его эквивалентом броска монетки: P{Д|М} = 0,5. Рэйчел не каждый раз при посещении туалета злословит о сокурсницах. Минимум 50 % времени стервы тратят на разговоры о чем-то еще.

Мы перемножаем вероятности, чтобы найти вероятность того, что произошли одновременно оба события. Например, если я бросаю две игральные кости и хочу найти вероятность выпадения двух шестерок, то я определяю вероятность 1/6 для выпадения шестерки на первой кости, вероятность 1/6 для шестерки на второй, а затем перемножаю их и получаю вероятность выпадения шестерок на обеих костях: 1/6 ∙ 1/6 = 1/36. Тот же принцип применяется и здесь: числитель – вероятность того, что Рэйчел стерва и она отпустила стервозный комментарий при посещении туалета.

Итак, числитель описывает Рэйчел как стерву, но мы должны также рассмотреть альтернативную модель, в которой она хороший человек. Это делается в знаменателе дроби справа. Рэйчел может быть стервой, сделавшей стервозный комментарий (M), или хорошим человеком, допустившим ошибку (M–). Черта над буквой означает противоположность или дополнение. В нашем случае дополнение к «быть стервой» – «быть не стервой», «быть хорошим человеком». Обратите внимание, что первое слагаемое в знаменателе совпадает с числителем, P{Д|М} ∙ P{M}. Второе, P{Д|M–} ∙ P{M–}, – вероятность того, что Рэйчел сделала свое грязное замечание при условии, что она не стерва, умноженная на вероятность того, что она хороший человек. Мы охватили все возможные объяснения тех данных, что получила Эми, сидя в кабинке туалета. Теперь можно найти P{M|Д} – вероятность модели при условии этих данных.

Если Рэйчел не стерва, то она хороший человек, поэтому P{M–}=1–P{M}=0,95. Теперь нужно определить вероятность, что хороший человек совершает ошибку и говорит гадость. Возможно, у милой Рэйчел был неудачный день – у всех такое случается. Предположим, что один раз из десяти у хороших людей бывает плохой день и они говорят то, о чем потом жалеют. Иными словами, пусть P{Д|M–}=0,1 (см. рис. 2).

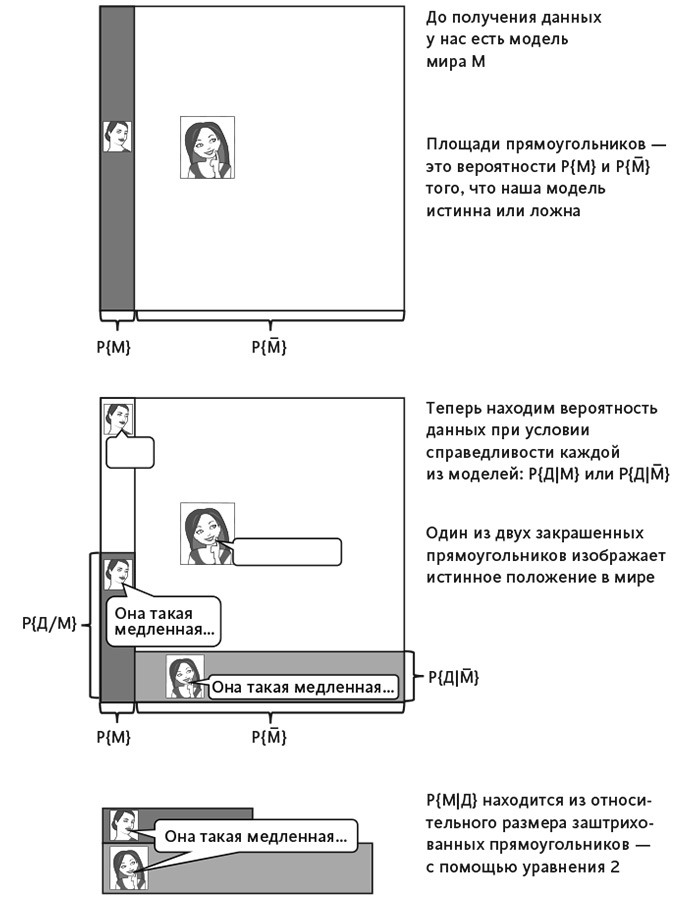
Рис. 2. Иллюстрация теоремы Байеса

Осталось только произвести подсчет – точно так же, как с крушением самолета, но с другими числами:

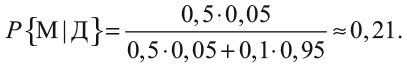
Вероятность того, что Рэйчел – стерва, примерно 1/5. Именно поэтому Эми стоит простить ее. С вероятностью 4/5 она хороший человек. Было бы нечестно судить девушку только по одному действию. Эми не следует упоминать, что она слышала Рэйчел, или допустить, чтобы эти слова влияли на их общение. Лучше ждать и смотреть, что произойдет завтра. С вероятностью 80 % к концу года они будут вместе смеяться над этим случаем в туалете.

И еще один совет Эми, съежившейся за дверью туалета. Возможно, в то утро она не работала с максимальной отдачей. Может, в следующий раз ей нужно лучше стараться и уж точно не стоит сидеть в уборной и развлекаться с телефоном. Но помните, что Байес прощает прегрешения. Эми должна применять ту же формулу и к себе. Теорема Байеса предлагает ей медленно корректировать свое мнение о себе и не особо огорчаться из-за конкретных событий.

Вы продукт всех своих действий, а не результат одной или нескольких ошибок. Применяйте к себе то же рациональное прощение, которое Байес просит вас применять к другим.

Первый урок, который нужно извлечь из формулы Байеса (уравнения суждений), – не надо торопиться с выводами. Числа, которые я использовал в примере, влияют на результат, но не на саму логику. Вы можете спросить себя: какая доля людей, по-вашему, в целом хорошие? Как часто хорошие люди совершают ошибки? И как часто стервы поступают по-свински? Подставьте свои цифры в уравнение, и вы придете к тому же заключению: нужно больше, чем один грязный комментарий, чтобы поставить на человеке клеймо «стерва» или «сволочь».

Иногда мой руководитель ведет себя как козел. Иногда моим студентам как будто не хватает сосредоточенности. Порой кто-то из коллег хочет приписать себе мою идею, заявляя, что придумал это первым. Иногда председатель комиссии, где я состою, кажется мне неорганизованным: он тратит мое время на бесполезный неэффективный обмен электронными письмами. В таких ситуациях я использую уравнение суждений. Но я не вычисляю вероятность того, что каждый из моих коллег – скотина, рассеянный или некомпетентный. И не позволяю разовым событиям определять свои ощущения. Если я вижу, что некто, с кем я работаю, совершил ошибку, я жду развития ситуации. Вполне может оказаться, что неправ был я.

Мы не можем понять «Десятку» без раскрытия ее истории и философии. История «Десятки» – рассказ о небольшой группе людей, которые передавали секреты рационального мышления из поколения в поколение. Они ставили масштабные вопросы. Они хотели знать, как мыслить яснее и точнее, уметь оценивать истинность того, что говорят люди. Они даже задавались вопросом, что значит быть истинным или ложным. Это история о действительно важных вопросах: природе реальности и месте этих людей в ней.

Это также рассказ о религии, о том, что такое хорошо и что такое плохо, об этике, о добре и зле.

Наша первая остановка – 1761 год. Валлийский философ Ричард Прайс обнаружил в бумагах недавно умершего друга (того самого Томаса Байеса) эссе, полное математических символов и философских размышлений, и один вопрос звучал так: как на основе данных о предыдущих событиях оценить вероятность того, что подобное произойдет снова? Прайс опубликовал его со своим приложением, где просил читателя представить «человека, только что появившегося в этом мире, который заключает из своих наблюдений за порядком и ходом событий, какие силы и причины в нем действуют». Спрашивается, как такой человек должен рассуждать, увидев восход в первый раз, во второй и в третий. Что он должен сказать о вероятности того, что солнце встает каждый день?

Вывод примечателен. Ежедневный восход солнца не должен привести нашего «только появившегося» человека к выводу, будто солнце будет вставать всегда. Наоборот, его умоляют быть очень осторожным с этим событием – даже после сотни восходов и целой жизни восходов. Ничто не должно быть само собой разумеющимся.

«Только появившемуся» человеку предлагалось дать оценку вероятности ежедневного наступления восхода с помощью некоторого параметра θ. Перед первым восходом человек не имеет никаких априорных представлений о солнце и должен считать все значения параметра θ равновозможными. В этот момент одинаково вероятно, что солнце поднимается каждый день (θ = 1), встает в половине дней (θ = 0,5) или только один раз из ста (θ = 0,01). Величина θ может принимать бесконечное число значений из интервала от 0 до 1 (все вероятности находятся в этом промежутке). Например, она может оказаться 0,8567, 0,1234792, 0,99999 и т. д. При этом число десятичных знаков любое, точность произвольна.

Далее человеку предлагается определить, какое значение тот сочтет минимальной правдоподобной вероятностью того, что солнце восходит ежедневно. Если человек думает, что шансы на восход превышают 50 %, то θ > 0,5. Если он считает, что они превысят 90 %, то θ > 0,9.

Теперь представим, что человек увидел 100 восходов подряд и пытается сделать из этого вывод о вероятности восхода в один день: он заявляет, что солнце поднимается чаще 99 раз из 100. Иными словами, он дает оценку θ > 0,99. Выражение P{θ > 0,99|100 восходов} определяет вероятность того, что он прав в своей оценке. Байес показал с помощью определенной разновидности уравнения 2, что P{θ > 0,99|100 восходов} = 1–0,99¹⁰⁰⁺¹ ≈ 63,8 %. Соответственно, с вероятностью 36,2 % наш человек ошибается и солнце встает реже, чем он полагает.

Если человек прожил 60 лет и видел восход солнца каждый день, он мог бы определенно быть уверен, что вероятность восхода солнца каждый день превышает 99 %. Но если он желает быть уверенным, что вероятность восхода солнца превосходит 99,99 %, мы бы посоветовали проявлять осторожность: 1–0,9999^365×60+1 ≈ 88,8 %. Так что остается еще 11,2 %, что он ошибается. Мы заставляем новоприбывшего обитателя мира определить свою модель, высказать минимальное возможное значение θ, а затем сообщаем ему вероятность, с которой он прав в своем предположении.

Ричард Прайс осознал, что формула Байеса связана со спорами о чудесах, которые происходили в XVIII веке. Как и Байес, Прайс был священником и интересовался, как новые научные открытия того времени могут сочетаться с чудесами, в которые он верил после чтения Библии.

Десятилетием ранее философ Дэвид Юм утверждал, что «никакое свидетельство недостаточно для установления чуда, кроме такого, ложность которого была бы большим чудом, нежели тот факт, который оно стремится установить». Эти слова можно рассматривать как обращение к уравнению суждений. Он просит нас сравнивать модель M, что чудеса происходят, с альтернативной моделью M–, что они не происходят. Юм говорит, что, поскольку мы никогда раньше не были свидетелями чуда, P{M–}близка к 1, а P{M} очень мала, поэтому, чтобы убедить нас в обратном, понадобится очень серьезное чудо, у которого будет очень большая P{Д|M} и маленькая P{Д|M–}. Аргументация Юма очень близка к моим рассуждениям о болтанке в начале этой главы: нужны очень веские доказательства, чтобы убедить нас, что в целом надежный самолет разобьется. Нам необходимы очень веские доказательства, чтобы убедить нас, что Иисус Христос воскрес.

Прайс счел, что рассуждения Юма «противоречат разуму», что Юм неправильно понял Байеса. Он объяснял, что Юму следовало быть более точным, когда он говорит о θ – вероятности чуда. Даже те, кто верит в чудеса, не считают, что они происходят каждый день. Конкретизируем: представьте, что Прайс предложил Юму дать какую-то оценку частоте чудес, а тот говорит, что они случаются реже одного раза в 10 миллионов дней (27 400 лет), что дает θ > 99,99999 %. Предположим, Прайс верит, что 99,99999 % > θ > 99,999 %, то есть в то, что чудеса происходят реже, чем раз в 274 года, но чаще, чем раз в 27 400 лет. Теперь представьте, что 2000 лет подряд не происходило ни одного чуда. Вероятность того, что при таком условии прав Юм, составляет 7,04 %. Вероятность, что прав Прайс, – 92,89 %. Даже если за несколько тысячелетий не произошло ни одного чуда, это недостаточно надежно подтверждает, что чудес не существует. Просто за время жизни одного человека не набирается достаточного объема данных, чтобы подтвердить заявление Юма, будто чудес не существует.

Ричард Прайс направил «Десятку» на путь христианской морали. Он верил в воскресение Христа и использовал рациональные аргументы, чтобы поставить под сомнение само сомнение. Прайс полагал, что логическое мышление поможет обнаружить истины о мире, скрытые от нашего повседневного опыта. Бог был одной из этих истин.

Двумя тысячелетиями ранее в своей аллегории греческий философ Платон описал находящихся в пещере людей в оковах, которые смотрят на тени и способны видеть только смутные проекции истинного, более логичного мира снаружи. Аллегорию Платона часто используют для объяснения силы математики, и Прайс воспринимал ее очень серьезно. Он считал, что мы открываем новые истины, когда признаём, что тени на стене пещеры не реальны. Наш повседневный опыт – путаное представление о какой-то большей истине. Размышляя четче об истинной форме мира – посредством моделей, не зависящих от данных, – мы можем яснее рассуждать о путаных ситуациях, о тенях нашей повседневной жизни.

«Десятка», которую предвидел Прайс, формировалась из его религиозных убеждений и метафизики Платона. Он считал, что в математике есть мораль, что существует рациональный, правильный подход к жизни. Философ не только проповедовал такое представление, но и претворял его в жизнь. Он составил таблицы ожидаемой продолжительности жизни, которые почти целое столетие использовались для страховых выплат. Он считал свою работу способом защиты бедных людей от неопределенности: в ней показывалось, что почти все страховые компании того времени не способны выполнить свои будущие обязательства и должны совершенствовать свою политику. Прайс был ярым сторонником американской революции и близким другом Бенджамина Франклина; он полагал, что в Америке есть возможность создать систему, основанную на принципах свободы, где землей владели бы на равных, а политическая власть справедливо распределялась среди всех людей. Согласно видению Ричарда Прайса, США должны были стать страной, где религиозная рациональная «Десятка» могла бы в итоге процветать.

Современные практики «Десятки» редко говорят о морали, меньшинство из них верят в христианского Бога, однако многие унаследовали ценности Прайса: статистик, тщательно вычисляющий взносы автострахования для вашего тестя или свекра; государственный чиновник, планирующий наши пенсии или устанавливающий процентные ставки; научный сотрудник аппарата ООН, описывающий цели развития; климатолог, измеряющий вероятность различных повышений температуры на следующие двадцать лет; врач, балансирующий между рисками и стоимостью лечения. Все они используют байесовские рассуждения, чтобы создать более цивилизованное, справедливое и лучше организованное общество. Они помогают нам делиться рисками и неопределенностями с другими – и в результате, когда с одним из нас происходит ужасное, но редкое событие, расходы покрывают другие люди.

Уравнение суждений помогает участникам общества действовать на благо всех. Правильные суждения, если смотреть глазами Прайса, требуют, чтобы все мы прощали других и были к ним внимательны. Оно говорит нам, что не стоит отказываться от чудес. Он предполагает, что как минимум одно из десяти уравнений ставит нас на путь праведности.

Аудитория затихла, ожидая начала мероприятия. Бьорн нервничает. Последние пять лет жизни он посвятил благородному делу открытия новых истин – научным исследованиям. Я был руководителем, направлявшим его к цели. Сейчас он стоит перед коллегами, комиссией, своей семьей и друзьями и собирается защищать свою диссертацию. Бьорна нервирует сочетание этой разнородной аудитории и сложной темы его работы. Одна из глав диссертации называется «Прошлая ночь в Швеции» и представляет собой исследование связей между насильственными преступлениями и иммиграцией у него на родине. В другой главе он рассматривает, как «Шведские демократы» (популистская антииммиграционная партия) приобрели за последние десять лет известность в стране, знаменитой своей либеральной и социалистической политикой.

Для математиков из комиссии, сидящих в зале, это диссертация о статистических методах. Для второго научного руководителя, Ранжулы Бали Свайн, профессора экономики, которая работает в разных областях – от устойчивого развития до исследования того, как микрофинансирование помогает женщинам выбраться из бедности, – диссертация Бьорна нацелена на объяснение того, что происходит из-за смешения культур во всем мире. Семья Бьорна, Бломквисты, и его друзья хотят знать, что он выяснил об изменениях в Швеции. Их страна из однородной земли викингов превращается в мультикультурный плавильный котел из афганцев, эритрейцев, сирийцев, югославов и приехавшего британца.

Бьорн боится упасть с каната, на котором должен балансировать, чтобы осчастливить всех. Защита диссертации в Швеции начинается с выступления оппонента – человека, который должен прочитать работу, обсудить ее с кандидатом и представить исторический контекст в исследуемой области. Оппонент Бьорна – Иэн Вернон из Даремского университета.

Иэн рассказывает нам о принципах байесовского мышления. Мои примеры в этой главе относились к одной модели или использовали один параметр, но обычно ученые имеют дело с несколькими конкурирующими гипотезами. Задача Иэна – рассмотреть все эти альтернативные модели и присвоить им какие-то вероятности. Ни одна гипотеза не верна на 100 %, но по мере накопления свидетельств одни становятся правдоподобнее других. Он демонстрирует разные примеры, начиная с поиска нефтяных месторождений. Нефтедобывающие компании используют алгоритм, запатентованный Иэном и его коллегами, для поиска месторождений, которые дают наилучшие долговременные перспективы. Затем он переходит к здравоохранению. Когда исследователи планируют действия против малярии или ВИЧ, они сначала проводят математическое моделирование для прогнозирования результатов своих действий. Фонд Билла и Мелинды Гейтс использует методы Иэна для планирования своих программ по искоренению заболеваний.

Наконец Иэн переходит к одному из самых масштабных вопросов. Что происходило на первых стадиях существования Вселенной? Как впервые после Большого взрыва образовались галактики и какие модели объясняют размер и форму тех из них, что мы наблюдаем сегодня? Иэн смог уменьшить количество возможных моделей ранней Вселенной, найдя вероятные значения для семнадцати различных параметров, определяющих, как галактики расширяются в космическом пространстве. Презентация Иэна идеально ложится на аудиторию, демонстрируя мощь математических методов и широчайший спектр приложений. Семья и друзья Бьорна ахают, когда видят моделирование вращения и столкновения галактик, возможную модель начального этапа эволюции нашей Вселенной, параметры для которой были восстановлены с помощью формулы преподобного Байеса.

Приходит очередь Бьорна представить свою работу. Введение в масштабах Вселенной могло легко ошеломить и без того нервничающего аспиранта. Возможно, Бьорн обеспокоен сравнением его исследования всего одной страны в Скандинавии с огромным масштабом работ Иэна. Однако когда я смотрю на своего ученика, то вижу, что он спокоен и готов. А когда оглядываюсь на аудиторию, вижу гордость на их лицах. Бломквисты думают: вот что можно сделать с помощью математики, которую изучал Бьорн. Вот чем овладел их Бьорн: математикой Вселенной.

Социальные изменения так же сложны, как происхождение Вселенной, хотя и совершенно иначе. Бьорн показывает, как рост «Шведских демократов» можно объяснить преимущественно географическим положением. Эту партию поддерживают определенные регионы страны, особенно в самой южной области Сконе; однако поддержка есть и в центральной Даларне. Как ни странно, это не районы с самым высоким процентом иммигрантов. Возмущение появляется не потому, что в какую-то область приезжают иммигранты. Скорее, растет поддержка антииммиграционной политики в сельских областях – особенно там, где у людей низкий уровень образования.

После окончания презентации Иэн и комиссия задают Бьорну вопросы. Иэн и другие математики желают знать технические детали того, как Бьорн сравнивал модели и данные. Экономистка Линь Лерпольд, коллега Ранжулы и член комиссии, указывает на некоторые важные ограничения этого исследования. Бьорн не до конца разобрался в причинах антииммиграционных настроений. Он изучил закономерности изменений в местных сообществах, но не понял мышление их представителей. Чтобы ответить на вопросы Линь, нужны подробные беседы и анкеты.

Расспросы комиссии были дотошными, но справедливыми, а решение единогласным. Бьорн защитил диссертацию. Он присоединился к спецназу байесовских ученых.

Байесовское мышление изменило принципы науки в последние десятилетия. Оно идеально соответствует научному взгляду на мир. Экспериментаторы собирают данные (Д), а теоретики разрабатывают гипотезы или модели (М). Формула Байеса объединяет оба эти компонента.

Рассмотрим следующую научную гипотезу: использование мобильного телефона плохо влияет на психическое здоровье подростков. В моей семье этот вопрос горячо обсуждается – два подростка (и, если честно, два взрослых) целый день приклеены к экранам. В годы моей юности родители беспокоились, где я и чем занимаюсь. У нас с женой другие проблемы: дети слишком много времени проводят дома, уставившись в телефоны. Чего бы мы только не отдали за старые добрые разборки «Почему не пришел домой вовремя», «С кем встречалась?»…

Доктор Кристина Картер, социолог и автор нескольких книг о воспитании детей и производительности, категорически против чрезмерного использования мобильных телефонов, говоря, что «время за экраном – вероятная причина волны депрессии, тревог и суицида среди подростков». Ее статья в журнале Greater Good Magazine, выпускающемся в Калифорнийском университете в Беркли, излагает аргументы в два этапа. Во-первых, Картер ссылается на опрос родителей, почти половина которых считают, что их дети-тинейджеры зависимы от своих мобильных устройств, и 50 % озабочены, что это негативно скажется на их психическом здоровье. Во-вторых, она ссылается на данные, полученные при исследовании 120 115 подростков в Великобритании, которые отвечали на 14 вопросов о том, как они чувствуют себя с точки зрения счастья и удовлетворенности жизнью, и об их социальной жизни. Это исследование показало, что при превышении порога в один час в день дети отличались пониженным психическим благополучием, что измерялось с помощью опросника. Иными словами, чем больше дети используют свои телефоны, тем они несчастнее.

Звучит весомо, не так ли? Должен признаться, когда я прочитал эту статью в первый раз, она меня убедила. Написана специалистом со степенью, опубликована в рецензируемом журнале, который связан с университетом с мировым именем, в статье есть данные качественно проведенного опроса, поддерживающие точку зрения автора. Но есть одна проблема, и серьезная.

Кристина Картер заполнила только верхнюю часть уравнения суждений. Ее первый шаг – описание родительских страхов – аналогичен вероятности модели P{M}: это вероятность того, что родители верят, будто время у экрана влияет на психическое состояние детей. Ее второй шаг – демонстрация, что имеющиеся данные согласуются с гипотезой встревоженных родителей, то есть рассматривается величина P{Д|M}, и она действительно оказывается большой. Но Картер не учла того, что другие модели тоже могли бы объяснить проблемы подростков. Она определила числитель дроби в уравнении 2, но пренебрегла знаменателем. Доктор не сообщает нам P{Д|M–} для альтернативных гипотез, и мы не знаем P{M|Д} – вероятность того, что мобильный телефон объясняет подростковую депрессию, то есть именно то, что мы хотим знать.

Кэндис Оджерс, профессор психологии из Калифорнийского университета в Ирвайне, заполнила пробелы, оставленные Картер. В комментарии, опубликованном в журнале Nature, она пришла к совершенно другому заключению. Она начинает свою статью с признания проблемы. В США доля девочек в возрасте от 12 до 17, сообщавших о случаях депрессии, за период с 2005 по 2014 год выросла с 13,3 до 17,3 %; у мальчиков того же возраста тоже наблюдался рост, хотя несколько меньший. Нет сомнений, что использование мобильных телефонов за этот период увеличилось, здесь нам не нужны статистические данные. Оджерс также не оспаривает данные по британским подросткам, на которые ссылается Кристина Картер и которые указывают на рост случаев депрессии у тех, кто активно пользуется телефоном.

Однако Оджерс указывает, что депрессию у тинейджеров можно объяснить и другими причинами. Например, и отсутствие регулярного завтрака, и сон в разное время оказались втрое более важными факторами для прогнозирования психического состояния подростков, чем пользование телефонами. На языке теоремы Байеса завтрак и сон – альтернативные гипотезы, которые могут объяснить депрессию, и для них вероятность P{Д|M–} велика. Если их учесть в знаменателе формулы Байеса, это перевесит числитель, и искомая вероятность P{M|Д} того, что пользование мобильными телефонами связано с депрессией, становится меньше – не пренебрежимо малой, но достаточно маленькой, чтобы не считать ее важным фактором при объяснении психического здоровья подростков.

Более того, есть документально подтвержденная польза телефонов для тинейджеров. Во многих работах показано, что дети используют гаджеты, чтобы поддерживать друг друга и создавать долговременные социальные структуры. У большинства ребят среднего класса – группы, на которую ориентируются советчики по поводу экранного времени, – мобильные телефоны улучшают способность заводить настоящие, прочные дружеские отношения; и не только в интернете, но и в реальной жизни. Как говорит Кэндис Оджерс в своей статье, с проблемами сталкиваются дети из неблагополучных семей. Менее благополучные подростки скорее начнут драться из-за того, что происходило в соцсетях. Те, кого травили в жизни, позже с большей вероятностью станут жертвами и в интернете.

Мои дети общаются с детьми по всему миру и часто узнают в Сети что-то новое. Я слышал, как на прошлой неделе Элиза и Генри обсуждали барабаны бонго и культурную апроприацию.

Элиза сказала:

– Это базовое уважение: если кто-то говорит, что его оскорбляет исполнение вами музыки его культуры, то лучше остановиться.

– Тогда Эминем – это культурная апроприация? – возразил Генри.

Я точно не мог вести такие разговоры с сестрой, когда нам было тринадцать и пятнадцать. Я не уверен даже, что мы могли бы вести их сейчас. Дети, рожденные в 2000-х, имеют доступ к важным идеям и информации, которые находились вне рамок восприятия тех, кто рос в 1970-е, 1980-е и даже 1990-е.

Вернемся к Эми и Рэйчел, поскольку я пропустил кое-что важное.

Числа, которые я использовал в том примере (один человек из 20 стервозный; эти люди тратят на гадости половину времени; даже хорошие люди ведут себя так один день из десяти), не просто произвольны, но и субъективны – свои для каждого человека. В зависимости от вашего жизненного опыта вы будете доверять людям больше или меньше, чем Эми. Это как с авиакатастрофами: ужасная и объективная реальность. Выбор Эми, как смотреть на новых соучеников, или мой способ классифицировать коллег, полностью основан на нашем субъективном опыте общения с людьми, которых мы встречали ранее. Нет никаких объективных способов измерить «стервозность», «сучность» или «козлиность».

Да, числа в истории Эми субъективны. Однако дело вот в чем. Формула Байеса работает не только с объективными вероятностями, но и с субъективными. Она дает нам возможность рассуждать о числах, даже если они не абсолютно точные. Мы можем поменять их и получить другие результаты, но нельзя изменить логику, которую нам рекомендует байесовский подход.

Сделанные предположения называются априорными. В уравнении 2 P{M} – априорная вероятность того, что наша модель верна. Часто такие вероятности можно получить из субъективного опыта. Но не может быть субъективной P{M|Д}, вероятность истинности нашей модели после того, как мы увидели какие-то данные. Пересчет вероятностей должен производиться с помощью формулы Байеса.

Многие полагают, что математика обязательно имеет дело с объективными вещами. Это не так. Это способ представления мира и рассуждений о нем; и иногда то, о чем мы спорим, известно только нам. В конце концов, никто другой, возможно, никогда не узнает, считает Эми Рэйчел стервой или нет. Этот процесс может быть навсегда сокрыт в ее мозге.

Вспомните о моем кинематографическом представлении мира – фильмах, которые я проигрываю себе день за днем, порой очень личных. Это могут быть опасения по поводу того, что чувствует моя жена; мысли о будущем дочери; фантазии о том, как я веду мини-футбольную команду сына к победе в турнире; мечта о том, как в один прекрасный день я стану автором бестселлера. Мне не надо рассказывать вам о них, поскольку они принадлежат исключительно мне. Уравнение суждений не говорит нам, какие фильмы нужно иметь в коллекции или о чем мечтать. Оно просто говорит, как нужно рассуждать об этих мечтах, поскольку каждый из таких «фильмов» – модель мира. Уравнение суждений позволяет нам обновлять вероятности, которые мы связываем с каждой мечтой, но не говорит, какие мечты нужно иметь.

После защиты Бьорна Иэн Вернон за бокалом шампанского сказал мне: «Многие, даже математики и другие ученые, не осознают, что настоящая сила байесовского подхода в том, как он заставляет вас определить, что вы думали до эксперимента и после него. Байесовский анализ требует, чтобы вы разбили свои рассуждения на модели и по очереди искали свидетельства для них. Вы можете считать, что данные подтверждают ваше предположение, но нужно быть честным в отношении того, насколько сильно вы поддерживали свою гипотезу до этого эксперимента».

Я согласился. Иэн говорил в целом, думая при этом о защите Бьорна и использовании байесовской теории для объяснения подъема крайне правых сил в шведской политике. В этом проекте я проработал с Бьорном все детали, изучив факторы, которые заставляют людей голосовать за националистические партии. Теперь пытался применить тот же подход к вопросу из собственной семейной жизни. Я не специалист по психическому здоровью или мобильным телефонам, но уравнение суждений дает мне способ интерпретировать результаты, полученные другими, – способ оценить относительную ценность аргументов, выдвинутых учеными. Я использовал теорему Байеса, чтобы проверить, соблюдали ли они критерии для правильного суждения. Посмотрели ли они на собственную и альтернативную модель мира? Кэндис Оджерс представила в своих рассуждениях все стороны; Кристина Картер – только одну.

Иногда я крайне разочарован, когда вижу, как некритично воспринимают люди советы так называемых экспертов по воспитанию, образу жизни или здоровью. Как неопытные игроки, которые просят у меня совета только о предстоящем серьезном матче, так и потребители таких советов смотрят не дальше последнего исследования. Они не понимают, что обеспечение здорового и сбалансированного образа жизни требует долгосрочной позиции, как успешная азартная игра – долгосрочной стратегии.

Но не только Кристина Картер ответственна за представление всех аспектов рассматриваемого вопроса. Вам может показаться странной такая моя позиция, поскольку я счел ее работу вводящей в заблуждение; но я также понимаю, что она отражает беспокойство многих родителей, включая меня. Данные, описанные ею, реальны, и она считает, что они подтверждают ее модель. Описывать поддержку альтернативных моделей не совсем ее дело.

Проверять достоверность ее модели – большей частью наше дело. Когда я читаю авторские колонки, то стараюсь убедиться, что их создатели – независимо от квалификации – разобрались во всех частях нашего уравнения. Мне как родителю оказалось нетрудно получить более полное представление о роли экранов в нашей жизни. Все статьи, что я использовал, есть в свободном доступе в интернете; и мне понадобилось несколько вечеров собственного времени у экрана, чтобы скачать и прочитать их. Как только разобрался в вопросе, обсудил результаты с детьми. Я сказал им, что и хороший сон, и правильный завтрак втрое важнее для их психического состояния, чем время в телефонах. Я рассказал, что телефоны отчасти полезны, подчеркнув: это вовсе не подразумевает, что они должны проводить все вечера на диване за просмотром YouTube. Физические нагрузки и социальное общение необходимы, и уж точно не стоит брать телефоны в спальню. Мне кажется, Элиза и Генри всё поняли.

Можно услышать, как те же люди, которые некритично потребляют информацию о воспитании детей, выражают скептицизм, когда слышат более сбалансированную точку зрения от ученых, подобных Кэндису Оджерсу. Когда ученые излагают все стороны проблемы, такие люди считают, что это говорит о неуверенности специалистов. В научном сообществе активно обсуждаются такие темы, как изменение климата, достоинства разных диет или причины преступности. Но обсуждения и сравнение всех возможных гипотез вовсе не признак слабости или нерешительности участников дискуссии. Скорее, это признак силы и основательности. Это знак преимущества, того, что вы рассмотрели все возможности.

В мире полно людей, дающих советы. Как быть организованными на работе и дома. Как оставаться спокойными и сосредоточенными. Как стать лучше. Выберите идеальную работу. Идеального партнера. Идеальную жизнь. Десять главных вещей, которые нужно сразу сделать на новой работе. Десять вещей, которых нужно избегать. Десять главных уравнений.

Спокойствие, как у йогов. Самоосознание. Глубокое мышление и медленное дыхание. Тигры. Кошки и собаки. Популярная психология и эволюционное поведение. Будьте пещерным человеком, охотником-собирателем или греческим философом. Отключитесь. Подсоединитесь. Расслабьтесь. Зарядитесь. Выпрямитесь и никогда не лгите. Плюйте на всё, и вы всегда будете счастливы. Не откладывайте, делайте сейчас, и быстрее.

Всем таким советам не хватает структуризации. Важная информация перемешана с мнениями и ерундой. Уравнение суждений позволяет организовывать и оценивать. Оно превращает любой совет, желательный или нежелательный, в модель, которую можно проверить, используя данные. Внимательно прислушивайтесь к мнению других, записывайте альтернативы, собирайте данные и выносите суждение. Корректируйте свое мнение по мере медленного накопления свидетельств за и против той или иной идеи. С помощью того же процесса судите о действиях других. Всегда давайте им второй и даже третий шанс – гарантируя, что ваши решения определяются фактами, а не эмоциями. Используя формулу Байеса, вы не только будете делать оптимальный выбор, но и обнаружите, что завоюете доверие других. Вы прославитесь своими здравыми суждениями.