Глава 9. Уравнение обучения

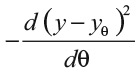
Вероятно, вы слышали, что в технологиях будущего станет доминировать искусственный интеллект (ИИ). Ученые уже натренировали компьютеры побеждать в го, а сейчас испытывают беспилотные автомобили. Да, я объясняю некоторое количество уравнений в этой книге, но не забыл ли я что-нибудь? Не стоит ли мне также рассказать вам секреты, стоящие за ИИ, который используют Google и Facebook? Не следует ли мне объяснить, каким образом мы можем заставить компьютеры учиться так же, как мы сами?

Я открою вам секрет, который не совсем соответствует содержанию фильмов «Она» или «Из машины». Он также не увязывается с опасениями Стивена Хокинга или шумихой Илона Маска. Тони Старк, вымышленный супергерой – Железный человек из комиксов Marvel, – не обрадовался бы тому, что я скажу: искусственный интеллект в его современной форме не больше (и не меньше) чем десять уравнений, которые инженеры используют совместно и творчески. Но прежде чем я объясню, как работает ИИ, сделаем рекламную паузу.

Примерно во времена песни Gangnam Style у YouTube возникла одна проблема. Шел 2012 год; хотя сотни миллионов людей щелкали по видеороликам и посещали этот сайт, они не оставались там надолго. Новые ролики вроде «Чарли укусил меня за палец», «Двойная радуга», «Что говорит эта лиса?» или Ice Bucket Challenge удерживали их внимание всего на тридцать секунд, а дальше они снова возвращались к телевизору или к другим занятиям. Чтобы получать доход от рекламы, YouTube должен был стать местом, где пользователи будут зависать.

Значительную часть проблемы представлял алгоритм сайта. Он использовал систему рекомендации видео, основанную на уравнении рекламы из . Для роликов, которые смотрели и отмечали лайками пользователи, строилась корреляционная матрица. Однако этот метод не учитывал, что молодежь хотела смотреть самые свежие видео, и не уточнял, насколько интересен пользователям ролик. Он просто показывал видео, которые смотрели другие. В результате в списках рекомендуемых продолжала появляться норвежская армия, исполняющая Harlem Shake, а пользователи с сайта уходили.

Владельцы YouTube обратились к специалистам Google: «Эй, Google, как помочь детям найти те видеоролики, которые им нравятся?» – спросили (наверное) они. Три разработчика, получившие эту задачу, – Пол Ковингтон, Джей Адамс и Эмре Саргин – вскоре поняли, что самый важный критерий для оптимизации YouTube – время просмотра. Если бы сайт мог заставить пользователей смотреть как можно больше роликов как можно дольше, то легче было бы вставлять рекламу через регулярные промежутки времени и зарабатывать больше денег. При этом короткие свежие ролики были не так важны, как целые каналы, обеспечивающие постоянное появление свежего и длительного контента. Задача состояла в том, чтобы найти способ выявить этот контент на платформе, где каждую секунду загружаются часы видеороликов.

Ответ разработчиков имел форму воронки. Это приложение брало сотни миллионов видеороликов и сводило их примерно к десятку рекомендаций, представленных сбоку на странице сайта. Каждый пользователь получал собственную персонифицированную воронку с роликами, которые, возможно, он захочет посмотреть.

«Воронка» – нейронная сеть, которая изучает наши предпочтения при просмотре. Такие сети лучше всего представлять в виде столбца входных нейронов слева и выходных справа. Между ними находятся слои соединительных нейронов, известных как скрытые (см. ). В сети могут быть десятки или даже сотни тысяч нейронов. Она не реальна в физическом смысле: это компьютерные коды, которые моделируют взаимодействие нейронов. Однако аналогия с мозгом полезна, потому что именно прочность связей между нейронами позволяет их сетям изучать наши предпочтения.

Каждый нейрон кодирует определенные аспекты того, как сеть реагирует на входные данные. В «Воронке» нейроны фиксируют взаимосвязи между разными элементами контента и каналов YouTube. Например, люди, которые смотрят правого комментатора Бена Шапиро, также склонны смотреть и видео Джордана Питерсона. Я знаю это, потому что после завершения своего исследования для об уравнении уверенности YouTube с маниакальным упорством подсовывает мне ролики Шапиро. Где-то внутри «Воронки» есть нейрон, который представляет связь между этими двумя иконками «Темной сети интеллектуалов». Когда он получает входной сигнал, что я заинтересовался роликом Питерсона, то дает на выходе вывод, что меня могут интересовать и ролики Шапиро.

Мы можем понять, как «обучаются» искусственные нейроны, узнав, как формируются связи внутри сети. Нейроны кодируют отношения в виде параметров – регулируемых величин, которые измеряют прочность отношений. Рассмотрим нейрон, отвечающий за определение того, сколько пользователей будут тратить время на просмотр выступления Бена Шапиро. Внутри этого нейрона имеется параметр θ, который соотносит время, потраченное на видео Шапиро, с количеством просмотренных роликов с Джорданом Питерсоном. Например, мы можем спрогнозировать, что количество минут, которое пользователь тратит на видео Шапиро (обозначим его y_θ), равно θ, умноженному на количество просмотренных роликов Питерсона. Скажем, если θ = 0,2, то прогнозируется, что человек, просмотревший десять роликов Питерсона, потратит y_θ = 0,2 ∙ 10 = 2 минуты на видео Шапиро. Если θ = 2, то прогнозируется, что тот же человек потратит y_θ = 2 ∙ 10 = 20 минут на Шапиро, и т. д. Процесс обучения включает корректировку параметра θ для улучшения прогнозов для времени просмотра.

Предположим, первоначальное значение нейрона θ = 0,2. Здесь появляюсь я, который видел 10 выступлений Питерсона и трачу на просмотр Шапиро y = 5 минут. Квадрат разности между прогнозом (y_θ) и реальностью (y) составляет:

Мы уже видели идею квадрата разности – в , когда измеряли стандартное отклонение. Вычислив (y – y_θ)², получаем меру того, насколько хороши (или плохи) прогнозы нейронной сети. Расхождение между прогнозом и реальностью равно 9, так что, похоже, предсказание не особо хорошее.

Чтобы чему-то научиться, искусственный нейрон должен знать, что он делал неправильно, когда прогнозировал, что я буду смотреть только две минуты. Поскольку прочностью связи между количеством видеороликов Питерсона и типичным временем, которое пользователь тратит на просмотр Шапиро, управляет параметр θ, его увеличение также увеличит и предсказанное время y_θ. Поэтому, например, если мы возьмем для θ небольшое увеличение dθ = 0,1, то получим y_θ+dθ = (θ + dθ) ∙ 10 = (0,2 + 0,1) ∙ 10 = 3 минуты. Такой прогноз будет ближе к реальности:

Именно это улучшение и использует уравнение 9 – уравнение обучения.

Это выражение говорит, что мы рассматриваем, как маленькое изменение dθ увеличивает или уменьшает квадрат расстояния (y – y_θ+dθ)². Конкретно в нашем примере получаем:

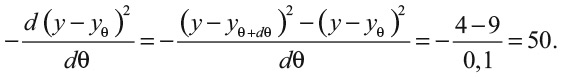
Поскольку эта величина положительна, увеличение θ улучшает качество прогноза – и расстояние между ним и реальностью уменьшается.

Математическая величина, задаваемая уравнением 9, известна как производная по θ или градиент. Она измеряет, приближает или отдаляет ли нас изменение θ от хорошего прогноза. Процесс медленной корректировки θ на основании производной часто называют градиентным подъемом, что вызывает в мозге образ человека, движущегося по крутому уклону холма. Следуя по градиенту, мы можем медленно улучшать точность искусственного нейрона (см. рис. 9).

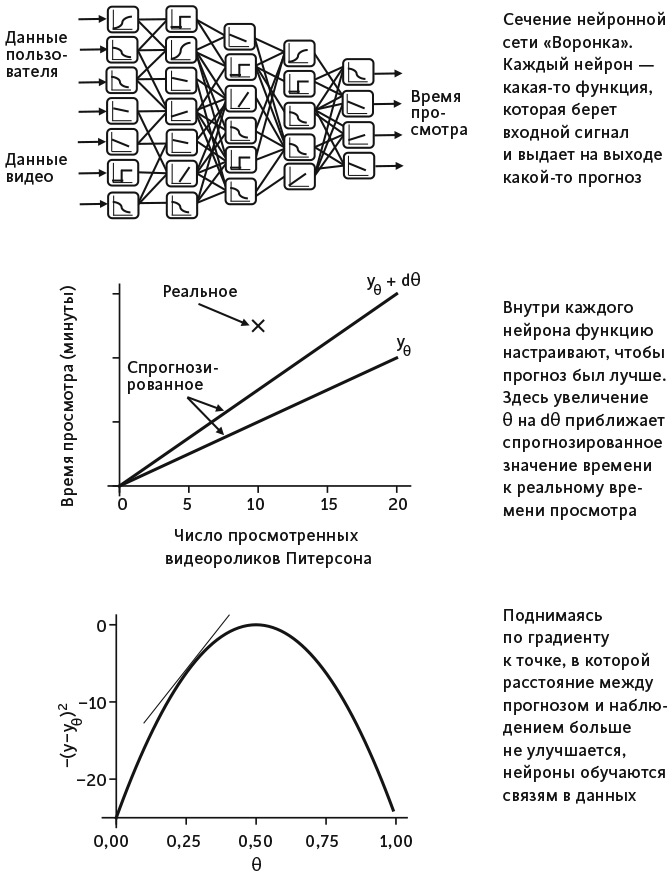
Рис. 9. Как обучается нейронная сеть

«Воронка» работает не только с одним нейроном, а сразу со всеми. Первоначально все параметры принимают случайные значения, и нейронная сеть делает очень плохие прогнозы о времени, которое люди потратят на просмотр видео. Затем инженеры начинают подавать на входные нейроны (широкий конец «Воронки») данные о просмотре роликов пользователями YouTube. Небольшое число выходных нейронов (узкий конец «Воронки») измеряет, насколько хорошо нейронная сеть предсказывает продолжительность просмотра роликов. Сначала ошибки в прогнозах очень велики. При применении метода обратного распространения ошибки отклонения, измеренные на узком конце, передаются обратно по слоям «Воронки». Каждый нейрон измеряет градиент и улучшает параметры. Медленно, но верно нейроны поднимаются по градиенту, и прогнозы постепенно улучшаются. Чем больше данных от пользователя YouTube подается в сеть, тем лучше будет прогноз.

Нейрон из моего примера, занимающийся отношением Шапиро/Питерсон, не нужно изначально кодировать в сети. Сила нейронных сетей в том, что нам не нужно сообщать им, какие отношения искать в данных: сеть сама находит эти взаимоотношения в процессе градиентного подъема. Поскольку связь Шапиро/Питерсон прогнозирует время просмотра, в итоге один или несколько нейронов начнут использовать эту связь. Они будут тесно взаимодействовать с другими нейронами, связанными с другими авторитетами «Темной сети интеллектуалов» и даже с более правыми идеологиями. Это создает статистически корректное представление типа человека, который, вероятно, смотрит видеоролики Джордана Питерсона.

Уравнение 9 – основа методов, известных как машинное обучение. Постепенное улучшение параметров с помощью градиентного подъема можно рассматривать как процесс «обучения»: нейронная сеть («машина») постепенно «учится» делать всё лучшие прогнозы. Если предоставить ей достаточно данных (а у YouTube их навалом), нейронная сеть изучает закономерности внутри этих данных. Как только она «обучилась», «Воронка» может спрогнозировать, сколько времени пользователь YouTube проведет за просмотром видеороликов. Платформа воплотила эту методику в жизнь. Она берет видеоролики с самым большим прогнозируемым временем просмотра и ставит их в рекомендательные списки для пользователей. Если человек не выбрал новое видео, YouTube автоматически воспроизводит тот ролик, который, по его мнению, понравится пользователю больше всего.

Успех «Воронки» был ошеломительным. В 2015 году время, потраченное на просмотр в YouTube пользователями в возрасте от 18 до 49 лет, возросло на 74 %. К 2019 году число просмотров выросло в 20 раз по сравнению с моментом, когда специалисты Google начали свой проект, причем 70 % из них берутся из рекомендованных видео. Дуг Коэн, специалист по данным из Snapchat, был восхищен этим решением. «Google решил за нас проблему разведки и эксплуатации», – сказал он мне. Вместо того чтобы бродить по разным сайтам и пытаться найти лучшие видео или ждать, пока вам кто-нибудь пришлет интересную ссылку, теперь вы можете часами сидеть в YouTube, выбирая либо «Следующее» видео, либо один из десятка предлагаемых альтернативных вариантов.

Если вы считаете, что ведете на YouTube разведку по своим интересам, а обнаруживаете, что смотрите предлагаемые видеоролики, то, к сожалению, заблуждаетесь. «Воронка» превратила YouTube в подобие телевидения, только программу составляет искусственный интеллект. И многие приклеиваются к этому экрану.

Ной хотел бы стать более популярным в Instagram. У многих его друзей подписчиков (фолловеров) больше, чем у него, и он с завистью смотрит, как им летят лайки и комментарии. Ной смотрит на аккаунт своего друга Логана: около 1000 подписчиков, на каждый пост сотни лайков. Он хочет быть похожим на Логана и ставит себе цель: y = 1000 подписчиков. При текущей стратегии у него y_θ = 137. До нужного числа далеко.

В течение следующей недели Ной постепенно начинает размещать все больше постов. Он полагает, что чем больше публикаций, тем больше людей на него подпишутся, и вывешивает фотографии своего ужина, новых туфель или прогулки до школы, но не старается улучшить качество снимков. Ной просто фотографирует все, что видит, и выкладывает это в блоге. В терминах уравнения 9 параметр θ, который он регулирует, – отношение количества его сообщений к качеству. Ной увеличивает количество постов, поэтому dθ > 0.

Отзывы неблагоприятные. «Зачем ты спамишь?» – пишет под одной из фотографий его подруга Эмма, добавляя к тексту озадаченный смайлик. Некоторые знакомые Ноя отписались от него. Его популярность упала: y_θ+dθ = 123, то есть произошло снижение на 14 человек. Расстояние до цели увеличилось. Он опустился по градиенту, а не поднялся. В последующие месяцы Ной снижает количество публикаций и сосредоточивается на качестве. Несколько раз в неделю он делает фотографию какого-нибудь приятеля с мороженым или забавный снимок своей собаки, тщательно редактирует эти фотографии и с помощью фильтров добивается, чтобы его друзья выглядели хорошо. И во время такого перехода от количества к качеству Ной еще и измеряет y_θ. Количество его подписчиков медленно, но уверенно увеличивается. Через шесть месяцев оно выросло до 371, но потом застыло, седьмой месяц не дал прибавки.

Так мы приходим к важному уроку из уравнения 9: Ною нужно расслабиться и перестать стремиться к цели в 1000 фолловеров. Хотя (y – y_θ)² = (1000 – 371)² = 395 641 – по-прежнему большое число, выражение в уравнении 9 больше не меняется:

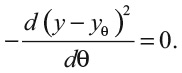
Уравнение говорит, что Ною надо остановиться в своей стратегии работы с социальной сетью и довольствоваться тем, что он получил. Больше нет надобности сравнивать себя с Логаном: Ной достиг своего пика популярности.

Применяя уравнение 9, мы должны помнить об итоговой цели, но в первую очередь нужно руководствоваться тем, движемся мы вверх или нет. Как гласит мудрость, если вы забрались на вершину горы, наслаждайтесь видом. Математика подтверждает это.

Разница между оптимизацией, которую создают алгоритмы машинного обучения вроде «Воронки», и оптимизацией Ноя в том, что он пытался увеличить число подписчиков, а машинное обучение стремится оптимизировать точность прогнозов. В случае «Воронки» y_θ – это прогнозы, как долго пользователи будут смотреть видео, а y – реальная продолжительность просмотра. YouTube хотел бы уметь предсказывать предпочтения пользователей с максимально возможной точностью, но понимает, что его прогнозы никогда не будут идеальными. «Воронка» удовлетворена, когда осознаёт, что лучшего добиться не может.

Фокус в использовании уравнения обучения в том, чтобы честно говорить, как ваши действия увеличивают или уменьшают разницу между целью и реальностью. Некоторые могут обвинить Ноя в том, что в своих попытках оптимизировать влияние в соцсети он «поверхностен» или что-то «фальсифицирует». Я не согласен. Работа с такими влиятельными специалистами, как Кристиан Ихо, который ведет в соцсети блог об уличной моде, научила меня обратному. Кристиан использует аналитические инструменты Google, чтобы изучать, как отношение количества к качеству в публикациях создает поток пользователей; однако все равно понимает, что его данные относятся к людям. Когда семнадцатилетний подросток сделал селфи в дизайнерской футболке, лицо Кристиана засветилось. Он поставил лайк и написал комментарий: «Отлично смотрится!» Он не шутил. Нет противоречия между тем, чтобы изучать данные и быть на 100 % искренним в том, кто вы и что делаете.

При аккуратном применении уравнение обучения помогает вам оптимизировать собственную жизнь. Пытаетесь ли вы добиться успеха в соцсетях или готовиться к экзамену, вы всегда стремитесь постепенно подниматься по градиенту. Ставьте себе цель, но не фокусируйтесь на расстоянии до нее. Пусть вас не беспокоят люди, которые популярнее вас, или ровесники с более высокими оценками. Сосредоточивайтесь на ежедневных шагах. Сфокусируйтесь на градиенте: на дружбе, которую приобретаете, или на новых знаниях, полученных в процессе учебы. Если вы видите отсутствие прогресса, признайтесь себе в этом. Вы добрались до вершины холма, и теперь пора понаслаждаться видом. Однако имейте в виду, что следовать градиенту не всегда идеальное решение; иногда вы попадете в ловушку неоптимального решения. Тогда нужно сбросить настройки и начать заново. Найдите новую гору для подъема или новые параметры, которые можно регулировать.

В 2019 году Джарвис Джонсон бросил работу специалиста по программному обеспечению. Его ютьюб-канал, где он выкладывал ролики о своей жизни программиста, привлекал все больше подписчиков. Джонсон решил проверить, сможет ли стать полностью «интернетным человеком», как он теперь себя называет.

Чтобы стать ютьюбером, нужны две вещи: интересный контент и глубокое понимание процессов «Воронки». У Джарвиса есть и то и другое, а его ролики сочетают эти элементы с юмором. Он исследует, как некоторые каналы используют этот алгоритм ради своей выгоды, манипулируя «Воронкой» так, чтобы она выдавала рекомендации в их пользу. Затем излагает свои результаты в завлекательных интересных видео на этой же платформе.

Расследования Джарвиса сфокусировались на цифровой студии, которая называется TheSoul Publishing. Они именуют себя «одной из крупнейших медиакомпаний в мире» и заявляют, что их задача – «вовлекать, вдохновлять, развлекать и просвещать». Джарвис начал с просмотра одного из самых успешных каналов – 5-Minute Crafts. Там предлагаются лайфхаки – советы, которые облегчают повседневную жизнь. В одном из видео со 179 миллионами просмотров сайт утверждал, что несмываемый маркер можно удалить с футболки, если использовать смесь санитайзера для рук, разрыхлителя для теста, лимонного сока и зубную щетку. Джарвис решил проверить это сам, написав текст на белой футболке и последовав инструкциям. Результат? После выполнения всех инструкций и машинной стирки текст остался виден. Джарвис проверял совет за советом – и оказывалось, что они либо тривиальны, либо не работают. Лайфхаки канала 5-Minute Crafts были бесполезны.

Другой из каналов TheSoul – Actually Happened – утверждал, что показывает реальные истории из жизни подписчиков. Джарвис обнаружил, что контент создан «сценаристами», которые писали правдоподобные истории, рассчитанные на подростков из США, используя в качестве исходных материалов Reddit и другие социальные сети. Джарвис объяснил мне, что Actually Happened изначально копировал другой канал – Storybooth, который действительно воспроизводил подлинные истории детей и подростков. На платформе Storybooth дети часто делятся собственными историями, что помогает обеспечить искренность и честность.

«Алгоритм YouTube не может определить разницу между Storybooth и Actually Happened», – сказал мне Джарвис в беседе в мае 2019 года. Канал Actually Happened применяет те же названия, описания и теги, что и Storybooth, и ютьюбовская «Воронка» считает их примерно эквивалентными и начинает создавать ссылки между этими сайтами. «Actually Happened наводнили рынок историями. Они нанимали подрядчиков по цене ниже рыночной и выдавали по видео в день, – продолжал Джарвис. – Затем они достигли уровня, когда им больше не требовалось копировать Storybooth». Как только они добились миллиона подписчиков, «Воронка» решила, что дети хотят смотреть Actually Happened. Алгоритм признал это вершиной холма для своих пользователей.

Джарвис считал, что моральные проблемы вокруг каналов компании TheSoul запутанны. «Я, конечно, создавал контент, как у других, надеясь привлечь аудиторию, но я бы не мог делать это так явно и массово. Что не дает этой компании проделывать такое со всеми жанрами на платформе?»

Ограниченность алгоритма YouTube в том, что его не заботит контент, который он продвигает, или работа, затраченная на его создание. Я сам ощутил это, когда YouTube решил, будто меня интересует Бен Шапиро. Любой, кто сажал своих детей перед YouTube на час, наверняка замечал, как их затягивает в странный мир видеороликов с показом игрушек, вазочек с мороженым из цветного пластилина и диснеевских головоломок. Посмотрите на ролик PJ Masks Wrong Heads for Learning Colors: выглядит так, как будто на его создание ушло полчаса, но он имеет 200 миллионов просмотров. «Воронка» может рекомендовать не просто видеоролики плохого качества; они бывают негодными. В 2018 году журнал Wired зафиксировал видео, где собаки из мультсериала «Щенячий патруль» пытались совершить самоубийство, а Свинку Пеппу обманом заставили есть бекон. Одно из расследований The New York Times обнаружило, что YouTube рекомендовал семейные видео с голыми детьми, играющими в бассейнах-лягушатниках, своим пользователям, которые интересовались педофилией.

YouTube может дать нам «видение воронки». Возможно, его цель – обеспечение лучших рекомендаций для вас, однако уравнение 9 выполнено, когда обнаруживается наилучшее решение для доступных данных. Происходит подъем по градиенту обучения, пока не будет достигнут пик, а затем остановка – чтобы вы наслаждались видом, причем каким угодно. «Воронка» совершает ошибки, а ответственность за их исправление лежит на нас. YouTube не всегда преуспевал в решении этой задачи.

Некоторые люди со стороны могут решить, что участники «Десятки» похожи на Железного человека – Тони Старка (промышленники и талантливые инженеры, использующие технологии для преобразования мира). Но если бы любому из участников «Десятки» предложили выбрать какого-нибудь супергероя, чтобы описать себя, это, вероятно, был бы Человек-паук (Питер Паркер). У него нет плана, нет нравственной программы – он как подросток, пытающийся сохранить контроль над организмом, когда тот меняется неожиданно.

Напряженность среди участников «Десятки» можно рассматривать по-разному. Похожи ли они на наивного Марка Цукерберга из фильма «Социальная сеть» или роботоподобного Марка Цукерберга, дающего свидетельские показания в юридическом и торговом комитетах Сената США? Похожи ли они на того Илона Маска, который курит травку на камеру, или на того, который связывает наше будущее с перелетом на Марс?

С одной стороны, уравнения дают «Десятке» возможность выносить безупречные суждения, и им доверяют планировать глобальные перемены в нашем обществе. Они создали научный подход, который укрепляет уверенность в моделях, использующих данные. Они связали нас всех так, как мы не ожидали. Они оптимизируют и улучшают работу. Они приносят эффективность и стабильность. С другой стороны, эти участники будут придерживаться уравнения вознаграждения, которое предлагает брать то, что есть сейчас, и забыть о прошлом. Они создают преимущество перед теми, кто не может позволить себе платить.

Это как раз то, о чем Алфред Джулс Айер говорил в 1936 году: в математике нет морали, а если и была когда-то, то сейчас уже утрачена. Невидимость «Десятки» означает, что мы не можем найти даже подходящую аналогию с супергероем. Кто такие участники «Десятки»? Наивные подростки, осознающие, как Питер Паркер, что с большой властью приходит и большая ответственность; или жадные до власти маньяки, которые хотят управлять миром «ради его же блага»? Может, они даже похожи на суперзлодея Таноса из вселенной Marvel, готового убить половину людей, – поскольку думают, что это станет оптимальным решением?

Что бы они ни думали о себе, нам нужно знать, что они замышляют, потому что, куда бы они ни отправились, они всё меняют.

Когда мы изучаем примеры современного ИИ – например, нейронную сеть компании DeepMind, которая стала лучшим в мире игроком в го, или искусственный интеллект, который научился играть в «Космических захватчиков» либо в другие игры для Atari, – мы должны считать их выдающимися достижениями инженерии. Некая группа математиков и программистов собрала воедино все фрагменты. За этим ИИ стоит не какое-то одно уравнение.

Но – и это важно для всего моего проекта по описанию десяти уравнений – компоненты искусственного интеллекта включают девять из них. Так что в финале я попробую объяснить, как DeepMind стала мастером игры, используя ту математику, которую мы уже изучили в этой книге.

Представьте сцену, где в окружении кольца столиков стоит шахматный гроссмейстер. Он подходит к одному столу, изучает позицию и делает ход. Затем переходит к следующему и делает ход там. В конце сеанса оказывается, что он выиграл все партии. Сначала может показаться невероятным, что гроссмейстер отслеживает столько шахматных партий одновременно. Неужели он может помнить, как развивалась игра до данного момента, и решать, что делать дальше? Но потом вы вспоминаете уравнение умений.

Ситуацию в партии можно увидеть непосредственно на доске: защитная структура пешек, качество убежища для короля, насколько хорош для атаки ферзь и т. д. Гроссмейстеру не нужно знать, как шла игра до настоящего момента, достаточно изучить позицию и выбрать следующий ход. Умения шахматиста можно измерить тем, как он берет текущее состояние доски и переводит его в новое, делая какой-то закономерный ход. Это новое состояние уменьшает или увеличивает его шансы на победу в партии? При оценке гроссмейстеров применяется .

«Многие игры с полной информацией – например, шахматы, шашки, реверси или го – можно считать марковскими». Такой была первая фраза в разделе «Методы» статьи Дэвида Сильвера и других специалистов Google DeepMind об их программе, ставшей лучшим игроком в го в мире. Это наблюдение упрощает задачу нахождения решения для этих игр, поскольку позволяет сосредоточиться на поиске оптимальной стратегии для текущего состояния на доске, не заботясь о том, что происходило до этого момента.

Мы уже анализировали математику отдельного нейрона в . Уравнение 1 брало текущие коэффициенты для какого-нибудь футбольного матча и преобразовывало в решение, стоит нам делать ставку или нет. По сути, это упрощенная модель того, что делает отдельный нейрон в вашем мозге. Он получает внешние сигналы – от других нейронов или из внешнего мира – и преобразует их в решение, что ему сделать. Такое упрощающее предположение легло в основу первых моделей нейронных сетей, а уравнение 1 использовалось для моделирования реакции нейронов. Сегодня это одно из двух очень похожих уравнений, которые используются для моделирования нейронов почти во всех сетях.

Далее мы обратимся к одному из вариантов уравнения вознаграждения. В уравнении 8 величина Q_t была оценкой качества сериала Netflix или вознаграждения, получаемого от проверки аккаунта в Twitter. Вместо того чтобы оценивать один фильм или один аккаунт, сейчас мы просим нашу нейронную сеть оценить 1,7 × 10¹⁷² разных состояний в игре го или 10¹⁷² сочетаний клипов и пользователей на YouTube. Обозначим Q_t(s_t, a_t) качество состояния мира s_t при условии, что мы намереваемся произвести некоторое воздействие a_t. В игре го состояние s_t – решетка 19 × 19, где у каждого узла (в го они называются пунктами) есть три возможных состояния: пуст, занят белым камнем или занят черным камнем. Возможные действия a_t – пункты, куда можно поставить очередной камень. Тогда величина, характеризующая качество – Q_t(s_t, a_t), – говорит нам, насколько хорош будет ход a_t в состоянии s_t. Для YouTube одно состояние – все пользователи в сети и все имеющиеся ролики. Действие – просмотр конкретным пользователем конкретного видеоролика, а качество – насколько долго он его просматривает.

Вознаграждение R_t(s_t, a_t) – награда, которую мы получаем за выполнение действия a_t в состоянии s_t. В го награда появляется только с концом партии. Мы можем дать 1 за выигрывающий ход, – 1 за проигрывающий и 0 за любой другой. Какое-нибудь состояние может иметь высокое качество, но нулевое вознаграждение: например, если некоторое расположение камней близко к победному.

Когда DeepMind использовала уравнение вознаграждения для игр Atari, она добавляла еще один компонент: будущее. Когда мы производим какое-нибудь действие a_t (ставим камень в го), то переходим в новое состояние s_t+1 (на доске занят тот пункт, куда мы сделали ход). Уравнение вознаграждения DeepMind добавляет вознаграждение размером Q_t(s_t+1, a) за наилучшее действие в этом новом состоянии. Это позволяет искусственному интеллекту планировать свои будущие шаги в игре.

Уравнение 8 дает нам гарантию. Оно говорит, что если мы будем следовать такой схеме и обновлять качество нашей игры, то постепенно ее освоим. Более того, с помощью этого уравнения мы в итоге придем к оптимальной стратегии для любой игры – от крестиков-ноликов до шахмат и го.

Но есть одна проблема. Это уравнение не говорит нам, сколько времени придется играть, чтобы узнать качество всех различных состояний. В игре го 3^19×19 состояний, что дает примерно 1,7 × 10¹⁷² различных возможных позиций на доске. Даже очень быстрому компьютеру потребуется огромное время, чтобы сыграть их все, а ведь чтобы наша функция качества сходилась, нам нужно пройти через каждое состояние много раз. Нахождение наилучшей стратегии возможно теоретически, но не практически.

Ключевой идеей для специалистов Google DeepMind стало понимание, что качество Q_t(s_t, a_t) можно изобразить в виде нейронной сети. Вместо того чтобы узнавать, как искусственный интеллект должен играть во всех 1,7 × 10¹⁷² возможных позициях в го, разбирающийся в этой игре ИИ был представлен в таком виде: на входе позиции на доске 19 × 19, далее несколько уровней из скрытых нейронов и выходные нейроны, которые определяли следующий ход. Как только задача была переформулирована в форме нейронной сети, исследователи смогли для получения ответа использовать метод градиентного спуска (уравнение 9).

Возможно, наиболее мощная демонстрация силы такого подхода была такой: ученые взяли нейронную сеть AlphaZero, которая не умела играть в шахматы, и всего за четыре часа она освоила их на уровне лучших компьютерных программ мира, которые сами уже далеко превосходили возможности лучших шахматистов-людей. После этого AlphaZero продолжала учиться, бросая вызов себе, чтобы найти методы игры, которые непредставимы ни для человека, ни для любого компьютера.

При работе с нейронными сетями применяются все уравнения, с которыми мы встречались ранее. Мы уже использовали уравнения 1, 4, 8 и 9. Уравнение 5 применяют при изучении связей между сетями. Способ соединения нейронов – ключ к определению типа задач, которые может решить сеть. Название «Воронка» дано по структуре нейронной сети, используемой YouTube, когда есть много входных нейронов и небольшое количество выходных. Ученые обнаружили, что в других случаях более эффективными будут другие структуры. Например, для распознавания лиц и игр оптимальна ветвящаяся структура, известная под названием «сверточная нейронная сеть». Для обработки языковых текстов лучшим вариантом будет так называемая рекурсивная нейронная сеть.

Уравнения 3 и 6 применяют, когда смотрят на время, необходимое для обучения сети, – чтобы убедиться, что она обучилась надлежащим образом. Уравнение 7 лежит в основе метода, который называется «обучением без учителя»: его можно использовать, когда у нас для анализа есть миллионы разных видео, изображений или текстов и мы желаем установить самые важные закономерности, на которые стоит обратить внимание. Уравнение 2 – база байесовских нейронных сетей, важных при изучении игр, связанных с неопределенностью, – например, покера.

Итак, всего в девяти уравнениях мы находим основу для современного искусственного интеллекта. Изучите их, и вы сможете помочь создать искусственный интеллект для будущего.

Большинство из нас не знают, что все лучшие работы в области ИИ доступны всем, кто хотел бы узнать больше и уже понимает эти девять уравнений на том же уровне, что и вы сейчас. Статьи публикуются в журналах с открытым доступом, а библиотеки компьютерного кода доступны всем, кто желает создавать собственные модели. Открытость растет – от доктрины де Муавра и записных книжек Гаусса через взрывное развитие науки в конце прошлого века и до современных архивов веб-сервиса Github, где технологические гиганты складывают IT-проекты и делятся программными кодами.

Людям нужно не верить страшилкам или раздуваемой шумихе, что искусственный интеллект становится человеком, а посмотреть на историю Google. Эта компания, основанная двумя аспирантами из Калифорнии, проводит и финансирует высококачественные исследования; и почти все, что она делает, доступно широкой публике. Конечно, есть опасность, что лучшие умы уходят из университетов и идут трудиться для Google, Facebook и других компаний. Но многие из нас по-прежнему сидят в башнях из слоновой кости; и сегодня мы узнаём от Google почти столько же, сколько он извлек из нашей предыдущей работы.

Секреты «Десятки» не в самих уравнениях, а в умении их использовать и комбинировать. Если их применять бездумно, они ничего не решат.

Риск для человечества исходит не от враждебного ИИ, который захватит наш мир, – дворецкого Джарвиса из вселенной Marvel или «Саманты», соблазняющей каждого мужчину на планете в фильме «Она». Искусственный интеллект для этого недостаточно умен. Он застревает в своих ограниченных решениях. Риск скорее заключается в растущем разрыве между теми, кто обладает властью над данными, и теми, кто ею не обладает. Небольшая группа людей, знающих уравнения, имеет уровень умственного развития, какого на планете еще не было.

У тех, кто разбирается в математике, есть преимущество. Два аспиранта создали поисковую систему на основании уравнения влияния (уравнение 5). Три разработчика Google создали нейронную сеть, которая заставляет миллионы людей смотреть отупляющие видеоролики и рекламу. Раз за разом повторяется одна и та же схема: небольшое количество программистов, финансистов и игроков используют математику, чтобы доминировать над другими; иными словами, небольшая элитная группа математиков контролирует жизни тех, кто не может или не желает изучать этот код.

Не неся ответственности за свои действия, «Десятка» преобразует все аспекты мира. Равнодушная к ограничениям, она ищет оптимальные ответы на все задачи. «Десятка» может не осознавать себя, но свидетельства ее существования неоспоримы.

Теперь, когда мы знаем, как работают девять из десяти уравнений, а также силу и ограничения каждого из них, возможно, сумеем ответить на самый важный вопрос. Это тайное математическое общество, управляющее миром, – добро или зло?

Лично я сделался богаче, умнее и успешнее, следуя «Десятке», но стал ли я лучше как человек?