Глава 8. Уравнение вознаграждения

В течение пятнадцати лет в начале своей карьеры я исследовал, как животные ищут и собирают вознаграждение. Я не принимал какого-то решения, что должен этим заниматься, – просто так уж меня угораздило.

Два друга-биолога – Эймон и Стивен – как-то спросили меня, не хотел бы я съездить на день на Портленд-Билл (узкий полуостров на южном побережье Англии). Им нужны были муравьи. Эймон показывал мне, как аккуратно раскрыть небольшую трещину в скале, где насекомые могут прятаться. Казалось, всякий раз он оказывался прав, находя муравьев под выбранными камнями. Он быстро всасывал их импровизированным пылесосом в пробирку, которую нужно было взять в лабораторию.

В конце концов этого добился и я – встав чуть дальше от моих коллег под вздымающимся маяком. Это было приятное удовлетворение – втягивать колонию муравьев через оранжевую пластиковую трубку. Мы потратили пять лет на изучение того, как эти насекомые выбирают новое место для своего дома. Я создавал модели; они собирали данные.

Аналогичную цель имели прогулки по йоркширским болотам с Мадлен, которая тогда была в постдокторантуре и занималась биологией в Шеффилде: сюда летали медоносные пчелы от своего улья, чтобы собрать пыльцу с вереска. Здесь наши головы очистились от густого офисного воздуха, и я пытался связать мои уравнения с ее описаниями того, как пчелы и муравьи сообщают друг другу о пище. Мы работали вместе более десяти лет, наблюдая за тем, как разные виды общественных насекомых определяют, какие источники пищи использовать.

Многие обсуждения проходили в менее пленительных местах. Дора – тогда аспирантка в Оксфорде и первый мой друг после переезда сюда – рассказывала мне о своих голубях, когда мы сидели на холодной ступеньке у фургона с кебабами. Через несколько дней мы в кафе Jericho изучали результаты отслеживания ее птиц с помощью системы GPS. Через год вносили финальные штрихи в работу о том, как пары птиц меняют маршруты на пути домой.

Эшли тщательно конструировал Y-образные лабиринты для колюшек (мелких рыб). Я встретил его в пабе с Иэном, и мы обсудили, как можем моделировать их решения в группах. Вместе мы смотрели, как они избегают хищников и следуют друг за другом к еде.

Далее мой путь лежал за пределы Англии. Большеголовые муравьи в Австралии с Одри. Аргентинские муравьи с Крисом и Таней. Муравьи-листорезы на Кубе с Эрнесто. Домовые воробьи на юге Франции с Мишелем. Саранча из Сахары с Джеромом и Иэном. Слизевики в Японии с Тоси (а также с Одри и Таней). Цикады в Сиднее с Тедди.

Все мои коллеги тех лет теперь профессора в университетах по всему миру. Но это никогда не было нашей единственной целью. Мы люди, которые беседуют друг с другом, учатся друг у друга и решают проблемы совместно. Мы получали удовлетворение, отвечая на вопросы, и постепенно всё лучше понимали мир природы. Через пятнадцать лет я знал почти все о том, как животные принимают решения в группах. Тогда в моей голове еще не было ясности, однако, оглядываясь сейчас назад, понимаю, что практически за всем, что я тогда делал, стоит одно уравнение.

Чтобы выживать, животным нужны еда и убежище. И партнер для воспроизводства.

В основе этих трех требований для жизни лежит нечто еще более фундаментальное, что должны получать животные: информация. Они собирают информацию о еде, убежище и половой жизни исходя из собственного опыта и опыта других особей. Затем применяют ее для выживания и воспроизводства.

Муравьи – один из моих любимых примеров. Многие из них используют химический маркер-феромон, чтобы показать другим насекомым, где они были. Когда они находят лежащую на земле сладкую пищу, то оставляют метку. Другие муравьи ищут ее и следуют за ней до еды. В итоге срабатывает механизм обратной связи: все больше муравьев оставляют свои феромоны, и находить пищу можно все быстрее.

Людям тоже нужны пища, кров и партнер для воспроизводства. В прошлом мы тратили уйму времени на поиск информации, которая позволила бы нам получить и сохранить три этих важнейших элемента. В современном обществе такой поиск изменил форму. Для значительной части населения мира поиск предметов первой необходимости уже завершен, однако поиск информации о еде, жилье и сексе продолжается и расширяется: теперь он принимает форму просмотра кулинарных передач и реалити-шоу Love Island («Остров любви»); чтения сплетен о знаменитостях; изучения выставленного на продажу жилья и цен на недвижимость. Мы публикуем фотографии наших партнеров, обеда, детей и домов. Показываем всем, куда едем и что делаем. Как муравьи, мы стремимся поделиться тем, что нашли, и следовать полученным советам.

Мне неудобно признать масштаб своих ежедневных поисков информации. Я захожу в Twitter проверять уведомления; открываю почту в поисках новых писем; читаю политические новости, а затем пробегаю по спортивным. Я иду на онлайн-платформу Medium, где публикую свои тексты – чтобы увидеть, нравятся ли мои истории и нет ли там интересных комментариев.

Математический способ интерпретации моего поведения возвращает нас к игровым автоматам, упомянутым в . Каждое приложение в телефоне – все равно что дергание ручки автомата в надежде получить вознаграждение. Я тяну ручку Twitter: семь ретвитов! Теперь электронной почты: письмо с приглашением выступить. Класс, я популярен! Я тяну ручку новостей и спорта: очередная заморочка брексита или слух о трансфере. Заглядываю на платформу Medium – но никто не поставил лайк моим постам. О боже, эта ручка плохо работает.

Сейчас я представлю такую жизнь с приложениями – игровыми автоматами в виде уравнения. Вообразите, что я открываю Twitter раз в час. Вероятно, это заниженная величина, но начнем с простого предположения.

Обозначим как R_t вознаграждение, которое я получу за час t. Для простоты скажем, что R_t = 1, если кто-то сделал ретвит моего поста, и R_t = 0, если не было ни одного ретвита.

Представим вознаграждения за рабочий день с 9 до 17 часов в виде последовательности единиц и нулей. Например, она может выглядеть так:

Эти вознаграждения моделируют ретвиты внешнего мира.

Теперь нужно учесть мое внутреннее состояние. Обращаясь к этому приложению, я улучшаю свою оценку качества Twitter, его способности дать мне мгновенное ощущение самоутверждения, которое предоставляет только ретвит или лайк. Здесь мы можем использовать уравнение вознаграждения:

Кроме времени t и вознаграждения R_t сюда входят еще два символа: Q_t отражает мою оценку качества вознаграждения, а α определяет, насколько быстро я теряю уверенность при его отсутствии. Эти буквы требуют дополнительного пояснения.

Если я пишу: Q_t+1 = Q_t+1, это означает, что я увеличил Q_t на единицу. Эта идея используется в программировании внутри «цикла со счетчиком»: мы увеличиваем Q_t на 1 каждый раз, когда проходим цикл. Та же идея применяется и в уравнении вознаграждения. Но вместо прибавления 1 мы изменяем Q_t, добавляя два разных слагаемых. Первый компонент – (1 – α)Q_t – понижает оценку качества вознаграждения. Например, если мы выберем α = 0,1, на каждом шаге наша оценка будет снижаться на 1–0,1 = 90 % по сравнению с предыдущим уровнем. Это то же уравнение, которое мы сейчас используем, например, для описания того, как автомобиль каждый год падает в цене; далее мы увидим, как оно описывает испарение феромонов и других химических веществ. Второй компонент – αR_t – повышает нашу оценку стоимости вознаграждения. Если вознаграждение равно 1, добавляем α к нашей оценке.

Сложив оба компонента, можем увидеть, как работает уравнение в целом. Представьте, что я начинаю работу утром в 9 часов с оценкой Q₉ = 1. Иными словами, я на 100 % уверен, что Twitter даст мне вознаграждающий ретвит. Открываю его, но с разочарованием обнаруживаю, что R₉ = 0. Нет ретвитов. Нет вознаграждения. И я использую уравнение 8, чтобы изменить мою оценку качества на Q₁₀ = 0,9 ∙ 1 + 0,1 ∙ 0 = 0,9. Теперь я немного меньше уверен, когда открываю Twitter в 10 часов утра, однако на этот раз получаю то, что искал: R₁₀ = 1. Ретвит! Моя оценка качества не возвращается к исходному состоянию, но чуть двигается вверх: Q₁₁ = 0,9 ∙ 0,1 + 0,1 ∙ 1 = 0,91.

В 1951 году математики Герберт Роббинс и Саттон Монро доказали, что уравнение 8 всегда дает верную оценку среднего значения вознаграждения. Чтобы понять этот результат, предположим, что вероятность получения вознаграждения (ретвита) за любой конкретный час равна R–, и пусть R– = 0,6, или 60 %. Перед тем как начать ежечасную проверку Twitter, я понятия не имел о значении R–. Моя цель – оценить значение этой величины по последовательности вознаграждений, которые я получаю после открытия Twitter. Они у нас представлены в виде последовательности из 0 и 1 – 011001011… Если та продолжается бесконечно, средняя частота единиц будет R– = 60 %.

Уравнение 8 быстро начинает отражать вознаграждения: R₁₁ = 0, и поэтому Q₁₂ = 0,919; R₁₂ = 0, и поэтому Q₁₃ = 0,827 и т. д., так что к концу дня мы получаем Q₁₇ = 0,724. Каждое наблюдение приближает меня к истинному значению R–. По этой причине Q_t часто называют отслеживающей переменной: она отслеживает значение R–. Рисунок 8 иллюстрирует этот процесс.

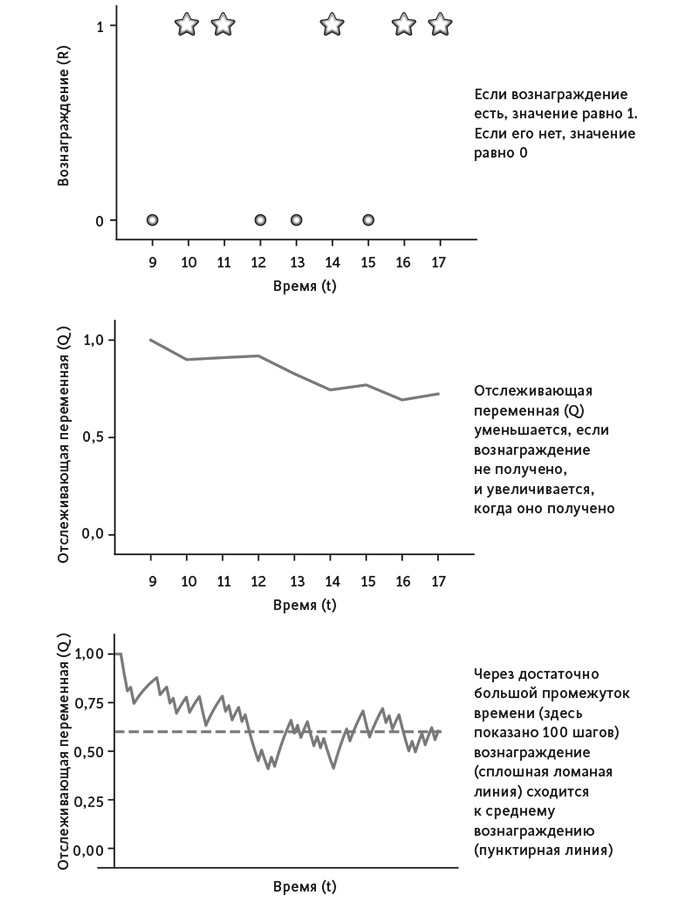
Рис. 8. Как отслеживающая переменная отслеживает вознаграждение

Роббинс и Монро показали, что для надежной оценки R– не нужно хранить всю последовательность нулей и единиц. Чтобы получать очередную оценку Q_t+1, надо знать текущую оценку Q_t и следующее вознаграждение в последовательности R_t. Если я все вычислил правильно вплоть до этого момента, то могу забыть о прошлом и сохранять только отслеживающую переменную.

Есть оговорки. Роббинс и Монро показали, что нам нужно очень медленно уменьшать со временем значение α. Помните, что α (греческая буква) – параметр, которые управляет скоростью забывания. Изначально у нас доверия нет, поэтому нужно уделять много внимания последним величинам, и поэтому α получает значение, близкое к 1. Со временем нам нужно понижать α, так что эта величина стремится к 0. Именно медленное уменьшение гарантирует, что наша оценка сходится к вознаграждению.

Представьте, что вы лежите на диване и вознаграждаете себя просмотром телевизора. На экране какой-то сериал Netflix. Первая серия – отличная (как всегда), вторая – средняя, третья – чуть лучше. Вопрос таков: сколько времени вам следует смотреть, прежде чем бросить сериал? Вашему мозгу это не особо важно, но вас это заботит. Вы хотите смотреть в выходной что-то хорошее.

Решение – использовать уравнение вознаграждения. Для телесериала хорошим значением для нашего показателя снижения доверия будет α = 0,5, или половина. Это очень высокая скорость забывания прошлого, но хорошее шоу должно постоянно дарить новые идеи.

Вот ваши действия. Вы ставите первому эпизоду оценку по 10-балльной шкале – скажем, 9. Итак, Q₁ = 9. Если смотрите серии подряд, то держите в голове число 9 и начните следующую серию. Поставьте ей оценку. Предположим, это 6. Теперь имеем Q₂ = 9/2 + 6/2 = 7,5. Удобно каждый раз округлять, так что новая оценка будет 8. Смотрим следующий эпизод. Пусть на этот раз мы ставим 7. Берем Q₂ = 8/2 + 7/2 = 7,5, снова округляем до 8.

Продолжаем в том же духе и дальше. Сила этого метода в том, что не нужно помнить, насколько сильно вам понравились предыдущие эпизоды. Вы отмечаете Q_t для последней серии в голове. Сохранять отслеживающую переменную Q_t можно не только при просмотре телесериала, но и при оценке того, нравится ли вам ходить на разные мероприятия, читать различных авторов или заниматься в классе йоги. Это единственное число для каждого занятия позволяет понимать общее вознаграждение за различную деятельность, не возвращаясь к конкретным моментам, когда вас втянули в разговор с одним скучным математиком во время выпивки после работы или когда вы повредили седалищный нерв во время йоги.

Когда бросать просмотр? Чтобы ответить на этот вопрос, нужно установить личный порог. Я использую число 7. Если качество серий падает до 7, я останавливаюсь. Это довольно жесткое правило, поскольку оно означает, что если текущий уровень 8, а очередной эпизод получает оценку 6, то у меня получается 8/2 + 6/2 = 7 и я вынужден бросить просмотр. Но мне кажется, что это справедливо. Хороший сериал должен регулярно выдавать эпизоды уровня 8, 9 и 10. Если он достигает таких высот, то переживет оценку 6 и даже 5. Например, если текущее значение Q_t = 10 и я вижу серию, которая тянет только на 5, то Q_t+1 = 10/2 + 5/2 = 7,5, округляю до 8 и могу смотреть дальше. Однако для продолжения просмотра следующий эпизод должен оказаться хорошим. На основании этого правила я посмотрел три с половиной сезона «Форс-мажоров», два сезона «Большой маленькой лжи», полтора сезона «Рассказа служанки» и два эпизода сериала «Ты».

В большинстве компьютерных игр для отслеживания ваших успехов используется только одно число – набранные очки или уровень. Очки подобны Q_t в уравнении вознаграждения: они отслеживают ваши вознаграждения. Вы выбираете, что делать дальше: каким маршрутом поедете в гоночной игре Mario Kart, какого противника хотите выследить и убить в Fortnite, какой ряд переместите в игре «2048», на какую арену отправитесь за покемоном в игре Pokémon Go – и ваш счет меняется в зависимости от ваших успехов.

Ваш мозг действует аналогично. Химическое вещество дофамин часто называют элементом системы вознаграждения мозга, и иногда люди говорят, что были «вознаграждены» приливом дофамина. Однако такая картина недостаточно детализирована. Более двадцати лет назад немецкий нейробиолог Вольфрам Шульц рассмотрел экспериментальные данные по дофамину и пришел к выводу, что «дофаминовые нейроны активируются событиями, которые лучше прогноза, не затрагиваются теми, которые настолько же хороши, как он, и подавляются теми, которые хуже его». Итак, дофамин не вознаграждение R_t, а отслеживающий сигнал Q_t. Мозг использует его для оценки вознаграждения: он дает нам наш игровой счет.

Игры удовлетворяют многие наши базовые психологические потребности – например, демонстрацию умений решать задачи или работать совместно в группах. Одна из причин того, что мы играем в игры, возможно, в том, что те измеряют степень выполнения задач. В реальной жизни все запутано. Когда мы принимаем какие-то решения на работе и дома, результаты порой непросты, и о вознаграждении судить сложно. В играх же все легко: если мы действуем правильно, то получаем вознаграждение; если плохо, то терпим убытки. Игры устраняют неопределенность и позволяют нашей дофаминовой системе заниматься тем, что ей больше всего нравится: отслеживать вознаграждения. Простота ведения счета в какой-нибудь игре, которая обеспечивается одной-единственной отслеживающей переменной, отражает работу наших биологических систем вознаграждения.

Индустрия компьютерных игр разобралась с уравнением вознаграждения. Одно исследование, в котором изучались британцы, ежедневно после работы игравшие в Block! (головоломка типа «Тетриса») или пользовавшиеся приложением для медитации Headspace, установило, что игроки в Block! лучше восстанавливались после рабочих стрессов. Эмили Коллинз, постдокторант из Университета Бата, проводившая эксперимент, позже заметила: «Медитация порой хороша для расслабления, но видеоигры обеспечивают психологическую отстраненность. Вы получаете внутренние вознаграждения и реальное ощущения контроля».

Один разработчик компьютерных игр – Niantic – использовал наше желание получать вознаграждение для разработки игр, которые заставляют нас двигаться. В самой знаменитой их игре – Pokémon Go – нужно выходить в реальный мир и «собирать» маленьких созданий, покемонов, с помощью мобильного телефона. Эта игра поощряет к прогулкам, поиску монстриков, высиживанию их яиц и работе в команде. Если вы видели группу людей, стоящих перед местной церковью или библиотекой и бездумно стучавших по своим телефонам, то наверняка это были охотники за покемонами, собравшимися для захвата арены.

А сейчас я вам расскажу кое-что личное. О моей жене. Ловиса Самптер – очень успешная женщина. Она доцент в департаменте математического образования Стокгольмского университета. Учит студентов, которые сами однажды станут преподавателями в школах; организует крупные международные конференции и выступает на них; курирует магистров и аспирантов; пишет документы, определяющие политику образования, и ведет вдохновляющие беседы с учителями. Ловиса также квалифицированный преподаватель йоги. Я мог бы написать целую книгу о том, какая замечательная у меня жена, и большая часть была бы посвящена тому, как она терпела меня все это время и организовала нашу семейную жизнь.

Но личное – другое. Все, кто встречался с Ловисой, знают, какая она замечательная. Ее таланты – не секрет, а установленный эмпирически факт. Однако Ловиса добилась всего этого, живя с 2004 года с постоянными болями. В 2018 году ей поставили диагноз «фибромиалгия» – состояние, которое характеризуется хронической болью во всем теле; в первую очередь это проблема нервной системы. Организм Ловисы постоянно посылает в мозг болевые сигналы. Затем система отслеживания болей отправляет предупреждения вместо вознаграждения. Любая незначительная боль усиливается, из-за чего трудно спать, концентрироваться и оставаться терпимыми к близким. Лекарства неизвестны. Именно поэтому игра Pokémon Go стала важной частью жизни Ловисы: там она может получить какие-то вознаграждения, в которых ей отказывает ее организм.

Игра позволяет Ловисе сосредоточиться во время болей на чем-то другом, а также гарантирует долгие прогулки каждый день. Благодаря ей Ловиса нашла новых друзей, вместе с которыми «сражается на аренах» и участвует в «рейдах». Многие из таких игроков имеют работу, связанную со стрессами, – например, медсестры или врачи. Среди них есть также учителя и IT-специалисты, студенты и другая молодежь. Благодаря группе Ловисы появилась минимум одна семейная пара. Есть также немало людей, которых другая социальная среда, возможно, выталкивала, – например, безработная молодежь, безвылазно игравшая дома в PlayStation, которую Pokémon Go снова вывела во внешний мир.

У всех поклонников Pokémon Go имеется своя история о том, как игра им помогла. Одна пенсионерка начала играть, чтобы вместе со внуками делать то, что им может понравиться. Как и многие ее ровесники, она сравнивает это с хоровым обществом. «Идете в рейд и делаете свое дело. Преимущество в том, что вы можете хоть беседовать с другими, хоть просто спокойно стоять».

Еще у одного из товарищей Ловисы по игре есть партнер, больной раком. Игра для него – шанс выбраться наружу и подумать о чем-то другом. Некоторые страдали от долгой депрессии и получают удовольствие от помощи новичкам. У новой подруги Ловисы по игре – Сесилии – синдром Аспергера и синдром дефицита внимания и гиперактивности, один из симптомов – желание копить вещи, например рецепты и журналы. «Теперь я могу собирать и организовывать, не становясь скопидомом. И при этом получаю физическую нагрузку!» – сказала она Ловисе. Сесилия грубовато-пряма, с юмором, и это помогает Ловисе справляться со своими ощущениями.

Pokémon Go приносит стабильность в жизнь Ловисы и других людей. Вознаграждения идут устойчивым потоком – пусть и в непредсказуемое время, зато регулярно. «Это не лекарство, а скорее своего рода управление симптомами, – говорит мне Ловиса. – Это механизм выживания».

Ловиса и ее приятели всего лишь одна группа из многих разбросанных по планете любителей покемонов, жизнь которых улучшилась благодаря прогулкам и поиску вознаграждения. Йенни Солхейм Фуллер, старший менеджер, отвечающий в Niantic за гражданское и социальное влияние, рассказала мне об одном игроке, который страдал от посттравматического стрессового расстройства после возвращения из зарубежной поездки: «Стремление к успехам в игре вынуждало его выходить из дома и сосредоточиваться не на ПТСР, а на чем-то еще». Йенни добавляет: «Еще одна большая группа – аутисты. Мы встречали множество родителей, дети которых отличались невероятной чувствительностью к шуму и хаосу вокруг и не могли выходить на улицу. Сейчас же они стоят перед художественной школой, проводя рейды и разговаривая с другими людьми».

Йенни получала сообщения от онкобольных, благодаривших ее за игру, которая помогла им пережить тяжелое время. Она прочитала письмо от сына одного человека, пятнадцать лет страдавшего диабетом, а потом начавшего играть в Pokémon Go. «Сейчас он добрался до сорокового уровня, самого высокого, – писал сын. – Он стал одним из самых чутких пожилых игроков. Диабет больше не угрожает его здоровью, и ему уже не нужны инъекции».

Это всего лишь одна из историй, которые заставили Йенни и ее коллег плакать; когда она читала их мне, я тоже плакал. Ловиса достигла сорокового уровня летом 2018 года. И пусть внешнему миру это может показаться не самым впечатляющим ее достижением, я вижу, как она использовала вознаграждения, чтобы справиться с болью.

Результат Герберта Роббинса и Саттона Монро стал начальной точкой для области математики, используемой при обнаружении сигналов; она стала развиваться в 1950-х и 1960-х. Математики показали, что отслеживающую переменную Q_t можно использовать для оценки изменений в нашей среде. Вознаграждения – хорошие и плохие – можно наблюдать. В 1960 году Рудольф Эмиль Калман опубликовал основополагающую работу, показывающую, как надежно отфильтровать шум в вознаграждениях, чтобы раскрыть истинный сигнал. Его метод использовали, чтобы оценивать скорость и положение объектов в роторах, что стало существенным шагом в разработке автоматических датчиков.

Затем теория обнаружения сигналов была соединена с новой областью – математической теорией управления. Ирмгард Флюгге-Лотц уже разработала систему прерывистого автоматического управления, которая давала возможность автоматически реагировать включением и выключением на изменения в температуре воздуха или турбулентности воздуха. Ее работа, наряду с трудами других специалистов по теории управления, позволила инженерам проектировать автоматизированные системы, которые отслеживают изменения в окружающей среде и реагируют на них. Сначала их применили в термостатах, реагирующих на температуру в наших холодильниках и домах. Эти же уравнения легли в основу крейсерского режима для самолетов. Их также использовали для выравнивания зеркал в мощных телескопах, заглядывающих далеко во Вселенную. Именно эта математика управляла двигателем, который отвечал за начальные стадии торможения при приближении лунного модуля «Аполлона-11» к поверхности нашего спутника. Сегодня эти методы используются в роботах, которые трудятся на производственных линиях Tesla и BMW.

Теория управления создала мир устойчивых решений. Инженеры написали уравнения и потребовали, чтобы мир следовал этим правилам. Во многих случаях это прекрасно работало. Но мир неустойчив: бывают флуктуации и случайные события.

1960-е заканчивались новой контркультурой, бросавшей вызов установившемуся порядку, и «Десятка» тоже претерпела революцию. Акценты сместились с устойчивых линейных систем к неустойчивым, хаотичным и нелинейным. Именно такая математика повлияла на меня, когда я был молодым аспирантом в конце 1990-х, и я взялся за изучение всех этих математических теорий с экзотическими названиями: бабочка хаоса, модели песчаных лавин, критические лесные пожары, бифуркации в седловых точках, самоорганизация, степенные законы, критические точки… Каждая новая модель помогала объяснить сложность, которую мы видели вокруг.

Ключевой оказалась такая идея: устойчивость желательна не всегда. Новые математические модели описывали, как меняются экологические и социальные системы: не всегда возвращаясь обратно к тому же устойчивому состоянию, но иногда колеблясь между состояниями. Они описывали, как муравьи создают тропинки к пище, как нейроны синхронно возбуждаются, как рыба плавает в косяках и как взаимодействуют биологические виды. Они рассказывали, как люди принимали решения, – и с точки зрения процессов внутри мозга, и в плане обсуждения в группах. В результате участники «Десятки» смогли занять должности на кафедрах биологии, химии и физиологии.

Именно эти математические методы я применял к данным, собранным биологами, с которыми работал.

На своем телефоне я открываю не только Twitter, но и множество приложений. Так и у муравьев и пчел есть не один источник пищи, а сразу несколько, и животные могут выбирать. На игровых автоматах есть много рычагов, и у нас нет времени дергать все. Задача в том, чтобы определить, какой рычаг тянуть. Мы знаем, что, потянув за один из них, можем получить достаточно хорошее представление о доступных вознаграждениях от этого игрового автомата. Но если мы проведем все время, дергая за этот рычаг, то не узнаем, что могут предложить другие машины. Это явление известно под названием «дилемма разведки/эксплуатации». Сколько времени тратить на использование уже известного, а сколько на изучение менее знакомых альтернативных вариантов?

Для решения этой задачи муравьи применяют химические вещества – феромоны. Их количество отражает оценку Q_t того, что имеется какой-то источник пищи. Теперь представьте, что у насекомых есть два источника с различными феромоновыми следами к каждому. Чтобы выбрать, каким путем идти, каждый муравей сравнивает количество феромона на обоих следах. Чем его больше, тем выше вероятность, что муравей последует этим маршрутом.

Выбор каждого следующего насекомого приводит к процессу подкрепления: чем больше муравьев пойдет по определенному пути и получит вознаграждение, тем вероятнее, что их сотоварищи отправятся тем же маршрутом. Пути с активным трафиком получают подкрепление; другие забрасываются. Это наблюдение можно сформулировать в рамках уравнения 9, где дополнительный коэффициент учитывает выбор муравьев. Вот один из примеров:

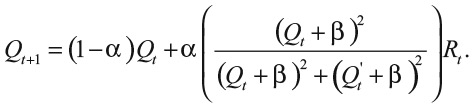
Новый коэффициент учитывает, как муравей выбирает между двумя альтернативными путями. Величину Q_t можно представлять как количество феромона на пути к одному потенциальному источнику пищи, а Q'_t – на пути к другому. Теперь у нас две отслеживающие переменные (Q _t и Q'_t) – по одной для каждого источника или (если мы моделируем использование соцсетей) по одной для каждого приложения в телефоне.

Когда сталкиваешься с новым запутанным уравнением с кучей параметров, всегда полезно рассмотреть сначала более простой вариант. Взглянем на новый коэффициент без квадратов:

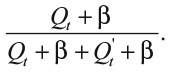
Если β = 0, это просто доля, которую одна отслеживающая переменная составляет от их суммы. Соответственно, вероятность того, что муравей использует конкретное вознаграждение, пропорциональна доле отслеживающей переменной для него. Теперь посмотрим, что произойдет при β = 100. Поскольку Q_t заключена между 0 и 1, она невелика по сравнению с числом 100, так что вышеуказанная дробь примерно равна 100 / (100 + 100) = 1/2. Вероятность того, что муравей будет использовать определенное вознаграждение, равна 0,5 (или пятьдесят на пятьдесят).

Проблема баланса между разведкой и эксплуатацией превращается в проблему нахождения оптимального уровня подкрепления маршрута. Это то же, что задача нахождения правильного значения β. Если подкрепление сильное (значение β очень мало), муравьи всегда следуют по пути с самым сильным запахом. Очень быстро второй источник забрасывается (насекомые перестают его посещать), и даже если он станет лучше, никто о нем не узнает. В результате муравьи оказываются прикованными к тому источнику, который казался лучше первоначально, даже если потом качество изменилось.

Слишком слабое подкрепление (значение β очень велико) приводит к противоположной беде. В этом случае насекомые выбирают маршруты наугад и не пользуются своими знаниями о том, какой из них лучше.

Ответ на задачу разведки и эксплуатации включает неожиданный поворот. Оказывается, решение дилеммы оптимального подкрепления связано с другим понятием, которое обычно возникает в совершенно другом контексте: критическими точками.

Поясню: критические (переломные) точки – моменты, когда накапливается какая-то критическая масса и система резко переходит из одного состояния в другое: например, мода внезапно распространяется после того, как авторитетные люди стали рекламировать этот бренд, или вспыхивает бунт, когда маленькая группа агитаторов заводит протестующих. В каждом из этих и во многих других примерах подкрепление представлений приводит к внезапным переменам состояния. То же у муравьев – формирование феромонового маршрута происходит при достижении критической точки: путь начинается, когда небольшая группа муравьев решает двигаться к пище одной дорогой.

И вот удивительный вывод: наилучший способ сбалансировать разведку и эксплуатацию – чтобы муравьи оставались в состоянии, близком к критической точке. Если насекомые отойдут от нее, то слишком многие из них будут замкнуты на один источник пищи; они не смогут переключиться, когда появится что-то лучшее. Но если этому источнику будет привержено недостаточно насекомых и ситуация не дойдет до критической точки, то муравьи не смогут сосредоточиться на оптимальной пище. Они должны найти между разведкой и эксплуатацией золотую середину.

Муравьи эволюционировали так, чтобы оставаться в критической точке. Один из моих любимых примеров того, как они добиваются этого равновесия, обнаружила биолог Одри Дюссютур, работавшая с большеголовыми муравьями (этот вид получил свое название за необычно крупную голову). У них много поводов гордиться своей головой: они колонизировали большую часть тропического и субтропического мира, выиграв конкуренцию у других местных видов. Одри выяснила, что они используют два вида феромонов: один испаряется медленно и дает слабое подкрепление, другой же испаряется быстро и дает очень сильное подкрепление.

Мы с математиком Стэмом Николисом разработали модель с двумя уравнениями вознаграждения: одно для слабого, но длительно действующего феромона, а другое – для сильного, но короткоживущего. Мы показали, что комбинация этих двух феромонов позволила муравьям оставаться в районе критической точки. В нашей модели муравьи могли отслеживать два разных источника, переключаясь между ними всякий раз, когда качество пищи менялось. Одри подтвердила наши прогнозы экспериментально: когда она меняла качество еды, большеголовые муравьи переключали свои усилия на лучший источник.

Жизнь около критической точки характерна не только для муравьев. Для многих животных это бесконечное казино с игровыми автоматами. Не сидит ли в тех кустах какой-нибудь хищник? Есть ли еда там, где я нашел ее вчера? Где можно найти убежище на ночь? Чтобы выжить в этих условиях, эволюция довела животных до критических точек. Этот феномен я обнаруживал раз за разом в течение пятнадцати лет, когда изучал их поведение: саранча перемещается с такой плотностью, которая позволяет быстро менять направление движения; косяки рыб внезапно рассыпаются при нападении акул; скворцы в стаях дружно уворачиваются от ястреба. Двигаясь вместе, жертвы путают хищника.

Животные эволюционировали до критической точки. Они находятся в состоянии постоянной коллективной сознательности – переключаются от одного решения на другое, быстро реагируют на изменения. Для них это вопрос выживания.

А как насчет людей? Застряли ли мы на какой-нибудь критической точке? И если да, должны ли мы там оставаться?

В 2016 году Тристан Харрис обрушился на социальные сети. Предыдущие три года он работал в Google, но похоже было, что он этим сыт. Харрис ушел из Google и опубликовал на платформе Medium свой манифест. Заглавие утверждало: «Технологии захватывают ваш разум», а двенадцатиминутное содержание объясняло, как они это делают.

Аналогия, которую он выбрал для соцсетей, вам уже знакома: игровой автомат. По его словам, технологические гиганты фактически положили такие автоматы в карманы нескольких миллиардов человек. Уведомления, твиты, электронные письма, ленты Instagram и пролистывания-свайпы Tinder просят нас «потянуть за рычаг» и узнать, выиграли ли мы. Они прерывали наш день постоянными напоминаниями, а затем пропитывали нас страхом пропустить что-нибудь, если мы не дернем рычаг вовремя. Они соблазняли нас одобрением от наших друзей и побуждали отвечать взаимностью, ставя лайки и делясь публикациями, когда мы дергали рычаги одновременно с другими. Все это происходило в соответствии с собственными планами технологических компаний – заставить вас просмотреть рекламу и переходить по оплаченным ссылкам. Google, Apple и Facebook создали гигантское онлайн-казино и загребали прибыли. Наши карманные игровые автоматы вызывают такое привыкание, поскольку постоянно ставят нас перед необходимостью решать задачу разведки и эксплуатации. При этом социальные сети не простой игровой автомат: здесь тысячи ручек, и за все нужно потянуть, чтобы узнать, что происходит.

Ученым давно известно, какие проблемы доставляет мозгу животных наличие нескольких ручек. В 1978 году Джон Кребс и Алекс Касельник провели в Оксфордшире эксперимент с большими синицами. Они предложили птицам две разные жердочки. Насесты были сконструированы так, что, когда синица садилась туда, иногда выпадала еда. Вероятность этого события была разной: на одной жердочке больше, чем на другой. Кребс и Касельник обнаружили, что в случаях, когда один насест был намного выгоднее другого, птицы быстро сосредоточивались только на нем. Но когда насесты были схожими, задача для птиц оказывалась сложной. Они перелетали между жердочками туда и обратно, пытаясь проверить, какая лучше. В моей терминологии синицы подошли близко к критической точке.

Математик Питер Тейлор показал, что уравнение вознаграждения полностью согласуется с этим результатом. Чем труднее выбрать вознаграждение, тем больше исследований-разведки требуется. Мы делаем то же, что и эти синицы, только у нас больше вариантов выбора. Мы открываем приложение за приложением. Но проблема не в доступности всех этих вознаграждений – она в желании мозга разведывать и эксплуатировать. Мы желаем быть уверенными в том, что знаем, где можно найти каждое из потенциальных вознаграждений. Нас подталкивают к критической точке.

Между использованием одного источника и нескольких огромная разница. Когда вы читаете какую-то книгу, играете в Mario Kart или Pokémon Go, смотрите «Игру престолов», играете в теннис с другом или идете в спортзал, вы сосредоточены только на одном источнике вознаграждения. Вам нравятся повторяющиеся сигналы о найденном предмете или звонки, отмечающие пройденный круг в гонке.

Ваше уравнение вознаграждения сходится к устойчивому состоянию. Это уравнение 1950-х, для которого Роббинс и Монро доказали устойчивую сходимость. Вы узнаёте, что сулит такая деятельность, и ваша уверенность медленно, но верно начинает соответствовать ожидаемому вознаграждению. Именно эта привычная стабильность и дарит удовольствие.

А когда вы пользуетесь соцсетями, то исследуете-разведываете и эксплуатируете много разных источников вознаграждения. На деле вы вообще не собираете вознаграждения, а отслеживаете неопределенную среду. Вспомните, что дофамин не вознаграждение, поэтому вы не получаете удовольствия. Вы в режиме выживания собираете как можно больше информации. Проблема не обязательно состоит в неограниченной доступности вознаграждений, она в том, что вам надо следить за всеми потенциальными источниками вознаграждения; это и делает вашу жизнь трудной. Вы подводите свой мозг к критической точке – ставите его на порог хаоса, перемещаете в переходную стадию. Неудивительно, что у вас стресс.

И в критической точке не только ваш мозг: там все общество в целом. Мы подобны муравьям, которые неистово носятся вокруг, пытаясь отслеживать источники информации. А те постоянно двигаются, меняют качество, иногда исчезают. Что же вы можете сделать с этой проблемой?

Центр гуманных технологий – организация, одним из сооснователей которой был Тристан Харрис, – предлагает рекомендации, как взять под контроль и увести разум от критической точки. Отключите все уведомления на телефоне, чтобы вас не прерывали постоянно. Измените настройки экрана, чтобы значки были неяркими и меньше бросались в глаза.

По большей части я согласен с советами Харриса. Это здравый смысл. Однако из того, как муравьи пользуются уравнением вознаграждения, можно извлечь не такие очевидные, но, возможно, даже более полезные идеи.

Во-первых, вы должны осознать невероятную мощь того, что ваш разум и общество в целом находятся в районе критической точки. Не случайно самыми экологически успешными видами муравьев стали те, которые используют феромоны наиболее эффективно. То же касается и перехода людей к переломным точкам. Они могут вызывать у вас стресс как у индивидуума, но общество на пороге критической точки способно быстрее генерировать и распространять новые идеи. Подумайте о множестве идей, которые появились вследствие движения или . Эти кампании действительно заставили людей узнать о проблемах и смогли привести к переменам. Или, если вы придерживаетесь других политических убеждений, посмотрите на выборы Трампа или . Подумайте о том, как появились эти идеи, и о реакции на них с обеих сторон.

Сегодня мы чаще вовлечены в политические дискуссии. Когда дело доходит до политических причин, то молодежь сейчас активнее, чем когда-либо, – как в интернете, так и в реальной жизни. Мы словно стая птиц, кружащаяся в вечернем небе. Мы будто косяк рыб, носящийся при приближении хищника. Мы как пчелиный рой, летящий к новому дому; как колония муравьев, прочесывающая лес в поисках пищи. Мы человеческая толпа, просматривающая новости.

Оказывайтесь в этой критической точке и наслаждайтесь свободой в ней. Читайте одну новостную статью за другой. Получайте информацию, принимайте новые идеи и следуйте своим интересам. При написании этой книги я провел бессчетные часы в поисковой системе Google Scholar, просматривая научные статьи, уточняя, кто кого цитировал, и решая, какие научные вопросы важны. Общайтесь с людьми в Сети. Спорьте при необходимости. Отправьте письмо какому-нибудь полоумному старому профессору, который пишет для Quillette. Станьте частью информационного потока. Затем, когда вы проведете около часа в этой критической точке, я расскажу вам о второй идее, на которую наткнулся, глядя на муравьев.

Я понимаю, что мог создать у вас впечатление, будто муравьи – гиперактивные фанаты игровых автоматов. Это правда, когда они трудятся, и некоторые муравьи действительно работают очень усердно. Однако многие из них весьма ленивы. В любой конкретный момент большинство муравьев ничего не делают. Пока меньшая часть сообщества бегают как сумасшедшие, оценивая и собирая пищу, большинство их сотоварищей просто бездействуют. Отчасти это связано с посменной работой; не все муравьи активны одновременно. Но в колониях также много насекомых, которые трудятся очень мало, редко выходят наружу и не участвуют в уборке. Почему муравьи в своей эволюции дошли до такой апатии, никто пока точно не знает, но если мы собираемся восхищаться меньшинством за его высочайшую активность, то нужно отдать должное и большинству за их расслабленное отношение к жизни.

Итак, когда вы уже некоторое время побыли в критической точке, поживите как ленивый муравей. Отрешитесь от всего. Поставьте «Игру престолов» на автоматическое воспроизведение. Посмотрите снова сериал «Друзья» от первого эпизода до последнего. Проведите неделю или месяц, собирая всех покемонов. Конечно, следует добавить все высоконравственные занятия вроде рыбалки, прогулок или сидения на крыльце. Но главное при этом – расслабляться без телефона. Не обращайте внимания на новости и бесконечные электронные письма, где вас указывают в качестве адресата копии. Не волнуйтесь, о них побеспокоится кто-то другой. Это вовсе не обязательно должно быть вашей заботой.

Уравнение вознаграждения говорит вам, что нужно сосредоточиться на настоящем, а не зацикливаться на прошлом. Помните то единственное число, что держите в голове. Если что-то происходит, обновите его; если нет, пусть ваша оценка чуть-чуть уменьшится. Убедитесь, что вы ощущаете разницу между устойчивыми вознаграждениями, которые продолжают поступать (пусть и нерегулярно) независимо от ваших действий, и неустойчивыми, которые со временем меняют свою природу. Устойчивые вознаграждения можно найти в дружбе и в личных отношениях; в книгах, фильмах, телевизоре; в долгих прогулках и рыбной ловле; в играх «2048» и Pokémon Go. Неустойчивые есть в социальных сетях, поиске партнера в Tinder, на большинстве рабочих мест и часто (хотим мы это признавать или нет) – в нашей семейной жизни. Не бойтесь в таких ситуациях вести разведку и эксплуатацию, однако помните, что максимальную отдачу от вознаграждений можно найти, находясь в критической точке. Так что прежде чем неустойчивые вознаграждения опрокинут вас в нежелательное место, найдите дорогу обратно к устойчивости.