Книга: Десять уравнений, которые правят миром. И как их можете использовать вы
Назад: Глава 9. Уравнение обучения
Дальше: Благодарности
Глава 10. Универсальное уравнение
Если… то…
Я набрал в телефоне запрос: «Кто в этом сезоне лучше – Месси или Криштиану Роналду?»
Я посмотрел на Людвига, Олофа и Антона, которые стояли перед экраном ноутбука. Людвиг нервно переступил с ноги на ногу: сначала тестируется его часть кода. Сможет ли футбольный бот преобразовать мою английскую фразу в язык, который ему понятен?
На экране побежал текст – результат работы мозга этого бота. Мой вопрос стал таким:
{цель: сравнить; контакт: {Криштиану Роналду, Месси}; настроение: нейтральное; промежуток времени: сезон}.
Бот справился! Он понял, что я имею в виду. Теперь очередь Олофа нервничать. Он должен был смоделировать игровые качества. Я не определил интересующий меня промежуток времени, но бот по умолчанию взял недавние матчи. Алгоритм Олофа может классифицировать характеристики как «плохие», «средние», «хорошие» и «отличные». Сейчас бота попросили оценить и сравнить двух отличных игроков.
Бот решил взять {мера: удары; турнир: Лига чемпионов}, чтобы сообщить о произведенных ударах и забитых голах в единственном турнире, где они играли оба. Мы могли видеть ответы на экранах: бот определил, кого из игроков он считает лучшим. Теперь осталось отправить эту информацию обратно на мой телефон – не в виде фигурных скобок, двоеточий и краткого текста, а в виде фраз, которые я мог бы читать.
Антон, который должен был конструировать ответы, сказал: «Существует больше 100 тысяч фраз, которые он может сказать. Различные способы составления предложений и выбора слов. Мне интересно, что он выберет».
Я смотрел на свой телефон. Потребовалось время. Нам определенно нужно поработать над пользовательским интерфейсом…
Наконец он ответил: «Из этих двух игроков я считаю лучшим Лионеля Месси. Он забил шесть раз и имеет отличные точки ударов в этом сезоне». Бот прислал мне ссылку на карту ударов со всеми ударами и голами футболиста в Лиге чемпионов. Конечно, по упоминанию «точек ударов» видно, что писал бот, но в такой формулировке было что-то очаровательное. И по сути моего вопроса он дал правильный ответ.
* * *
Студенты сконструировали этого футбольного бота частично с помощью математики, с которой мы познакомились в этой книге. Людвиг использовал уравнение обучения, чтобы научить программу понимать вопросы о футболе. Олоф применил уравнение умений, чтобы оценивать игроков, а уравнение суждений – чтобы их сравнивать. Затем Антон связал всё воедино с помощью одного финального уравнения – «Если… то…».
Прежде чем мы сосредоточимся на нем, я хочу посмотреть, на какой стадии нашего путешествия в математику мы находимся. Немного подумаем о том, что мы узнали.
Понимание уравнений может происходить на разных уровнях. Вы способны погружаться в их математические глубины, чтобы разобраться, как именно они работают и как их использовать. Если ваша цель – стать специалистом по обработке данных или статистиком в Snapchat, баскетбольном клубе или инвестиционном банке, вам необходимо совершить такое погружение. Эта книга – только начало.
Вы можете использовать десять уравнений иначе – менее техническим способом, мягче. Вы можете применить их для управления процессом принятия решений и для собственного представления о мире. Я полагаю, что вы можете использовать десять уравнений, чтобы стать лучше.
В западном мышлении исходные «если… то…» содержались в десяти заповедях. Если сегодня день субботний, то свято чти его. Если у тебя будут другие боги, то ты не предстанешь предо мной. Если у твоего соседа привлекательная жена, то ты не должен желать ее. И так далее. Проблема заповедей в том, что они негибкие и через несколько тысячелетий кажутся несколько устаревшими.
Девять уравнений, изученных нами, совсем другие. Они не устанавливают правил, что вам нужно делать в тех или иных ситуациях. Они предлагают определенный подход к жизни. Помните, как Эми в туалете услышала злые слова Рэйчел? Или как парадокс дружбы помог нам увидеть, что мы напрасно жаждем социального успеха других людей? Или когда вы раскладываете друзей по типам с помощью уравнения рекламы? В каждой из этих ситуаций я не говорил действующим лицам, что им следует делать на основании какого-то заранее определенного морального компаса. Я рассмотрел данные, определил корректную модель и пришел к разумному выводу.
Десять уравнений дают больше гибкости, чем десять заповедей. Они могут справляться с гораздо более широким кругом проблем и дать более детальные советы. Ставлю ли я десять уравнений выше десяти заповедей? Да, конечно. У нас были тысячелетия, чтобы развивать мышление: со времен исходной «Десятки» мы нашли способы лучше думать о проблемах. Я ставлю десять уравнений выше не только христианства, но и многих других подходов к жизни. То, как данные и модели сочетаются между собой, противостоя бессмыслице, придает математике чистую честность, которая позволяет ей подняться над любыми другими способами мышления.
Математическое знание – как дополнительный уровень интеллекта. Я также считаю (хотя это более спорно), что изучить десять уравнений – наша моральная обязанность. Я даже полагаю, что в целом уже проделанная работа участников «Десятки» благо для человечества. Не всегда, но чаще да. Изучая эти уравнения, вы помогаете не только себе, но и другим.
Такой вывод может показаться неожиданным, если учесть, что участники «Десятки» часто имеют преимущество перед теми, кто не обладает такими навыками. Может также показаться, что этот вывод противоречит философской позиции проверяемости, описанной Алфредом Айером, который говорил, что нельзя ожидать, чтобы в математике нашлись разумные ответы на моральные вопросы. Но вот во что я верю и что буду сейчас отстаивать. «Десятка» – это сила добра.
* * *
Чтобы выяснить, где в математике можно найти мораль, сначала нужно понять, где ее найти нельзя. С помощью метода исключения мы должны определить, что именно в математическом мышлении может подсказать нам, какие поступки «правильные».
Наше последнее уравнение «Если… то…» не одно уравнение, а сокращенное наименование множества алгоритмов, которые можно записывать в виде последовательности операторов «если… то…» и циклов «повторять… пока». Такие операторы – основа программирования. Например, в футбольном боте, созданном Антоном, мы найдем команды вроде:
если ключевые передачи > 5, то печатать («Он сделал много важных передач»)
Такого рода команды в сочетании со входными данными определяют, что будет на выходе.
В 1950-х, 1960-х и 1970-х зарождавшаяся информатика обнаружила целый ряд алгоритмов для обработки и организации данных. Одним из самых первых примеров был алгоритм сортировки слиянием, впервые предложенный Джоном фон Нейманом в 1945 году для сортировки чисел или по алфавиту. Чтобы понять, как он работает, сначала подумайте, как объединить два уже отсортированных списка. Например, у меня есть список букв в алфавитном порядке {A,G,M,X} и другой {C,E,H,V}. Чтобы создать сортированный список, объединяющий оба компонента, мне нужно идти слева направо по обоим спискам и ставить букву, которая идет раньше по алфавиту, в новый, а затем выбрасывать ее из исходного.
Попробуем. Сначала я сравниваю два первых элемента списков – А и С. Поскольку А в алфавите идет раньше, я помещаю ее в новый список и убираю из текущего. Теперь у меня три списка: новый {A}, первоначальные {G,M,X} и {C,E,H,V}. Я снова сравниваю первые элементы исходных списков, G и C, и добавляю C в новый список. Он принимает вид {A,C}. Теперь я сравниваю G и E, отправляя в новый список E: {A,C,E}. Это повторяется, пока я не получу сортированный список {A,C,E,G,H,M,V,X} и два пустых исходных.
Чтобы перейти от слияния уже отсортированных списков к сортировке произвольных, фон Нейман предложил стратегию, основанную на принципе «разделяй и властвуй». Полный список делится на более мелкие, и задача для каждого из них сводится к тому же методу – слиянию уже сортированных списков.
Предположим, мой первоначальный список таков: {X,G,A,M}. Сначала мы сливаем буквы {X} и {G}, получая {G,X}, и буквы {A} и {M}, получая {A,M}. Элегантность такого подхода в том, что на всех уровнях используется одна и та же техника. Разделив исходный список на достаточно мелкие части, мы в итоге приходим к списку, который гарантированно будет отсортирован, то есть к отдельным буквам. Затем, используя наше умение сливать два сортированных списка, мы гарантируем, что все создаваемые нами списки также будут отсортированы (см. рис. 10). Сортировка слиянием никогда не ошибается.
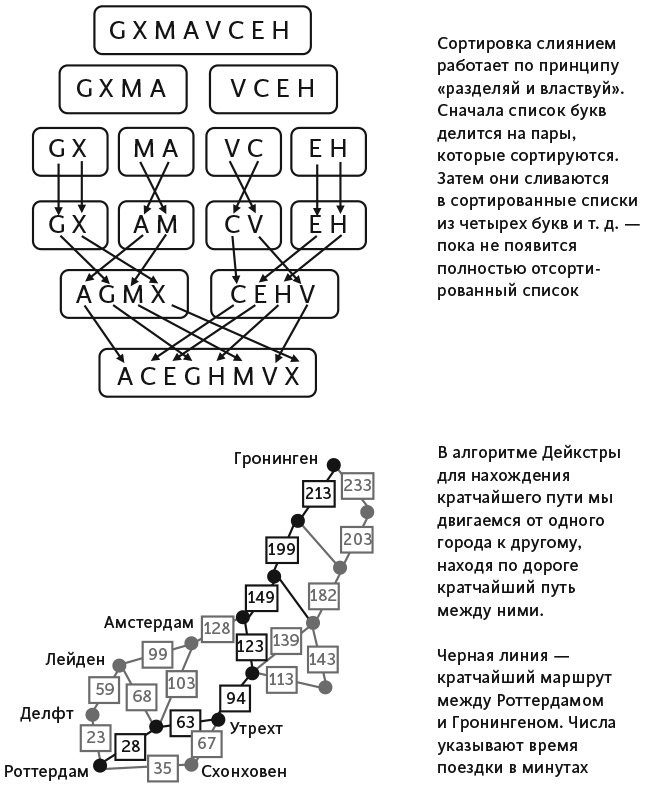
Рис. 10. Иллюстрация сортировки слиянием и алгоритма Дейкстры
Еще один пример – алгоритм Дейкстры, определяющий кратчайший путь между двумя точками. Голландский физик и программист Эдсгер Дейкстра разработал свой алгоритм в 1953 году, чтобы продемонстрировать «некомпьютерным людям» (как он их называл), что компьютеры могут быть полезными при расчете самого быстрого маршрута между двумя нидерландскими городами. На придумывание алгоритма у него ушло всего двадцать минут – он сидел в одном из амстердамских кафе. Позже он рассказывал журналу Communications of the ACM: «Одна из причин его красоты – отсутствие у меня карандаша и бумаги. Без них вы практически вынуждены избегать всех сложностей, которых можно избежать».
Представьте, что вы хотите проехать из Роттердама в Гронинген. Алгоритм Дейкстры предписывает вам сначала определить время поездки от Роттердама до всех соседних с ним городов. Процесс показан на рисунке 10. Например, Делфт получит 23 минуты, Гауда – 28, а Схонховен – 35. Следующий шаг – рассмотреть все соседние для этих трех городов и найти кратчайшее время пути до них. Например, от Гауды до Утрехта 35 минут, а от Схонховена до Утрехта – 32 минуты; поэтому кратчайшее общее время пути до Утрехта составляет 28 + 35 = 63 минуты через Гауду (это меньше, чем 35 + 32 = 67 минут через Схонховен). Алгоритм постепенно продвигается по территории Нидерландов, фиксируя кратчайшее расстояние до каждого города. Поскольку он каждый раз вычисляет кратчайший путь до любого города, то при добавлении нового города гарантировано, что до него тоже будет найден кратчайший путь. Алгоритм рассчитан не на конкретный Гронинген, он маркирует расстояния до всех городов; но когда в расчетах дело дойдет до него, алгоритм гарантирует, что нашел кратчайший путь.
Есть множество алгоритмов, похожих на сортировку слиянием Джона фон Неймана или нахождение кратчайшего пути. Вот несколько примеров: алгоритм Краскала для нахождения минимального остовного дерева (например, схема кратчайшей железнодорожной сети, соединяющей все города страны); расстояние Хэмминга для обнаружения разницы между двумя частями текста или данных; алгоритмы построения выпуклой оболочки для изображения фигуры, окружающей некоторое множество точек; алгоритмы обнаружения столкновения в 3D-графике; быстрое преобразование Фурье для обнаружения сигнала. Эти алгоритмы и их вариации – строительные блоки для аппаратного и программного обеспечения компьютеров. Они сортируют и обрабатывают наши данные, перемещают электронные письма, проверяют грамматику и позволяют Сири или Алексе за секунды идентифицировать передаваемую по радио песню.
Математика «Если… то…» всегда дает правильный ответ, и мы всегда знаем, что делать дальше. Возьмите, например, футбольного бота, созданного тремя студентами магистратуры. Я мог задавать ему простые вопросы о футболе, он отвечал; но Антона его ответы не удивляли. Антон закодировал правила, которые определяют, что говорит бот, и программа четко следует им.
Почему я свалил в одно общее уравнение все алгоритмы «если… то…»? Потому что у них есть одно очень важное общее свойство: они универсальные истины. Алгоритм Дейкстры всегда найдет кратчайший путь; сортировка слиянием всегда отсортирует список имен от A до Z; выпуклая оболочка для множества точек всегда имеет одну и ту же конструкцию. Это утверждения, которые истинны независимо от того, что мы говорим или делаем.
В первых девяти главах этой книги мы использовали уравнения для проверки моделей, составления прогнозов и оттачивания нашего понимания реальности. Эти уравнения взаимодействуют с миром: мы позволяем прошлым данным информировать наши модели, а те прогнозируют будущие данные. Но алгоритмы «если… то…» негибкие. Они берут данные – скажем, список имен для сортировки или список точек, между которыми можно вычислить кратчайший путь, – и выдают ответ. Мы не пересматриваем свое знание мира на основе полученных ответов. Точно так же и наши наблюдения не влияют на истинность алгоритмов. Вот почему я называю их универсальными: их истинность доказана, они работают всегда.
Вышеприведенные примеры – алгоритмы из программирования, однако другие математические утверждения-теоремы из геометрии, анализа и алгебры также универсальные истины. В мы видели пример парадокса дружбы. Сначала кажется невероятным, что наши друзья в среднем популярнее нас, но с помощью логических рассуждений мы показали, что это верно и иначе быть не может.
Математика полна удивительных результатов, которые сначала могут противоречить интуиции. Например, тождество Эйлера (названное в честь великого математика Леонарда Эйлера) eπi + 1 = 0 говорит нам о связи между тремя хорошо известными величинами, основанием натуральных логарифмов e = 2,71828…, π = 3,14159… и i = √–1. Этот факт так изящно сочетает фундаментальные константы, что его называют самой красивой формулой в математике.
Еще один пример – золотое сечение:
φ = (1 + √5) / 2 = 1,618…
Это число появляется, когда мы рисуем прямоугольник, который можно разрезать на квадрат и новый прямоугольник, подобный исходному. Иными словами, если сторона этого квадрата равна a, а стороны прямоугольника – a и b, то прямоугольник называется золотым, когда
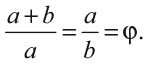
Интересно, что число φ (фи) также появляется в связи с последовательностью чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34…, которая получается, когда мы складываем два предыдущих числа для получения следующего (1 + 1 = 2, 1 + 2 = 3 и т. д.). Если мы рассмотрим отношение двух последовательных чисел Фибоначчи, то оно будет все сильнее приближаться к числу φ (например, 13/8 = 1,625, 21/13 = 1,615…, 34/21 = 1,619… и т. д.). Эти два примера – всего лишь начальная точка для путешествия в чистую математику, где повседневная интуиция начинает подводить и только строгие логические рассуждения могут вести вперед.
Огромное количество математических теорем, оказавшихся истинными, побудило французского математика Анри Пуанкаре написать в своей книге 1902 года «Наука и гипотеза»: «Если все предложения, которые математика выдвигает, можно вывести друг из друга по правилам формальной логики, то каким образом математика не сводится к бесконечной тавтологии? Логический вывод не может нас научить ничему существенно новому… Неужели мы можем допустить, что все эти теоремы, которые заполняют столько томов, нужны только для того, чтобы окольным способом сказать, что А есть А?» Вопрос Пуанкаре был риторическим, поскольку он считал, что проблемы, с которыми он и другие люди сталкиваются при разгадывании математических истин, должны содержать нечто более глубокое, нежели просто логические утверждения.
Аналогичная точка зрения в книге Дэна Брауна «Код да Винчи» – оригинальной, хотя и вымышленной теории математического заговора. В книге профессор Лэнгдон говорит: «Когда древние открыли число фи [φ], они были уверены, что наткнулись на строительный блок, который Бог использовал при создании мира… Загадочное волшебство, присущее божественной пропорции, было написано в начале времен». Лэнгдон переходит к примерам (некоторые верны, некоторые нет), как золотое сечение, которое он называет божественной пропорцией, можно увидеть в биологии, искусстве и культуре. На протяжении всей истории участники «Десятки» использовали φ в качестве кода, причем имя одного из главных персонажей романа – СоФИ Невё – содержало ключ.
Должен признать, что этот аспект математики меня очень привлекает. Я наслаждался «Кодом да Винчи». Есть что-то невероятное в обнаруживаемых нами неожиданных связях – не только в числах вроде фи, но и в алгоритме Дейкстры для кратчайшего пути, и в сортировке слиянием фон Неймана. Такая простая элегантность кажется выходящей за рамки обыденной реальности. Может, за всеми этими уравнениями скрыт какой-то глубокий код?
Правильный ответ на вопрос Пуанкаре гораздо более незатейлив и прямолинеен, чем он ожидал: «да». Все великие теоремы математики, как и все алгоритмы сортировки и организации из информатики, говорят всего лишь, что А равно А. Все они представляют собой одну колоссальную тавтологию; это очень полезные и неожиданные тавтологии, но тем не менее тавтологии. Пуанкаре был прав буквально и неправ риторически.
Рассуждение, которое утверждает, что Пуанкаре был прав, можно найти в книге «Язык, истина и логика». В ней Айер использовал пример с треугольником. Представьте, что друг рассказывает вам о треугольнике, у которого сумма углов меньше 180 градусов. У вас есть два способа отреагировать: либо сказать ему, что он измерил неправильно, либо сообщить, что объект, который он имеет в виду, не треугольник. Ни при каких обстоятельствах вы не измените своего мнения о математических свойствах треугольника на основании данных вашего друга. Он не найдет в реальном мире треугольника, подрывающего устои геометрии.
И не существует списка слов любого языка, который невозможно отсортировать по алфавиту. Если я покажу вам список, где Айер стоит после Самптера, и скажу, что это – результат сортировки слиянием, то вы скажете, что либо мой алгоритм не работает, либо я не знаю алфавита. Он точно не станет доказательством, что сортировка слиянием не работает. Аналогично не существует компьютерной сети, в которой кратчайший путь длиннее, чем второй, по краткости.
К сожалению для профессора Лэнгдона, причина появления числа φ = 1,618… во всех этих геометрических и математических соотношениях состоит в том, что оно являет собой положительный корень квадратного уравнения x2 – x – 1 = 0. И изучение последовательности Фибоначчи, и нахождение золотого сечения приводят к решению одного и того же квадратного уравнения, поэтому дают один и тот же ответ. Нет никакого загадочного магического кода, скрытого в числе фи или в любом другом.
Точка зрения Айера: математические теоремы не зависят от данных. Математика непроверяема. Она состоит из тавтологических утверждений, которые можно доказать с помощью логики, но сами по себе они ничего не говорят о реальности. В ответ на риторический тон Пуанкаре Айер писал: «Способность логики и математики удивлять нас, как и ее полезность, зависит от ограниченности нашего разума».
Пуанкаре вводил в заблуждение тот факт, что заниматься математикой порой трудно даже ему. По сути, математические результаты не зависят от наших наблюдений. Вот почему я говорю, что они универсальны. Они верны для всей Вселенной – независимо от того, что мы говорим и делаем, от научных открытий, от того, сделал их Пуанкаре или другой математик.
Как мы видели в этой книге, сила десяти уравнений в том, что они взаимодействуют с реальным миром, комбинируя модели и данные. В отрыве от данных уравнения не имеют глубокого смысла. Они определенно не несут нам какой-то морали и не имеют ничего общего с Богом. Это просто набор крайне полезных результатов, которые оказались истинными.
Чтобы найти загадку и мораль в математике, нам придется поискать не в самих теориях, а в других местах.
* * *
Я все откладывал звонок Мариусу. Ян попросил, чтобы я позвонил и все уточнил у него, прежде чем публиковать финансовые подробности их операции со ставками, и я несколько опасался, что Мариус может ответить отказом. Возможно, ему хочется хранить все это в тайне от любопытных глаз.
Я напрасно беспокоился. Мариус был рад поговорить и выложил мне все подробности. Их прибыли продолжали расти, хотя ему приходилось сложно.
– Если изо дня в день смотреть на цифры, можно сойти с ума, – сказал он.
В какой-то момент у них был неудачный период, когда друзья потеряли 40 тысяч долларов.
– Это был худший момент за все время. Ты реально начинаешь сомневаться. Но мы продолжили работать и не торопились. И числа снова поднялись. Потом опять упали… и поднялись.
Мариус сказал, что азартные игры научили его быть более терпеливым и концентрироваться на вещах, которые он может изменить.
– Мы не можем управлять колебаниями. Я научился не смотреть матчи, как во время чемпионата мира. Сначала я проверял наши ставки в режиме реального времени. Сейчас просто прихожу в офис и работаю, а обзор мы смотрим раз в квартал.
– Вы когда-нибудь задумывались о моральной стороне того, что делаете? – спросил я. – О людях, которые теряют, когда вы выигрываете?
– Я думаю, что азартные игры – щекотливый вопрос из-за всей этой рекламы, которая обманывает, – ответил Мариус. – Но в то же время всего лишь быстрый поиск в Сети по разным ставкам даст вам все, что нужно, чтобы оставаться в плюсе как любителю. Просто люди не хотят себя утруждать.
Он был прав. Это моральный урок из уравнения ставок. Если люди не хотят потратить несколько часов на поиск информации в интернете – почему Мариус должен за это отвечать? Мариус и Ян создали сайт, содержащий именно ту информацию, которая нужна этим людям для ставок у мягких букмекеров. Но очень мало кто делает ставки так, как они.
Я спросил Мариуса, что он будет делать, если рынки изменятся внезапно и он все потеряет.
– Никогда не знаешь, как все обернется. Такое всегда возможно, – ответил Мариус. – Но мне очень нравится то, что я делаю, и именно поэтому я счастлив. Мне не хотелось бы сидеть на пляже, пока какой-нибудь бот работает. Мне интересно копаться в данных и извлекать что-то оттуда.
Он обнаружил настоящий секрет «Десятки», и тот имел мало общего с количеством денег на его банковском счете. Его вознаграждением было количество новых знаний.
Можно ли это считать признаком морали? Думаю, да. Я считаю, что в подходе Яна и Мариуса есть интеллектуальная честность. Они не лгут о своих действиях. Они играют в игру по имеющимся правилам и выигрывают, потому что у них это получается лучше. То же можно сказать об операциях со ставками Уильяма Бентера и Мэттью Бенхэма в более крупном масштабе. Честность Бентера была поразительной. Все считали, что он остерегается раскрыть, сколько и где выиграл, однако он опубликовал статью о своих методах в научном журнале. Любой человек с математическими умениями сейчас может взять методы Бентера и применить их на практике.
Те, кто много работает, учится и проявляет настойчивость, – победители. Те, кто срезает углы, проигрывают. То же правило применимо ко всей «Десятке». Если выносим суждения, то вынуждены говорить, как данные сформировали наши убеждения. Когда строим модель умений, должны формулировать свои предположения. Когда инвестируем или делаем ставку – признаём свои прибыли и убытки, чтобы улучшить свою модель. Мы должны сообщать друг другу, насколько уверены в своих выводах. Мы вынуждены признаться, что не мы центр нашей социальной группы, и нам не стоит жалеть, что мы не самые популярные. Когда мы видим какую-то корреляцию, вынуждены искать причинно-следственную связь. Когда создаем технологию, нам демонстрируют, как она вознаграждает и наказывает людей, которые ею пользуются. Такова суровая мораль математики. В итоге истина всегда побеждает.
Участники «Десятки» – настоящие защитники интеллектуальной честности. Они излагают свои предположения, собирают данные и сообщают ответы. Когда они не знают полного ответа, то говорят нам, чего не хватает. Они перечисляют правдоподобные альтернативы и указывают вероятность каждой из них; они начинают думать о следующих шагах, которые можно предпринять, чтобы узнать больше.
Верните честность в свою жизнь. Десять уравнений вам в помощь. Начните с размышлений о вероятностях – и с точки зрения азартных игр, когда вы стремитесь получить желаемое, и с точки зрения понимания риска неудачи. Прежде чем делать выводы, улучшайте свои суждения, собирая данные. Повышайте свою уверенность, не убеждая себя в своей правоте, а крутя колесо много раз. Каждый урок, которому учат нас уравнения – от обнаружения фильтра, созданного нашей социальной группой, до понимания того, как социальные сети ведут нас к критической точке, – снова и снова напоминает о важности честного подхода к модели и использования данных для улучшения нас самих.
Если вы будете следовать этим уравнениям, то заметите, как окружающие начнут уважать ваши суждения и ваше терпение. Это первый смысл, в котором математика может быть источником морали. Она сообщает нам суровые истины о нас и о людях вокруг.
* * *
В биографии Алфреда Айера, написанной Беном Роджерсом, излагается история о встрече философа с боксером Майком Тайсоном в 1987 году. Айер, которому тогда было семьдесят семь, находился на вечеринке на 57-й улице на Манхэттене, когда в комнату вбежала какая-то женщина со словами, что в спальне набросились на ее подругу. Айер обнаружил, что Тайсон пытался приставать к молодой Наоми Кэмпбелл (будущей супермодели).
Роджерс пишет, что Айер сказал Тайсону прекратить. Боксер ответил:
– Черт возьми, ты знаешь, кто я? Чемпион мира в тяжелом весе.
Айер стоял на своем.
– А я бывший профессор логики в Оксфорде. В своих областях мы оба знамениты. Предлагаю поговорить об этом как разумные люди.
Тайсон, который, видимо, оказался любителем философии, был достаточно впечатлен и отступил.
Впрочем, если бы Тайсон захотел ударить Айера интеллектуальным апперкотом, он мог бы спросить его, на каком основании философ считает оправданным вмешиваться в его заигрывания с Наоми Кэмпбелл. В конце концов, как утверждал сам Айер в книге «Язык, истина и логика», мораль лежит вне рамок эмпирической дискуссии. Хотя вполне могло быть так, что Кэмпбелл боялась Тайсона. Железный Майк мог спросить: «Существуют ли логические причины, по которым мужчинам ненормально навязывать себя женщинам при их собственном сексуальном влечении?»
Айеру пришлось бы признать, что он навязывает общепринятые нормы того типа собраний, на котором они присутствовали в данный момент. К этому Тайсон мог бы добавить, что его нормы, приобретенные в криминальной юности на улицах Бруклина, отличались от норм Айера, получившего образование в Итоне; а это оставляло им мало общих позиций для продолжения дискуссии. «И если вы не возражаете, – мог бы продолжить Железный Майк, – то я хотел бы вернуться к ухаживанию за этой красивой дамой тем способом, который считаю наиболее подходящим».
Не могу знать, в этом ли направлении шел их разговор, но точно известно, что во время их беседы Наоми Кэмпбелл сбежала с вечеринки. Майка осудили за изнасилование другой женщины спустя четыре года, и теперь он сексуальный преступник.
Эта история Тайсона и Айера иллюстрирует (среди прочего) фундаментальную проблему для любого последователя строго позитивистского подхода. Невозможно решить даже самые очевидные моральные дилеммы. Несмотря на честность математики и логического мышления, каждый человек должен сам разбираться со своей нравственностью.
Очевидно, здесь в логическом позитивизме чего-то не хватает. Вопрос – чего? Чтобы отточить наши представления о роли математики в морали, английский философ Филиппа Фут разработала в 1967 году мысленный эксперимент, который стал известным под названием «проблема вагонетки». Его можно описать так:
Эдвард управляет вагонеткой, у которой отказали тормоза. На рельсах перед ним пять человек, и насыпи настолько крутые, что люди не успеют сойти с пути. У рельсов есть ответвление вправо, и Эдвард может повернуть вагонетку туда. К сожалению, на правом пути тоже есть человек. Эдвард может либо повернуть вагонетку и убить одного человека, либо не поворачивать и убить пятерых.
Встает вопрос – что делать Эдварду: повернуть и убить одного либо ехать прямо и убить пятерых. Немного поразмыслив, большинство из нас обычно решают, что первый вариант лучше. Одно убийство лучше, чем пять. Пока все хорошо.
Теперь рассмотрим другой вариант проблемы вагонетки, предложенный в 1976 году Джудит Томсон – профессором философии из Массачусетского технологического института:
Джордж стоит на пешеходном мостике над рельсами для вагонетки. Они видит, что одна вагонетка приближается, а за мостом на рельсах стоят пять человек, и насыпи настолько крутые, что люди не успеют сойти с пути. Джордж понимает, что есть один способ остановить неуправляемую вагонетку: сбросить перед ней что-нибудь тяжелое на рельсы. Однако единственный имеющийся достаточно тяжелый объект – какой-то толстяк, который тоже смотрит на вагонетку с моста. Джордж может либо столкнуть его на рельсы перед вагонеткой, убив его при этом; либо не делать этого и позволить умереть пятерым.
Что делать Джорджу? С одной стороны, сбрасывать человека на рельсы явно неправильно. С другой – при бездействии он позволяет погибнуть пяти человекам (как если бы Эдвард не повернул вагонетку).
В опросе примерно 81 % американцев сказали, что на месте Эдварда отклонили бы вагонетку и убили одного человека; однако всего 39 % считали, что Джорджу нужно столкнуть толстяка и спасти пятерых. Китайские и российские респонденты также были более склонны полагать, что Эдварду нужно действовать, а Джорджу – нет. Это поддерживает гипотезу, что у людей есть общее моральное представление для таких дилемм. Однако культурные различия всё же имеются: китайцы скорее позволят вагонетке двигаться своим курсом в обеих ситуациях.
Джудит Томсон разработала этот второй вариант проблемы вагонетки, чтобы дилемма стала прозрачной. Обе проблемы описывают одну математическую задачу – спасти пятерых или спасти одного; однако наша интуиция говорит, что они сильно отличаются друг от друга. Математическое решение простое – моральное гораздо сложнее. Проблемы вагонетки заставляют нас задуматься о действиях, которые мы готовы – или не готовы – предпринять для спасения жизней.
Проблема вагонетки лежит в центре многих произведений современной научной фантастики. Эта дилемма занимает от тридцати минут до часа в фильме (внимание: спойлер) «Мстители: война бесконечности» из вселенной Marvel. Философски настроенный суперзлодей Танос, став свидетелем того, как перенаселение полностью разрушило его родную планету, решает, что неплохо бы уничтожить половину населения вселенной. Он считает, что убийство половины людей сейчас спасет больше жизней в будущем, и – если рассуждать в терминах задачи Томсон – решает щелчком пальца сбросить миллиарды толстяков под вагонетку. В продолжении – «Мстители: финал» – Тони Старк сталкивается с более личной дилеммой того же типа: существование его дочери или возвращение друзей. Его просят сделать практически невозможный выбор.
Обычно в научной фантастике злодеи предпочитают столкнуть толстяка. Во многих случаях такое решение изображается в форме жесткой беспощадной логики. Роботы или ИИ принимают утилитарное решение спасти пятерых, а не одного – независимо от того, насколько ужасно действие, необходимое для достижения их цели. Для прагматичного робота, запрограммированного людьми на спасение максимального количества людей, в приоритете числа, а не чувства. При прочих равных условиях пользы от пятерых больше, чем от одного. Это точно тот же вопрос, который Филиппа Фут и Джудит Томсон иллюстрировали проблемой вагонетки: неверно считать, что мы можем решить такие проблемы с помощью утилитарного подхода. В фильмах роботы ошибаются, а если бы существовали в реальной жизни – ошибались бы тоже. Научная фантастика напоминает нам, что мы не можем создать универсальное правило, например
если 5 > 1, то печатать («спасти 5»),
чтобы решить все проблемы. Если мы так сделаем, то совершим самые ужасные моральные преступления, которые никогда не сможем оправдать перед будущими поколениями.
Когда я был моложе, мог смотреть на отказ от действия – даже сталкивания толстяка на рельсы – как на указание логической слабости части человечества.
С моей стороны это было ошибкой, и не только потому, что я оказался слишком строг к человечеству. По сути, делать такой вывод – логическая слабость. Проблема вагонетки иллюстрирует два момента. Во-первых, она подтверждает, что на вопросы реальной жизни нет чисто математических ответов. Это то же, что Айер отвечал на риторический вопрос Пуанкаре об «универсальной» природе математики. Это причина того, что кода да Винчи не существует. Наше ощущение универсальности математики – результат ее тавтологической природы, а не более глубокой истинности. Мы не можем использовать ее как божественные заповеди. Только – как в этой книге – в качестве инструмента для организации своей работы вокруг моделей и данных.
Во-вторых, дилемма вагонетки сообщает нам, что чистый утилитаризм – идея, что мораль можно построить вокруг попытки максимизировать счастье, жизнь или любую другую переменную – одно из величайших зол среди всех (одинаково неверных) моральных кодексов, доступных нам. Правило «спасти как можно больше жизней» противоречит нашей нравственной интуиции и заставляет нас делать ужасные вещи. Если мы начинаем разрабатывать оптимальные моральные кодексы, то в итоге создаем моральный лабиринт.
Я пришел к выводу, что на эти дилеммы есть очень простой ответ: мы должны научиться доверять своей нравственной интуиции и пользоваться ею. Это и сделал Алфред Айер при стычке с Майком Тайсоном. То же сделала Моа Бёрселл, когда решила изучать расизм, увидев, как нацисты преследуют ее друзей. Это то, чем руководствовался я, когда изучал дела компании Cambridge Analytica, фейковые новости и предвзятость алгоритмов или руководил написанием диссертации Бьорна по иммиграции и подъеме правых сил в Швеции. Это то, чем руководствовалась Николь Нисбетт, когда рассматривала коммуникацию в политике. И именно это делает Человек-паук: с помощью своей интуиции и умений убивает плохого парня.
Проблема вагонетки говорит нам, что нужен более мягкий способ размышлений для таких моральных и философских дилемм – дополняющий жесткую брутальную честность использования моделей и данных.
Участники «Десятки», которые вносят наибольший вклад в общество, мыслят и мягко (используя свою нравственную интуицию, чтобы определить, какие проблемы им решать), и жестко (сочетая модели и данные ради честности своих ответов). Они прислушались и поняли ценность окружающих. Они осознают, что не более любого другого человека компетентны, чтобы выбирать проблемы, но более компетентны в умении их решать. Они служители общества, сохранившие тот дух, что ввел в «Десятку» Ричард Прайс почти 260 лет назад. Прайс был неправ насчет чудес, но верно указал на необходимость нравственности, когда мы применяем математику.
У меня нет убедительных доказательств, но я полагаю, что после того, как логический позитивизм отбрасывает идею универсального утилитаризма, у нас остается направляющая нас моральная интуиция. Именно этот мягкий способ мышления говорит нам, какие проблемы нужно решать.
* * *
Участникам «Десятки» нужно разговаривать, учиться справляться с силой, нам данной, – точно так же, как Человек-паук осознаёт свои слабости в каждом новом воплощении.
Быть мягким означает, что бездумно приумножать деньги невежественных банкиров, занимающихся инвестициями, ненормально. Это значит, что нам не следует патентовать основные уравнения, чтобы зарабатывать деньги. Мы должны продолжать открыто рассказывать об используемых алгоритмах, делиться всеми своими секретами с теми, кто готов потрудиться, изучая их.
Мы должны использовать свою интуицию, чтобы двигаться к важным вопросам. Нам стоит прислушиваться к чувствам других людей и выяснять, что для них важно. Многие из нас уже делают это, но нам нужно быть открытыми в отношении того, кто мы есть и почему делаем то, что делаем.
Нам надо быть мягкими при определении своих проблем и жесткими в их решении.
* * *
Я сижу в комнате для семинаров на цокольном этаже математического факультета одного из университетов на севере Англии. Перед нами Виктория Спейсер, политолог из Лидского университета; она представляет сегодняшних докладчиков. Вместе со своим коллегой по исследованиям и спутником жизни Ричардом Манном она организовала двухдневный семинар об использовании математики в сфере гражданской активности. Цель – свести вместе математиков, специалистов по данным, представителей власти и бизнеса и найти способы использования математических моделей, чтобы сделать мир лучше.
Впервые я встретил Викторию почти восемь лет назад, Ричарда – чуть раньше. Вместе еще с одним моим аспирантом – Шьямом Ранганатаном – мы работали над моделированием расовой сегрегации в школах Швеции, демократических преобразований в странах мира и разработкой методов, с помощью которых ООН может достичь своих зачастую противоречивых целей устойчивого развития. Мы не всегда говорили об этом вслух, но всегда втайне считали, что математика должна не просто изучать мир, а менять его к лучшему. Выбор слова «активность» в названии собрания – наша первая попытка открыто заявить о наших целях.
Мы не одиноки. После того как Виктория открывает семинар, участники встают один за другим и говорят, чем они занимаются. Адам Хилл из британской компании DataKind создал сеть, показывающую связи между людьми, сидящими в правлениях анонимных компаний, которые созданы в Великобритании для сокрытия владения. Сопоставляя права собственности, он и его команда могут обнаружить коррупцию и потенциальное отмывание денег. Бетти Наньонга из Уганды рассказала нам, как ее коллеги используют математические модели, чтобы понять причины студенческих забастовок в Университете Макерере, Кампала, где она работает. Анна Оуэн, научный сотрудник Лидского университета, показала, что Грета Тунберг была права, когда заявила, что Великобритания лгала, говоря о сокращениях выбросов CO2. Анна демонстрирует нам правильный расчет, учитывающий производство и транспортировку всех пластиковых товаров, которые мы импортируем из Китая. Среднестатистический человек в возрасте 60–69 лет – летая в отпуск или управляя большой машиной – создает в год на 64 % больше выбросов СО2, чем молодой человек до 30 лет. Именно старшее поколение, некоторые представители которого критикуют Грету Тунберг, должно тщательнее всего думать об углеродных выбросах.
Возможно, вы не знали о нас до сих пор, но теперь знаете.
Секрет раскрыт. «Десятка» – это мы.
Назад: Глава 9. Уравнение обучения
Дальше: Благодарности

