В предыдущем разделе мы написали, что средний рост женщины составляет 5 футов 4 дюйма. Если вам нужно угадать рост случайного незнакомца, но вы не знаете наверняка, что это женщина, не стоит называть 5 футов 4 дюйма, потому что средний мужской рост ближе к 5 футам 9 дюймам (175 см) и лучше брать число ближе к середине. Но если у вас есть дополнительная информация о том, что этот человек – женщина, то 5 футов 4 дюйма – это самая удачная догадка. Дополнительные данные влияют на вероятность.

Это пример модели, которая называется условной вероятностью – вероятностью наступления одного события при условии, что другое событие уже произошло. Условная вероятность помогает лучше оценивать вероятности, используя дополнительную информацию.

Условные вероятности широко распространены в повседневной жизни. Например, тарифы страхования жилья привязаны к различным условиям вероятности страховых требований (например, на побережье Флориды надбавки выше, так как и угроза разрушения от урагана там выше, чем в Пенсильвании). Точно так же генетическое тестирование скажет вам, подвержены ли вы повышенному риску определенных заболеваний: женщины с аномалиями генов BRCA1 или BRCA2 имеют до 80 % больше риска развития рака груди в возрасте девяноста лет.

Условная вероятность обозначается символом |. Например, вероятность (Р), что у вас будет рак груди к девяноста годам при условии, что вы женщина с мутацией гена BRCA, будет обозначаться как Р (рак груди в 90 лет | женщина с мутацией BRCA).

Некоторых сбивает с толку условная вероятность. Они путают вероятность того, что событие А произойдет при условии, что произошло событие В – Р(А|В), – с вероятностью того, что событие В произойдет при условии, что произошло событие А – Р(В|А). Это называется обратной ошибкой. Вы только что видели, что Р (рак груди в 90 лет | женщина с мутацией BRCA) составляет около 80 %, но вероятность Р (женщина с мутацией BRCA | рак груди в 90 лет) составляет всего 5–10 %, поскольку рак груди развивается у многих других людей без этой мутации.

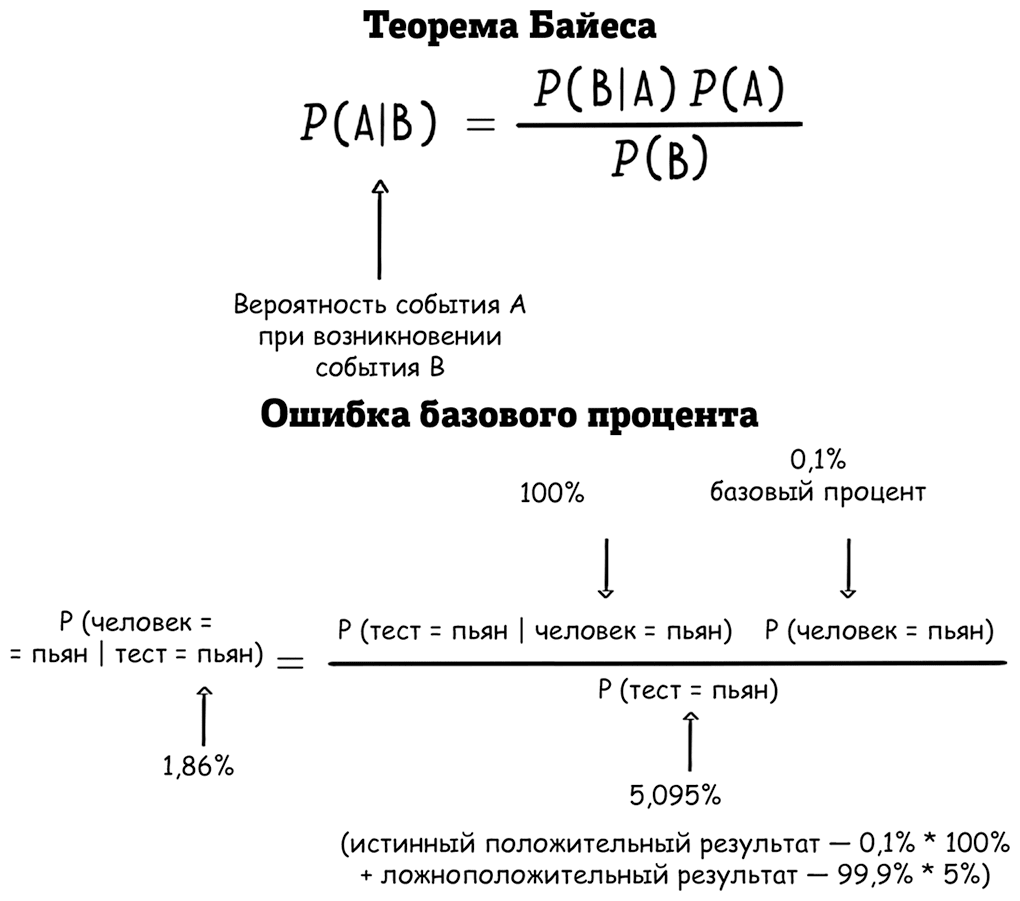
Разберем более длинный пример, чтобы посмотреть на эту ошибку в действии. Допустим, полиция останавливает произвольного водителя, чтобы проверить на алкоголь, и заставляет его подышать в трубочку. Кроме того, предположим, что тест выдает ошибку примерно в 5 % случаев, показывая, что трезвый человек пьян. Какова вероятность, что этого человека несправедливо обвинят за вождение в нетрезвом виде?

Скорее всего, вы первым делом назовете 5 %. Однако вам дана вероятность, что тест объявляет человека пьяным, даже если на самом деле он трезв, то есть Р (тест = пьян | человек = трезв) = 5 %. Но что, если вас спросят, какова вероятность того, что человек трезв, если тест говорит, что он пьян, или Р (человек = трезв | тест = пьян)? Это совсем другая вероятность!

Вы не учли зависимость результата от базового процента пьяных за рулем. Представьте сценарий, где все ведут себя правильно и никто никогда не садится за руль пьяным. В таком случае вероятность, что человек трезв, будет 100 %, независимо от того, что покажет алкотестер. Когда при расчете вероятности не учитывается базовый процент (например, базовый процент числа пьяных водителей), такая ошибка называется ошибкой базового процента.

Представим себе более реалистичный базовый процент, когда пьян 1 водитель из 1000. Значит, есть маленький шанс (0,1 %), что человек, которого случайно остановила полиция, пьян. А так как мы знаем, что один из 20 тестов выдает ошибку (ошибка возникает в 5 % случаев), полиция, скорее всего, сделает очень много ошибок, прежде чем действительно поймает пьяного за рулем.

На самом деле, если полиция остановит тысячу человек, в среднем они проведут около 50 ошибочных тестов, пытаясь найти одного по-настоящему нетрезвого водителя. Таким образом, вероятность ошибки алкотестера составляет всего 2 %, то есть аппарат ошибочно показывает, что человек пьян. Или можно заявить, что трезвые водители попадаются в 98 % случаев. А это намного, намного больше, чем 5 %!

Итак, Р(А|В) не равно Р(В|А), но как же они связаны? Существует очень полезная теорема Байеса, которая показывает взаимосвязь между этими двумя условными вероятностями. Вот как на примере нетрезвого вождения можно применить теорему Байеса, чтобы вычислить результат в 2 %.

Теперь, когда вы знаете о теореме Байеса, вы также должны знать, что в статистике есть две школы, основанные на разных представлениях о вероятности: частотная и байесовская. Большинство исследований, о которых вы слышите в новостях, основаны на частотной статистике, которая требует и опирается на множество наблюдений за событием, прежде чем сделать надежные статистические выводы. Частотники считают, что вероятность фундаментально связана с частотой возникновения событий.

Наблюдая частоту результатов в большой выборке (например, спрашивая большое количество людей, одобряют ли они Конгресс), частотники вычисляют неизвестное количество. Но если точек ввода данных очень мало, они ничего не могут сказать по существу, потому что доверительные интервалы, которые они вычислят, будут очень большими. С их точки зрения, вероятность без наблюдений не имеет смысла.

Напротив, байесовцы позволяют себе вероятностные суждения о любой ситуации, независимо от того, были ли какие-либо наблюдения. Для этого они начинают с приведения соответствующих данных к статистическим определениям. Например, подбирая монетку на улице, изначально вы, вероятно, решите, что шансы выбросить решку составляют 50/50, даже если никогда раньше не видели, чтобы эту монетку подбрасывали. В байесовской статистике можно учесть в задаче такое знание базовых процентов. А в частотной статистике так сделать нельзя.

Многие люди считают байесовский взгляд на вероятность более интуитивным, потому что он похож на естественное развитие ваших убеждений. В повседневной жизни вы не начинаете каждый раз с нуля, как частотники. Например, в вопросах политики отправная точка – это ваши знания по определенному вопросу (байесовцы зовут это априори), но получив новые данные, вы (будем надеяться) обновите свое априори на их основании. То же самое верно для отношений, когда начальная точка для вас – это пережитый вами опыт с определенным человеком. Сильное априори – это отношения на всю жизнь, а слабое – только первое впечатление.

В предыдущем разделе вы видели, как частотная статистика производит доверительные интервалы. Такая статистика говорит вам, что, если провести эксперимент множество раз (например, подбросить монетку сто раз), вычисленные доверительные интервалы будут содержать изучаемый параметр (например, 50 % вероятность выбросить решку) до указанного уровня доверия (например, 95 % раз). К большому разочарованию многих, доверительный интервал не сообщает, что есть 95 % вероятность получить истинное значение параметра в этом интервале. Напротив, байесовская статистика аналогичным образом производит байесовские доверительные интервалы, которые это сообщают. Они указывают текущий наилучший оценочный диапазон для вероятности параметра. Таким образом, байесовский подход снова оказывается более интуитивным.

На практике оба подхода дают очень похожие результаты и по мере поступления данных должны сходиться к одному и тому же выводу. Ведь они оба пытаются найти одну и ту же основную истину. Исторически точка зрения частотников была популярнее, во многом потому, что байесовский анализ часто бывает затруднительным из-за громадного объема вычислений. Хотя нынешние вычислительные машины легко с этим справляются.

Байесовцы уверены, что с сильным априори они начинают ближе к истине и быстрее достигают конечного результата с меньшим числом наблюдений. Поскольку наблюдения требуют денег и времени, это привлекательно. Но есть и обратная сторона: возможно, байесовские априори на самом деле делают обратное – заставляют начинать дальше от истины. Такое происходит, если это сильные убеждения на основе искажения подтверждения (см. главу 1) или другой когнитивной ошибки (например, неоправданно сильного априори). В таком случае байесовский подход будет искать истину дольше, так как точка зрения частотников (с нуля) ближе к истине с самого начала.

Можно сделать вывод, что есть два подхода к статистике и они оба верны, если все делать правильно. Некоторые люди являются убежденными идеологами, которые клянутся в верности одной философии или другой, тогда как прагматики (вроде нас) используют те методы, которые лучше всего подходят для ситуации. Помните, что нельзя допускать путаницы между условной вероятностью и ее обратным значением: P(A|B) не равно P(B|A). Теперь вы знаете, что эти вероятности связаны теоремой Байеса, которая учитывает соответствующие базовые проценты.