Глава 13. Эпоха алгоритмов

В июне 2016 года я был в Сингапуре, где в Наньянском технологическом университете в течение недели проходило обсуждение «Фундаментальные проблемы науки». Темы дискуссий были самыми разными: от космологии и эволюции до государственной политики в отношении науки. Брайан Артур – экономист, сильно интересующийся информационными технологиями, – говорил об алгоритмах. Он отметил, что в прошлом технологии основывались на законах физики, которые описывались дифференциальными уравнениями. В XX веке мы добились глубокого понимания физического мира, используя уравнения и математику непрерывных переменных как главный источник идей. Непрерывная переменная плавно изменяется во времени и пространстве. Однако в основе технологий сегодняшнего дня лежат алгоритмы. В XXI веке мы успешно постигаем природу сложности в компьютерных науках и биологии с помощью дискретной математики и алгоритмов. Артур преподает в Институте Санта-Фе в Нью-Мексико – одном из многих центров, возникших в XX веке для исследования сложных систем.

Алгоритмы окружают нас. Вы используете алгоритмы каждый раз, когда что-то гуглите. Новости, которые вы читаете в ленте новостей Facebook, выбираются по алгоритму, основанному на истории ваших просмотров, что влияет на ваш эмоциональный отклик. Алгоритмы внедряются в вашу жизнь все быстрее, поскольку глубокое обучение дает вашему смартфону возможность распознавать речь и естественный язык.

Что такое алгоритм? Алгоритм – это процесс, выполняющийся шаг за шагом, или набор правил, которым необходимо следовать при выполнении расчетов или решении задачи. Слово «алгоритм» происходит от латинского algorismus, составленного из имени Аль-Хорезми, персидского математика IX века, и греческого слова arithmos – «число». Хотя алгоритмы зародились очень давно, цифровые компьютеры выдвинули их на передний план науки и техники.

Сложные системы

В 1980-х годах случился расцвет новых подходов к сложным системам. Целью была разработка современных способов изучения систем, как те, что мы видим в природе сложнее, чем физика и химия. То, как летит ракета, несложно объяснить законами Ньютона, но не было простого способа описать дерево или то, как оно растет. Первопроходцы в области ИИ использовали компьютерные алгоритмы для изучения извечных вопросов о живых существах.

Рис. 13.1. Стивен Вольфрам у себя дома в Конкорде в штате Массачусетс стоит на полу, который сгенерировал алгоритм. Вольфрам – один из родоначальников теории сложности, и он показал, что даже простые программы могут создавать сложность подобно тем, с которыми мы сталкиваемся в реальном мире

Стюарт Кауфман получил медицинское образование, и его сильно заинтересовали генетические сети, в которых белки, называемые факторами транскрипции, могут нацеливаться на гены и влиять на их активацию. Его модели были самоорганизующимися и основывались на сетях из двоичных единиц, схожих с нейронными сетями, но намного медленнее. Крис Лэнгтон ввел термин «искусственная жизнь» в конце 1980-х годов, что привело к неоднократным попыткам понять принципы, которые лежат в основе сложности живых клеток и развития сложных форм поведения. Несмотря на прогресс, тайна жизни продолжает ускользать от нас. Между тем клеточная биология и молекулярная генетика выявили высокую сложность молекулярных механизмов внутри клеток.

Блок 7. Клеточный автомат

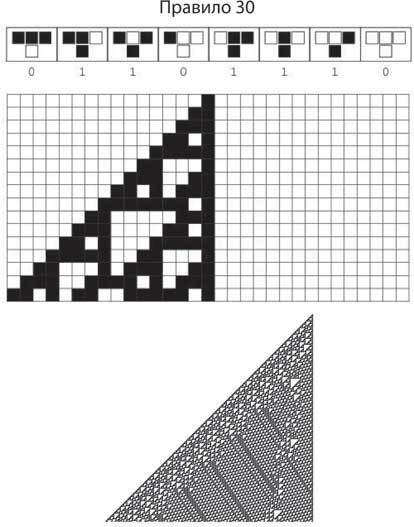
Правило клеточных автоматов определяет цвет ячейки в зависимости от ее цвета и цвета ближайших ячеек. Например, для восьми возможных комбинаций черного и белого для трех ячеек в верхнем ряду, правило 30 указывает следующий цвет под ними. Эволюция этого правила, применяемого к одной строке за раз, начиная с одиночной черной ячейки, показана ниже для 15 шагов и еще ниже для 250 шагов. Изначально простое условие превращается в очень сложную схему, которую можно продолжать бесконечно. Откуда берется эта сложность? Подробности описаны в книге Стивена Вольфрама «Новый вид науки», изданной в 2002 году.

Алгоритмы дают новые возможности для создания миров с уровнем сложности, сравнимым с нашим. Алгоритмы, открытые в XX веке, заставили нас переосмыслить природу сложности. Революция нейронных сетей в 1980-х годах стала еще одной попыткой осмыслить всю сложность мозга, и хотя модели были значительно проще, чем биологические нейронные сети, разработанные нами алгоритмы обучения позволили исследовать общие принципы, такие как распределение информации в больших популяциях нейронов. Но как сложные функции сетей возникают из относительно простых правил обучения? Есть ли еще более простая система, проявляющая сложность, которую легче анализировать?

Клеточный автомат

Еще одна яркая фигура с серьезным научным подходом к сложности – Стивен Вольфрам (рис. 13.1), основавший Центр исследований сложных систем в Университете Иллинойса в 1986 году. Он был вундеркиндом, в 20 лет получил докторскую степень по физике в Калтехе, став самым молодым из тех, кому это удалось. Стивен решил, что нейронные сети слишком сложны, и стал исследовать клеточные автоматы.

У клеточных автоматов обычно лишь несколько дискретных значений, которые изменяются со временем в зависимости от состояния других клеток. Один из простейших клеточных автоматов – одномерный массив ячеек, каждая из которых имеет значение «0» или «1» (блок 7). Пожалуй, самый известный клеточный автомат – игра «Жизнь», которую в 1968 году изобрел Джон Конвей, Фоннеймановский профессор из Принстонского университета, и популяризировал Мартин Гарднер в своей колонке «Математические игры» в журнале Scientific American. Игра показана на рис. 13.2. Доска представляет собой двумерный массив ячеек, которые могут быть включены или выключены, и правило обновления зависит только от четырех ближайших соседей. При каждом шаге обновляются все состояния. В массиве генерируются сложные шаблоны, часть даже имеет имена – например, «планеры», которые пролетают через массив и сталкиваются с другими шаблонами. Начальные условия крайне важны для поиска конфигурации, отображающей сложные шаблоны.

Насколько распространены правила, создающие сложность? Стивен хотел узнать простейшее правило клеточных автоматов, которое может привести к сложному поведению, и поэтому начал перебирать их одно за другим. Правила под номерами от 0 до 29 создавали шаблоны, которые всегда возвращались к скучному поведению: в итоге все ячейки имели либо повторяющийся рисунок, либо фрактальный, с вложенными копиями самого себя. Однако правило 30 поражало непрерывно изменяющимися сложными моделями (блок 7). В конечном счете было доказано, что «правило 110» способно к универсальным вычислениям. То есть некоторые из простейших клеточных автоматов обладают возможностями машины Тьюринга, которая способна вычислить любую вычислимую функцию, поэтому она теоретически столь же мощна, как и любой компьютер.

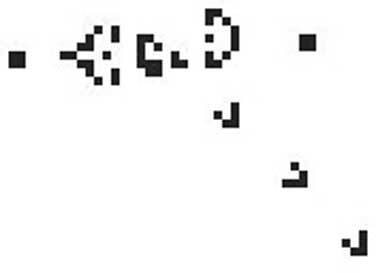
Рис. 13.2. Game of life. Снимок Планерного ружья Госпера (сверху), которое излучает последовательность «планеров», движущихся по диагонали, от «материнского корабля» сверху к правому нижнему углу

Одно из следствий этого открытия – вывод, что удивительная сложность, которую мы находим в природе, могла методом проб и ошибок развиться в простейшей среде химического взаимодействия между молекулами. То, что в ходе эволюции возникнут сложные комбинации молекул, ожидаемо и не должно считаться чудом. Однако клеточные автоматы – не достаточно хорошая модель зарождения жизни, и остается открытым вопрос, какие простые химические системы способны создавать сложные молекулы. Возможно, только особые биохимические системы обладают таким свойством, и это сужает вероятный набор взаимодействий, из которых могла возникнуть жизнь. Теперь мы знаем, что избыточность в мозге основана на разнообразии, а не на дублировании.

Важнейшее свойство жизни – способность клетки к самовоспроизведению. Джон фон Нейман из Института перспективных исследований в Принстоне прорабатывал этот вопрос в 1940-х годах с использованием клеточных автоматов. Фон Нейман – венгерский ученый, оказавший сильное влияние на многие области математики, включая его основополагающие работы по теории игр, упомянутые в главе 1. Какой простейший клеточный автомат может точно воспроизвести себя? Фон Нейман нашел очень сложный клеточный автомат с 29 внутренними состояниями и большим объемом памяти, позволяющим тому самовоспроизводиться. Это имеет определенный биологический интерес, так как у клеток с такой же способностью есть много внутренних состояний и память, выраженная в виде ДНК. С тех пор были найдены еще более простые клеточные автоматы, умеющие самовоспроизводиться.