Учим играть в нарды

Преимущество игр в том, что правила в них четко определены, а решения не столь сложны, как в реальном мире, но достаточно сложны, чтобы заставить людей соревноваться. В 1959 году Артур Самюэль, один из первопроходцев машинного обучения из компании IBM, написал программу, которая могла играть в шашки так хорошо, что в тот день, когда это было объявлено, акции IBM сильно подорожали. Шашки – относительно простая игра, но программа Самюэля оказалась впечатляющей для своего времени, учитывая, что он запустил ее на первом коммерческом компьютере IBM – IBM 701, – который работал еще на электронно-лучевых трубках. Программа была основана на функции стоимости, оценивающей сильные стороны различных игровых позиций, так же, как и предыдущие игровые программы, но ее отличало то, что она это освоила на собственном игровом опыте.

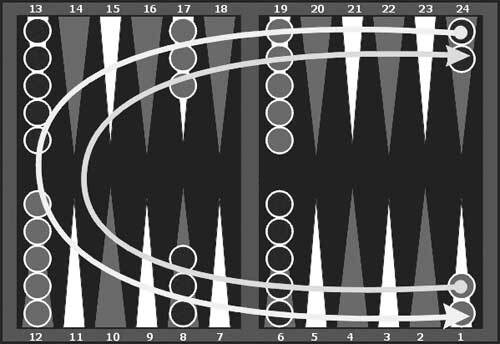
Рис. 10.1. Доска для игры в нарды. Нарды – это гонка до финиша, красные фишки движутся в направлении, противоположном направлению, в котором движутся черные (см. стрелки). Показана начальная позиция. Бросают два кубика, и числа на них указывают, на сколько шагов фишки передвигаются вперед

Джерри Тезауро перешел в исследовательский центр IBM имени Томаса Уотсона после того, как работал со мной над проблемой обучения нейронной сети игре в нарды. При обучения сетей с обратным распространением ошибки для оценки игровых позиций и возможных ходов мы использовали экспертный контроль (рис. 10.1). Недостаток такого подхода в том, что требуется много экспертных оценок позиций, и программа никогда не стала бы лучше наших специалистов, которые играли далеко не на уровне чемпионов мира. Но при игре с самой собой она могла бы добиться большего. Проблема игры с самой собой в том, что единственный обучающий сигнал – победа или поражение в конце партии. Но если одна сторона выиграла, то какой из многих ходов был решающим? Это называется временно́й задачей присваивания коэффициентов доверия.

Алгоритм обучения, который может решить временную задачу присваивания коэффициентов доверия, изобрел Ричард Саттон из Массачусетского университета в Амхерсте в 1988 году. Он тесно сотрудничал с Эндрю Барто, своим научным руководителем, в работе над сложными проблемами в обучении с подкреплением – отрасли машинного обучения, вдохновленной ассоциативным обучением в экспериментах на животных (рис. 10.2). В отличие от сети глубокого обучения, единственной задачей которой является преобразование входных данных в выходные, система усиления взаимодействует с окружающей средой в замкнутом цикле, получая входную сенсорную информацию, принимая решения и осуществляя действия, которые влияют на мир. Обучение с подкреплением основано на наблюдении за животными, которые решают сложные проблемы в изменчивой среде после того, как исследовали различные варианты и их результаты. По мере того как обучение улучшается, исследование уменьшается, что в конечном итоге приводит к чистому использованию лучшей стратегии, найденной во время обучения.

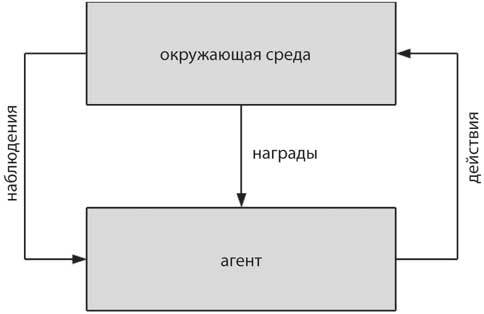
Рис. 10.2. Сценарий обучения с подкреплением. Агент активно исследует окружающую среду, предпринимая действия и делая наблюдения. Если действие выполнено успешно, агент получает вознаграждение. Цель в том, чтобы принять меры, которые максимизируют будущие выгоды

Предположим, вам нужно принять ряд решений для достижения цели. Если вы уже знаете все возможные варианты и ожидаемые будущие результаты, вы можете использовать поисковый алгоритм, чтобы выяснить набор вариантов, при котором выгода максимальна, но из-за этого размер задачи увеличивается по экспоненте – так называемое проклятие размерности. Но если у вас изначально нет всей информации о результатах выбора, вы должны научиться делать его по мере продвижения вперед. Это называется обучением в реальном времени.

Рис. 10.3. Ричард Саттон из Альбертского университета в Эдмонтоне в Канаде научил нас, как узнать путь к будущим наградам. Саттон перенес рак, но он остается лидером в обучении с подкреплением и продолжает разрабатывать инновационные алгоритмы. Он щедр на свое время и идеи, которые каждый в этой области очень ценит. Написанная им в соавторстве с Энди Барто книга «Обучение с подкреплением» стала классическим трудом

Алгоритм обучения в реальном времени, разработанный Ричардом Саттоном (рис. 10.3), зависел от различий между ожидаемым и полученным вознаграждением (блок 6). В обучении с учетом временной разницы вы сравниваете свою оценку предполагаемой долговременной награды за совершенный шаг в текущей позиции с лучшей, по статистике, оценкой награды, которую вы на самом деле получили, и предполагаемой награды после следующего шага. Если изменять предыдущую оценку так, чтобы она была ближе к улучшенной, решения, которые вы принимаете по мере продвижения, будут становиться все лучше и лучше. Изменения заставляют оценочную сеть учитывать будущее ожидаемое вознаграждение для каждой позиции на доске и использовать для принятия решения о следующем шаге. Алгоритм временной разности сходится к оптимальному правилу принятия решений в заданном состоянии после того, как у вас будет достаточно времени, чтобы изучить возможности.

Программа Джерри, названная TD-Gammon, знала важные особенности доски и правила игры, но не знала, что такое хороший ход. В начале обучения ходы были случайными, но в конце концов одна из сторон выигрывала и получала финальное вознаграждение. В нардах побеждает тот игрок, который первым «снимет» все фишки с игрового поля.

Блок 6. Обучение методом временной разницы

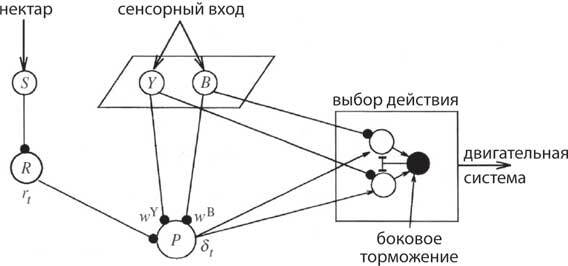
В этой модели мозга медоносной пчелы выбираются действия (например, приземлиться на цветок), которые максимизируют будущие награды:

R(t) = r_t+1 + γ r_t+2 + γ 2 r_t+3 + …,

где r_t+1 – вознаграждение в момент времени t+1, а 0 < γ < 1 – коэффициент обесценивания. Предсказанное будущее вознаграждение, основанное на текущих сенсорных входах s(t), вычисляется нейроном P:

P_t (s) = w^ys^y + w^bs^b,

где сенсорный ввод от желтых (Y) и синих (B) цветов взвешивается по w^y и w^b. Погрешность прогноза вознаграждения δ (t) в момент времени t определяется:

δ_t = r_t + _γ P_t(s_t) – P_t(s_t-1),

где r_t – текущее вознаграждение. Изменение каждого веса определяется:

δ w_t = αδ _t s_t-1,

где α – скорость обучения. Если вознаграждение больше, чем предсказанное вознаграждение, и δ_t положительна, вес увеличивается на сенсорном входе, который присутствовал до вознаграждения, но если вознаграждение меньше, чем ожидалось, а δ_t отрицательна, вес уменьшается.

Поскольку единственное реальное вознаграждение появляется в конце игры, логично ожидать, что программа TD-Gammon сначала изучит конец игры, затем середину и, наконец, ее начало. Это как раз то, что происходит в табличном обучении с подкреплением, где есть таблица значений для каждого состояния в пространстве состояний. Однако с нейронными сетями все иначе – они быстро хватаются за простые и надежные сигналы входных функций, а более сложные и сомнительные входные сигналы оставляют на потом. Первый принцип, который изучает TD-Gammon, – «выбрасывать фишки», придавая положительный вес входному элементу, который представляет собой количество снятых с доски фишек. Второй принцип – «блокировать фишки противника» – довольно эффективный способ практического решения проблемы на всех этапах, выученный путем присвоения положительного веса входному блоку, отмечающему количество заблокированных фишек противника. Третий принцип – «избегать блокировки» – естественная реакция на второй, и он изучается через придание отрицательного веса отдельным фишкам, которые могут быть заблокированы. Четвертому принципу – «занимать новые лунки», блокируя продвижение противника, – учат, назначая положительные веса уже занятым точкам. Для закрепления этих базовых принципов требуется несколько тысяч обучающих игр. За десять тысяч игр TD-Gammon изучила основные принципы. За сто тысяч – освоила продвинутый подход, а к миллиону игр ее методы достигли уровня чемпионов мира или вообще находились за пределами знаний людей начала 1990-х годов.

Когда в 1992 году TD-Gammon была представлена миру, она впечатлила и меня, и многих других. Функция стоимости представляла собой сеть обратного распространения ошибки с 80 скрытыми единицами. После 300 тысяч игр программа начала обыгрывать Джерри, поэтому он связался с известным игроком в нарды и автором книг о них Биллом Роберти и пригласил его посетить IBM, чтобы сыграть с TD-Gammon. Роберти выиграл в большинстве случаев, но, к своему удивлению, проиграл несколько хороших партий и заявил, что это лучшая программа для игры в нарды, с которой он когда-либо состязался. Некоторые из ее ходов были необычными, которые он никогда ранее не видел, и при ближайшем рассмотрении оказалось, что это улучшило игру человека. Роберти вернулся, когда программа сыграла сама с собой 1,5 миллиона партий, и был поражен, когда их встреча с TD-Gammon закончилась вничью. Программа стала настолько лучше, что, по его ощущениям, достигла уровня чемпионов. Специалист по нардам Кит Вулси заметил, что выбор «безопасной» (с низкими рисками и высокой вероятностью награды) или «смелой» (с высокими рисками и также большой вероятностью награды) стратегии игры у TD-Gammon лучше, чем у любого человека. Может показаться, что 1,5 миллиона обучающих игр – это очень много, но программа узнала из них лишь малую часть из ста квинтильонов (100 000 000 000 000 000 000) возможных позиций на доске, что требовало от TD-Gammon обобщения для новых позиций почти на каждом ходу.

TD-Gammon не получила такой широкой известности, как суперкомпьютер Deep Blue от IBM, который в 1997 году обыграл Гарри Каспарова в шахматы. Шахматы намного сложнее, а Каспаров в то время был чемпионом мира. Однако в некотором смысле TD-Gammon была более впечатляющим достижением. Во-первых, Deep Blue использовали специальное оборудование, чтобы просчитывать большее количество ходов, чем любой человек, побеждая «грубой силой». Для сравнения, TD-Gammon научилась играть, используя распознавание образов – стиль, более похожий на то, как играют люди. Во-вторых, TD-Gammon проявляла изобретательность и придумывала хитрые стратегии и позиционную игру, которые раньше никто не видел, и тем самым подняла уровень человеческой игры. Это достижение стало переломным в истории ИИ, потому что мы узнали что-то новое от программы, которая сама освоила сложную стратегию в хорошо изученной области, что достойно человеческого интереса и усилий.