На языке второго порядка можно написать такую систему аксиом, что наличие или отсутствие у неё модели будет равносильно соответственно подтверждению или опровержению континуум-гипотезы. А если соединить все эти аксиомы знаком конъюнкции, то возникнет формула второго порядка, которая тогда и только тогда имеет модель, когда континуум-гипотеза справедлива; такая формула и была обещана в главе 4, в конце четвёртого размышления. Указанную систему аксиом мы и намерены выписать в настоящем приложении.

Пусть множество M обладает следующими свойствами: 1) его мощность континуальна; 2) в нём выделено некоторое такое подмножество Q счётно-бесконечной мощности, что всякое подмножество множества, содержащее, в свою очередь, Q в качестве подмножества, имеет мощность либо счётно-бесконечную, либо континуальную. Легко проверить, что возможность такого множества равносильна подтверждению континуум-гипотезы. Поэтому всякое такое M временно условимся называть подтверждающим. Наша цель – выписать систему аксиом, задающую подтверждающее множество. Для этого мы воспользуемся следующей теоремой из теории упорядоченных множеств: всякое линейно упорядоченное множество, обладающее плотным в нём счётно-бесконечным подмножеством и такое, что любое его сечение дедекиндово, имеет мощность континуума. (Напомним, что сечением линейно упорядоченного множества называется такое его разбиение на два класса, нижний и верхний, что любой элемент нижнего класса предшествует любому элементу верхнего класса. Сечение называется дедекиндовым, если либо в нижнем классе есть наибольший элемент, либо в верхнем классе есть наименьший элемент, но не то и другое вместе.) Система аксиом, которую мы собираемся выписать, как раз и задаст нам в качестве подтверждающего такое линейно упорядоченное множество, причём в роли Q выступит подмножество, плотное в M. (Подмножество A упорядоченного множества B называется плотным в B, коль скоро для любых двух различных элементов из B найдётся элемент из A, расположенный между ними.)

Но прежде чем выписывать аксиомы, необходимо указать сигнатуру. Наша сигнатура имеет четыре члена. Она состоит из константы «0Q», имени «Q» одноместного отношения (т. е. свойства), имени двуместного отношения и имени «'» одноместной операции. Об этих членах сигнатуры не требуется знать ничего, кроме того, что будет записано в аксиомах.

Как известно, носителем модели называется множество её элементов. Все операции и отношения модели считаются заданными на её носителе.

Начнём выписывать аксиомы, попутно их комментируя.

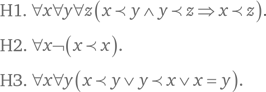
Аксиомы H1–H3 утверждают, что отношение представляет собою строгий линейный порядок, определённый на носителе модели. Таким образом, этот носитель оказывается линейно упорядоченным множеством.

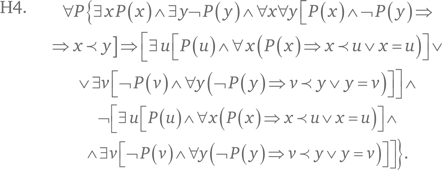
Аксиома H4 утверждает, что линейный порядок на носителе является дедекиндовым. (Сечение образуется областями истинности свойств P и ¬P.)

Аксиома H5 утверждает, что между любыми двумя элементами носителя найдётся элемент из области истинности свойства Q (т. е. из множества тех элементов носителя модели, которые обладают этим свойством). Иначе говоря, аксиома утверждает, что эта область плотна в носителе.

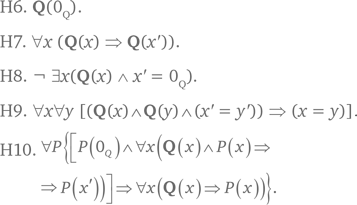
Аксиомы H6–H10 гарантируют счётную бесконечность области истинности свойства Q. В самом деле, аксиомы H6 и H7 означают, что элемент 0Q принадлежит области истинности свойства Q, а операция «'» не выводит за пределы этой области. Аксиомы H8 – H10 напоминают аксиомы Пеано I–III; их можно было бы назвать «аксиомами Пеано» для области истинности свойства Q. Эта область истинности, следовательно, представляет собою один из натуральных рядов (со строчной буквы, разумеется). Поэтому она, эта область, счётно-бесконечна.

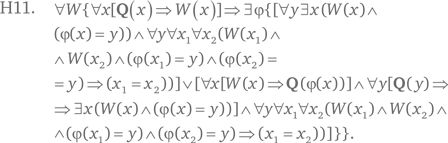
Аксиома Н11 (последняя) утверждает нечто о произвольном надмножестве области истинности свойства Q; в аксиоме это надмножество фигурирует в качестве области истинности свойства W. А именно: H11 утверждает, что всякое такое надмножество находится во взаимно однозначном соответствии либо с носителем модели, либо с областью истинности свойства Q. В первом случае оно континуально, во втором – счётно-бесконечно. Соответствие, о котором идёт речь, представлено функцией φ, которая взаимно однозначно отображает область истинности свойства W либо на весь носитель, либо на область истинности свойства Q.